单路径导引的车式移动机器人协同编队控制

王常顺 王 丹 彭周华

(1.大连海事大学船舶电气工程学院,辽宁大连 116000;2.山东交通学院信息科学与电气工程学院,山东济南 250357)

1 引言

在沥青路面就地热再生养护中,通常由2–4台加热机和铣刨机编组后沿施工车道列队低速行驶以满足施工的工艺需求[1].限于沥青的粘度特性,加热后的路面温度高达160◦C.为减少施工人员在恶劣高温环境下的工作时间,降低人力成本,提高施工质量和经济效益,研究就地热再生机组协同控制系统来实现机组列队自动驾驶具有重要的应用价值.编组中各工程车辆均采用前轮转向,后轮驱动的底盘结构,可视为车式移动机器人[2].

轨迹跟踪[2–8]是移动机器人集群控制[9–19]的基础,得到了很多研究者的关注.例如,文献[3]基于滑模控制算法设计了直流电机驱动的CLMRs路径跟踪控制器,实现了曲线轨迹跟踪.文献[4]设计的滑模轨迹跟踪控制器实现了精准的并行倒车.但滑模控制中的高频抖振会给液压式转向机构带来严重的磨损.文献[5]基于神经网络设计了模型预测控制器,实现了包含不确定性参数的移动机器人的轨迹跟踪控制.但受限于精准的数学模型和复杂的计算量,工程实现上具备一定的难度.文献[6–7]利用LESO将系统未建模动态和模型不确定性当作外部扰动进行补偿,设计了移动机器人轨迹跟踪自抗扰控制器,便于工程实现,但未展开针对CLMRs编队控制的研究.

移动机器人的编队控制研究中,常采用领航–跟随法[8–12,17–22]、虚拟结构法[13–14]和基于行为法[15]等策略.文献[8]基于交通流理论提出了一种汽车队列纵向鲁棒控制器,但其横向控制精度无法达到施工要求.文献[9]通过跟踪期望速度和角速度,实现两台移动机器人运动中保持相对固定的间距和角度.文献[11]进一步实现了4台移动机器人在操场形状轨迹上的编队控制,但曲线路径的跟踪性能和队形保持的精度无法令人满意.为更好保持队形,文献[16–18]将编队控制问题转换为轨迹跟踪问题,根据各车式移动机器人在编队中的位置,单独计算出轨迹参数,在运动学层面上实现了CLMRs编队控制,但没有进行运动学协同和动力学控制相关的研究.文献[19]利用RBF神经网络逼近并补偿CLMRs系统模型的非线性部分和未知扰动,通过多路径导引实现了固定队形控制.文献[15,20]中的分布式编队控制器同样仅适用于多条路径导引的固定队形控制.然而受施工道路未知曲率的影响,弯道上的机组集群队形难以准确描述队形.另一方面因天气等外部因素,施工中会不断调整领航车速和车间距,上述方法需不断计算并更新跟随机器人的轨迹参数,增加了系统的计算负担,甚至引起不稳定,降低了系统的实用性.

本文针对施工背景下的CLMRs集群,首先在运动学层级设计了分布式协同编队制导律,通过单条参数化路径导引CLMRs列队行驶,减轻路径参数更新引起的计算和通信负担,规避了负速度;然后在动力学层级基于LESO设计了带有外部扰动补偿的CLMRs前向速度和姿态角控制器,降低速度超调和转向操纵频率,提高了横向控制精度;最后通过级联系统稳定性理论分析了闭环系统的稳定性,并通过数字仿真和加热机群实验结果验证了控制器的有效性.

2 问题描述

2.1 CLMRs数学模型

为实现编组中工程车辆沿施工路线以队列形式自动驾驶,本文研究的车式移动机器人采用图1所示的阿克曼结构,通过后轮提供前进动力,通过操纵前轮控制行进方向.在一个由N台车式移动机器人和M个虚拟领导者组成的系统中,第i个车式移动机器人的运动学模型[2–3]可表示为

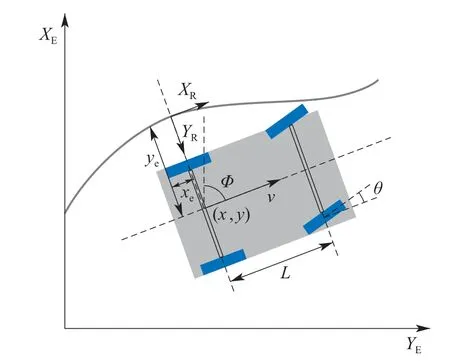
图1 车式移动机器人示意图Fig.1 Structure of CLMRs

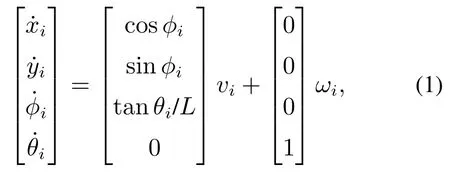
式中:pi=(xi yi)T表示CLMRs在固定坐标系XEYE下的位置,φi表示车体的姿态角,θi表示前轮的方向角,L表示后轮到前轮的轴距,qi=(vi ωi)T是载体坐标系下机器人的行进速度和前轮侧转角速度.

与差速式移动机器人不同,CLMRs的转向角速度与前向速度有关,也无法实现原地转向.运动过程中所受的非完整约束可表示为

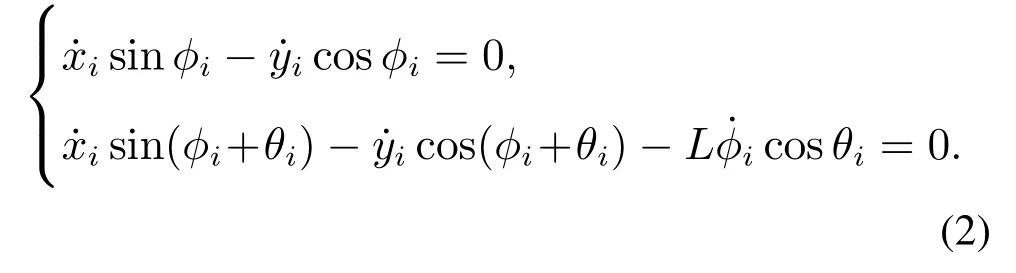
CLMRs运动主要受纵向牵引力及转向力控制,考虑到实际运行中前轮方向角通常比较小,其动力学模型[2,10]可表示为

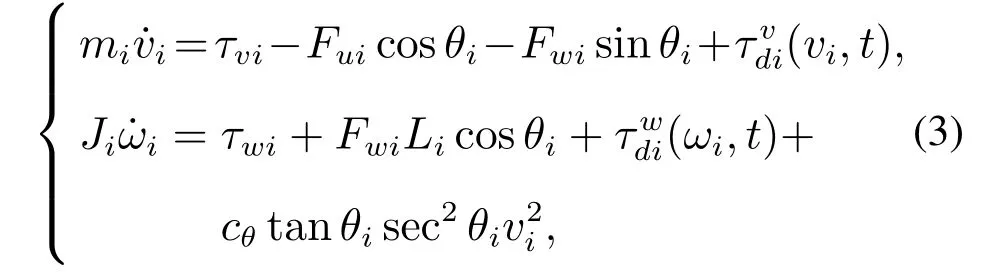
式中:τvi为牵引力,τwi为施加在转向轮上的力矩,Fui为前进方向所受的摩擦力,Fwi为横向受力,和为其他摩擦力与外部干扰之和,Ji,Jb,Jv,Jh为系统中不确定的惯性系数,与CLMRs参数有关,r为车轮半径,cθ=(mi+Jb+4Jv)/L2+Jh/r2.

2.2 路径生成方法

本研究中通过虚拟领导者引导CLMRs沿期望路径运动,所需参数化路径[21–22]至少是二阶连续的.在实际应用中可以采用最小二乘法或样条插值对路径曲线进行拟合,进而生成该参数化路径.对于期望路径上的任意点,用prk=(xk(δ)yk(δ))T表示其位置,用表示其姿态角,其中:δ是与时间独立的变量,

为了实现虚拟领导者和CLMRs的协同运动,将虚拟领航者路径参数的导数设计为

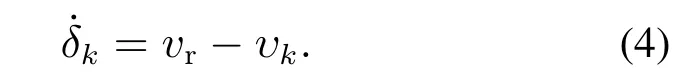
综上分析,可将CLMRs的轨迹跟踪误差[19]记为

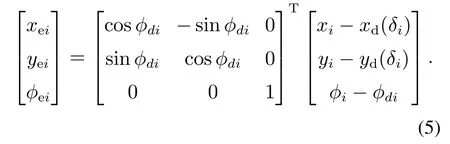
联立式(1),可得到轨迹跟踪误差动态为

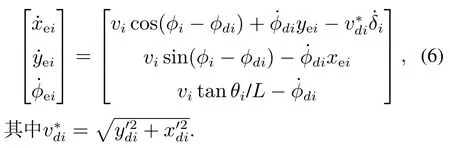
2.3 控制目标

本文的控制目标为:考虑由式(1)和式(3)表示的CLMRs集群,通过设计协同路径跟随控制律和使得每个车式机器人都能以设定间距pdij和设定速度vr跟随给定的参数化路径,且误差收敛至零点附近的有界临域内,也即存在任意小的正常数,满足:

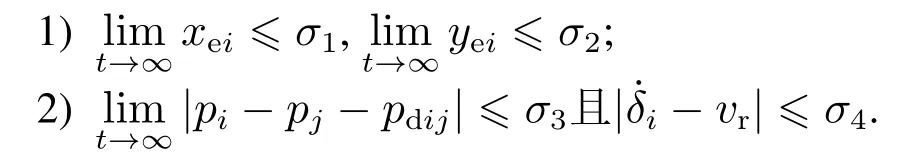
3 控制器设计

本节将从运动学和动力学两个层面设计车式移动机器人的协同编队控制器,图2为所设计的编队控制器组成结构.

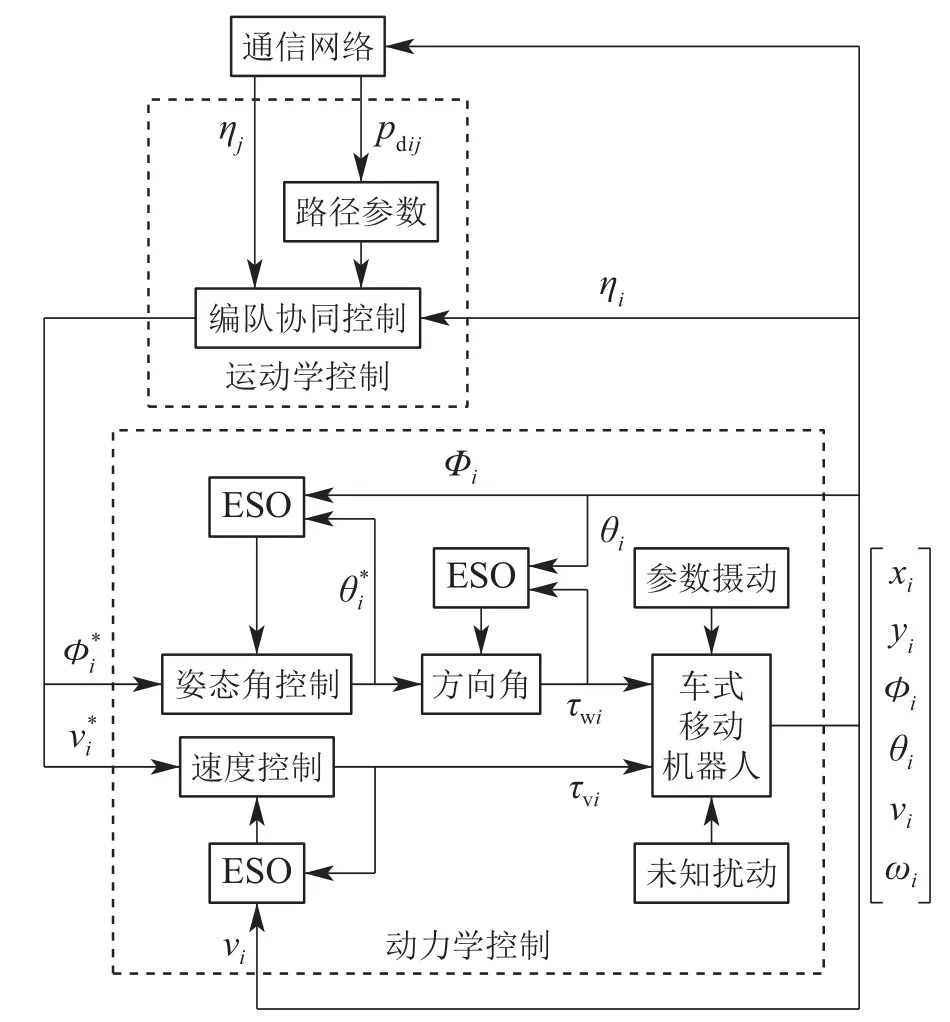
图2 编队控制器组成结构Fig.2 Structure of formation controller

3.1 运动学控制器设计

假设1每个车式移动机器人与虚拟领航者之间都能进行有向通信,并获取临近机器人的运动状态信息.

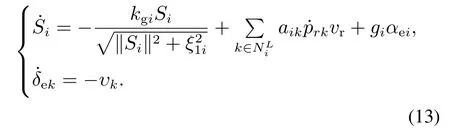
3.2 动力学控制器设计

在第3.1节中,为集群中的车式移动机器人设计了期望前向速度和姿态角.本节中将设计CLMRs的动力学控制器,使得实际前进速度和姿态角可以满足运动学控制器的要求.但在实际工程应用中,由于工况改变以及运动中会受到外部干扰等因素影响,模型中部分参数会产生摄动,造成CLMRs模型中参数难以精确辨识.将式(3)中CLMRs的动力学模型重写为

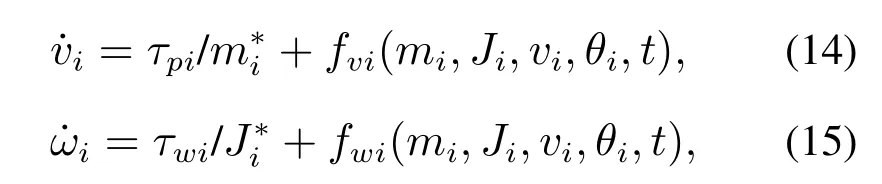
借鉴自抗扰控制器中利用ESO估计被控对象外部扰动的方法[6–7],文中基于LESO分别设计了前向速度和姿态角控制器.

3.2.1 前向速度控制器

对式(14)所示的前向速度控制系统,设计二阶的LESO为

式中:kvi为系统控制增益,ξ2i为正常数.

3.2.2 姿态角控制器

联立式(1)和式(15),可得CLMRs的姿态角控制系统

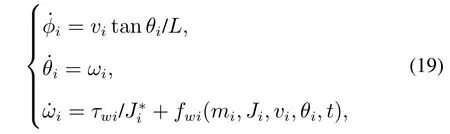
由式(19)可知,姿态角控制系统不是单纯的积分串联系统,下面将结合反步法思想完成控制器设计.

首先,引入虚拟控制量uφi=vitanθi/L,为姿态角控制系统设计二阶LESO如下:

式中:kφi为控制增益,ξ3i为正常数.

注1实际系统中考虑到CLMRs执行部件的输出连续且功率有限,而因外在环境引起的系统扰动能量也有限,因此,fvi,fwi和均连续有界且可导,即假设2是合理的.

4 稳定性分析

本节将逐步分析LESO子系统、动力学子系统、运动学子系统的稳定性,最后分析文中所设计的闭环系统稳定性.

4.1 LESO子系统稳定性

因为A1i,A2i,A3i都是Hurwitz矩阵,所以存在正定矩阵P1i,P2i和P3i使不等式(31)–(33)成立

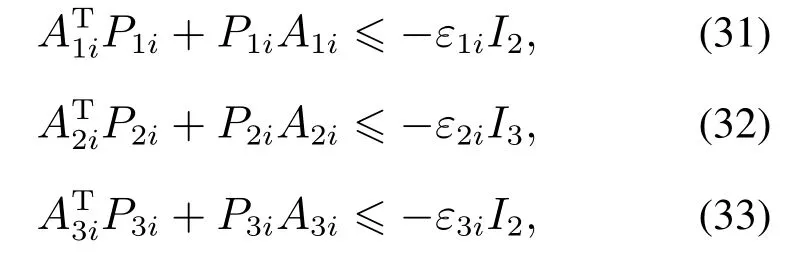
式中:ε1i,ε2i,ε3i都是正数,I2和I3分别表示2×2和3×3单位矩阵.

定理1在满足假设2的前提下,式(28)所示的LESO前向速度控制子系统:是输入到状态稳定(input-to-state stable,ISS)的.

证针对式(28)所示的子系统,选取如下Lyapunov方程

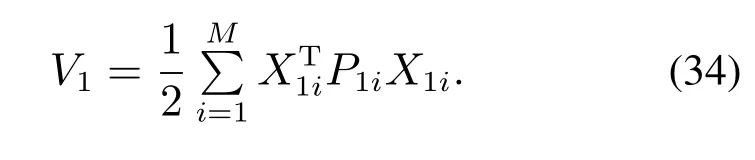
对式(34)求导,可得

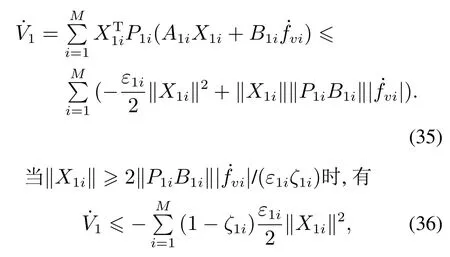
式中ζ1i ∈(0,1).根据文献[23]中的定理4.6可知,式(28)所示的LESO子系统是ISS的,且存在

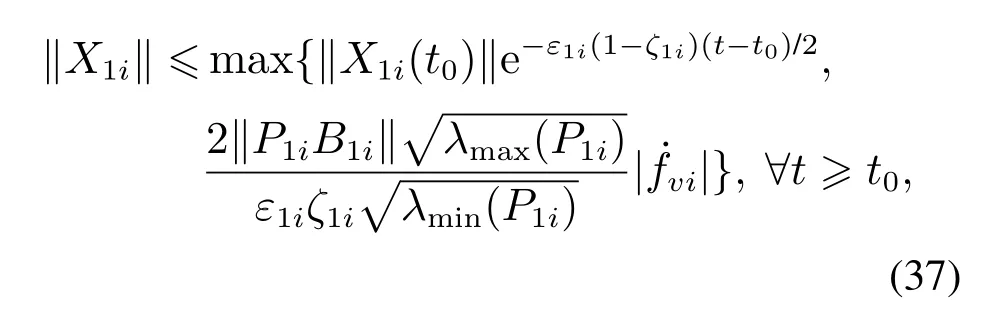
式中:λmax(·)和λmin(·)分别表示矩阵的最大特征值和最小特征值,t0表示初始时间. 证毕.

因式(29)和式(30)所示LESO子系统的证明过程与定理1类似,在此不再一一赘述.

定理2在满足假设2的前提下,式(29)所示的LESO转向角控制子系统是ISS的,且估计误差的边界为

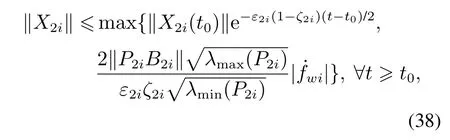
式中ζ2i ∈(0,1).

定理3在满足假设2的前提下,式(30)所示的LESO姿态控制子系统是ISS的,且估计误差的边界为

式中ζ3i ∈(0,1).

4.2 动力学子系统稳定性

因运动学中的速度跟踪误差和姿态跟踪误差是有界的,可知动力学跟踪误差也是有界的. 证毕.

4.3 运动学系统稳定性分析

4.4 级联系统稳定性分析

定理1–5分别证明了闭环系统中各个子系统的稳定性,接下来将分析由这些子系统级联的CLMRs协同编队闭环系统的稳定性.

定理6考虑由多个车式移动机器人构成的分布式协同编队系统,其中,式(1)和式(3)分别表述了其运动学和动力学方程,式(11)表述了其运动学控制律,式(12)表述了其路径更新律,式(16)和式(19)表述了基于LESO 的动力学控制器.若假设1 和2 满足,则CLMRs协同编队闭环控制系统是ISS的.

证根据定理1–5,由式(17)(21)(24)和式(26)中的子系统组成的级联系统是ISS的,且当t →∞时,有

式(50)表明,闭环系统中所有信号都是一致最终有界的. 证毕.

5 试验验证与结果分析

本节对4台如图1所示的车式移动机器人集群进行协同编队试验测试,其通信拓扑结构如图3所示,分别通过仿真试验和4台工程车辆编队测试来验证所设计控制器的有效性和控制性能.

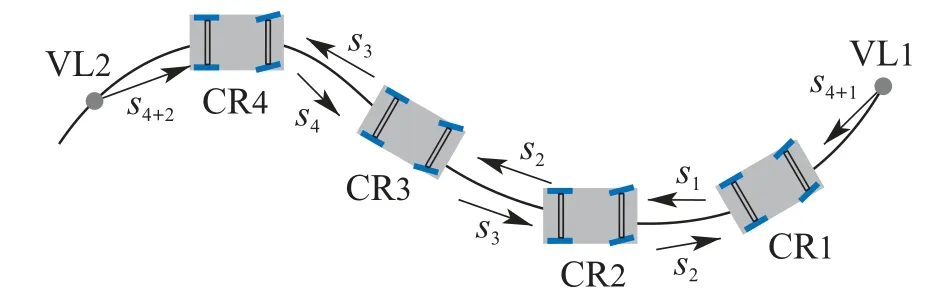
图3 通讯拓扑结构Fig.3 Communication topology

5.1 仿真测试

考虑由虚拟领航者和CR1–CR4组成的CLMRs集群,仿真中CLMRs选取的物理参数[19]如表1所示.给定虚拟领航者的期望速度vd=1.7 m/s,期望队列间距pij=34 m.为验证CLMRs集群形成期望队列并沿期望路径运动的性能,初始状态时,将CLMRs随机分布在期望路径的两侧,且因回转半径较大,仿真中设定CLMRs的初始方向与起始路径点夹角不超过90◦,初始值如表2所示.

表1 CLMRs参数Table 1 CLMRs parameters

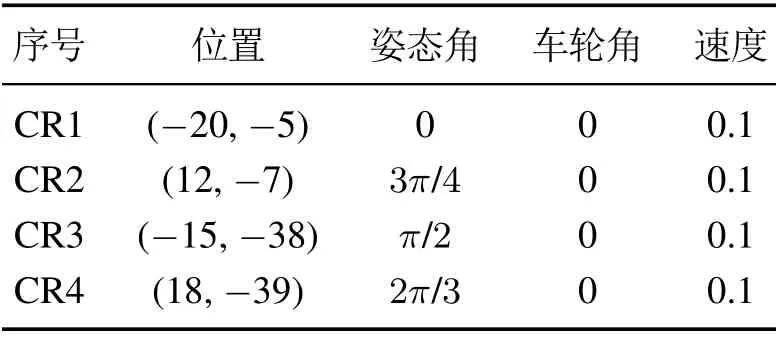
表2 仿真中CLMRs的初始状态Table 2 Initial states of CLMRs in simulation

为了进一步验证本文控制器的效果,参照文献[19]中的神经网络PID算法进行了仿真对比试验,得到的仿真结果如图4–7所示.图中分别展示了协同编队的CLMRs运动轨迹、姿态角、前向速度及转向轮的偏转角度.

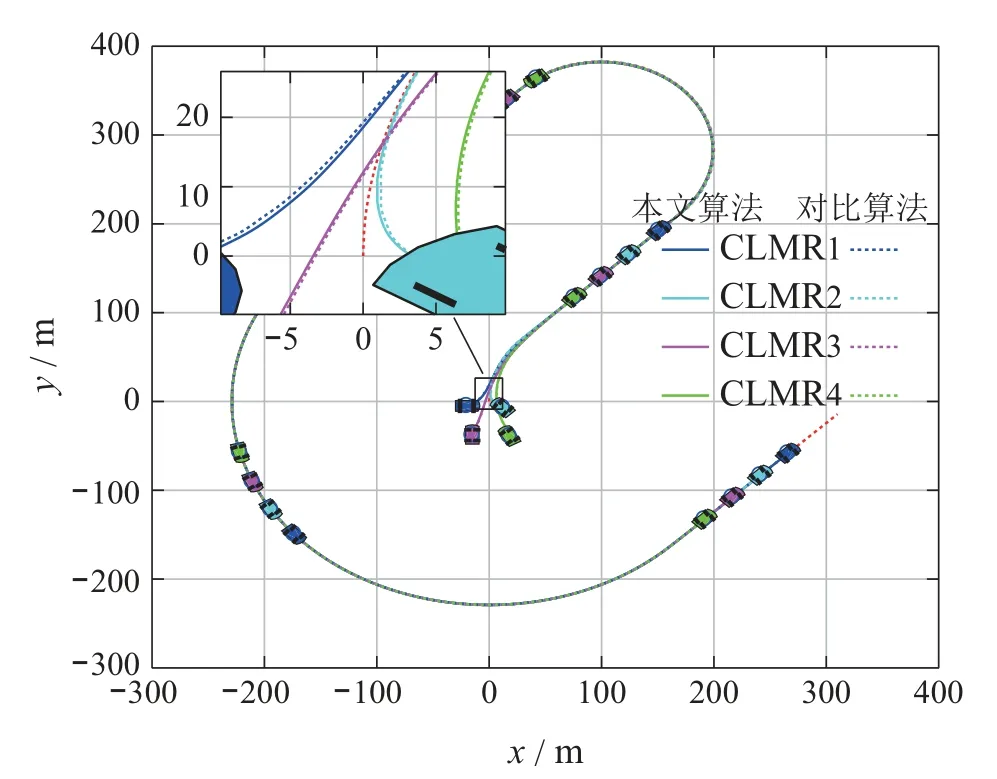
图4 CLMRs路径跟随性能Fig.4 Path following performance

从图中可以看出,CLMRs能够按期望的等间距队形跟踪期望路径,跟踪误差小,前进速度稳定,姿态角及车轮方向角变化平稳,无振荡现象,说明所设计控制器实现了CLMRs协同编队控制,且对系统参数摄动和外部扰动具备很好的抑制作用.相对于文献[19]中的控制方法,本文控制器可以有效地减小速度冲击和姿态角振荡的幅度,降低操纵转向的幅度和频率,具有明显的工程应用优势.

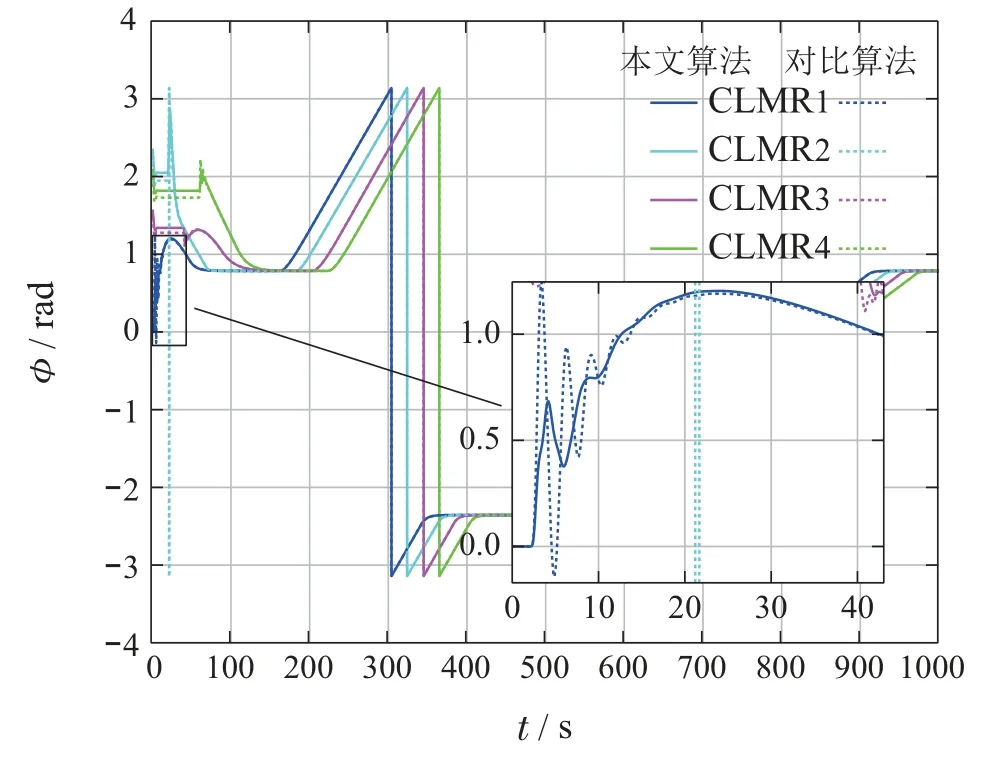
图5 姿态角Fig.5 Attitude angle

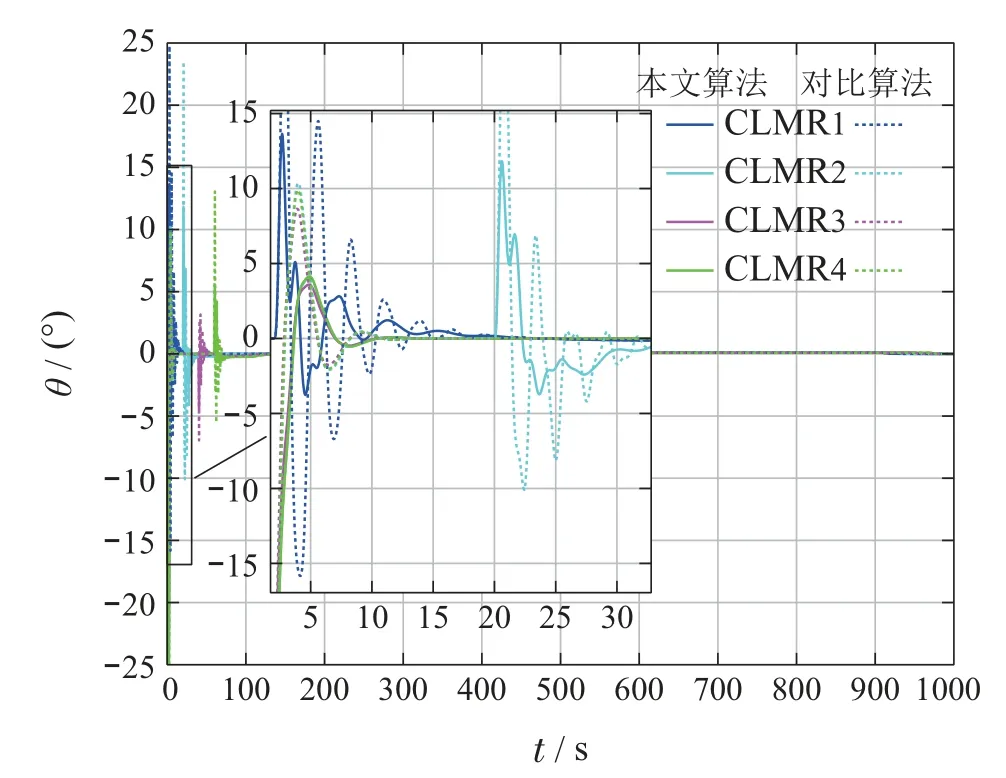
图6 前向运动速度Fig.6 Forward velocity

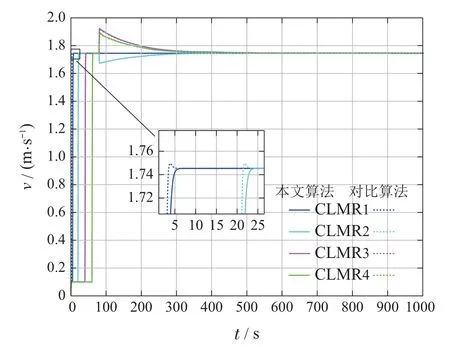
图7 转向车轮角度Fig.7 Steering wheel angle

5.2 现场实车测试

为进一步测试该控制器的性能,将所设计的控制器应用到与山东省路桥集团公司合作研发的就地热再生加热机组智能驾驶系统中.控制目标是让4台加热机编队沿施工路线自动行驶,行驶速度稳定,横向偏差不大于50 mm.该套机组底盘采用后轮驱动和前轮转向的阿克曼结构,前进液压马达和转向液压缸通过比例阀控制,从而实现前进速度和前轮角度的控制.

图8 就地热再生加热机群Fig.8 Hot-in-place preheater vehicles

该系统中单车设计重量mi ≈18000 kg,轴距Li=13.75 m.施工前首先通过最小二乘法和样条插值方法对施工车道进行拟合处理,得到一组以施工起始点为原点的连续光滑参数路径.机组通过RTK–DGPS和INS提供组合定位信息,然后进行高斯投影运算,可得到精度±10 mm的定位信息.因对机组加热装置预热时不能原地停留,通常人工驾驶机组进入施工路段后再开始自动驾驶,此时已形成队列且横向偏差小于200 mm,但纵向偏差较大.随着施工的进行,路面曲率和坡度不断变化,需要所设计的控制器能够通过操纵方向盘和比例阀,控制加热机组以设定间距的队列沿施工路径无偏差自动驾驶.实验测试在济南遥墙机场附近的青银高速西向东路面养护施工中展开,经采集后得到的实验路段参数路径为:y=0.00096x3+0.006x2−0.26775x −0.015841.

图9中展示了施工中加热机组的行驶轨迹,图10展示了各车的横向路径跟踪偏差及纵向距离偏差.从图中可以看出,该系统实现了4台加热机组的协同编队控制,行驶速度稳定,控制精度符合预期目标.

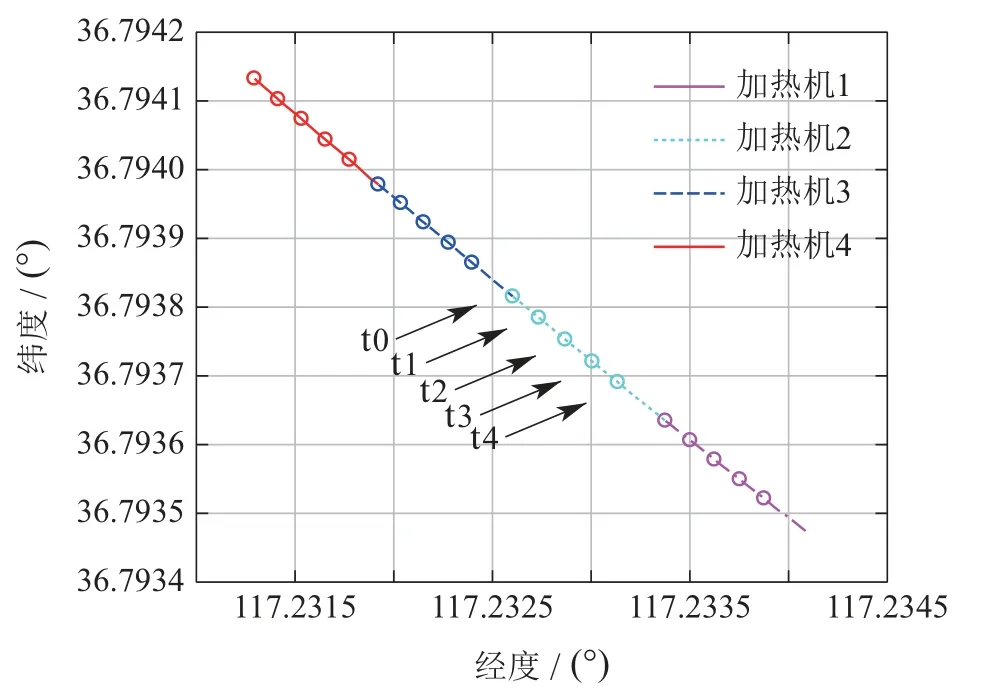
图9 机组定位信息Fig.9 Position information of vehicles

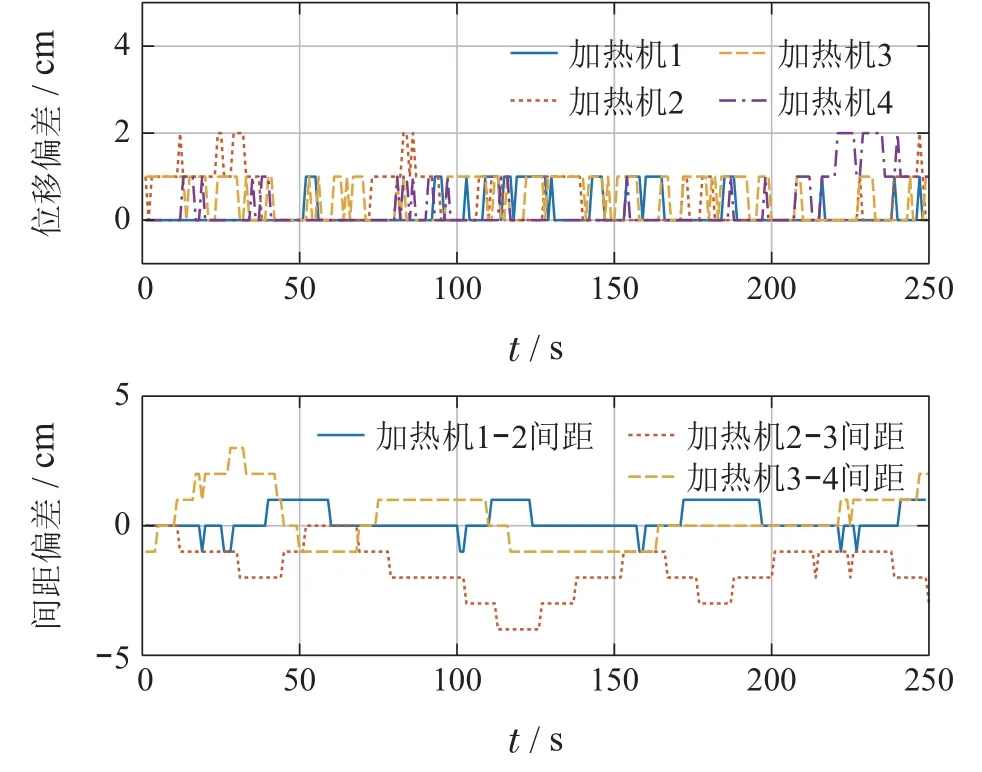
图10 机组跟踪误差Fig.10 Tracking errors of vehicles

6 结论

本文针对含有模型不确定性和未知外部扰动的车式移动机器人集群编队控制问题进行研究,首先设计了分布式协同编队制导律和基于LESO的前进速度及姿态控制律,实现了单路径引导下的CLMRs协同编队控制,然后利用级联系统稳定性理论分析了闭环系统稳定性,最后通过数字仿真和加热机群实验结果验证了控制器的有效性.