孤岛交流微网群中各微电网分布式有功–电压调控策略

张 博 窦春霞 岳 东 张占强张腾飞

(1.燕山大学电气工程学院,河北秦皇岛 066004;2.南京邮电大学先进技术研究院,江苏南京 210023;3.南京邮电大学自动化学院、人工智能学院,江苏南京 210023;4.岭南大学电气工程系,庆山庆尚北道38541,韩国)

1 引言

偏远地区或者重要的岛屿由于地域原因,很难得到大电网的供电支撑,因此目前供电方式灵活实用的分布式电源(distributed energy resource,DER)得到了众多学者青睐,并被用于维持这些地区的正常供电.而为了让多个DER共同为负载稳定供电,目前已经研发出了由储能设备、DER、控制环和负载组成的“微电网”(microgrid,MG)[1–2].但单个MG的供电也是有限的,因此常将多个MG连接起来,形成一个“微电网群”(microgrid cluster,MGC),共同为负载供电.并且,随着通信技术的发展,MGC中的MG都是互联通信的.这样,多类通信数据就可以被整合处理成控制指令,以调控物理系统的运行.即,MGC是一个典型的信息物理融合系统[3–5].

而在该类信息物理融合系统中,实现各MG的电压稳定和有功功率的合理分配[6–7],就是本文的两个研究目标.其中,电压稳定是指由于群中的多个MG是经过电压源变流器(voltage source converter,VSC)和母线连接在一起的,因此就要使得每个MG中VSC输出的电压一致并等于母线电压.这样,每个MG内部的DER也要进行对应的调控[8–9].而功率合理分配则包含两层意思,即每个MG的出功都应该被合理规划,以维持公共负载的需求;每个MG内部的DER与储能设备也应该被合理出功,以使得运行成本最低.

目前,对于MGC的电压稳定问题,已有学者进行了相关研究:为了在系统故障时还能维持MGC中公共母线电压的稳定,文献[10–11]设计了自适应下垂控制结构.但采用该类控制,不能避免DER输出的电压或者频率值都与参考值存在偏差:文献[12]根据多MG联络线功率指令设计了MGC系统串并联不同结构的两级分层控制,通过中央控制器进行协调控制.但是该类集中式的控制策略容易出现单点故障问题;文献[13]基于优化的思想,提出了MGC的分层控制策略,以应对不同的功率供需情况与外界运行环境.但是,该类控制策略并没有分析所设计的控制器是否会对原系统的稳定运行造成影响.

针对MGC的功率分配问题,目前的研究被分为两大类型:1)采用能量管理策略,通过设计目标函数和限制条件来计算出MG中各机组的最优出力;2)采用一致性算法来调节MG中各机组的边际成本,进而计算出最优出力.对于类型1而言,文献[14]针对并网MGC中功率波动的问题,提出了衡量波动性的熵值优化函数来优化各机组的出功;文献[15]提出了考虑通信故障情况下的MGC多级管理策略;文献[16]设计了不同时间尺度下MGC的分层能量管理策略;文献[17]在MGC的功率调控中考虑了要最大化延长储能设备的使用寿命,并基于模型预测控制设计了相应的能量管理策略.对于类型2而言,文献[18]运用多智能体一致性理论提出了孤岛MGC实时协同功率分配的框架;文献[19]考虑了MGC中的线路损耗,提出了计及线损的一致性调控策略来调节出功;文献[20]提出了一种基于储能设备分层控制的MGC功率分配方法;基于稀疏通信网络,文献[21]将牛顿法和一致性算法结合,设计了MGC的分布式优化调度策略;文献[22]提出了一种基于交替乘子法,模型预测控制和一致性算法的MGC优化调度策略;文献[23]将MGC的发电成本看为一个与发电量相关的二次函数,并由交替乘子法求解各MG的最优发电量.

基于对上述文献[14–17]的分析,发现存在如下问题:能量管理策略的最小时间尺度是分钟级别,但MG的控制系统对于响应时间的要求是毫秒级别,时间尺度上并不匹配.而分析文献[18–23],发现大多的边际成本都是基于一致性算法来调节的.但是,一致性算法的完成也是需要基于稀疏网络通信的,即会增加通信成本.并且,算法的实现也是需要时间的,这样实时性上就难达到MGC系统的要求.

针对上述文献存在的问题,为使得每个MG都能保持电压稳定并且承担合适的负载需求以降低发电成本,本文的主要工作如下:

1) 电压调控:在MG之间,为每个MG的VSC都设计了控制目标;在MG内部上,对每个发电设备都设计了反下垂控制器和二次控制器(基于数据通信,生成并添加电压调节量),来调控电压至最优值;

2) 对于有功功率分配而言:在MG之间,为降低各机组的发电成本,规划了有功功率分配目标,计算出每个MG应该承担的负载需求;在MG内部,根据其应该承担的负载需求,设计了一种基于边际成本一致与电流调控的功率分配策略,完成了对每个DER与储能设备的出功调节,并不会增加通信成本.即便系统中的公共负载出现扰动时,该策略也能有效地调节各DER与储能设备的出功;

3) 稳定性分析:在完成电压和有功功率的调控后,本文构建了相应的小信号模型,以分析提出的调控策略对于DER自身控制环路的影响.

相比于以往的文献,所提方法有效实现了MGC的分布式调控,减轻了通信负担,弥补了当前调控策略的缺乏,实现了各发电设备输出电压的同步调控和快速有功功率分配.

2 控制架构

2.1 设计整体控制架构

本文所设计的控制架构被分为两层,即MG间的控制层和MG内部的控制层.其中,MG间的控制就是指各个MG间如何有效地调控,以使得整个交流MGC维持电压稳定和功率均分;MG内部的控制就是指单一MG内部各发电设备也要满足输出电压稳定并且合理出功,以满足各MG的出功目标.

本文提出的控制架构如图1所示.在该图中,MGC包括多个MG、通信网络、负载、VSC、VSC控制系统和公共负载等;MG包括DER、通信网络、二次控制器、储能设备、线路阻抗、电流调控环节、控制环、本地负荷等.每个环节之间的运行关系如下:首先,各DER将在逆变器控制环路的调节下输出电压和电流至本地负载和MG母线,再经过VSC来给公共负载供电.同时,每个DER的输出电压也会经由上传信道输送至一致性算法中,进而完成电压二次控制.一旦系统中发生了负载扰动,就需要先计算出每个VSC对应的电压调节量和功率调节量,然后分别基于一致性算法和边际成本一致准则来设计每个MG中DER的电压调节量和有功调节量.一旦MG中出现发电设备出功达到限值的情况,就要重新规划发电设备的最优出功;其次,调节后的电压量将被添加至电压合成环节,与下垂控制输出的频率一起被合成为一个电压矢量,并被送入双闭环中,得到一个脉冲宽度调制(pulse width modulation,PWM)触发信号;最后,得到的PWM信号将被用于调节逆变器的通断,进而重新调控电源的输出电压和电流.

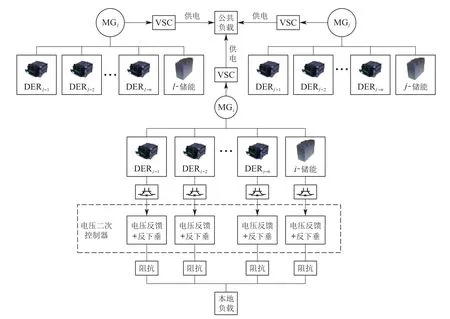
图1 MGC的控制结构Fig.1 The control structure of MGC

图1中各部分的作用如下:

1) DER控制层:a)稳定性分析;b)设计电压二次控制器及反下垂控制器;c)设计电流调控环节;

2) 微电网内控制层:基于边际成本一致,计算各发电设备要承担的有功功率;

3) 微电网间控制层:a)构建优化控制目标;b)计算最优输出电压值;c)计算有功功率调控值.

MGC的通信架构如图2所示,可以被分为两层网络,即MG之间的通信网络和MG内部各电源的通信网络.其中,MG之间网络的通信数据为各自VSC控制输出的电压值和电流值,而在该通信网络的计算终端可以得到各MG应当输出的最优电压值和承担的负载供电量;MG内部网络的通信数据为各电源的输出电压和边际成本,而在该网络的计算终端可以得到各电源的电压和有功功率调控指令.基于这些指令,就可以完成相应的电压二次控制,电流调控和有功功率调控.在图1和图2中,“DERj−1”和“j-储能”分别代表第j个MG中的第1个DER和储能设备,两图中其他符号的含义也类似.

图2 MGC的通信架构Fig.2 The communication structure of MGC

2.2 设计整体控制架构

在MGC中,各MG都是通过VSC连接到公共母线上给公共负载供电的.因此,在MG之间都是基于VSC来完成电压和有功功率调控的.在MGC中,对于并联供电的多个MG而言,维持电压稳定和有功功率按照VSC的调节能力进行分配(调节能力越大,需要提供的有功功率越小)是两个基本控制目标.因此,设计合适的调控手段,以实现MG之间根据本身VSC对应容量比例系数均分各自需要提供的有功功率就很有必要.

首先,给出电压稳定和有功功率均分的目标如下:

1) 电压稳定.

对于电压而言,各MG中VSC的输出值需要达到如下调控目标.

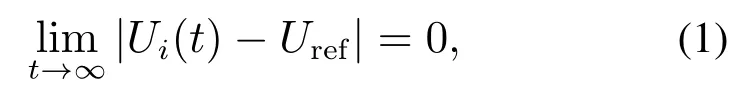
其中:Ui(t)代表第i个MG 对应VSC输出的电压值;Uref代表电压参考值,一般为公共母线电压值;代表当时间趋于无穷时求极限值.各MG的VSC对应的电压参考值应该是一致的,否则会产生环流.

2) 有功功率均分.

在本文中,各MG的VSC都是运行于下垂控制模式下的,并且考虑到每个VSC输出的电压都应与母线电压一致,因此借鉴文献[24]中的研究,得到MGC内有功功率均分的条件如下(假设MGC中共有n个MG):

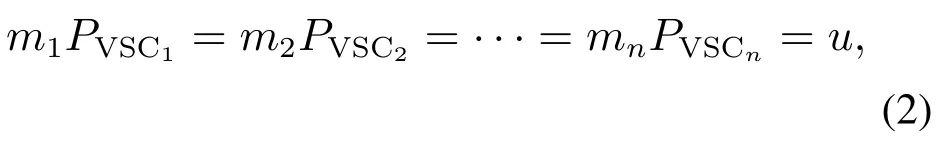
目前,也已有类似研究,如文献[25]中针对单一微电网内部机组的功率分配策略,即在不考虑经济性的前提下,是通过改进下垂系数,来实现各机组按照下垂系数比例来输出有功功率的.这种情况下,各机组之间需要满足条件Pn).而本文的研究架构也借鉴了该思想,即各微电网需要承担的功率是根据VSC之间的调控系数比例来分配的,即需要满足

两篇文章的区别就在于,本文针对微电网内部的各机组,还考虑到要降低发电成本,就对机组的出功又做了优化分配,并没有按照下垂系数来均分.

3 MG内的控制架构

对于MG内部而言,主要是确保DER与储能设备的输出电压稳定和有功功率得到均分.为实现这两个目标,本文分别设计了电压二次控制器和电流调控策略,具体如下.

3.1 设计电压二次控制器

当计算出每个MG对应VSC应该输出的电压后,就要调节MG中各个DER的输出电压达到该值.在本文中,电压是通过二次控制结合反下垂控制来调控的.其中,电压二次控制器又是基于通信数据和一致性算法实现的,因此先给出如下定义,以便解释后续控制器的设计.

MG通信网络[25]:MG的通信网络包括传感器,用于搜集物理数据;上传信道,用于上传物理数据;执行器,用于在网络中完成所需的控制器或算法,如一致性算法等;下发信道,用于将由网络中的控制器或者算法得到的控制量等下发至物理系统,改善物理层中对应环节的运行效果.

图论[26–27]:对于一个有向图而言,一旦存在一条有向路径连接到所有的节点,该路径就被称为“有向生成树”,其初始节点就被称为“根节点”.而为了描述节点之间的连接关系,参数aij就被设定了出来:如果第j个DER的数据被输送至第i个DER,aij就被置为1;否则aij=0.

一致性算法[26–27]:在一个有向图中,将第i个节点的信息数据置为xi.那么,当有一个初始节点的数据被输送至其他节点,即有向树存在,那么该初始节点就被称为“领航者”,其他节点就被称为“跟随者”.领航者的信息数据被记为xL.基于该生成树,如果有算法可实现条件,那么就说每个跟随者的信息都与领航者的信息达到了一致.该条件对应的算法也就是一致性算法,即式(3).

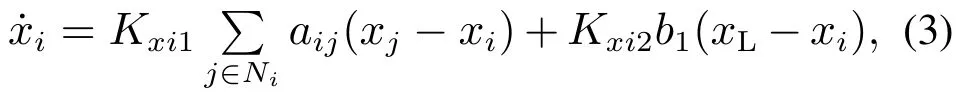
其中:bi代表第i个跟随者能否接收到领航者的信息数据,如果能,那么bi=1.否则,bi=0;Ni代表第i个节点的相邻节点的集合;Kxi1和Kxi2代表增益参数.

注1实际上,MG系统中的每一个DER都是一个节点[26],但在MG系统中选择领航者并不方便.因此,本文采用“虚拟领导者”来解决这一问题.它的实现只需将xL设计成一个固定值(如电压或频率参考值),并直接送入一致性算法中.这样,只要合理地设置aij和bi以保证有向生成树存在(在该树中,“虚拟领导者”是根节点),一致性算法的控制效果就得到了保证.

3.2 阐明二次控制架构和过程

对于MG中的DER和储能设备而言,其一次控制一般都是下垂控制.并且,在孤岛交流微电网中,分布式电源的输出电压有限,一般都是低压网.而对于低压网而言,线路的阻感比是比较大的,即线路多呈现阻性.因此,传统的适用高压电网(线路阻感比较小)的P–f/Q–U下垂控制并不能直接应用于低压MGC中,而是需要添加虚拟阻抗[28]或采用其他方法来使线路呈感性后,才能被应用.

综上,为适用于孤岛低压MGC,本文直接采用了反下垂控制策略(即P–U/Q–f下垂控制).这样,MG中各电源的输出电压将主要由有功功率决定,本文就仅考虑了有功功率的平衡约束.并且,也有相关文献采用了类似的方法,如文献[25,29].以第i个DER为例,其数学表达式如下:

其中:mi是下垂系数;Uref是电压参考值;Pi是第i个DER输出的有功功率.

但反下垂控制本身就是有差调节,并且一旦有负载扰动发生,就会使得DER的输出电压也发生抖动,两者呈线性关系.并且,每个DER的下垂控制系数不同,对应的线路阻抗也不同,因此很容易导致输出的电压是不一致的.这样,就会导致出现环路电流.为了解决上述问题,就应设计二次控制来给下垂控制添加反馈量,以调节其输出达到设定的参考值.本文中,依然以第i个DER为例,其电压反馈量被设计为

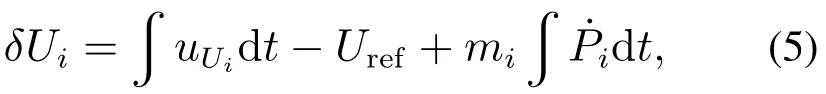
其中:uUi是电压二次控制器;δUi是电压反馈量;代表积分运算.在二次控制过程中,δUi将被添加入下垂控制的输出电压,以抬高电压值.一般而言,uUi被设计为[30–31]

其中:Ui和Uj代表第i个DER与第j个DER(或者储能设备)输出的电压值;UL代表领航者的电压值;KUi1和KUi2都是增益系数;Ni代表第i个DER的相邻发电设备的集合.

在电源逆变器控制回路中,根据反下垂控制公式Ui=Uref−miPi可知,输出电压Ui与参考值Uref将存在偏差.为解决该问题,就需要为Ui添加增量δUi.同时,考虑到要实现各DER的同步调控,本文就基于一致性算法,设计了如式(5)所示的增量,即δUi=而在添加该增量后,也需要令最终趋向于Uref.因此,文中采用了(virtual)leader-following一致性算法,即式(6).对于该类一致性算法而言,只需要保证通信拓扑存在有向生成树并设定(virtual)leader为根节点,就能实现各被控电源的状态量最终同步趋向于UL.基于该特性,在本文中,仅需要设定UL为Uref即可.

3.3 有功功率调控

对于MGC中的有功功率调节而言,考虑到要最小化发电成本,本文就提出了基于边际成本一致和考虑储能设备经济出功的调控策略,具体的设计如下.在交流MGC中,考虑系统中只存在DER与储能设备.以第i个MG为例,其中第i个DER的发电成本为[19–20]

其中:αi−i,βi−i和γi−i都是第i个DER的发电成本系数;αi−i表示发电成本曲线的曲率,通常αi−i >0;βi−i表示发电成本曲线的斜率,即发电成本随发电功率增加的速度;γi−i表示发电成本曲线的截距,它与发电机组空载损失有关,一般为正值.如果发电成本中包括固定成本(如建筑成本等)的话,主要反映在γi−i中[32–33].是第i个DER的有功出力.对于储能设备而言,当其SOC值处于正常范围时,其充放电效率与输出功率是线性关系,即

其中:为第i个MG内储能设备的充放电效率;和为储能设备发电参数,与储能硬件参数、容量、使用寿命相关;为对应储能设备的有功出力.储能的运行成本函数为

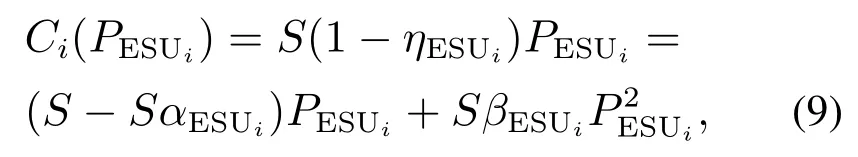
其中:S是实时电价.因此,第i个MG的总运行成本为

此外,也需要确保如下等式约束是成立的,

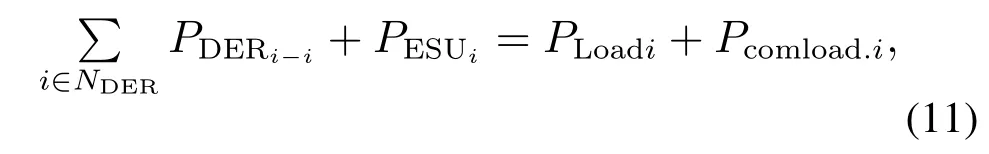
其中:PLoadi是第i个MG中负载所需功率;Pcomload.i是第i个MG需要为公共负载提供的能量;NDER代表可控DER的个数.对于上述有约束单目标优化问题,引入了拉格朗日乘子后,得到

进而,再令式(12)对DER和储能设备的出功求偏导数得到

在拉格朗日乘子法中,边际成本的计算仅涉及式(7)(11),都呈二次函数关系,是凸函数.并且,已有文献[19,33]说明,采用拉格朗日乘子法能得到最优解.这是因为,拉格朗日法一般都是求极小值,而对于微电网供电系统而言,仅有一个极值点,即.因此,该极值点也是最值点.

注2由文献[18–23]可知,对于光伏、风机等可再生能源而言,其发电成本基本为0.因此,在优化发电成本时,该二次函数模型仅适用于模拟可控DER(例如燃料电池、柴油机组等)的发电特性.并且,本文考虑的式(10)中,也是仅考虑要调节可控DER的输出有功功率.由于MG中包含多类可控DER,每一类DER的发电成本系数不同,因此不能直接计算出整个MG的发电成本系数.这样,整个MG的边际成本就无法计算得到.本文就在MGC层面采用按容量比例均分的策略来为每个MG分配需要提供的有功:而对MG内的发电设备则基于边际成本一致的思想来调控各DER输出的有功功率,以实现发电总成本最低.

为了使发电设备都实现最优出功,本文提出了一种电流调控法,具体的设计见下节.

3.4 设计电流调控策略

以往的文献中(例如文献[18–23]),需要将各出力机组的边际成本都调节到一致后,才能计算出各自对应的调节量,以实现出功的最优分配.而该类算法的使用就避免不了要应用机组间的稀疏通信网络和数据交互.因此,这就避免不了会添加通信网络和通信成本,并且需要一定的迭代时间才能完成出功调控.针对这些问题,设计了如下应对手段:

实际上,各电源最终对应的l值(记作l′)可以直接计算得到,即

这样,根据提前计算好的l′值,就可以计算出对应的有功功率为

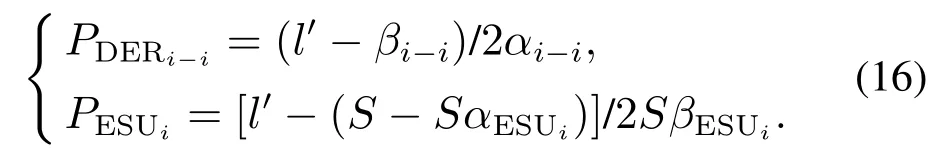
而实际上,对于第i个MG中的第i个发电设备而言,由文献[30–31]知,其有功功率公式为

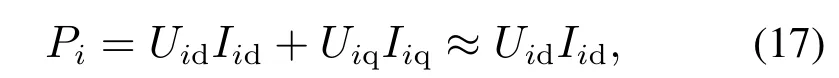
其中:Uid和Uiq分别是第i个发电设备的输出电压经过Park变换后得到的d轴和q轴分量;Iid和Iiq分别是第i个发电设备的输出电流经过Park变换后得到的d轴和q轴分量.基于式(17),和电压参考值(经过二次控制后,各电源输出电压将维持在参考值),由于Uid≈Ui,就可以按式(18)选定电流值为

综上,可以发现,所提电流调控策略不必添加通信网络和一致性算法来迭代计算出最终的l值,而是直接根据式(15)即可反解出,进而就能利用电压参考值来选定各电源对应输出的电流值(可以通过调节阻抗值等方式来实现电流的调控).在上述过程中,本方法仅需要从物理层动作即可,不涉及添加可控机组之间的稀疏通信网络或者数据交互,既可以直接实现有功功率的经济性调控.综上,相对于现有文献[18–23],所提方法并不会增加通信成本.

综上,基于上述设计,本文提出的单一DER的控制结构如下图3所示.

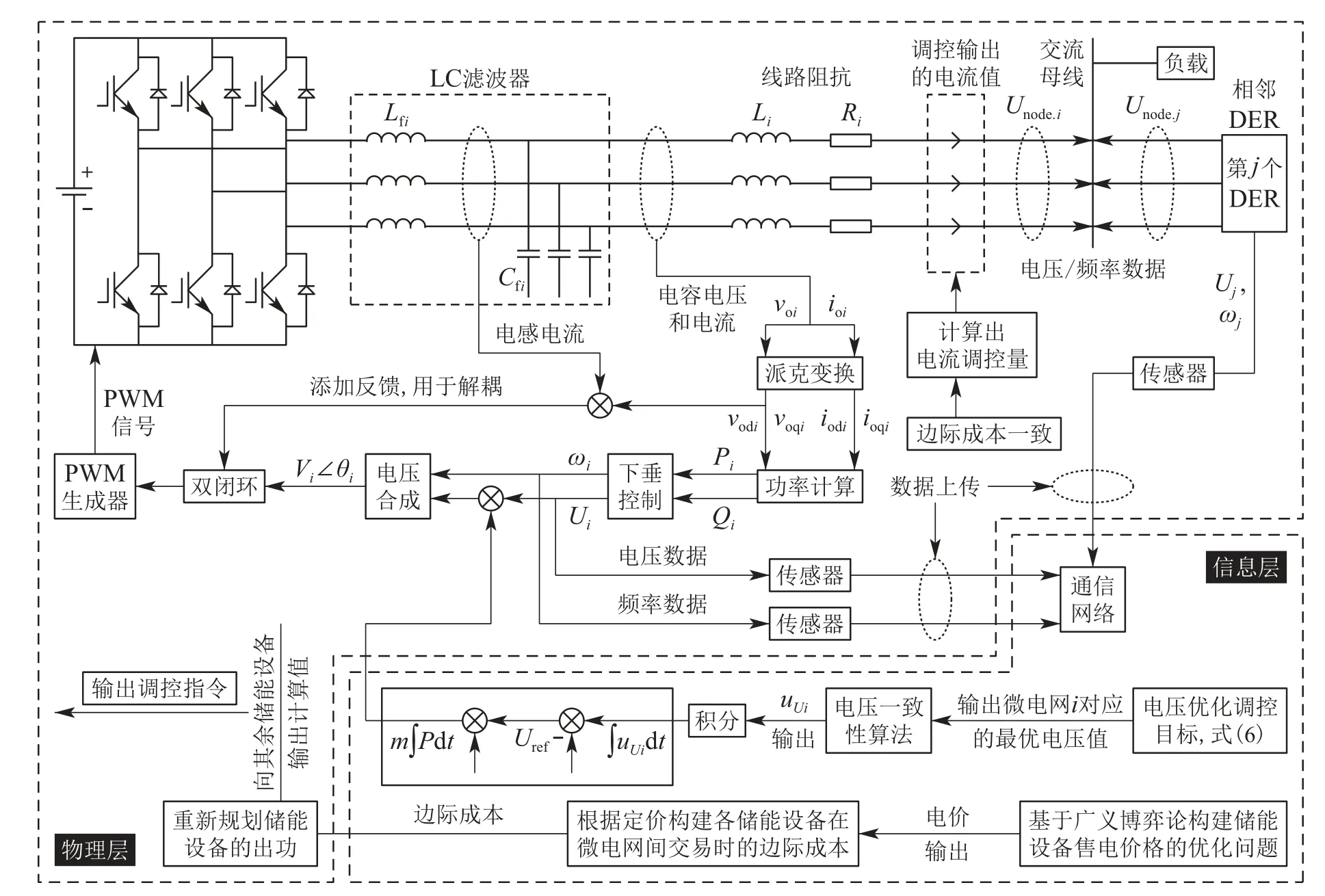
图3 在第i个微电网中第i个DER的控制系统Fig.3 The control structure of the i-th DER in the i-th MG

4 小信号模型法分析稳定性

在设计完电流调控环节后,虽然能得到最优输出功率,但由于DER的出功有上下限,因此就有

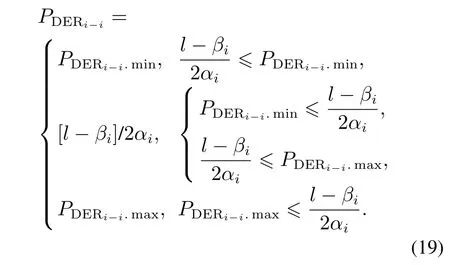
对于储能设备出功而言,是有出功上下限约束的,而该约束一般与自身的SOC值有关.在本文中,笔者设计:当SOC值小于下限或高于上限时,储能设备都将停止工作;当SOC值处于正常范围内时,将按照进行出功.该方案对应的数学表达式为

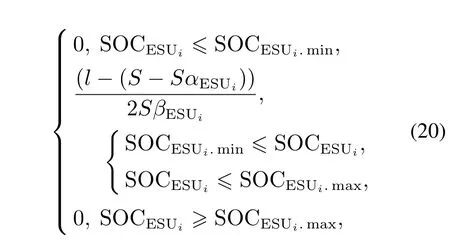
其中:是第i个MG对应第i个ESU的出功量;是该ESU的SOC下限;是该ESU的SOC上限.在文中,当储能设备的SOC值越限后,该设备就将停止工作.后续将根据边际成本一致准则,按式(15)重新求出新的l.后,再重新给其余不越限的可控机组分配新的供电方案.

综上,由于各DER输出的电压在二次控制的作用下是稳定的,因此通过改变输出电流值,就完成了对于输出有功功率的调控.但是,由于DER与储能设备的出功都是有最大和最小值限制的,因此这些发电设备会发生工作模式的改变.例如,DER会从二次控制模式转变为恒功率模式,储能设备会从发电模式转变为放电模式等.所以,还需要再分析当电力设备中添加了二次控制后,或者发电设备的运行模式发生了转变等,会对该设备运行稳定性的影响.

4.1 小信号模型分析在添加策略后对发电设备稳定性的影响

由于电压的二次控制与有功功率的调节都会对每个发电设备自身的控制环造成影响,并且DER与储能设备在运行过程中还会发生模态转变,因此本文建立了小信号模型来分析如何确保每个发电设备自身的控制环依然能稳定.以第i个DER为例,分别分析电压二次控制和DER工作模式的转换会对稳定性所造成的影响.

4.1.1 分析电压二次控制对DER控制环造成的影响

第i个DER(即DERi)的输出功率为

其中:Zi和θi分别是线路阻抗的幅值和相角;φi是输出电压Ui的角度;PLocal和QLocal代表本地负载的功率需求.

注3文中之所以将可控机组的发电成本描述为二次函数的形式是因为参考了相关文献[19–23].而本文中小信号模型分析采用的式(19)是根据电源出功关系得到的,即输出功率与电压幅值、相角、阻抗等物理量有关.之所以建成式(19)的形式是为了便于分析当控制环路中存在电压干扰或者相角干扰时,如何选择合适的控制参数,才能维持该控制系统的稳定运行.而文中式(7)则是指各可控DER按照式(19)出功后,其发电成本与有功出力是呈二次函数关系的.并且,发电成本是基于出功得到的,二者有先后顺序,即先由式(19)得到出功后,才能根据式(7)计算出发电成本.综上,文中采用二次函数来描述发电成本,用非线性函数来描述电源的出功模型,两者并不冲突.

当经过滤波后,有功功率和无功功率变为

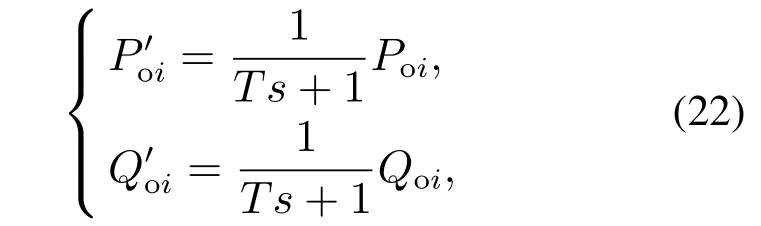
其中T代表滤波时间常数.如果考虑在系统中发生了电压扰动和频率扰动,就有

当考虑在系统中添加了电压二次控制器后,有

小信号稳定分析的目的是想验证当某机组的控制过程中出现小干扰后,是否会影响其正常输出其他物理量[25],分析过程如下:首先,本文以控制过程中突发小扰动∆U和∆φ为例,基于式(19)–(21),可知无功变化与∆U和∆φ呈线性关系,即扰动会导致出现无功功率的变化;其次,基于无功功率与相角之间的数学关系式(即式(22)–(23)),可知∆Q与∆φ呈积分关系,即无功功率的变化又会导致后续出现相角的变化;再次,由于相角与电压之间的关系(即式(22)–(23)),可知在频域中,∆φ和∆U呈现非线性关系,即相角的变化也会引起电压的变化;最后,基于式(19)–(21),可知后续无功功率的变化又会受到相角变化量和电压变化量的影响.

因为初始时刻下,控制过程中出现的小干扰为暂态输入,因此最终也希望∆Q将被抑制到0.故将零输入作为系统的前向输入.综上,即可构建如图4所示的控制架构图.其中,实线部分代表当DERi中不添加二次控制时的控制架构,而虚线部分是指当DERi中添加二次控制后的控制架构.

根据图4,文中将添加二次控制前后的闭环传函分别表示为

图4 DERi的控制环路图Fig.4 The control loops of the i-th DER

和

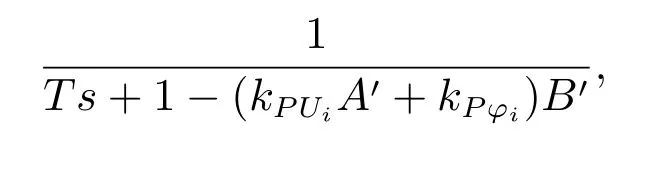
其中:

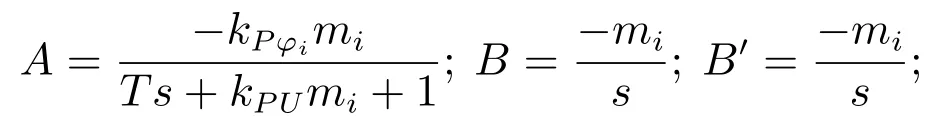
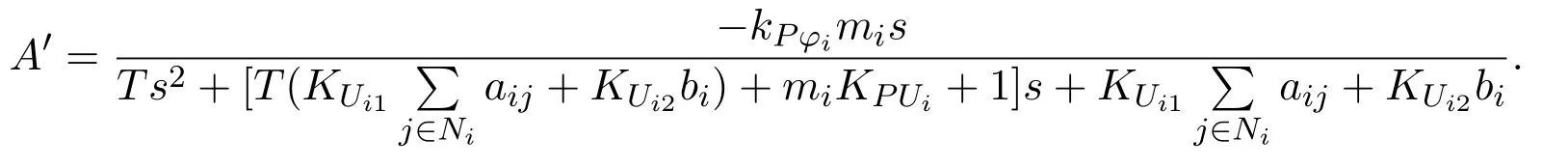
因此,如有要维持闭环控制系统的稳定性,就需要在一致性算法中设计合适的增益参数,以确保闭环传函的特征根都具有负实部.

4.1.2 DER工作模式的转变会对其控制环节造成的影响

同理,通过类似的过程就能分析DER工作模式的转变将对其控制环节所造成的影响.在本节中依然以系统中发生了电压和频率扰动为例,来构建DER控制系统的小信号模型.对于DER的二次控制,就如式(5)–(6)所示.而DER的恒功率运行模式一般就是指功率将经过添加前馈电流后,被直接当作电流环的输入,而DER的输出电压和频率将由各DER自身调控.在这种情况下,以第i个MG中的DERi为例,得到其恒功率控制模态如下式:

其中:Pconst和Qconst分别代表有功恒定值和无功恒定值.这样,无论在输出电压和频率的过程中是否有扰动发生,都不会影响正常的功率输出.即,在恒功率控制下,电压和频率扰动就仅仅对电压和频率有影响.当考虑第i个DER从二次控制模态切换至恒功率运行模态的情况,就有

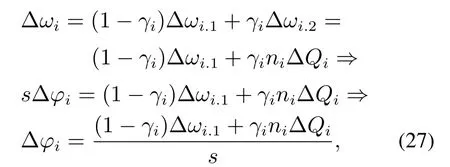
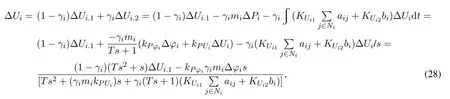
其中0 ≤γi≤1.当γi=0时,就代表DER工作于恒功率模态;当γi=1时,就代表DER工作于二次控制模式.而当0<γi <1时,就代表DER正处于模态切换的过程中.由于DER会发生模态切换,因此该切换过程就被描述为一个多输入+多输出系统.这样,根据叠加定理就得到了闭环传递函数,相关系统框图如图5所示.

对于图5所示的多输入+多输出系统,经过叠加定理后得到闭环传函为

图5 叠加定理下的两个子系统Fig.5 Two subsystems under superposition theorem

5 仿真案例及分析

在仿真实验中,采用的MGC模型如图6所示,即包含3个MG,每个MG中都包含信息层和物理层.其中,物理层包括3个DER、1个储能设备、控制环、电流调控环节、本地负载和扰动负载等;信息层包括传感器和电压二次控制器等.并且,每个MG都是经过VSC并联在公共母线上,并为公共负载供电的.该模型中所对应的仿真参数如表1所示,其中aij.other=0代表其余DER之间并未连接.

表1 相关的仿真参数Table 1 The related simulation parameters

5.1 案例1:稳定性分析—验证所选用的一致性控制系数是否合适

由图7可见,基于所选用的一致性系数,无论何种情况,都能保证闭环系统的特征根都分布在虚轴的左侧.这样,就能确保在运行过程中,各发电单元都能稳定运行.即,所选用的一致性系数是合适的.

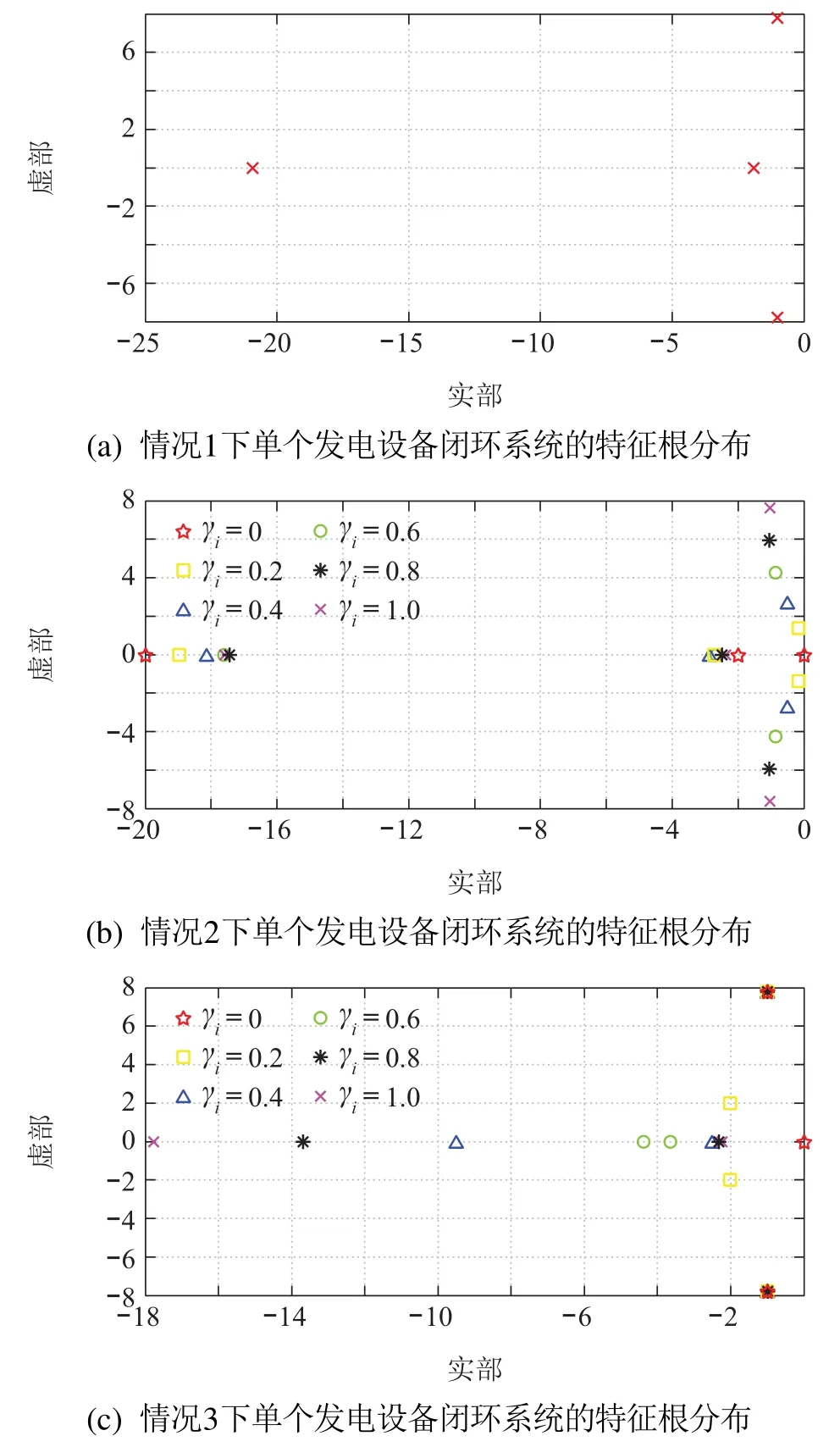
图7 特征根分布图Fig.7 Distribution of eigenvalues in closed-loop system of single electrical device

5.2 案例2:验证电压调控的效果

在本试验中,以图6所示的微电网为例,分别模拟了当MGC中的DER仅采用下垂控制和采用二次控制的控制效果.其中,二次控制被添加的时间为t=0.25 s.该仿真实验结果如图8和图9所示.文中,对于DER1–DER3和储能设备的调控结果分别被标记为不同颜色:黑色–DER1;粉色–DER2;蓝色–DER3;红色–储能设备.

图6 仿真实验所用MGC模型Fig.6 The used MGC model in simulation experiments

不采用电压二次控制时各变量的变化如图8所示,其中电压的调控结果如下:由于DER1所对应的下垂系数mi是其余DER对应下垂系数的2倍,并且由于线路阻抗存在差异的原因,就使得DER1输出电压最终稳定于310.5 V,而其他3个DER的输出电压稳定在310.75 V左右.并且,当系统中扰动负载动作时,各DER的输出电压值会在0.5 s和1.5 s分别上升与下降.

有功功率的调控结果如下:由于各DER对应的线路阻抗与输出的电压都不一致,4台DER的输出有功功率也是不能按照容量比例输出的,即与传统的P–ω/Q–U下垂控制的效果正好相反.DER的出功都基本为25 kW.并且,当扰动负载在0.5 s添加后,DER的出功都一起变为34.5 kW.在1.5 s后,出功又重新恢复至0.5 s前的状态.频率与无功功率的调控结果如下:由于系统采用反下垂控制,因此随着无功功率的增加,各DER输出的频率也是增加的.不过,由于频率的输出基本与线路阻抗是无关的,所以各DER的输出频率都一致,而无功功率就按照n1Q1=···=n4Q4被合理分配.当系统中扰动负载动作时,频率值和无功功率值也会在0.5 s和1.5 s分别上升与下降.

二次控制的效果如图9所示,电压调控结果如下:在1 s前,各DER的输出电压都与图8(a)中的变化情况一致.但当在1 s时引入电压二次控制器后,就会使得输出电压逐渐的趋于311 V,并且即便1.5 s时扰动负载被切除,也不会对电压值有任何影响;功率调控结果如下:由于有功功率与输出电压值直接关联,而在二次调节下,电压值会趋于一致,因此有功功率也会在1 s后有一段暂态过程.并且,会跟随扰动负载的动作而变化.频率与无功功率调控结果如下:由于仅设计了电压二次控制器,因此各DER的输出频率与电压基本与图8(c)和8(d)的变化一致.

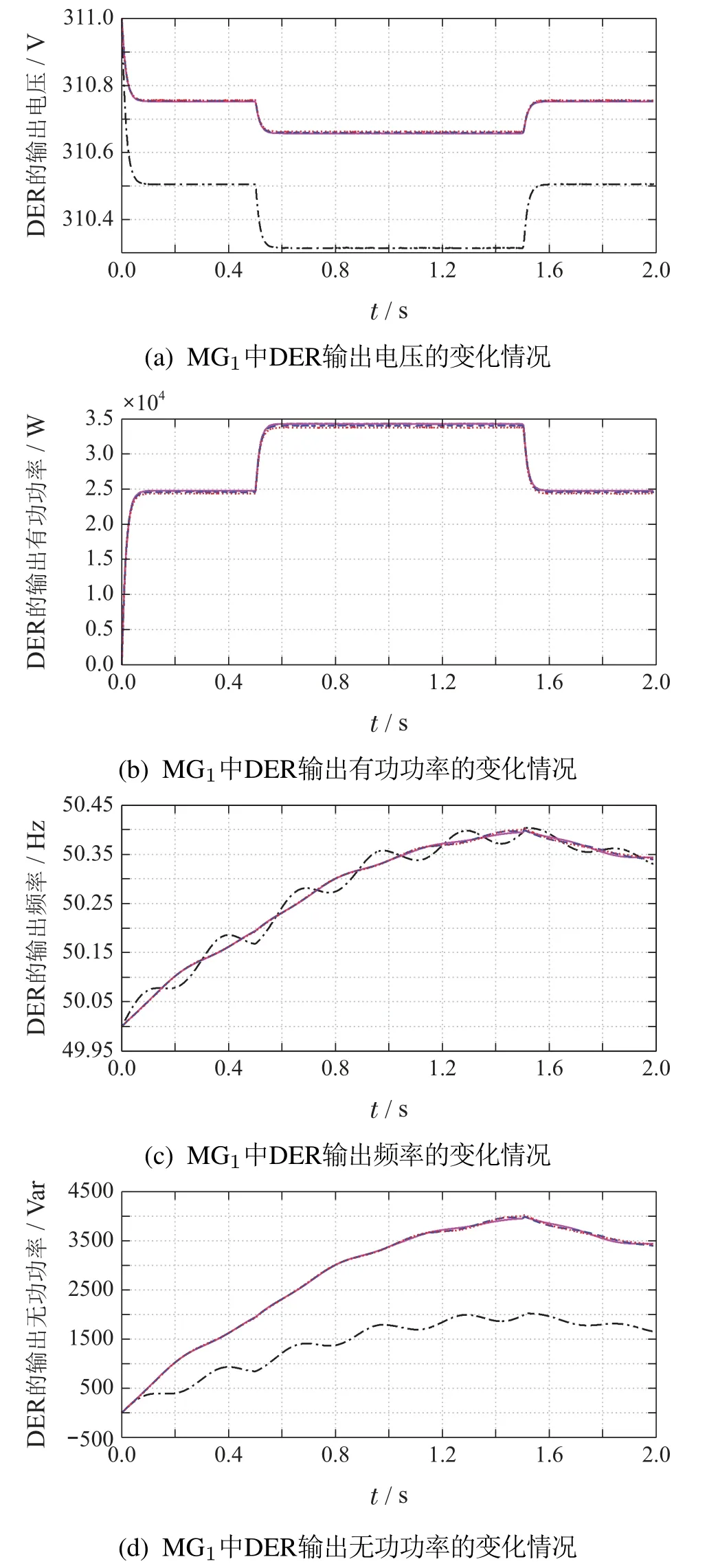
图8 仅采用下垂控制的效果图Fig.8 The control effect of droop control

将仿真图9与文献[11]中的仿真结果对比可知,本文所采用的反下垂控制不必设计虚拟阻抗,就可以实现有功功率的稳定输出,并且能迎合负载的需求变化.此外,基于本文提出的二次控制策略,能实现电压在1 s内就恢复至参考值,且并不受外界扰动的影响.

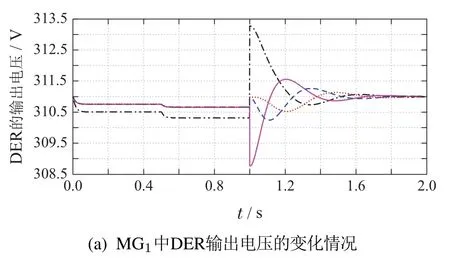
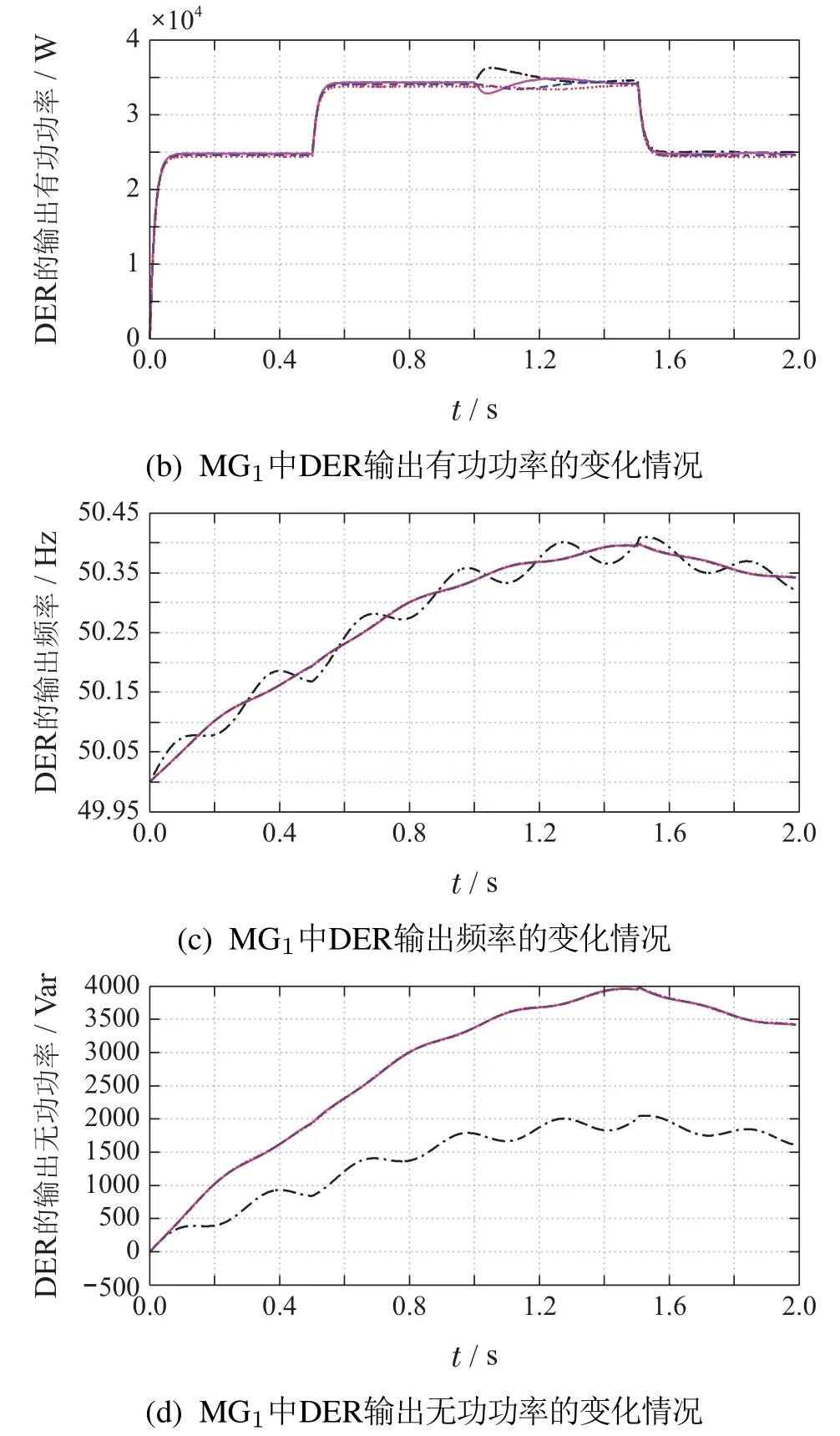
图9 电压二次调控的效果图Fig.9 The control effect of secondary voltage controller

5.3 案例3:验证有功功率调控的效果

在该案例中,以图6中的MG1为例,分析所提出的电流调控方法的调控效果.并且,试验中所涉及到的成本系数如下表2所示(借鉴文献[19]).具体的仿真情景如下:首先,各DER与储能设备都将按容量比例出功;然后,在t=0.5 s和t=1.5 s增添或者删去了扰动负载;最后,分别在t=0.2 s,t=1.2 s和t=1.7 s在系统中进行了电流调控,以验证有功功率是否能够被最优地分配.此外,在t=1.5 s后,又在系统中添加了负载,以判断当有DER达到出功上限时,MG1中各设备的运行情况.仿真结果如图10–12所示.

表2 案例中涉及的成本系数Table 2 The related cost parameters in this case

当不在MG1中添加电流调控时,如图10和图11所示,各发电设备输出的边际成本将仅跟输出功率与成本系数有关,分别为0.328,0.185,0.169和0.119.并且,当扰动负载动作时,边际成本也会在0.5 s和1.5 s发生突增和突减.与之对应的,各发电设备的发电成本如图10(b)和图11(b)所示.其直接与输出功率呈平方关系.并且总成本为$16.04(不添加扰动负载时)和$24.56(添加扰动负载时).

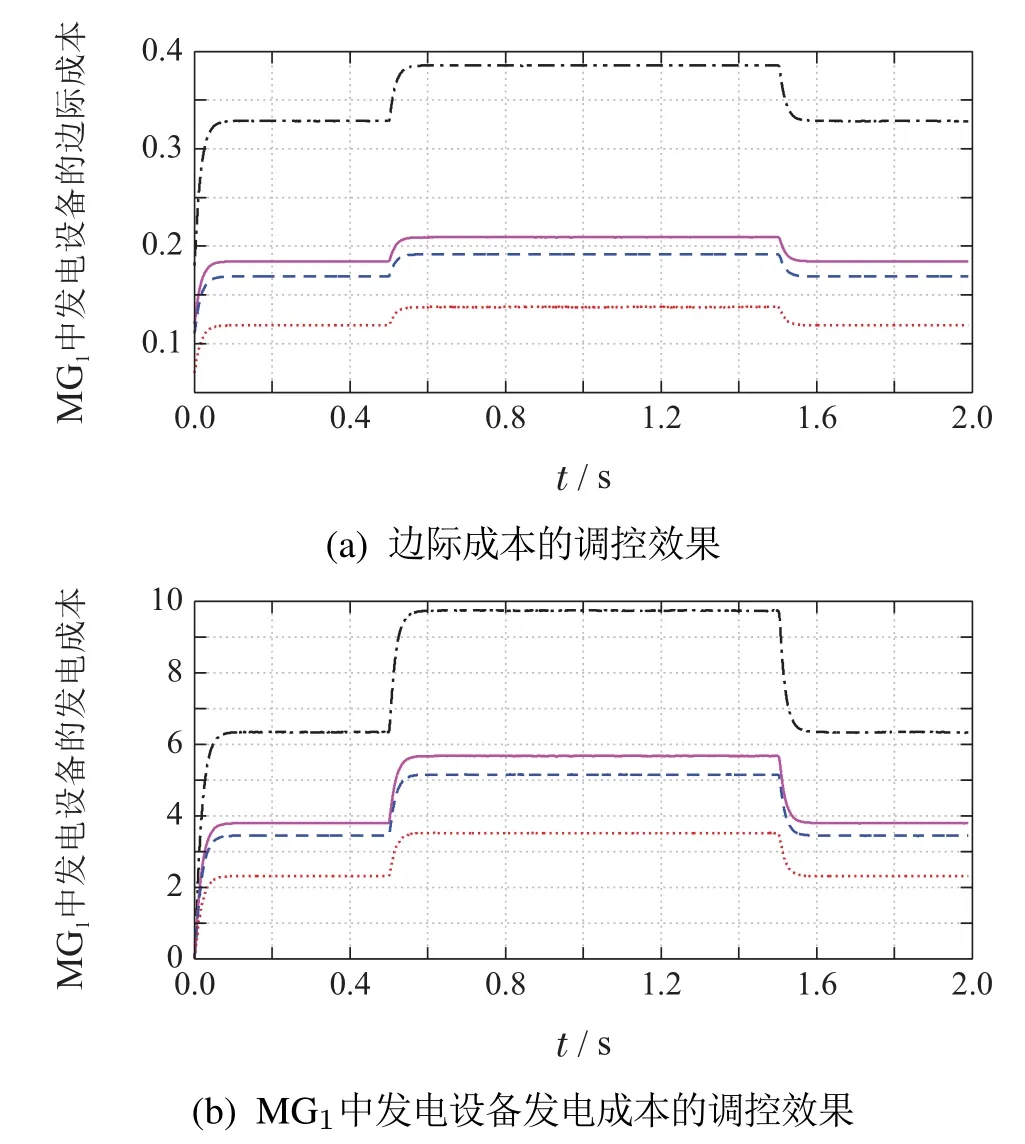
图10 仅采用下垂控制时MG1中DER的运行成本情况Fig.10 The regulation effect of generation costs of DERs in MG1 with droop control only

图11 仅采用电压二次控制策略时MG1中DER的运行成本调控情况Fig.11 The regulation effect of generation cost of DERs in MG1 with secondary voltage controller only

当在MG1中添加电流调控后,仿真结果如图12所示,发电设备的边际成本将立即归于一致,分别为0.174(不添加扰动负载时)和0.2(添加扰动负载时);而在电流调控下,各发电设备的输出有功功率也会跟随边际成本发生变化,即0.5 kW,4.91 kW,5.61 kW 和8 kW(不添加扰动负载时)和0.95 kW,3 kW,3.3 kW和6.1 kW;而MG1系统的总成本分别为$13.2(不添加扰动负载时)和$19.22(添加扰动负载时).

综上,在使用电流调控后,就实现了MG1的发电总成本节约了$2.84(不添加扰动负载时)和$5.34(添加扰动负载时).

将图12与文献[18–19]中的仿真结果做对比,可知本文所提有功功率调控策略不涉及迭代过程,仅需要提前计算出各电源的最优出功量,即可实现经济性调控.并且,该调控不必经过迭代过程,即确保了控制的实时性,其可以有效迎合有机组出功越限的情况,及时更正各机组的边际成本和最优出力.另外,由于调控并不涉及一致性等基于数据通信的算法,因此不会引入通信问题.

注4在图12(b)和(c)中,DER1的输出有功和发电成本是负值,这是因为此案例中没有对DER的出功设定限值.

考虑到功率限制,本文中又进行了如下仿真实验:基本的实验过程同上,仅对两处进行了修改:1) 电流调控动作的时间变为0.2 s,0.5 s和1.5 s;2)只是将DER1和储能设备的出功范围修改为5～50 kW和0～50 kW(本文所设计的有功功率调控策略是为了规划好各电力设备的最优出功,即主要考虑如何以发电成本最少为目标,最优化调控各可控机组的有功出力.而由于储能设备在充电时,并不会涉及发电成本问题,因此本文在文中就将储能设备的出功下限设定为0～50 kW).仿真结果如图13所示.

仿真分析如下:在0.2 s后,各DER的边际成本并不一致,分别为0.21,0.174,0.174,0.17.而DER1和DER4的出功也被限制在5 kW和50 kW.并且,发现即便扰动负载在0.5 s被添加或者在1.5 s被剔除,这两个DER的出功始终会被维持在限定的范围内.而对于DER2和DER3而言,他们的边际成本会在0.5 s和1.5 s达到新的一致值,即0.216和0.169.由图13(c)所示,在限定了发电设备出功后,MG1的总共发电成本为$12.35(不添加扰动负载时)和$21.4(添加扰动负载时).通过比较图10–13,发现虽然在限定了发电设备出功后,MG1的发电成本较图12(c)有所增加,但仍然低于图10(b)和图11(b)的优化结果.并且,图12所示的结果更契合实际微电网系统的运行情况.

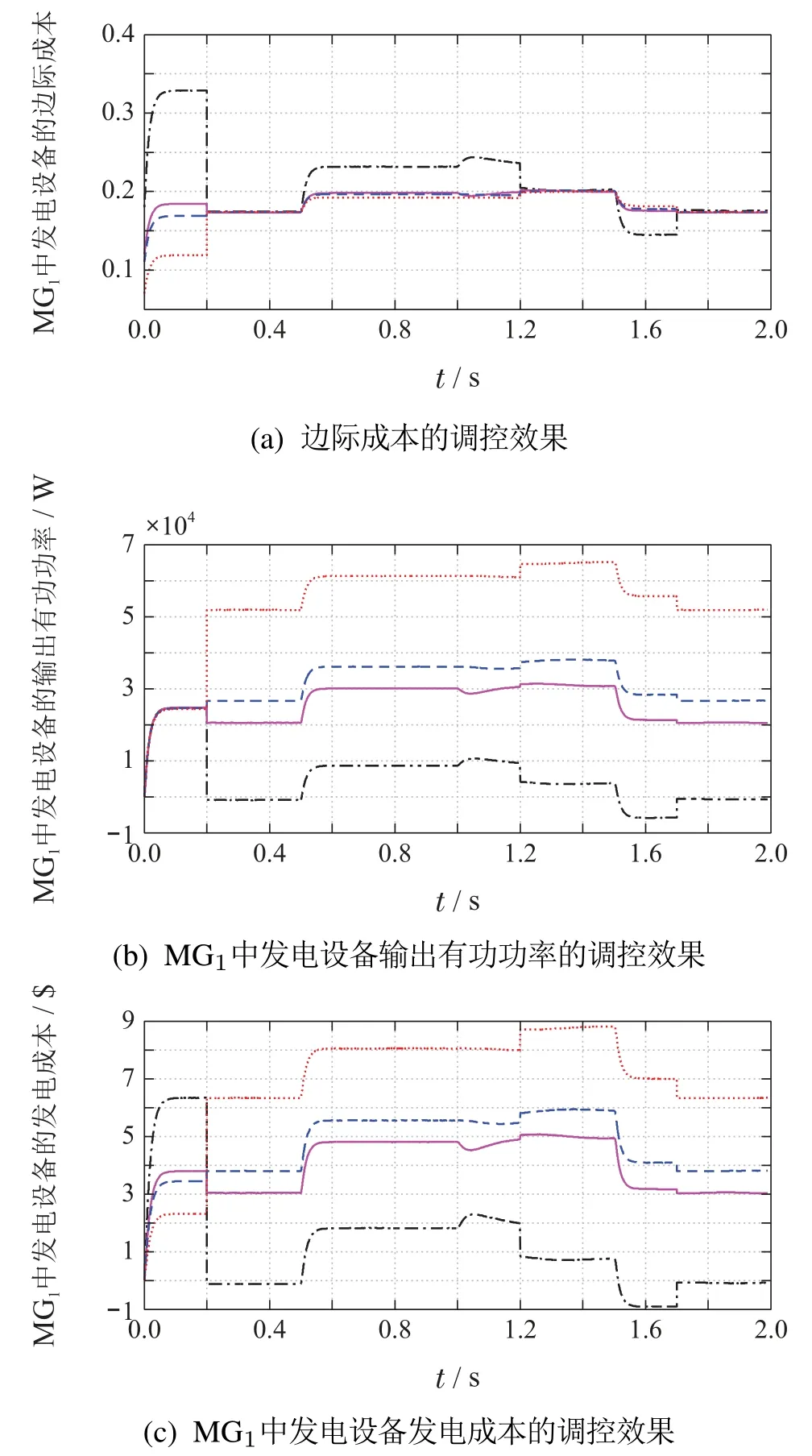
图12 添加电流调控后MG1中的控制效果Fig.12 The regulation effect of MG1 with current adjustment

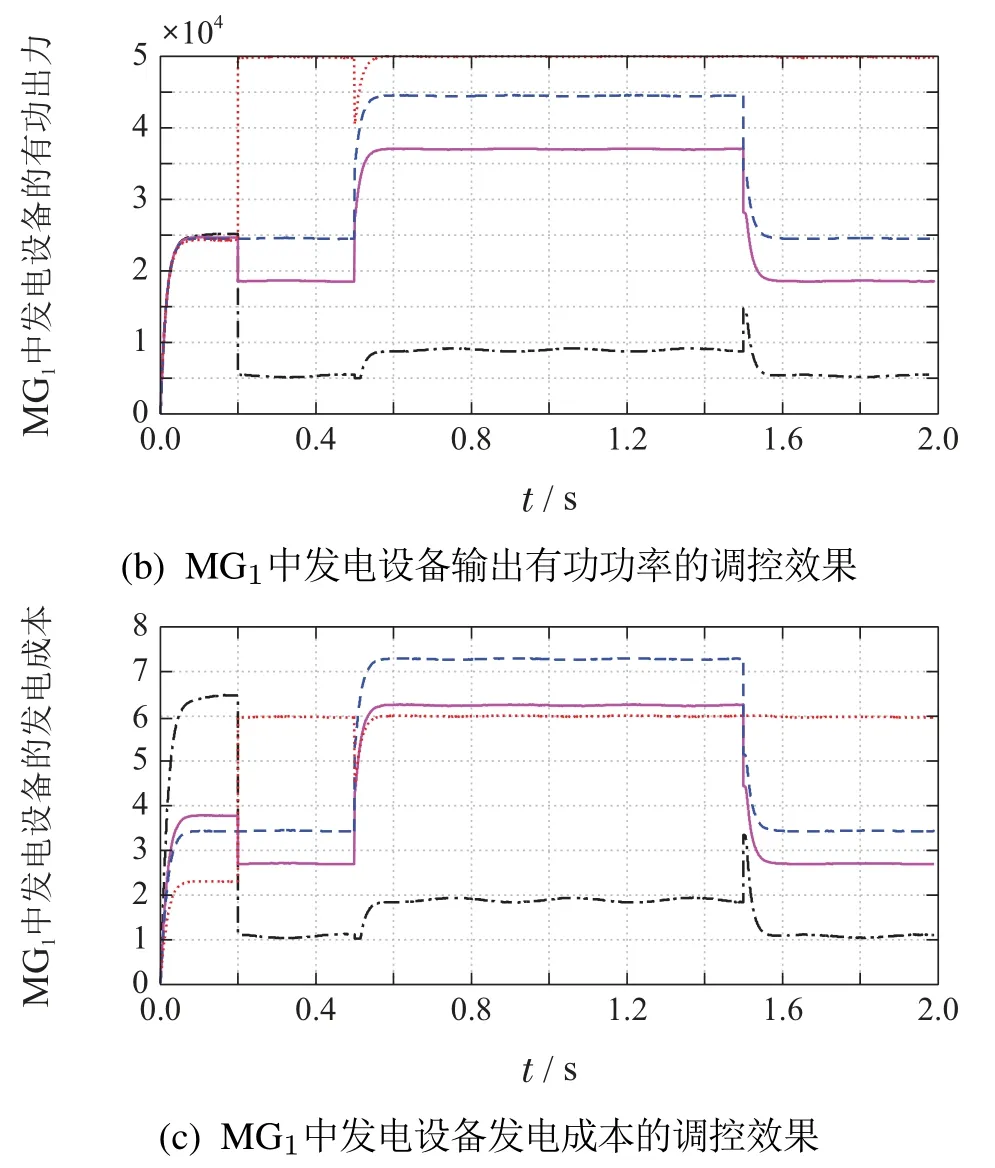
图13 当考虑DER1和DER4有出功限制时电流调控的效果Fig.13 The regulation effect of current adjustment when the output power of DER1 and DER4 is limited

6 结论

对于孤岛交流MGC中各MG的电压稳定和有功功率均分问题,文中分别提出了如下的调控策略:1)给定了电压调控目标,并设计了电压二次控制来调节各MG中DER的输出电压;2) 将储能因素考虑进了边际成本一致性调控中,在使得发电成本最低的目标下,设计了电流调控策略以使得各发电设备实现最优出功;3)利用小信号模型,分析了提出的上述策略对单个发电单元运行稳定性的影响.最终,仿真案例1验证了所选用的控制系数可以有效维持单个发电设备的稳定运行;仿真案例2验证了所提出的电压调控策略能有效将微电网中各DER的输出电压都调节至一致,最终能达到并稳定在预期的参考值;仿真案例3验证了所提出的有功功率调控策略有效实现了各DER的最优出功.在限定出功的情况下,文中提出的电流调控策略将发电成本降低了$4.05和$3.16.后续,将针对MGC的频率稳定问题展开相关的研究工作.