通信拓扑切换下车辆队列分布式模型预测控制

罗 捷,鲁良叶,何德峰 ,俞 立,杜海平

(1.浙江工业大学信息工程学院,浙江杭州 310023;2.伍伦贡大学电气与计算机和通讯工程学院,澳大利亚伍伦贡2522)

1 引言

车辆队列作为提高交通效率和道路安全性的一种有效途径,近年来受到了广泛关注[1–3].通过对队列的先进控制,使一组车辆相互协作形成一致的队形,并保持安全间距和相同速度行驶[4–5].目前,许多学者采用分布式模型预测控制(model predictive control,MPC)方法来解决不同约束条件下的车辆队列协同控制问题[6–9].在车辆队列的分布式MPC框架中,通常利用关联车辆的状态信息建立局部控制目标,同时车辆在运行过程中需要满足特定的空间约束[8–9].

队列系统的稳定性是车辆队列系统研究的关键问题之一.文献[7]通过对局部最优代价函数求和,在分布式MPC框架下建立了非线性车辆队列系统的稳定性.文献[10]针对线性系统的队列控制问题,提出了具有耦合约束的鲁棒分布式MPC策略.除了队列系统的稳定性外,研究人员对队列系统弦稳定性做了大量工作[11–13].车辆队列的弦稳定性要求前车干扰信息不能沿着车队反向传播.文献[12]提出一种能够同时保证特定通信拓扑下车辆队列系统稳定性与弦稳定性的分布式MPC策略.进一步,文献[13]提出一种保证特定车辆队列γ增益稳定性的分布式MPC策略.

在车辆队列分布式MPC框架中,通信拓扑对车辆队列控制效果有着显著影响.车辆队列分布式MPC策略通常采用前车–跟随车(predecessor-following,PF)通信拓扑结构[7–9,12],而文献[13]采用固定的前车–跟随车–后车(predecessor-following-successor,PFS)双向通信拓扑结构.文献[8]分析了不同通信拓扑对异质车辆队列系统队列控制性能的影响.由于无线通信距离的限制,大型队列系统通常不采用单一的拓扑结构,而是采用多种通信拓扑结构并存的通信方式[1].进一步,考虑高速行驶车辆驶入和驶出车队情况,可扩展车辆队列系统的通信拓扑需要频繁地更新,而通信拓扑的频繁切换会放大通信故障、网络攻击、网络拥塞等恶劣通信条件对车辆队列控制产生的不利影响[14–17].从网络化系统的角度来看,通信拓扑的变化会引起车辆队列控制系统的切换现象.车辆队列系统的切换现象意味着通信拓扑的改变可能会破坏切换前原始通信拓扑下车辆队列系统的稳定性.

另一方面,在切换系统与控制理论中,平均停留时间(average dwell-time,ADT)概念是一种用于处理切换控制问题的重要方法[18–21].文献[22–23]研究了通信拓扑切换对线性多智能体系统的影响.文献[24]采用比例–积分型控制律处理具有动态通信拓扑的线性车辆自适应巡航控制问题,提升了车辆巡航控制系统在动态通信拓扑下的控制性能.文献[25]采用Lyapunov-Razumikhin 定理与Lyapunov-Krasovskii定理证明了通信拓扑切换下线性异质队列系统的全局渐近稳定性.据笔者可知,目前针对通信拓扑切换下队列系统的控制研究成果仅适用于线性车辆队列系统,且无法显式处理车辆队列系统的位置误差、速度和加速度变量的约束条件.

针对具有系统约束和通信拓扑切换的异质非线性车辆队列系统,本文提出一种新颖的车辆队列分布式MPC策略.通过在线求解局部滚动时域约束优化控制问题,计算异质非线性车辆队列系统的分布式MPC控制律,其中,车辆的局部代价函数由其自身的暂态代价函数和平均协作代价函数构成.基于动态图描述的动态通信拓扑,平均协作代价函数由关联车辆的状态信息组成,体现车辆队列协作控制目标.引入平均停留时间概念与切换系统Lyapunov稳定性理论,建立保证通信拓扑切换下分布式MPC优化问题递推可行性和队列闭环系统稳定性与弦稳定性的充分条件.最后通过两组仿真实验验证本文结果的有效性.

符号说明:Rm表示m维实数向量,Rm×n表示m×n维实数矩阵.令符号I表示非负整数集合,且I[m,n]表示集合{i ∈I:m≤i≤n}.符号Im表示m维单位矩阵.若给定一向量x ∈Rm,|x|表示该向量的欧几里得范数,‖x‖Q=(xTQx)1/2为其权值矩阵范数,其中矩阵Q为半正定矩阵.

2 问题描述

考虑在同车道上行驶的有限n辆异质车组成的车辆队列系统.令车辆i ∈I[1,n]在t时刻的位置和速度分别为pi(t)和vi(t).该车辆队列控制目标为各车以恒速vdes跟踪理想位置轨迹si,des且与前车保持期望安全间距dr.定义车辆i∈I[1,n]的状态变量为xi=[ei∆vi]T,其中:ei=pi −si,des为车辆i实际位置与理想位置之间的位置误差,∆vi=vi −vdes为车辆i实际速度与期望速度之间的速度误差.结合车辆i ∈I[1,n]的理想轨迹,其跟踪误差动态过程可由如下二阶非耦合状态方程描述:

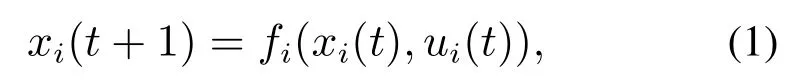
其中:误差状态xi(t)∈Xi,控制变量ui(t)∈Ui,fi为车辆动力学模型确定的非线性函数,Xi和Ui为包含原点为内点的约束集.注意在车辆队列中各车的误差状态方程彼此独立,即全车队的跟踪误差动态过程由n个非耦合的状态方程描述.不失一般性,原点为车辆跟踪误差系统(1)的平衡点.进一步,定义控制变量的约束为

其中常数umin,i <0和umax,i >0分别为控制量的上界和下界.

在车辆队列系统中,各车通过车载传感器和车联网获得邻居车辆的行驶信息.但由于环境限制和车队规模变化,车辆队列的通信拓扑在实际运行中可能会发生改变,导致用于队列控制的信息流发生切换.为此,先定义集合P:={1,2,···,M}为包含各种通信拓扑结构的集合.队列系统的通信拓扑m ∈P定义了车队在任意时刻t的信息流.不同时刻之间,通信拓扑m可能会发生变化,即拓扑切换.切换信号记作σ(t),其中σ(t):R+→P是分段常数函数,作为t时刻对应的通信拓扑索引.切换时刻序列记为τ ∈I≥0,若切换时刻增加,表示通信拓扑发生了切换,即σ(τ1)σ(τ2).

图1示例一种通信拓扑切换:由于通信设备故障或通信网络受到攻击,车辆队列的通信拓扑结构由领车–前车–跟随车(leader-predecessor following,LPF)结构切换为双–前车–跟随车(two-predecessor following,TPF)结构.

图1 通信拓扑切换示例Fig.1 An example of switching topologies

将车辆队列的通信拓扑建模为图G={V,E},其中,V={1,2,···,n}是队列中所有车的集合,而E ⊆V ×V是连接车与车的有序边集.假设车辆队列可切换的有向图包含在有限图集Gm内,其中m∈P.注意,为使队列系统能够稳定运行,切换后的通信拓扑需满足通信距离、通信时延等条件要求,并考虑有限可切换的通信拓扑集合.将Gσ(t)记作t时刻的通信拓扑,对于任意时刻t≥0,有Gσ(t)∈GP.邻接矩阵Aσ(t)表示t时刻的通信拓扑切换下队列的信息流情况,其元素由下式定义:

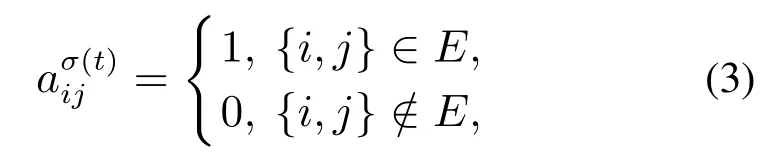
其中:表示在t时刻存在从车辆i到车辆j的信息传递;若无信息传递,则.车辆i的邻居集合记为,其对偶为.上述描述有助于处理下文中的拓扑切换协同控制问题.

定义1[12]如果队列系统(1)对于任意初始状态xi(0)∈Xi,i ∈I[1,n]都能渐近稳定至原点,则称该队列系统具有内部稳定性.

定义2[12]如果队列系统(1)具有内部稳定性,且对于任意初始状态xi(0)∈Xi,i ∈I[1,n]都满足

其中参数γi ∈(0,1),则称队列系统(1)具有弦稳定性.

队列系统内部稳定性是定义在跟踪误差系统原点渐近稳定性的基础上,而队列系统弦稳定性表明前车位置误差波动不会沿着车队反向扩散,即抑制位置误差波动在队列系统中的传播,是队列安全行驶的重要性能[11].因此,队列系统弦稳定性比内部稳定性更加严格.

定义3[26]考虑切换系统z(t+1)=hσ(t)(z(t))及切换信号σ(t),如果存在标量τa,N0≥0满足

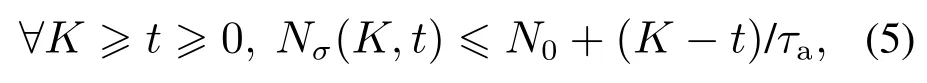
其中Nσ(K,t)是系统在时间间隔[t,K]内的切换次数,则τa称为该系统的平均停留时间.

本文目标是设计分布式MPC策略,使队列系统在通信拓扑切换条件下具有稳定性与弦稳定性,同时满足系统约束和车间保持理想间距dr,其数学描述为

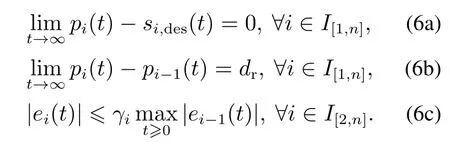
3 分布式MPC控制器设计

结合队列中车辆i和邻居集合中的邻居车辆状态,定义局部滚动时域优化问题.为论述方便,令队列中所有车辆的MPC策略具有相同的预测时域N.在预测时域内分别定义为实际控制量、假设控制量、可行控制量和最优控制量,其中k ∈I[0,N].相应地,和分别为上述控制量作用于系统得到的实际状态量、假设状态量、可行状态量和最优状态变量.假设队列中车辆i能够接收邻居集中的车辆状态信息,也可以向集合中的车辆发送自身的状态信息.邻居集合与其对偶集合中的车辆数目分别记作,满足.

定义车辆i在t ∈I≥0时刻的有限时域最优控制问题

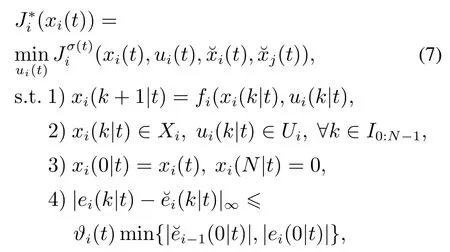
其中:j为集合内车辆的下标;控制序列ui(t)={ui(0|t),···,ui(k|t),···,ui(N−1|t)},xi(k|t),k ∈I[0,N]表示在t时刻对t+k时刻的预测状态量,终端等式约束3)将用于建立队列系统的稳定性[27–28],不等式约束4)将用于建立队列系统的弦稳定性,故称弦稳定约束,ϑi为弦稳定参数,其设计将在后文阐述.由于头车i=1无前车信息输入,即,则约束4)退化为

其中:hi(xi,ui)=‖xi‖Qi+‖ui‖Ri为局部代价函数,描述车辆i的稳定性控制目标;为偏差代价函数,描述车辆i对其假设轨迹的跟踪目标;为车辆i与其邻居车辆的平均协同代价函数,描述车辆队列的协同控制目标.显然,代价函数满足hi(0,0)=0,hsi(0,0)=0,qi(0,0)=0.进一步,权重矩阵Qi ∈R2×2,Ri ∈R,Fi ∈R2×2和Gi∈R2×2为对称正定矩阵,其中F1=G1=0;为优化问题(7)的最优值函数.注意,优化问题(7)是一个非线性非凸的规划问题,如果其存在可行解,则可应用SQP、积极集法等数值算法求解最优解.

下面,给出通信拓扑切换下车辆队列分布式MPC算法描述:

算法1通信拓扑切换下车辆队列分布式MPC算法.

注1初始化步骤2)和3)将保证队列系统在初始时刻的弦稳定性和优化问题(7)的初始可行性[12],即由步骤3)可得如下不等式组:

则车辆i与i −1之间的位置误差关系满足

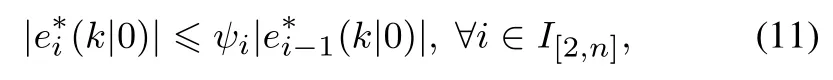
其中:ψ2=(1+ξ2)ς2,ψi=(1+ξi)ςi/(1−ξi−1)ςi−1,∀i ∈I[3,n].选择合适的参数{ξi,ςi}使ψi ∈(0,1),∀i ∈I[2,n].则由定义2可知,该队列系统在初始时刻满足弦稳定性.

4 稳定性分析

为建立车辆队列系统的内部稳定性,累加车辆i ∈I[1,n]的代价函数(8),得

假设1设XN=X1N×X1N×X2N×···×XnN是队列系统的初始状态可行集.假设存在正定函数W1(x),W2(x),W3(x)和常数α1,α2,α3,β1,β2,β3>0,使得对于所有x ∈XN和u ∈U,hΣ(x,u)≥α1W1(x),hsΣ(x)≥α2W2(x)与qsΣ(x)≥α3W3(x),且hΣ(x,u)≤β1W1(x),hsΣ(x)≤β2W2(x),qsΣ(x)≤β3W3(x).

假设1给出了代价函数(8)中各目标子函数的上下界条件.由于代价函数(8)中各子函数为二次型正定目标函数,根据正定函数性质可保证假设1成立.

定理1考虑具有给定通信拓扑σ(t)=m∈P的队列闭环系统(10).如果假设1成立且优化问题(7)在初始时刻t=0存在可行解,则问题(7)在任意时刻t ∈I≥0都是可行的.进一步,如果代价函数(8)中的加权矩阵满足

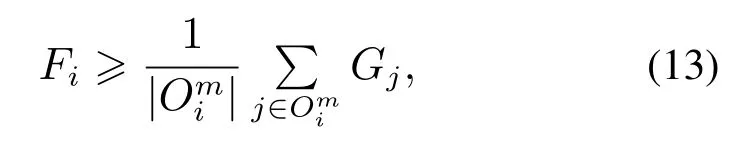
则该闭环系统是关于原点渐近稳定的,即车辆队列系统具有内部稳定性.

证首先证明优化问题(7)的递推可行性.根据t+1时刻假设控制量的构造方式可知,控制序列是该优化问题在t+1时刻的一个可行解,即该优化问题是递推可行的.又优化问题(7)在初始时刻是可行的,故该优化问题在任意t ∈I≥0时刻都是可行的.

现证明队列闭环系统的稳定性.由于优化问题(7)具有递推可行性,在t+1时刻存在一个可行控制序列,满足xi(N|t+1)=0.则对相邻时刻的对应值函数做如下差分运算:

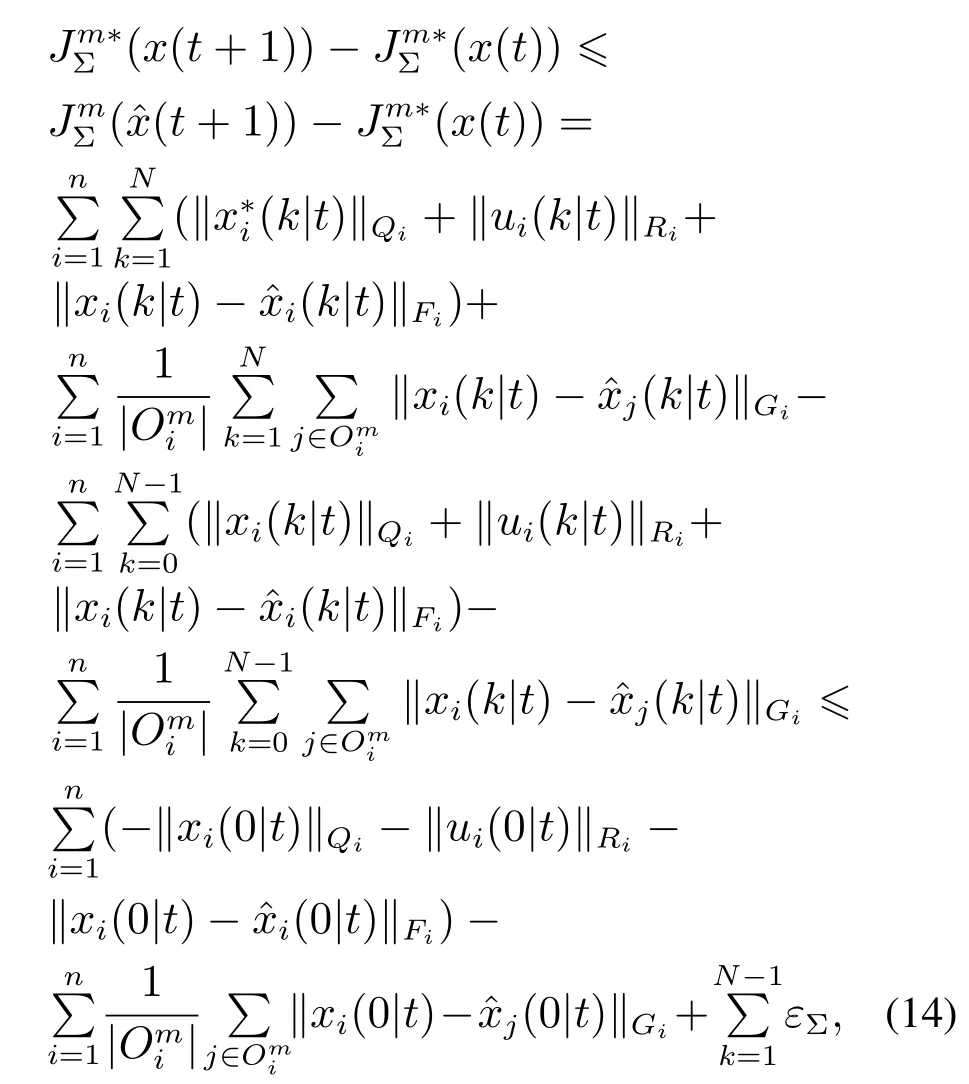
其中

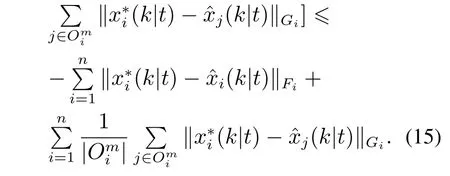
利用向量范数的三角不等式,结合矩阵不等式(13)可得

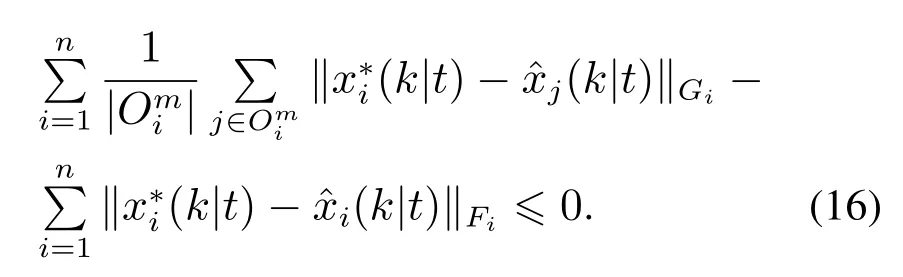
将式(16)代入式(14),可得

注2当求和项ΣGj随着队列规模扩大而增大,不等式(13)右边的平均取值有助于矩阵Qi,Ri,Fi系数的选取.相比于文献[8],平均矩阵不等式(13)可以更灵活地为大型异质队列系统的协同编队控制选择矩阵系数,利于队列系统满足可扩展性.

令τ1和τ2为通信拓扑相继切换的两个不同时刻.不失一般性,令τ1+1<τ2,则基于定理1的结论,车辆队列闭环系统(10)在通信拓扑切换下具有下列稳定性结果.

定理2考虑通信拓扑切换队列闭环系统(10),其中切换行为由切换信号σ(t)描述.令是该系统目标函数(12)的最优值函数.在定理1的条件下,如果存在常数µ≥1和0 ≤λ0≤1,使得如下不等式组:

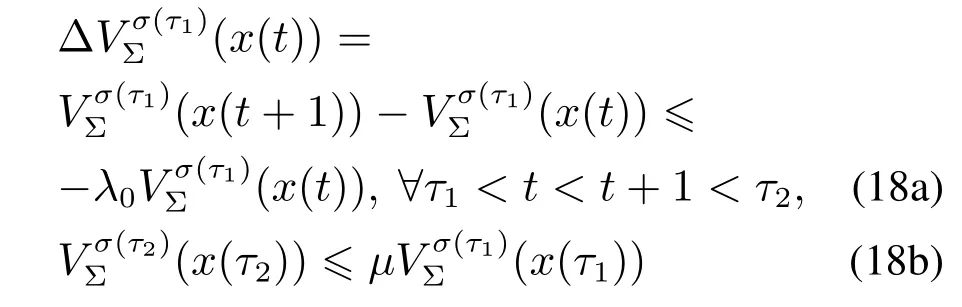
成立,且切换信号σ(t)满足不等式

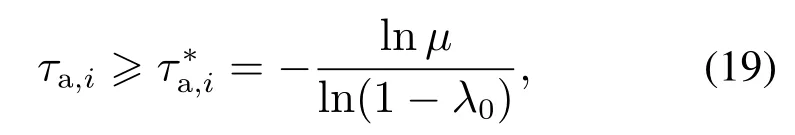
其中:τa,i表示拓扑切换的时间间隔,表示拓扑切换的平均停留时间,则该闭环系统在通信拓扑切换下是关于原点渐近稳定的.

证在满足定理1的条件下,能够保证给定通信拓扑下队列闭环系统的稳定性.下面考虑通信拓扑切换下队列闭环系统(10)的稳定性.

考虑不等式(18a),在相继切换时刻τ1与τ2之间的切换信号满足σ(t)=σ(t+1),则

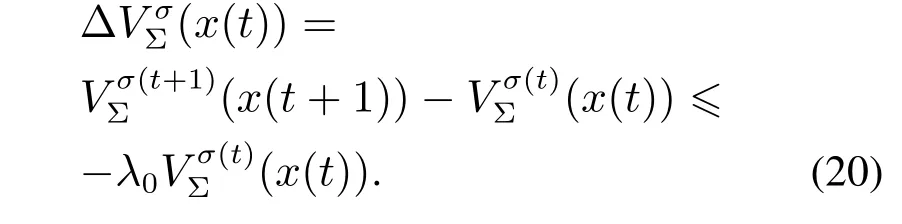
由式(20)可得

对式(21)在[τ,t]上进行递归,可得

若通信拓扑切换次数为Nσ(t,0),结合式(22)与式(18b),得

则根据定义1,通信拓扑切换下队列闭环系统(10)是关于原点渐近稳定的,即队列系统满足内部稳定性.

证毕.

注3定理2表明,队列闭环系统的稳定性依赖于通信拓扑的切换间隔.为计算通信拓扑切换的ADT,需要估计式(18)中的衰减系数λ0和比例系数µ,进而根据式(19)计算保证队列系统满足内部稳定性的平均停留时间.

定理3考虑通信拓扑切换下队列闭环系统(10)及其拓扑切换信号σ.在定理2的假设条件下,如果存在参数θi与ψi ∈(0,1)满足

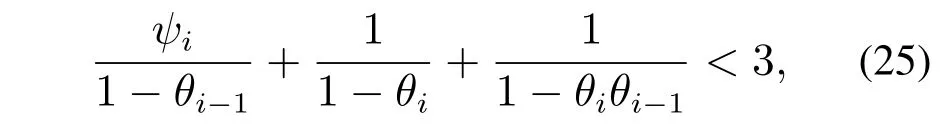
证先由定理2可知,队列闭环系统(10)在通信拓扑切换下具有渐近稳定性.再参考文献[12]定理4的证明思路可直接得到定理3的结论.下面为保证论文结果的完整性,给出该定理的主要证明步骤.

由算法1初始化过程可知,在t=0时刻位置偏差满足

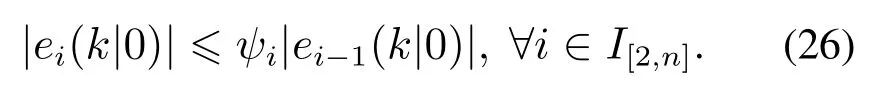
再考虑t=1时刻,结合向量三角不等式与优化问题(7)的约束4),车辆i ∈I[2,n]满足不等式

结合式(31)和式(34),对t ∈I≥0采用数学归纳法可得

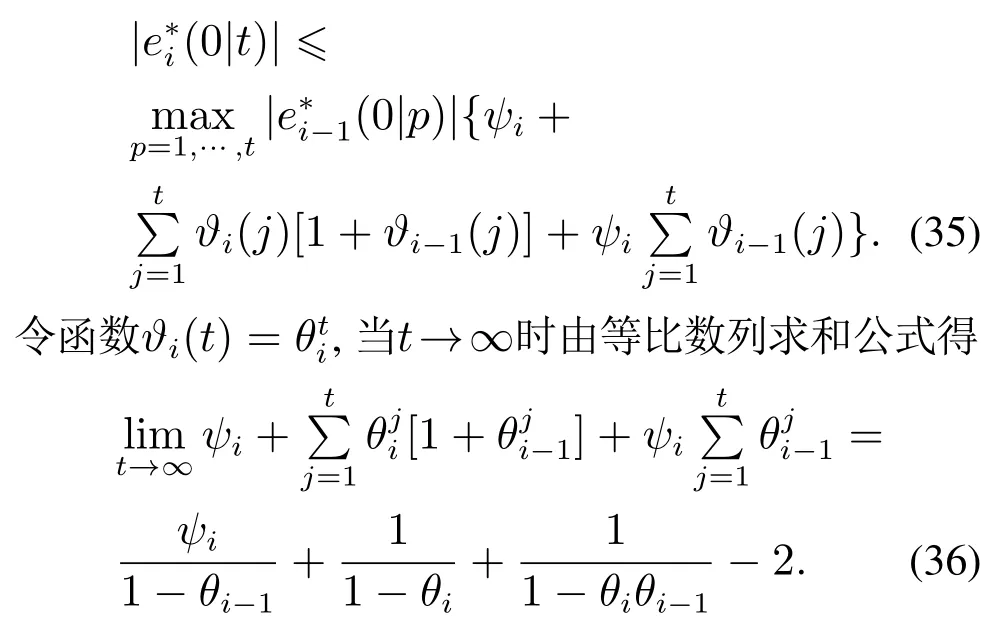
将式(25)和式(36)代入式(35)可得定理3成立.

证毕.

注4尽管定理3的弦稳定性结论与文献[12]相同,但由于文献[12]只考虑通信拓扑不变下车辆队列分布式MPC策略,不涉及切换概念,故两者结论成立的充分条件不同;而文献[21]考虑连续时间非线性系统的切换MPC策略,不涉及分布式控制系统和通信拓扑概念.

5 数值仿真

采用一组同车道行驶的车辆队列验证所提出的分布式MPC策略的有效性.令采样时间Ts=0.5 s,采用如下离散时间非线性模型描述车辆跟踪误差动态系统[12–13]:

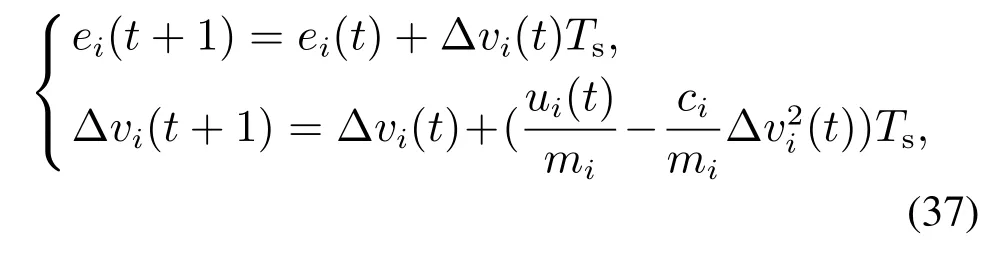
其中:ei(m)为车辆i与参考轨迹之间的相对位置误差,∆vi(m/s)为车辆i与期望速度之间的相对位置误差,控制变量ui(N)为车辆i的驱动力,mi(kg)为车辆i的质量,ci为车辆i的气动阻力系数.设置队列系统的状态约束为|ei|≤10 m和∆vi≤10 m/s,控制输入约束为|ui|≤4500 N.设置各车的动力学参数为mi=1841 kg和ci=0.41.令各车分布式MPC策略中预测时域和控制时域相等,并取为N=6.进一步,设置车辆队列的参考速度为15 m/s(即54 km/h),理想安全间距dr=3 m.假设车联网通信质量满足理想要求,参考信息传输时不存在时延和丢包等情况[29–30].仿真实验首先验证通信拓扑切换的必要性,再验证通信拓扑切换下所提出的分布式MPC策略的有效性.仿真中设计的优化问题将由MATLAB2016 命令函数fmincon调用积极集法(active set method)求解.

5.1 通信拓扑切换的必要性验证

利用三车队列系统验证通信拓扑切换的必要性.设置权值矩阵Qi=I2,Ri=10−4,i=1,2,3和F1=0,G1=0,Fi=I2,Gi=I2,i=2,3,参数ψ1=ψ2=ψ3=0.88,θ1=θ3=0.01,θ2=0.02.在t=0时刻,设置队列系统三车初始状态分别为[e1(0),∆v1(0)]=[1,1],[e2(0),∆v2(0)]=[0.8,1],[e3(0),∆v3(0)]=[0.56,1].设定初始时刻队列系统的通信拓扑采用前车–跟随车拓扑.假设在t=2 s时前车通信信道失效,此时分别考虑通信拓扑切换与非切换两种情况:采用通信拓扑切换,前车通信信道失效后,通信拓扑将从前车–跟随车拓扑切换为领导车–跟随车拓扑,队列系统分布式MPC仿真结果如图2所示;通信拓扑不切换,前车通信信道失效后,车辆将接收不到前车信息,队列系统分布式MPC仿真结果如图3所示.

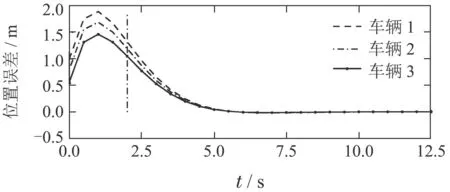
图2 通信拓扑切换下各车相对位置误差Fig.2 Relative position error of each vehicle with changing topologies

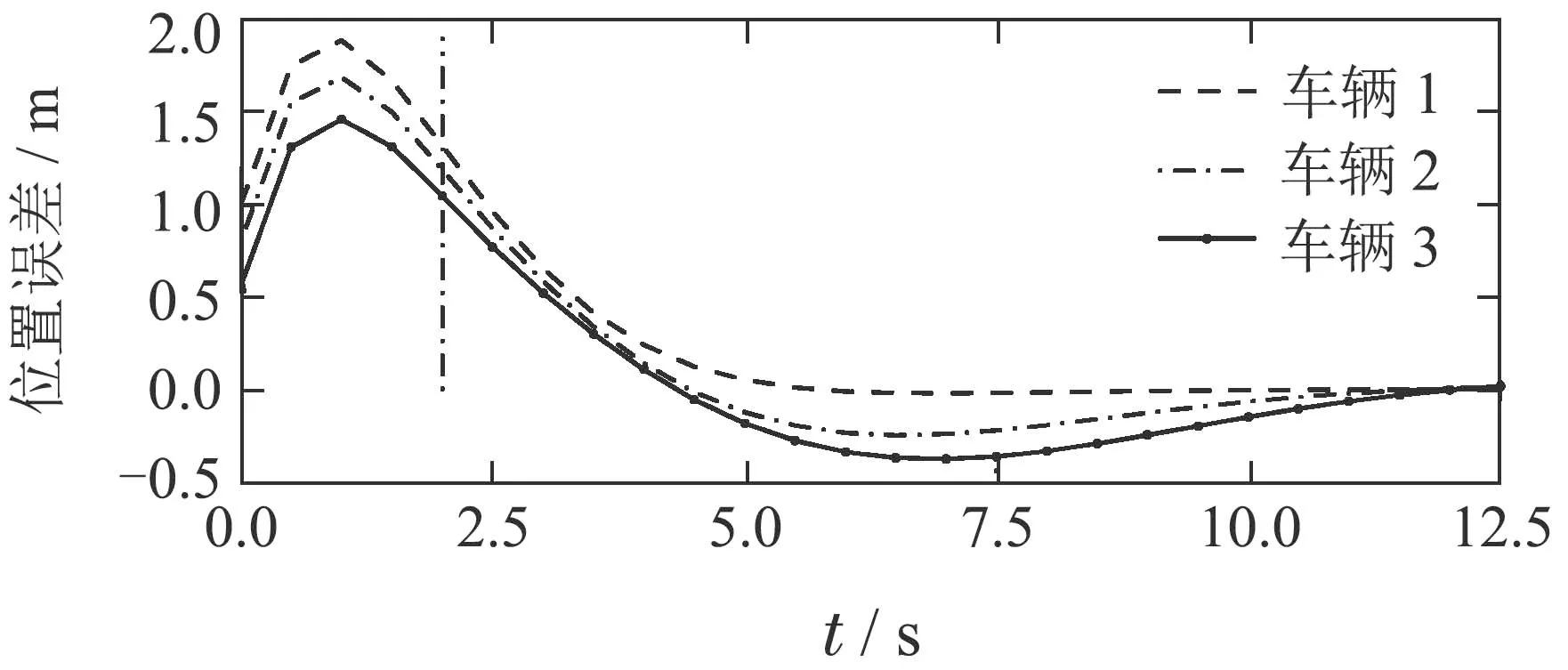
图3 无通信拓扑切换下各车相对位置误差Fig.3 Relative position error of each vehicle without changing topologies

从图2与图3可以看出,两种情况下队列系统都可以到达期望状态而不发生任何碰撞.考虑通信拓扑切换下分布式MPC策略的控制效果如图2所示,在时刻t=2 s时,虽然车队中车辆丢失了前车通信信道,但是车队的通信拓扑及时从前车–跟随车拓扑切换为领导车–跟随车拓扑,从而保证了车队的内部稳定性与弦稳定性.但通信拓扑不切换下分布式MPC策略的控制效果如图3所示,由于前车信道失效后车队没有及时地切换通信拓扑,队列系统由分布式控制退化为分散式控制,即后车无法利用邻居车辆的信息,导致车辆队列虽然能够保证内部稳定性,但是无法保证弦稳定性.结果表明,当队列系统出现通信故障等问题时,及时切换通信拓扑是必要的,但由切换控制理论可知,通信拓扑频繁切换可能对队列系统的稳定性造成不利影响.对此,实验2将利用切换控制理论中的平均停留时间概念,计算保证车辆队列系统内部稳定性和弦稳定性的通信拓扑切换容许最大频率.

5.2 拓扑切换下队列控制

考虑由7车组成的队列系统在通信拓扑切换下的队列控制问题,相应的通信拓扑切换如图1所示,即车辆队列的通信拓扑结构由LPF结构切换为TPF结构.注意,这两种拓扑结构在车辆队列系统中具有代表性,已广泛用于车辆队列控制的研究[1–5].分别定义如下二次型函数和表示与拓扑LPF和TPF相对应的车辆i ∈I[1,7]的代价函数:

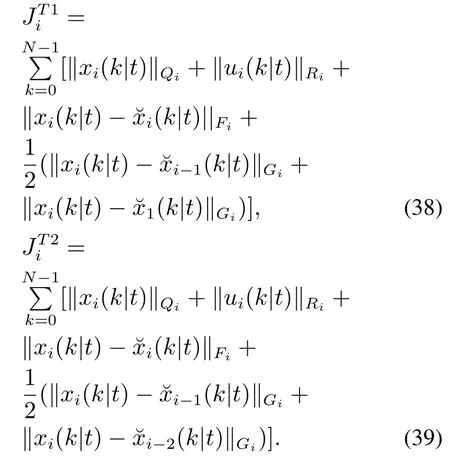
为满足假设1与定理1条件,对分布式MPC控制器参数设置如下:对车辆i∈I[1,7],令Qi=I2,Ri=10−4,Fi=0.1I2;对车辆i=1设置G1=0;对车辆i ∈I[2,7]有Gi=0.1I2;系数α1=β1=1.0,α2=α3=β2=β3=0.1.考虑由LPF拓扑向TPF拓扑切换下队列闭环系统的稳定性,采用文献[21,31]方法估计λ0=0.0279和µ=1.1667.根据式(19)计算切换信号平均停留时间=5.4686,因此队列系统的通信拓扑切换信号σ(t)的切换间隔应满足.令切换信号σ(t)=0表示LPF通信拓扑;σ(t)=1表示TPF通信拓扑.根据平均停留时间条件,为保证切换通信拓扑下车辆队列系统的稳定性,采用如图4所示的通信拓扑切换信号σ(t).进一步,为满足定理3中的弦稳定约束条件,设置参数ψi=0.97,i ∈I[1,7];θi=θ1=0.01,i ∈I[3,7],θ2=0.02.

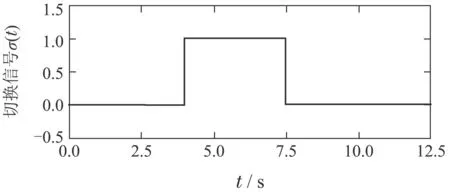
图4 通信拓扑切换信号Fig.4 Switching signal of communication topologies

在仿真中,考虑如下行驶工况:在时间段t ∈[0,2.5]s内,车辆队列稳定行驶,在时刻t=2.5 s时,控制中心广播队列参考速度vdes从26 m/s降为25 m/s,等价于车辆队列的新初始可行状态变为[ei(0),∆vi(0)]=[0,−1],i ∈I[1,7],即该队列中各车都处于其参考位置,但是初始速度大于其参考速度.运行本文提出的分布式MPC策略,对应数值仿真结果如图5–7所示,其中图5–7分别表示队列中各车辆相应的相对位置误差、速度误差和控制量的变化曲线.

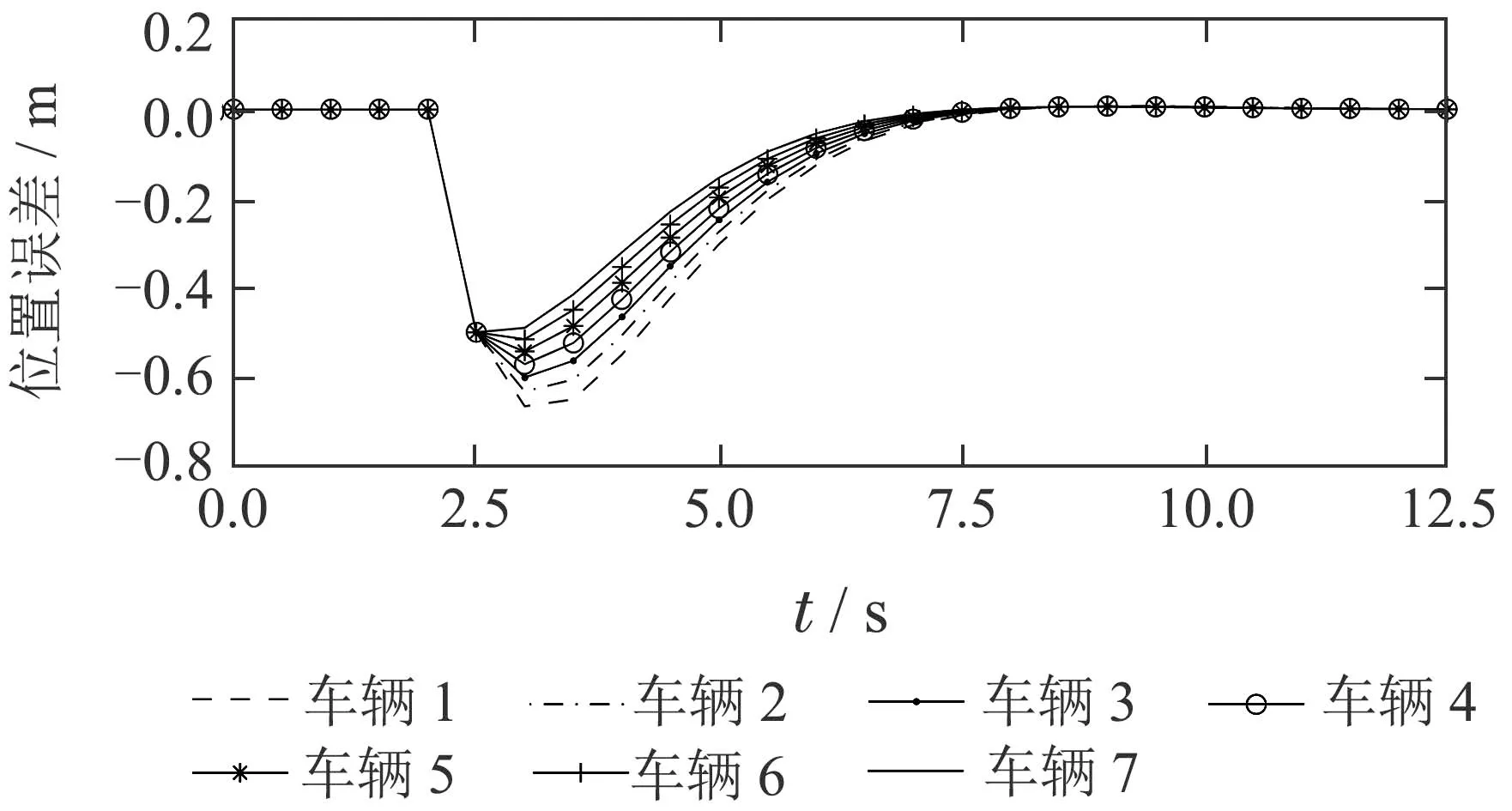
图5 队列中各车的相对位置误差Fig.5 Relative position errors of each vehicle in the platoon

由图5–7分析可知,在本文分布式MPC控制器作用下,该车辆队列闭环系统在每个时刻都满足状态约束和控制量约束.进一步,分析图5和图6可知,在t=4 s时刻与t=7.5 s时刻,该车辆队列的通信拓扑发生了两次切换,但由于拓扑切换时间间隔满足平均停留时间条件,队列闭环系统仍是关于原点渐近稳定的.从图5中还可以看出,即使队列系统存在通信拓扑切换,队列中所有车辆的位置误差在任意时刻仍满足弦稳定性条件(6c).同时分析图6可知,当参考速度发生变化后,该车辆队列系统在分布式MPC策略作用下能够快速跟踪新的参考速度,进而实现快速协同队列控制目标,而图7则表明,该车辆队列系统的分布式MPC优化问题在任意时刻都存在控制序列解.

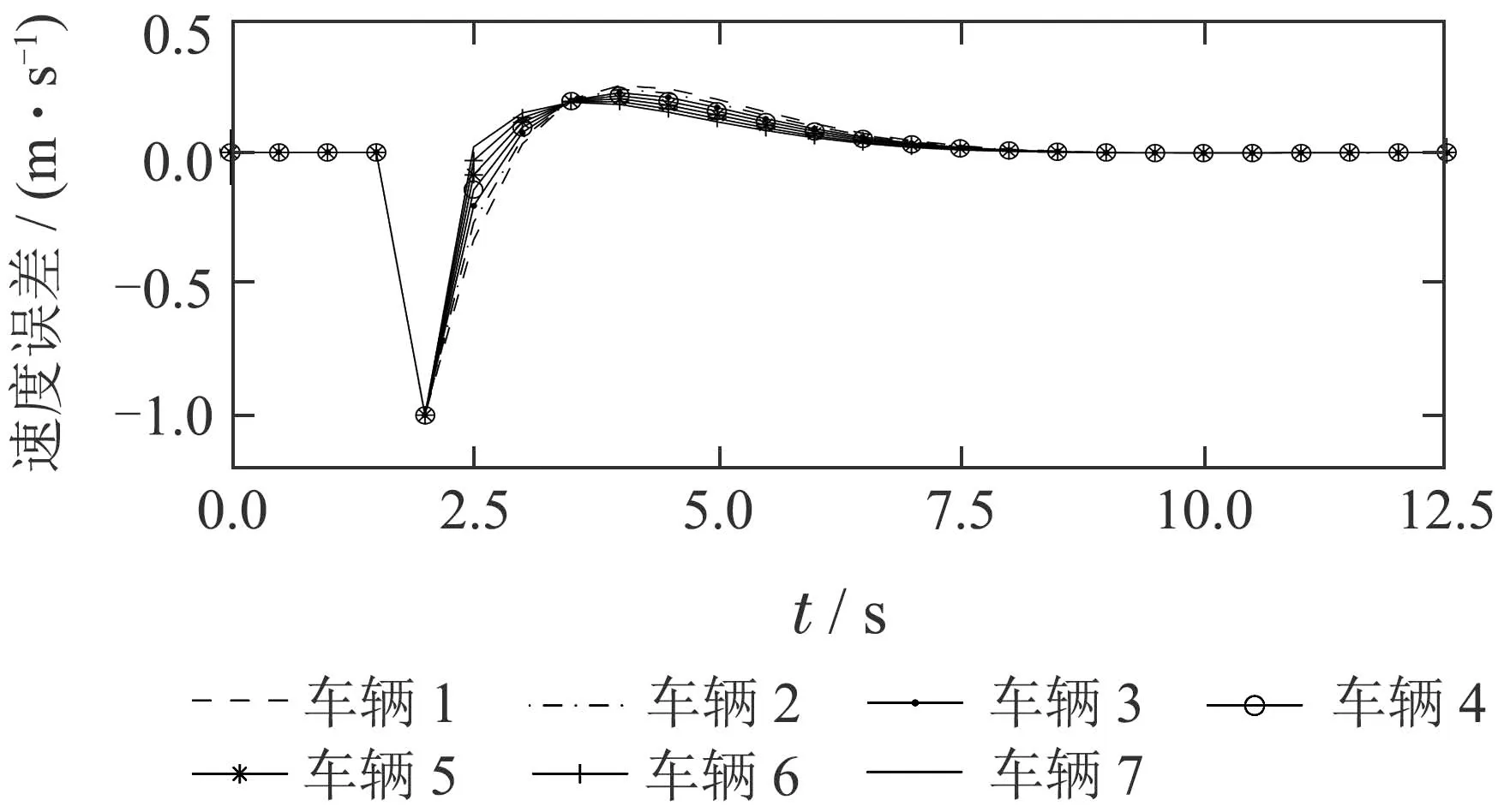
图6 队列中各车的速度误差Fig.6 Velocity errors of each vehicle in the platoon

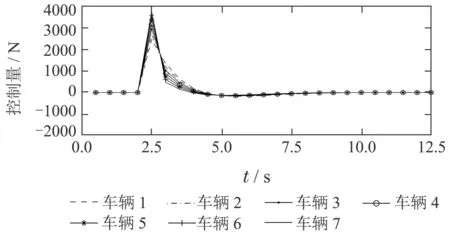
图7 队列中各车的控制量Fig.7 Control profiles of each vehicle in the platoon

为进一步验证本文分布式MPC策略对通信拓扑切换下车辆队列控制的有效性,比较文献[12]分布式MPC 策略的运行结果.为便于书写,记本文分布式MPC策略为(S–DMPC),文献[12]分布式MPC策略为(T–DMPC).采用队列系统各车辆的相对位置误差标准差[24]和速度误差标准差作为控制效果衡量指标,标准差越小表明控制效果越好.当车辆队列的通信拓扑由LPF结构切换为TPF结构,S–DMPC 和T–DMPC控制下的各车位置误差标准差和速度误差标准差如图8和图9所示,其中:横坐标表示第i辆车,纵坐标表示标准差;“∗”对应S–DMPC结果,“o”对应T–DMPC结果.分析图8和图9的标准差可知,对通信拓扑切换下车辆队列系统的控制,S–DMPC在相对位置误差标准差和速度误差标准差方面都优于T–DMPC的结果,即本文分布式MPC策略在车辆队列系统通信拓扑切换下的控制效果较现有分布式MPC策略有显著提升.

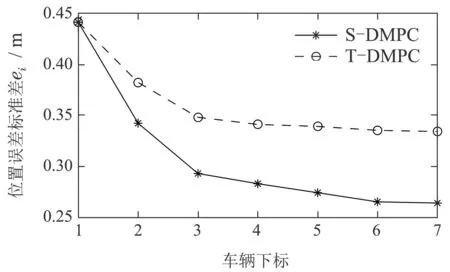
图8 队列中各车的位置误差标准差Fig.8 Standard deviation of position error of each vehicle

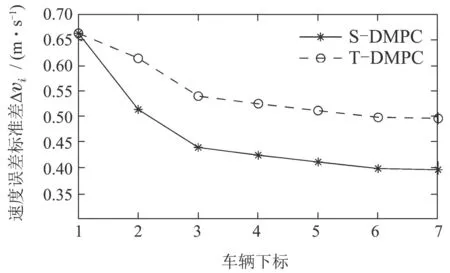
图9 队列中各车的速度误差标准差Fig.9 Standard deviation of velocity error of each vehicle

综上可知,本文所提出的分布式MPC策略能够保证通信拓扑发生切换下闭环队列系统的稳定性和弦稳定性,同时能够避免编队过程中发生车辆碰撞,使所有车辆都能够快速跟踪参考轨迹和期望速度,实现协同队列控制目标.

6 结语

针对通信拓扑切换下异质车辆队列系统的非线性协同队列控制问题,提出了一种保证队列系统稳定性与弦稳定性的分布式MPC策略.采用时间相关图函数描述动态通信拓扑切换过程,据此接收邻居集合内车辆的状态信息,定义描述车辆之间协同编队的耦合代价函数.再将平均协同代价函数引入滚动时域优化问题,结合平均停留时间概念与切换系统Lyapunov稳定性理论,建立关于加权矩阵和值函数相关的队列系统稳定性与弦稳定性充分条件.仿真结果验证了本文分布式MPC策略的有效性.在本文结果基础上,后续将研究车辆队列系统不等式终端约束分布式MPC策略及其高效计算方法.