通讯受限条件下的机器人编队算法
罗家祥,关振峰,刘海明,蔡 鹤,高焕丽,黄 杰
(华南理工大学自动化科学与工程学院,广东广州 510640)
1 引言
近年来,集群运动研究受到各领域研究者的广泛关注,探索集群中个体的运动模型是集群运动研究的核心问题.自然界广泛存在大量单个个体通过局部相互作用自行聚集成特定形状的例子[1].例如鸟群可以通过与相邻个体交互形成编队[2].受此启发,基于个体运动规则的机器人编队研究成为集群运动研究的热点[3].
机器人编队任务是指机器人个体在仅存在局部交互的条件下整个群体能够形成并维持给定队形[4–5].机器人编队设计方法主要有:领航–跟随法[6–8]、基于行为法[9–10]、虚拟结构法[11–12].其中领航–跟随法通过设置领航者,让跟随者跟随领航者以形成队形,例如:Du等[13]提出了一种基于有限时间观测器的分布式领航–跟随控制策略,该策略首先利用能在有限时间内收敛的观测器估计领航者有限时间内的状态,并基于上述估计设计能在有限时间内跟随领航者状态的有限时间控制器,该方法能够很好的实现对领航者将来位置的估计和跟踪.虽然领航–跟随法在实现上最简单但是需要确定固定领航者;基于行为法对机器人各种状态分别确定行为,例如:Xu等[14]提出了基于分类的初始编队位置搜索方式来实现初始编队的形成,接着通过基于行为法进行编队移动和避障等操作,但是该方法需要一个主控单元来完成初始编队的计算任务无法以分布式控制的方式完成整个编队任务;虚拟结构法将所有成员视为一个刚性结构体以刚体形状作为编队形状,其优点是能够严格保持队形,但是灵活性不足并且还存在计算量大、对通讯要求严格等问题,例如:Fu等[15]提出了机器人通过与虚拟领导者和相邻两个机器人保持一定距离以形成编队.除上述方法外还有Elkilany等[16]提出了一种优化势场法,该方法队形是通过保持与相邻个体的特定距离来形成特定队形的,还加入了人工神经网络在线优化势能参数以解决传统势场法问题,最终成功完成避障、编队保持、追踪目标3个任务.
以上方法通常假设通信能力不受限,个体可获得其他个体的所有信息,能够实现有领导者的编队控制.但在实际情况下,随着群体数量的增加,通讯负载将会增大,有领导者的编队控制可能会因为通信能力不足而无法快速形成队形.如,文献[15]通过机器人参考相邻两机器人和虚拟领导者的位置和方位形成线形编队,可快速收敛到一条曲线上,但在通信受限条件下,由于个体无法获得全局信息便无法构造虚拟领导者,机器人只能根据相邻机器人状态调整位置,这样导致其最后收敛到设定线形的时间长;文献[16]提出机器人利用与相邻机器人保持一定距离和方位的规则来形成编队,只有当每个机器人个体都跟随同一个方向上距离最近的相邻机器人才能形成线形编队,这就需要从跟随队首的机器人个体开始,依次调整,这种调整方式速度慢,机器人个体调整路径大,能量消耗大.
本文针对通讯能力受限的线形编队问题,在文献[15–16]的基础上,提出了基于位置预测的无领导者线形编队算法,具体方法是:机器人个体在从初始位置开始大幅调整时,向相邻两机器人个体的中点移动,当机器人个体调整到近线形状态后,机器人个体根据当前速度预测调整方向,结合相邻两机器人个体相对位置选择跟随机器人个体,最终实现线形编队.同时,算法充分考虑了防碰撞机制和避障机制,使得群体可在有障碍物条件下完成编队.对比文献[15],本文不需要构建虚拟领导者,可根据机器人个体状态选择跟随对象;对比文献[16],本文在队形调整初始阶段利用了相邻两体的中心快速调整,而不是在所有时刻单一跟随某个机器人个体.本文所提出方法能够在通信受限条件下快速形成编队.
2 问题描述
2.1 移动机器人模型
设本文总共有k1个移动机器人形成编队,所有移动机器人集合R={ri|i=1,2,···,k1},pi[t]=(xi[t]yi[t])T为移动机器人ri在t时刻的位置,pi[t]∈R2,vi[t]=(vxi[t]vyi[t])T为移动机器人ri在t时刻的设定速度,则移动机器人ri的运动学模型如下所示:

其中:设机器人移动的最大速度vmax,并使得式(1)中的vi[t]满足‖vi[t]‖2≤vmax,该模型假设移动机器人每一时刻移动机器人的速度都为设定速度.
2.2 坐标系与状态设置
本节通过绝对的世界坐标系来建立期望速度坐标系以及编队坐标系两个相对坐标系.移动机器人ri和rj之间的向量在世界坐标系中表示为:pji[t]=pj[t]−pi[t].另有k2个固定圆形障碍物,所有障碍物集合O={om|m=1,2,···,k2},om的圆心在世界坐标系中的坐标为pom[t]∈R2,移动机器人ri和障碍物om之间的向量在世界坐标系中表示为:pomi[t]=pom[t]−pi[t].

上述坐标系设置如图1所示.
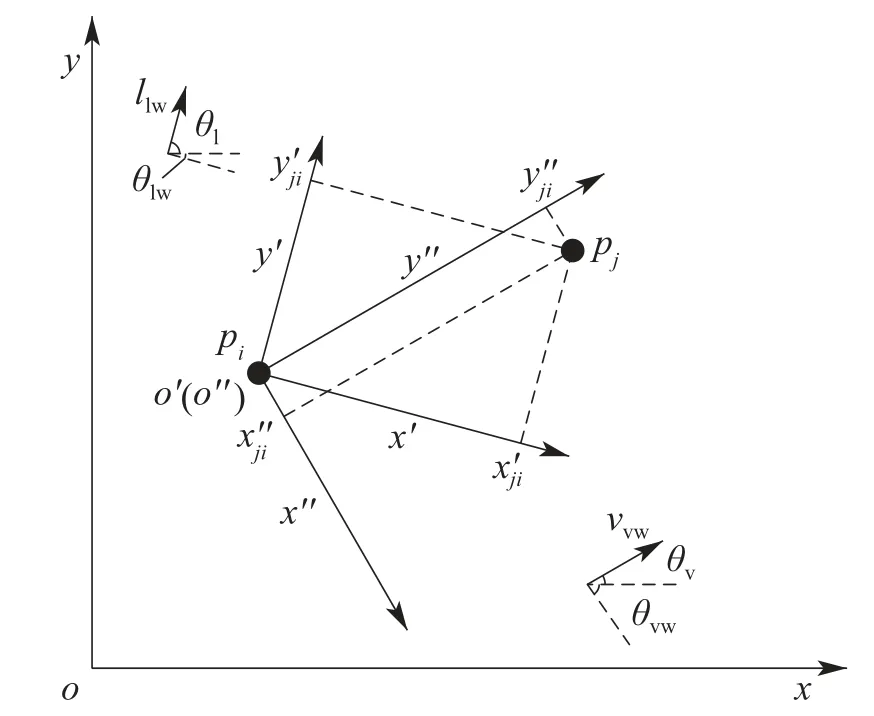
图1 坐标系设置Fig.1 Coordinate system setting
世界坐标系下的相对向量可以根据下式转化为编队坐标系下的相对向量:

同理,世界坐标系下的相对向量转化方式为

2.3 任务描述
本文算法任务为使得随机初始位置的机器人形成编队,并以vlw的速度行进.
对于队中状态的移动机器人来说,距离期望位置为其两个相关联机器人rij1与rij2之间连线的中点,并且平行四边形对角线相互平分,那么rm与期望位置的偏差如下式所示:
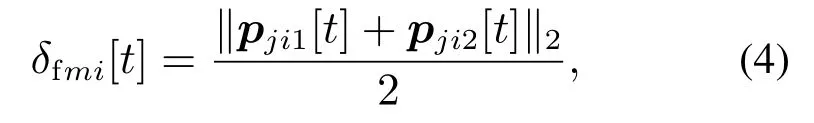
其中:pji1[t]=pij1[t]−pi[t],pji2[t]=pij2[t]−pi[t].
对于队首状态的移动机器人来说,期望位置偏差与rij2和队形方向有关,将与期望位置的偏差分为与队形方向同方向的δyhi[t]和与队形方向垂直方向的δxhi[t].

其中dl为给定机器人之间的距离.
同理,对于队尾状态的移动机器人来说,期望位置偏差与rij1和队形方向有关,将与期望位置的偏差分为与队形方向同方向的δyti[t]和与队形方向垂直方向的δxti[t]:
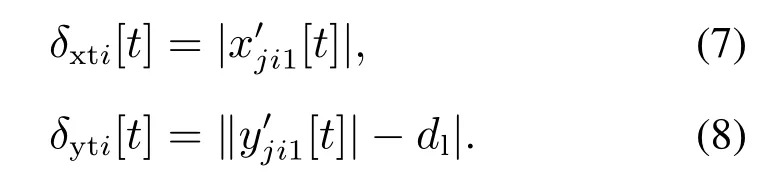
而编队任务的目标是控制移动机器人ri使得δfmi,δxhi,δyhi,δxti,δyti趋近于0,若上述5个偏差最终都变为0,那么整个机器人编队会最终变为设定线形编队,并且相邻机器人之间的距离也会变为设定值.
3 算法设计
本文设计算法中移动机器人有以下3种行为:
1) 位置预测;
2) 编队行进;
3) 避障.
以上3种行为的优先级由上而下逐渐升高.
其中,编队行进行为的目的是使机器人群体在以给定速度前进时逐渐形成线形编队.位置预测是在机器人形成编队时根据自身速度信息以及相邻机器人信息调整自身编队策略以达到快速形成线形编队目的的行为.避障行为是为了避免机器人在行进过程中撞上障碍物.由于位置预测行为表现在编队行进过程中,不直接影响速度,因此设计编队行进以及避障两种行为下ri的给定速度如式(9).
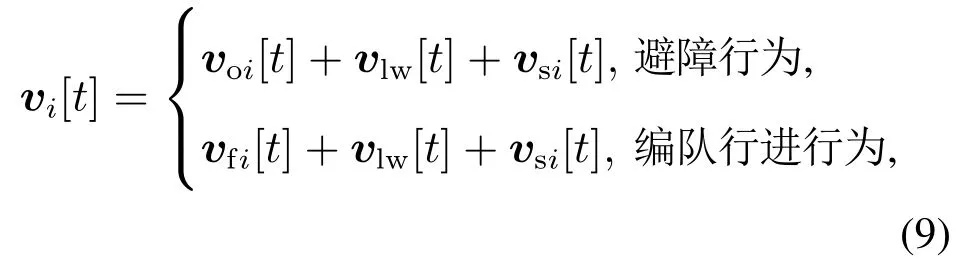
其中:vlw[t]为给定的群体期望速度;vsi[t]为防碰撞期望速度;voi[t],vfi[t]分别为避障期望速度分量、编队期望速度分量.其中vfi[t],vsi[t],voi[t]将分别在下文讨论.
3.1 编队行进
本文所采取的编队方式与文献[16]所采取的势场法方法类似,都是根据周围机器人位置对自己有力的作用,并通过力所产生的势场来形成编队.但是,本文的前提条件更加严格,机器人只能获取其相邻最近机器人rij1和rij2的信息,无法获得所有机器人个体的信息,且整个群体是无领导者的,因此单个机器人个体既无法通过群体信息来确认自己需要到达的位置,也无法通过与领导者保持特定的相对位置来形成编队.单个机器人个体只能通过相邻机器人个体的位置信息以及自身速度信息来自行决策,文献[16]中采取的单边跟随方法,即只与rij1或rij2保持特定角度与距离;文献[15]中采取的双边跟随方法,该方法充分利用所有相邻机器人位置信息,即以rij1和rij2的中点为期望位置,通过相互作用不断调整机器人个体位置最终形成线形.
上述两种方法各有优缺点:单边跟随的方法能够使群体比较快地收敛到直线编队,但是其调整过程可能会因为跟随对象同时在调整导致能量消耗增加;而双边跟随的方法由于同时参考更多信息能够减少能量消耗,但由于同时参考的信息过多导致在群体以及形成线之后调整到设定的角度和间距的耗时过长.
针对上述两种方法的优缺点,本文的编队形成方法结合单边跟随和双边跟随策略,通过预测机制调整其采取策略,在需要大幅调整时采取双边跟随策略,而在已经调整成为线形的时候预测其所处位置,并以期望位置的邻居信息为参考使用单边跟随的方法,减少编队形成消耗的时间.
编队期望速度分量是使移动机器人群体趋向于形成设定的线形.编队期望速度分量定义如下:
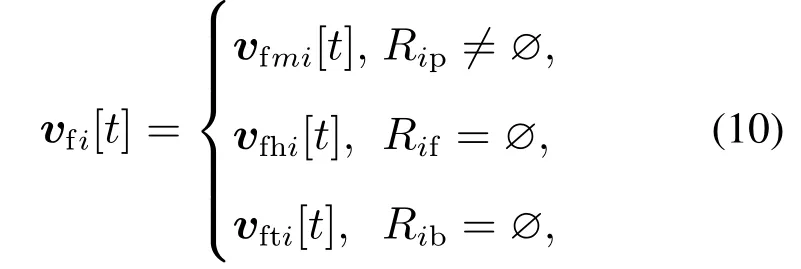
其中:Rip≠∅表示队中状态,Rif=∅表示队首状态,Rib=∅表示队尾状态.该式表示当ri为队中状态时编队期望速度取vfmi[t],为队首状态时编队期望速度取vfhi[t],为队尾状态时编队期望速度取vfti[t].
3.1.1 队中状态编队行进与位置预测
由于位置预测行为是在队中状态编队行进时通过切换跟随策略来达到更快形成给定队形目的的行为,因此在本小节中同时介绍队中状态编队行进与位置预测.
编队行进行为需要将某个机器人ri与其关联机器人rij1和rij2的相对位置pji1[t]和pji2[t]分别分解为ppji1[t]和pvji1[t]以及ppji2[t]和pvji2[t].以pji2[t]为例,分解如图2所示.

图2 pji2[t]分解示意图Fig.2 Decomposition diagram of pji2[t]
以ppji2[t]和pvji2[t]为例,其具体计算公式如下:
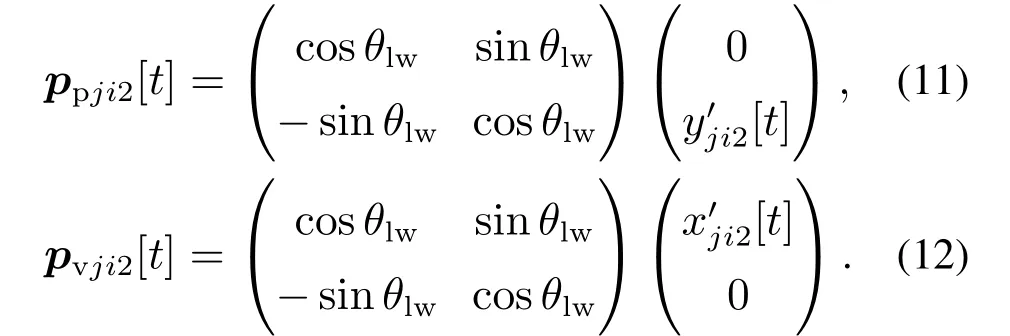
基于上述分量分解结果,vfmi[t]设计如下:
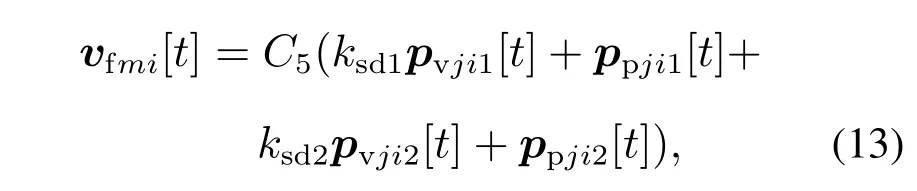
其中:C5为常数,ksd1和ksd2为取值为0或1的参数,该参数由位置预测行为确定,且不采取位置预测行为时ksd1和ksd2都为1.采取位置预测行为时由于ksd1和ksd2只能取0和1,其影响的是期望队形方向水平方向的分量,在队形形成过程中,若该参数为0表示机器人个体不使用该方向关联机器人的位置信息,反之,若该参数为1表示机器人个体将该方向关联机器人的位置信息纳入考虑.
位置预测行为是将机器人可以获得的自身速度信息,以及关联机器人信息综合起来判断机器人处在期望队形方向的左侧还是右侧,接着根据关联机器人在机器人个体的左边或者右边决定跟随关系.
上文已经假设能够通过传感器获取关联机器人的位置信息,算法还需要机器人当前速度信息,为防止由于误差或者突然调整导致速度信息波动较大,采取一定时间段内的速度进行加权平均,并计算这一时间段之内速度的方差,该方差能够反映这一段时间内速度的变化情况,据此能判断机器人是否正在大幅调整,便能将其作为机器人位置的预测依据.队形调整平均速度和方差的表达式如下:
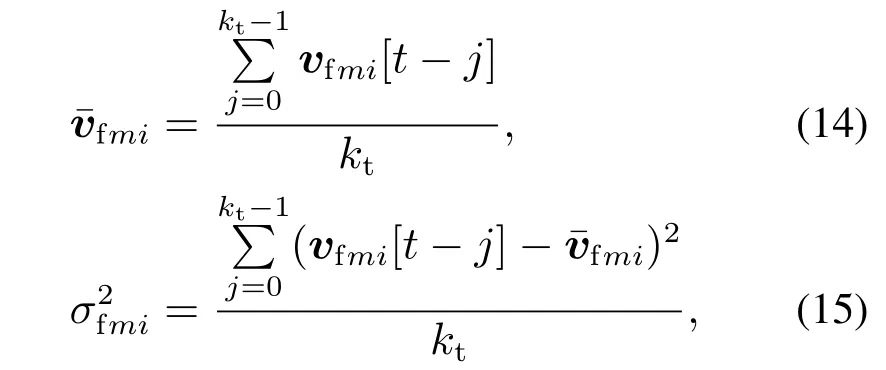
其中kt表示采取的时间段长度,即求平均的时刻的个数.


3.1.2 队首–队尾状态编队行进
由前文可知,当移动机器人ri处在队首–队尾状态时,仅有一个与其相关联的机器人rij2(rij1).由于本文需要控制一条直线的角度和长度,于是就需要控制每个相邻移动机器人相对位置向量角度θl和距离dl.而这角度和距离就只需要处在队首–队尾状态的机器人来控制,最终形成本文所设定的队形.
该状态的编队期望速度设计如下:
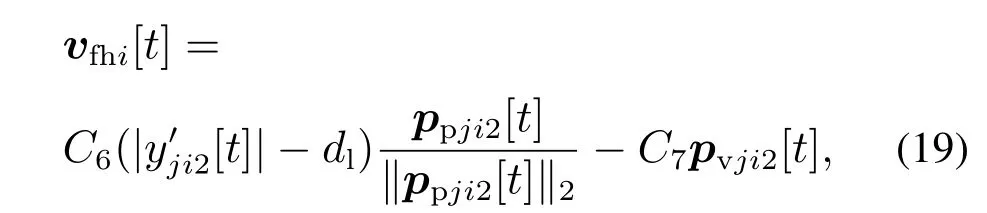
其中C6和C7为常数.
编队期望速度是通过将设定角度θl和相对距离dl转化为坐标系x′o′y′,再通过坐标系的x′轴和y′轴的值来控制的.
vfti[t]为处在rh移动机器人ri的编队期望速度与vfhi[t]类似.
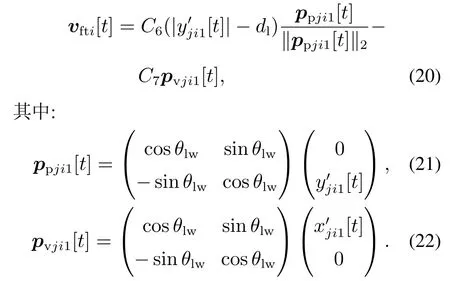
3.2 防碰撞机制及避障机制
为了防止碰撞,本文采取了防碰撞机制使机器人与机器人或者机器人与障碍之间距离小于一个安全值时产生一个反向的斥力,将机器人推离即将撞上的物体;而为了让机器人提前躲避障碍物本文设计了避障行为的控制方式,使得机器人在进入障碍物的避障距离后能够提前动作绕开障碍物.
上述的防碰撞和避障分别是在即将撞上物体和以及感知到障碍物时采取的避免碰撞的措施,因此其作用的时间不同.防碰撞需要在移动机器人移动的任何时候起作用,而避障作为一种提前躲避障碍物的行为,只需要在移动机器人进入到障碍物的避障范围内后才会起作用.
对于移动机器人ri来说,当其检测到机器人rj与其相对距离小于dsr时,其防碰撞期望速度vsi[t]是背离rj的,且距离越近该速度大小越大,反之,若没有其他机器人进入安全距离,则其该项的防碰撞期望速度为零,防碰撞期望速度vsi[t]设计如下:
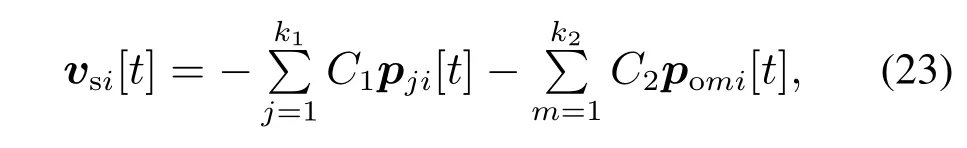
其中C1和C2为常数.
假设障碍物相互之间存在空隙.当移动机器人检测到其与任意一个障碍物之间的距离小于避障距离do时,移动机器人为了避开障碍物便会采取避障机制.在避障过程中,移动机器人会在保持给定期望速度的基础上,根据与障碍物的相对位置加上一个与期望速度垂直的避障速度分量.

式中:C3为常数,domi[t]=‖pomi[t]‖2表示移动机器人ri与障碍物om之间的距离.
voi[t]在时为0是由于此时对于移动机器人前进方向来说障碍物位于后方,若机器人保持移动方向便不可能与障碍物产生碰撞,并且该分量也会对机器人避开后续障碍物产生影响,因此此时无需施加避障分量,但若此时切换至编队行为,便可能使得机器人产生与前进方向的合速度,有与障碍物产生碰撞的风险,综合上述原因,在时使得voi[t]为0可以有效避开障碍物,且保持避障行为继续前进直至机器人与障碍物间的距离大于do.
4 稳定性分析
本文参考文献[17]所采用的方法来进行稳定性分析.
下面将分别对上文所描述的队中编队行进以及队首–队尾编队行进来进行稳定性分析.
本文算法在最后接近稳定状态时采取双边跟随策略,因此,只需要考虑双边跟随算法的稳定性即可.
由于只考虑编队稳定性,因此编队行进行为的编队期望速度稳定,队中状态的编队期望速度如式(13)所示,将其转化为标量
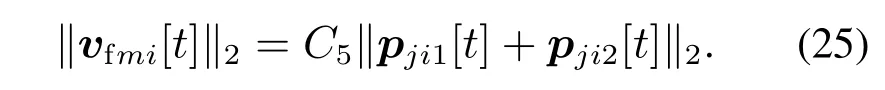
当δfmi[t]→0时,每个点都和相关联的两个点位于同一条直线上,并且该点平分关联两点相连所形成的线段,此时能够形成稳定编队,偏差如下式表示:
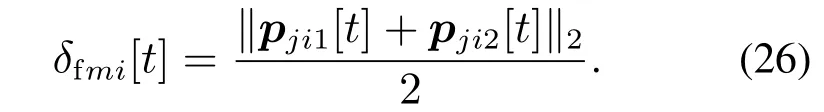
根据式(25)–(26)可得rm的编队偏差为
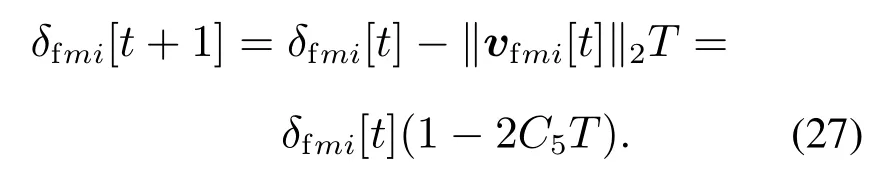
取Lyapunov函数可得V(δfmi[t])为

易得V(δfmi[t])正定,且V(0)=0,并且,有

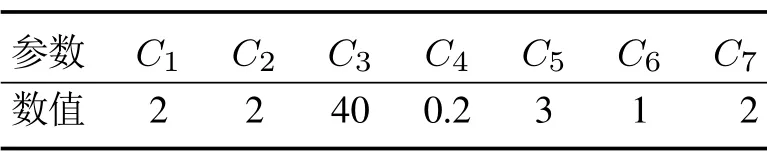
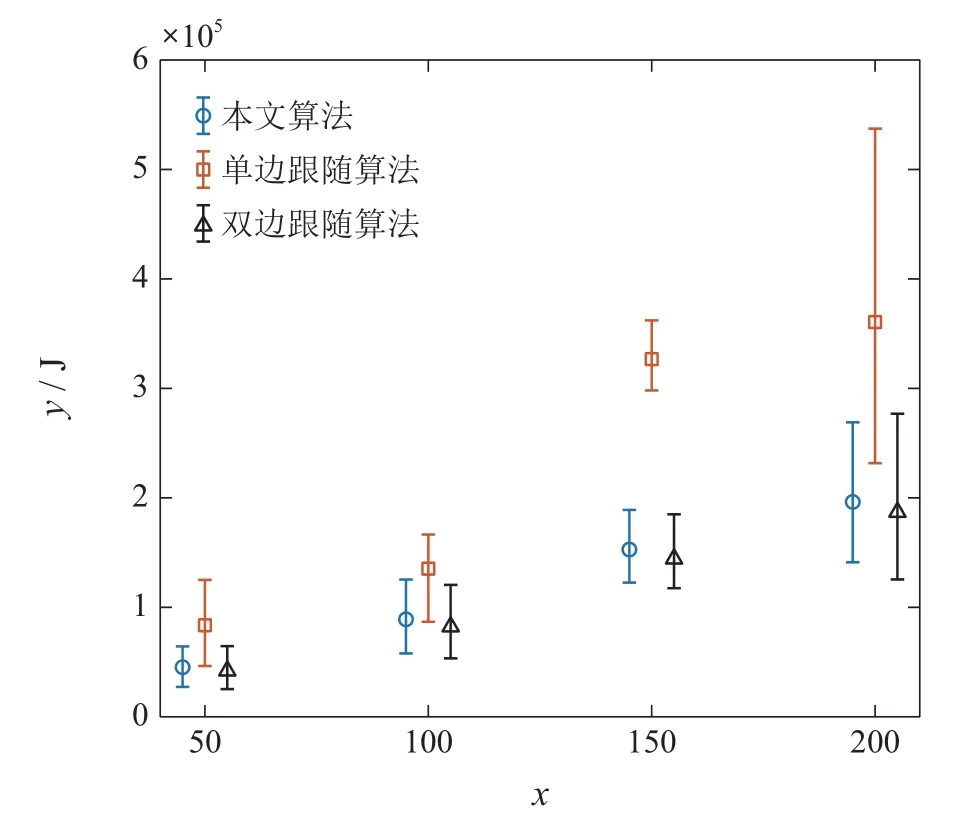
易求得当(|1−2C5T|−1)<0时ΔV(δfmi[t])负定,此时0 由于队中编队行进行为稳定,那么所有队中状态机器人最终都会与相关联的rij1和rij2处于同一条直线上. 用同样的方法对队首和队尾状态编队行进行为进行稳定性分析.由于队首和队尾状态编队期望速度vfhi[t]和vfti[t]几乎相同,因此只需若vfhi[t]稳定,便可推出vfti[t]稳定. 由于编队期望速度vfhi[t]是由ppji2[t],pvji2[t]两个相互垂直的分量计算的,因此,将期望位置偏差也分为与ppji2[t]同方向的δyhi[t]和与pvji2[t]同方向的δxhi[t].根据前文所述易得 此处δxhi[t]和δyhi[t]都取绝对值是由于其速度分量都是朝着使δ的值减小的方向的所以只需要考虑距离的标量,所以位置偏差只为正值. 可将式(19)分解为相互垂直的两个向量vpji2[t]和vvji2[t] 易得,在0 队首和队尾编队行进行为稳定会使得队首和队尾状态机器人分别与关联机器人形成直线,并且直线的角度和两机器人之间的间距满足编队设定值. 用Python进行算法仿真,参数设置如表1所示,给定值如表2所示. 表1 参数设置Table 1 Parameter setting 表2 给定值Table 2 Given value 为了分别展示算法的避障能力和在无障碍环境中编队组织能力,下面所展示的仿真实验分别设置了有障碍少量机器人(图3)和无障碍大量机器人(图4–6)的两种场景.其中,图4–6所用的参数均相同,机器人的生成采用相同的随机种子,这样使得机器人生成位置也相同,图4采用本文算法,图5采用文献[16]中使用的单边跟随算法,下文简称单边跟随算法,图6采用另一种可行算法双边跟随算法. 图3 有障碍环境下8个移动机器人编队行进仿真Fig.3 Simulation of 8 mobile robots formation in obstacle environment 图4 无障碍物环境下50个移动机器人本文算法仿真Fig.4 This paper algorithm simulation of 50 mobile robots in obstacle free environment 图5 无障碍物环境下50个移动机器人单边跟随算法仿真Fig.5 Simulation of one side following algorithm for 50 mobile robots in obstacle free environment 图6 无障碍物环境下50个移动机器人双边跟随算法仿真Fig.6 Simulation of two side following algorithm for 50 mobile robots in obstacle free environment 图3(a)–(e)展示了有障碍环境下8移动机器人整个编队行进过程,图3(f)为整个过程的轨迹图,能够更加清晰地看到每个机器人个体的移动轨迹.图中每个小五角星代表一个移动机器人,圆代表障碍物,且障碍物周围有代表避障的圆环,圆环以障碍物为圆心,do为半径,若是移动机器人进入环便会进行避障. 接下来是图3中各图展示的具体内容. 图3(a)中的移动机器人的位置是随机初始化的. 图3(b)在20步时原本杂乱无章的移动机器人在编队行进算法的控制下已经能够初步形成线形编队,并且编队的角度和距离以及形状在不断趋近于设定值. 图3(c)–(d)中展示的都是避障过程,可以看到移动机器人在进入圆环的范围内后便开始主动分裂队形,以此避开最前面的障碍物,在避开最前面的障碍物后便不受到最前面障碍物的作用,但是由于偏后的两个障碍物作用,机器人队形再次分裂,最终成功避开了所有障碍物. 图3(e)展示了机器人编队在避开障碍物后再次切换至编队行进行为,根据此时周围环境信息来建立相互联系,并且最终重新形成设定队形. 图3(f)展示了整个过程机器人编队的轨迹,一开始从随机分布的状态集合成线形,接着遇到障碍物便开始避障,最后离开障碍物范围,重新组织队形.可以看到,整个过程中未发生碰撞,并且整个系统在遇到障碍物后可以看作系统受到外界扰动,扰动破坏了系统的稳定性但是在扰动结束后系统便再次趋于稳定. 图4–6中的(a)–(d)分别展示了相同时刻无障碍环境下50个移动机器人编队行进过程,以方便对比,并且设定. 图4–6的图(a)中可以看出3种算法都应用在相同初始位置的群机器人上. 3种算法的图(b)可以看出本文算法与双边跟随算法形成的形状基本相同,这是由于本文算法设计使得机器人群体在大幅调整时采取双边跟随策略,此时对比单边跟随算法发现若采用最小二乘法拟合单边跟随算法,其方差相较于本文算法和双边跟随算法更大. 图(c)中50步到100步的过程中本文算法通过位置预测行为采取单边跟随算法,此时双边跟随仍然在其50步的基础上调整,但是调整较慢,而单边跟随算法由于一直处在大幅调整状态下此时方差仍然很大,而本文算法的队形已经基本形成. 图(d)中在220步时,本文算法与单边跟随算法已经形成设定的编队,而双边跟随算法还未完全收敛到直线. 从上述3个仿真实验可以看出3种算法的优劣,首先是单边跟随算法,由于其只参考一个方向上的关联机器人,其在最开始的时候方差收敛的最慢,并且由于其跟随的机器人也处于调整状态,其能量消耗也会最大,其优势在于能够快速形成给定编队.双边跟随算法的优势在于其能够充分利用所有关联机器人信息,最开始的时候收敛地快,但由于该方法未考虑给定队形设置导致该方法形成给定编队需要的时间非常长,需要长时间的调整. 两种方法优缺点产生原因如下:由于假设机器人无法获得全局信息和所有机器人的位置信息,只能获得临近机器人的信息和给定队形信息,由于无法获取自身处于队形中的什么位置,单边跟随算法只参考一个方向相邻机器人位置和给定队形信息导致算法调整会出现朝着形成队形相反的方向调整的情况,而双边跟随算法虽然未知全局信息,但是通过两个方向相邻机器人位置可以缓解朝着形成队形相反的方向调整的情况,但是无法同时考虑队形信息导致其调整到给定队形的时间过长. 本文算法通过加入位置预测行为结合单边跟随和双边跟随算法的优点,在最开始的的时候能够采取双边跟随的策略快速收敛,并且计算此时的速度作为位置预测的在其收敛速度下降,机器人趋于稳定之后通过预测其在队形中的位置,朝形成队形的参考机器人方向移动,最终也能够快速形成给定编队,并且消耗能量大大小于单边跟随算法. 为比较算法性能,从形成直线的时间和能量消耗方面来进行对比分析.下面将一种群体期望队形方向llw和群体期望速度vlw不同仿真机器人数量(分别为50个、100个、150个、200个)作为一组仿真实验. 5.3.1 单组仿真结果 图7–8为用最小二乘法对机器人形成曲线拟合的结果,图9为随着迭代次数的增加总能量消耗曲线.子图(a)–(d)分别代表50,100,150,200个机器人进行仿真的情况,图中横轴为迭代次数,在机器人个数较少为50或100时设定最大迭代次数为500,而当个数为150或200时设定最大迭代次数为1000.图7为其拟合得到的斜率的弧度值,图8为每个点距离拟合得到直线的方差.此处同样设定和vlw=(5 0)T.图9表示从0时刻开始所有机器人速度求平均之后平方的累加,即,其中图7中的曲线越快收敛到1.04720,图8中的曲线越快收敛到0表示算法形成设定编队的速度越快,而图9中曲线越小表示算法消耗能量越小. 图7 最小二乘法拟合机器人编队的斜率(rad)变化曲线Fig.7 The least square method is used to fit the slope(rad)curve of robot formation 图8 最小二乘法拟合机器人编队的方差变化曲线Fig.8 Fitting variance curve of robot formation with least square method 图9 能量消耗曲线Fig.9 Energy consumption curve 结合图7–8分析发现:双边跟随算法斜率调整比较平滑,但其最终到收敛需要的时间非常长,甚至在达到最大迭代次数依然未收敛,而对比单边跟随算法斜率调整波动较大,但其最终能够收敛到设定值,而本文算法结合了两者的优点,在开始的时候与双边跟随算法相同平滑收敛,而后采取位置预测行为,快速收敛到设定值,波动也比单边跟随算法小,这是由于机器人群体首先收敛到了比较近的位置,并且根据预测位置有选择地跟随对形成设定编队有利的关联机器人,这样本文算法能够结合单边跟随和双边跟随两种算法的优点,在收敛时间方面本文算法大大优于收敛缓慢的双边跟随算法. 分析图9的能量消耗可以看出,由于本文算法是在采取双边跟随算法后进行预测,其能量消耗相较于双边跟随算法有所增加,但增加的较少,而单边跟随算法由于需要经过大幅调整过程,其能量消耗多于双边跟随算法和本文算法.因此,在能量消耗方面本文算法大大优于单边跟随算法. 5.3.2 多组仿真结果 为保证算法的鲁棒性,又分别对多组设定值进行了仿真,得到的结果曲线与图7–9类似.得到的结果统计如图10–12所示. 图10 斜率收敛误差棒Fig.10 Slope convergence error bar 图10–12中以误差棒的形式综合统计结果,误差棒中间的点表示多组数据的平均值,误差棒最上方的短线表示多组数据中的最大值,误差棒最下方的短线表示多组数据的最小值,图中横轴都为机器人个数(50个、100个、150 个、200个).图10的纵轴为斜率收敛至与设定值相差1◦以内的迭代步长,图11的纵轴为方差收敛到0.005以内时的迭代步长,图12的纵轴为最大迭代步长时机器人群的能量消耗.由于双边跟随算法直到最大迭代步长都未收敛,图10–11中未画出其收敛步长,其步长远大于最大迭代步长. 图11 方差收敛误差棒Fig.11 Variance convergence error bar 通过图10与图11分析对比本文算法与单边跟随算法,本文算法的收敛时间小于单边跟随算法和双边跟随算法,图12可以明显看出本文算法能量明显小于单边跟随算法.本文算法在收敛时间和能量消耗上均优于单边跟随算法. 图12 能量消耗误差棒Fig.12 Energy consumption error bar 本文提出了一种对通讯依赖不强的分布式多机器人线形编队控制算法,该算法能够在无法获取全局信息的前提下,设计了通讯受限条件下的机器人编队以及避障算法,使得机器人个体能够从初始随机位置出发形成设定编队,在编队行进的过程中避开障碍物,且在脱离障碍物范围后能够恢复线形编队.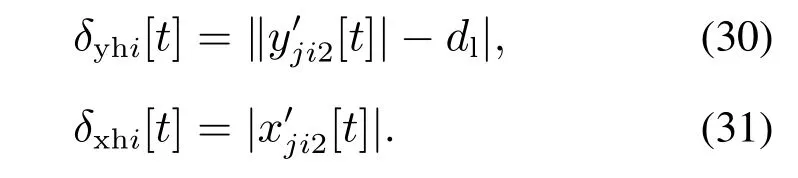

5 仿真实验


5.1 有障碍条件下的仿真与分析
5.2 无障碍条件下的仿真与分析
5.3 队形评估和能量消耗分析
6 结论

