带有完全分布式观测器的多智能体系统自适应容错一致性

尹艳辉 王付永 刘忠信陈增强

(1.南开大学人工智能学院,天津 300350;2.南开大学智能机器人技术重点实验室,天津 300350)

1 引言

近年来,多智能体协同控制成为国内外的研究热点,并广泛应用于卫星编队[1]、无人机[2]、传感器网络[3]等领域.一致性问题作为多智能体系统的基本问题,其研究的基本内容是基于局部信息设计分布式控制器,使整个系统的状态收敛到相同的值.到目前为止,多智能体一致性相关研究取得了丰富的成果[4–7].在一致性研究基础上,编队控制[8–9]、包容控制[10–11]等相关问题也被众多学者广泛研究.

由于物理特性限制、执行器件老化等因素的影响,执行器故障普遍存在实际系统中.对于多智能体系统来说,发生在单个智能体上的故障,可通过信息交换,影响邻居个体,甚至造成整个系统失稳.因此,对多智能体容错控制的研究具有重要的理论与实际意义.很多学者致力于设计和分析多智能体容错控制方案[12–20].文献[12]利用最优控制理论研究了一类多智能体系统的容错控制问题.文中证明部分失效故障不会影响系统一致性的实现.而当某些智能体发生完全失效故障时,一致性将不能得到保证.领导者将会调整自己的状态与发生故障的跟随者一致.文献[15]研究了针对线性和李普希茨非线性系统的容错控制问题.针对部分失效故障设计了自适应容错控制器.然而,文献[15]并未考虑完全失效故障与偏置故障的影响,并且文中控制器的参数配置依赖于求解多个复杂的线性矩阵不等式.文献[17]研究了一类模型参数未知且带有偏置故障的多智能体容错控制问题.通过引入一种带有边权重的动力学方程,并结合自适应动态规划技术提出了适用于无向固定拓扑的数据驱动一致性算法.文献[18]针对带有欺骗攻击和偏置故障的多智能体系统设计了分布式脉冲控制算法,其中假设网络层和物理层的拓扑均是无向连通的.在有向切换拓扑下,文献[20]设计了一种分布式自适应容错控制方案,文中的控制器可以同时补偿多种故障的影响.然而,文中的观测器并不是完全分布式的,需要利用拉普拉斯矩阵的特征值.切换拓扑下该值较难基于局部信息获取,因此此观测器具有一定局限性.

另一方面,受建模误差、环境噪声等影响,智能体的模型通常包含未知非线性动态和非匹配干扰.虽然针对这两种不确定因素已有丰富的成果[21–24],但综合考虑复合执行器故障、非线性动态、非匹配干扰的研究尚未见到.这些因素大多是未知的、时变的,并具有不同的特性.上述文献中的方法较难保证系统的稳定性,需要设计多种补偿器协同作用的控制策略.

基于以上讨论,本文研究上述诸多不确定因素并存的多智能体容错控制问题.主要的创新性在于以下几点:1)与现有的文献相比,本文同时考虑多种执行器故障(包括执行器部分失效故障、完全失效故障、偏置故障、卡死故障),非匹配干扰,和异质的未知非线性动态并存的情况.这些因素在实际系统中是普遍存在的.因此本文考虑的模型更具一般性.2)本文设计了一种适用于有向切换拓扑的自适应观测器.此观测器是完全分布式的,即无需利用网络拓扑的特征值信息.利用平均驻留时间方法给出了观测误差收敛的充分条件.此外,此设计利用邻居的观测信息代替真实信息,可以抑制故障的信息通过拓扑传播.3)本文的容错控制方案既不依赖于复杂的高阶的线性矩阵不等式的可解性,又无需任何故障的上界或下界信息.这种设计方法可以有效降低控制器参数配置的难度.

2 预备知识和问题描述

2.1 图论

其中:L1σ(t)∈RN×1,L2σ(t)∈RN×N.

本文假设智能体的通信拓扑在有限的M个拓扑间切换,并将这些拓扑标记为1,2,···,M.定义集合M={1,2,···,M},则切换信号可以用分段常数函数σ(t):[0,+∞)→M表示.设初始时刻为t0,第k次切换时刻为tk,则对于任意的k≥0,σ(t)满足

设Nσ(tm,tn)表示σ(t)在区间[tm,tn)内的切换次数.对于任意的时间间隔[tm,tn)(n>m),如果存在非负常数N0和τa满足

则τa称为区间[tm,tn)的平均驻留时间.

2.2 问题描述

多智能体动力学模型描述为

其中ρij为满足0 ≤ρij≤1的未知系数,表示第j个执行器的失效程度.ψij(t)表示未知偏置故障且满足‖ψij(t)‖<+∞.当ρij=1,ψij(t)=0时,第j个执行器无故障;当0<ρij <1时,第j个执行器发生部分失效故障;当ρij=0时,执行器发生完全失效故障;当某时刻ψij(t)≠0时,则该时刻第j个执行器发生偏置故障.特别的,如果ρij=0,ψij(t)为非零常数,则称此种状态下的执行器故障为卡死故障.为方便分析,将式(3)写为,其中

定义全局误差

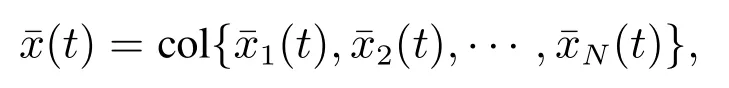
假设1对于任意的p ∈M,Gp存在以领导者为根节点的有向生成树.

假设2对任意的i ∈V {0},有

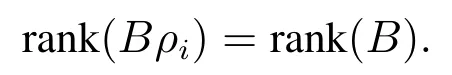
假设3直到m −1个执行器发生完全失效故障,剩余的执行器仍能实现控制目标.

注1假设1保证跟随者能够间接获得领导者的信息.假设2表示执行器存在冗余[25].假设3保证了容错问题的可解性.

引理1[26]若假设1成立,对任意的p ∈M,存在正定的对角阵Πp=diag{π1p,···,πNp}满足

其中Υp是对称正定矩阵.

引理2[27]若线性系统

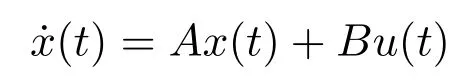
满足A是赫尔维茨矩阵,,则该系统原点是渐近稳定的.

3 基于分布式观测器的容错一致性控制器

3.1 分布式自适应观测器

有向切换拓扑下信息具有不对称性,直接设计容错控制器会导致不同智能体间的自适应模块互相干扰.因此,将采用观测器来估计领导者的状态.假设σ(tk)=p ∈M,t ∈[tk,tk+1).自适应观测器为

注2定理1的创新性在于,设计了一种适用于有向切换拓扑的分布式观测器.与文献[20]中的观测器相比,定理1的方案是完全分布式的,即无需Υp的最小特征值信息.该信息属于全局信息,对于单个的智能体来说无法通过有限的通信能力获取.并且在切换拓扑下,该信息是时变的,会给控制器设计带来更多困难.定理1结合了自适应方法和平均驻留时间概念,给出了观测误差最终一致有界的一个充分条件.

3.2 基于神经网络的容错控制器设计

设e=col{e1,e2,···,eN},其中ei=xi −ξi表示智能体状态和观测信号的跟踪误差.由式(2)(4)可得

注3受引理2启发,本文并未根据传统反步法的思想直接设计虚拟控制器使子系统(16)稳定.而是从系统可控性出发,使子系统(16)满足引理2中条件.根据经典文献[28]中的结论,P¯的存在意味着是赫尔维茨的.这种处理的好处是,控制器的设计只需原系统可控作为前提条件,而并不依赖于复杂线性矩阵不等式的可解性.

本文设计的容错控制器具有如下结构:

其中:uin是误差反馈控制,uig1,uig2和uif分别是具有不同作用的故障补偿器.基于自适应控制的思想,uin设计如下:

注4本文设计的3个故障补偿器分别具有不同的特点:uig1用于补偿已知的与状态相关的动态的影响;uig2用于补偿未知的独立于状态的干扰的影响;uif用于补偿未知的与状态相关的动态的影响.值得注意的是,虽然gi1是已知的动态,但是由于部分失效故障的存在,仍旧需要设计独立的自适应模块.在3种补偿器的共同作用下,本文设计的容错控制器具有较强的鲁棒性.

注5由于fi(xi)是未知的、异质的,且不满足李普希茨条件,本文利用神经网络强大的逼近能力来设计补偿器.补偿器中采用的估计来代替传统RBFNN中对的分量的估计,可以避免控制器设计的过度参数化.

注6综合定理1和定理2可以看出,本文的容错控制器设计仅仅依赖于原系统的可控性,即控制器参数仅与系统参数A与B相关.作为对比,文献[29]需要求解包含拉普拉斯阵的特征值的线性矩阵不等式,文献[30]需要求解包含故障信息的线性矩阵不等式.当网络拓扑发生变化或故障加重时,这些条件可能被破坏导致失稳.因此,本文的控制方案具有更好的鲁棒性.此外,本文未采用传统的自适应投影算法设计控制器.该算法需要已知乘性故障的ρi上界和下界.事实上,本文的控制器设计无需任何故障因子的边界信息.这种设计可以使容错控制方案具有更好的自适应性.

4 数值仿真

本节考虑由一个领导者和3个跟随者组成的系统,其拓扑如图1所示.

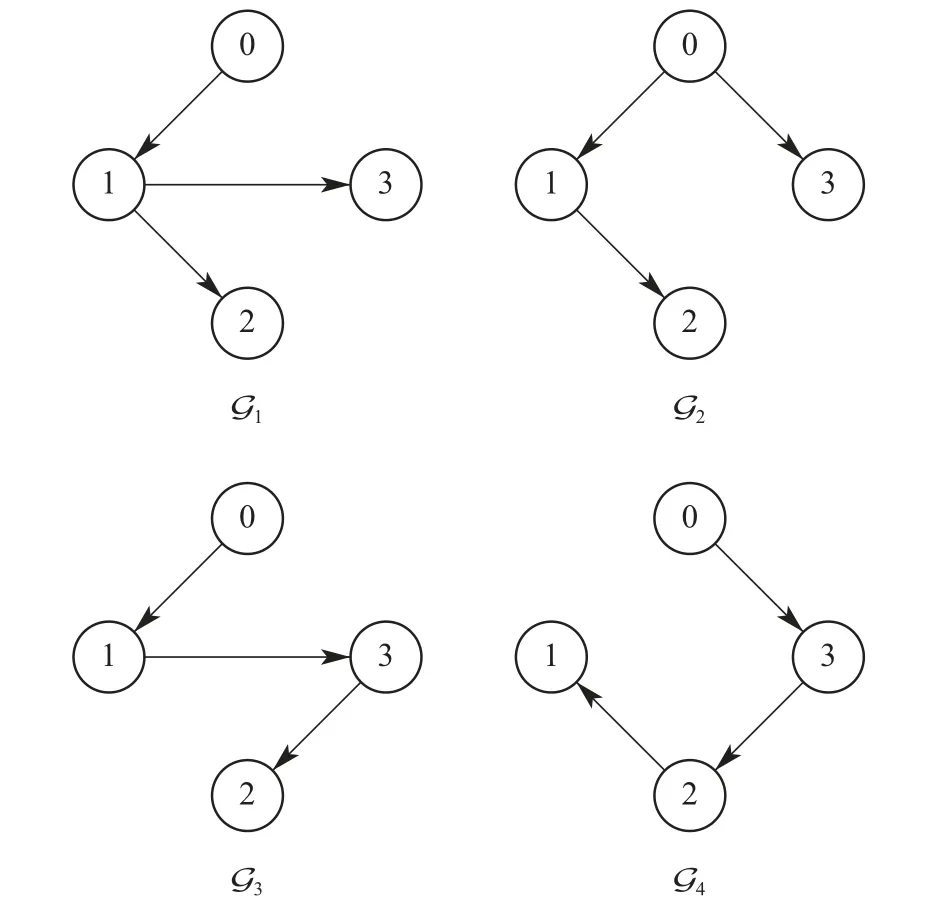
图1 智能体间通信拓扑Fig.1 Communication topologies of the considered MAS

假设系统相关参数为

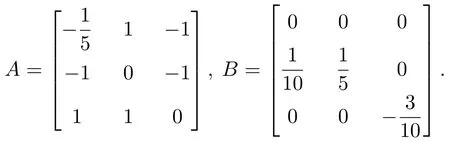
非线性动态为

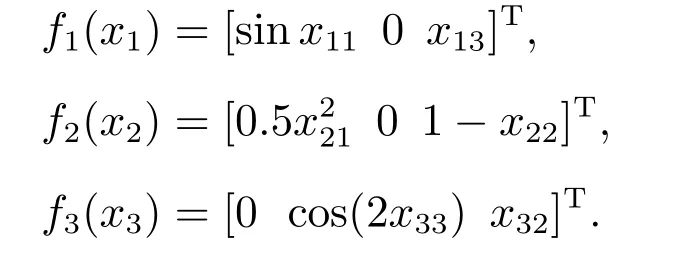
非匹配干扰为w1=w2=e−t1,w3=2−t1.假设跟随者1和2 带有执行器故障,具体描述为

根据定理1和定理2可计算相关黎卡提方程一组解为

本小节使用的RBFNN包含64个神经元,其中心平均分布于[−2,2]×[−2,2]×[−2,2]中.基函数宽度均设为2.设xi(t0)在[−10,10]×[−10,10]×[−10,10]中随机选取.自适应参数初值均设为0,步长γij=0.1,i=1,2,3,j=1,2,3,4.在如图2描绘的切换信号下,智能体状态响应曲线如图3所示.从图中可以看出,本文所提的方案可在多种故障和未知动态的作用下实现容错一致性.作为对比,图4给出了文献[20]中的控制方案下的状态曲线,其中c0=1,=0,ε1,i=ε2,i=0.1.综合图3和图4可以看出,在上述故障与初值条件下,本文所提算法具有更好的控制效果.图5–7分别描绘了控制器中5种自适应参数的变化曲线,图8为控制信号的变化曲线.显然闭环系统的所有信号都是有界的.

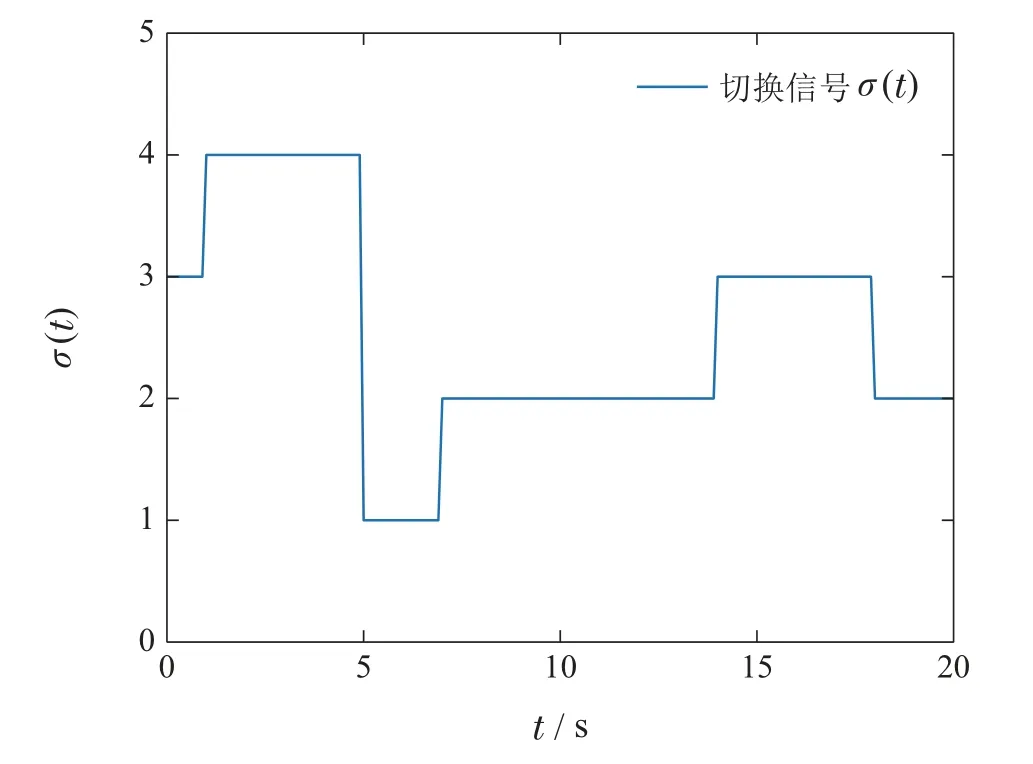
图2 切换信号σ(t)变化曲线Fig.2 Response curves of σ(t)

图3 智能体状态变化曲线Fig.3 Response curves of xi

图4 文献[20]控制方案下智能体状态变化曲线Fig.4 Response curves of xi under the protocol in[20]

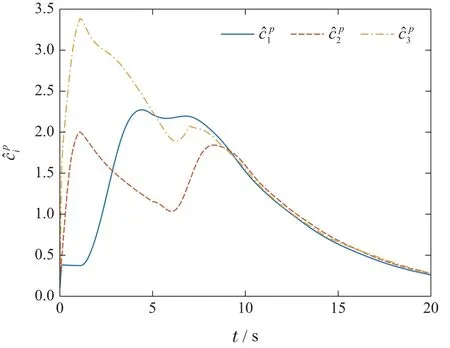
图5 自适应参数 变化曲线Fig.5 Response curves of

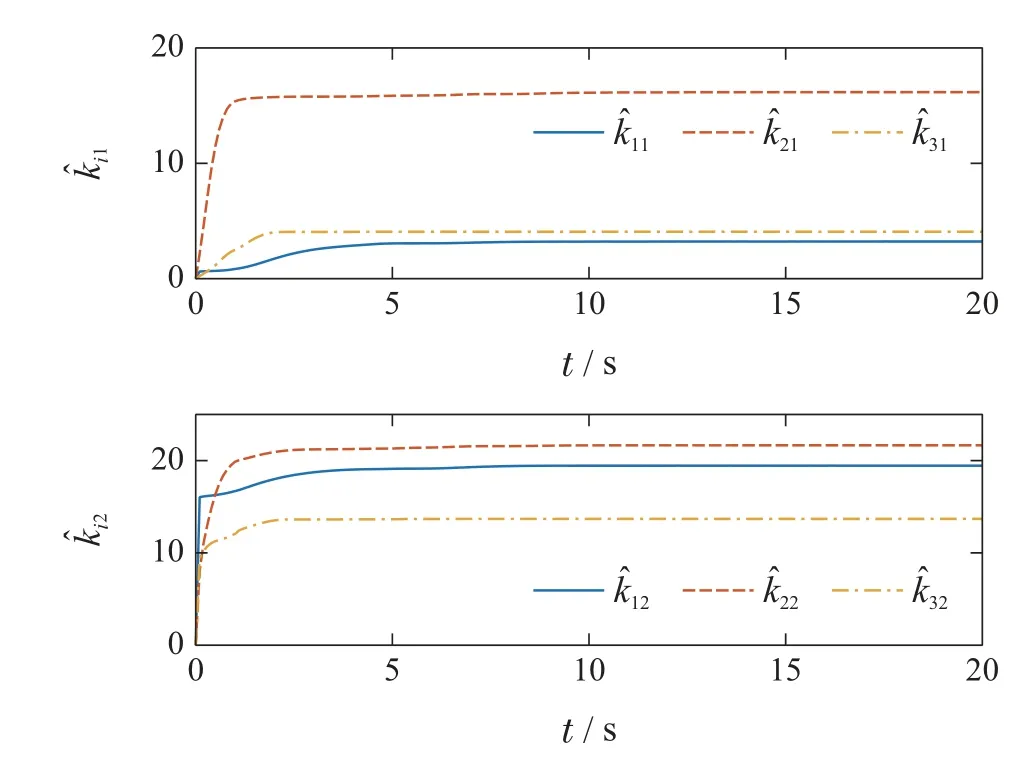
图6 自适应参数,变化曲线Fig.6 Response curves of and

图7 自适应参数,变化曲线Fig.7 Response curves of and

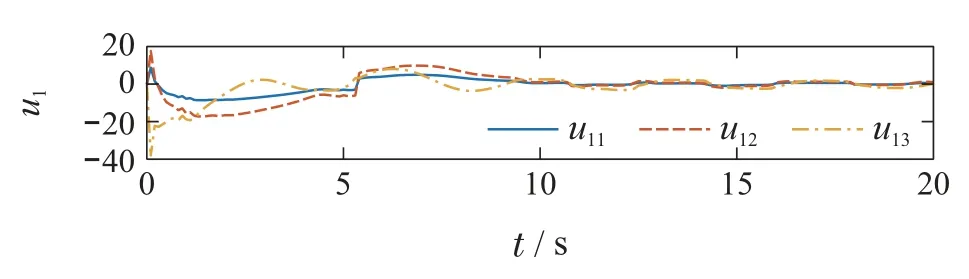
图8 智能体控制信号变化曲线Fig.8 Response curves of ui

5 结论

本文提出了一种新的适用于有向切换拓扑的多智能体容错控制方案.综合利用了自适应控制、反步法、径向基神经网络等技术设计观测器和容错控制器.基于平均驻留时间和Lyapunov稳定理论给出了一致性误差最终一致有界的充分条件.本文提出的方案是完全分布式的,且参数配置不依赖于求解复杂的线性矩阵不等式.数值仿真证明本文的控制方案对多种不确定性及故障有良好的鲁棒性.

本文假定网络通信环境是较为理想的,而实际系统中,智能体间的通信可能存在干扰、时延、丢包,甚至网络攻击.因此笔者未来将致力于解决复杂通信环境下的多智能体容错一致性问题.