基于改进的跟随领航者与人工势场的CGF队形控制及避障∗
(海军航空大学 烟台 264001)
1 引言
计算机兵力生成(Computer Generated Forces)技术可在虚拟战场中产生具有一定自治性、智能性的仿真实体,并由程序语言来控制其运动[1]。随着科学技术的不断进步,战场环境复杂度不断增加,对作战人员的能力要求越来越高。单个兵力的感知、决策、学习能力都很有限,若能使单个兵力具备一定的协作能力,在团队中保持队形行进,与其他CGF实体进行更好的通信协作,更有助于完成复杂任务[2]。因此研究CGF实体团队如何在行进中保持队形,并能够对障碍物进行主动避障愈加必要。
现今对机动团体队形保持的算法有很多,如跟随领航者法(Leader-Follower)、基于行为法和虚拟结构法等[3~5]。跟随领航者(Leader-Follower)法是选出CGF编队中的一个Agent实体并将其作为机动团体的领航者(Leader),其余Agent实体作为跟随者(Follower)跟随领航者运动,在行进时通过使跟随者与领航者之间的距离值、方向角度误差保持在期望水平,使CGF编队保持一定的战术队形行进,完成对队形的控制[6~9]。基于行为法是将每一个Agent实体的机动行为分解为向目标运动、保持队形、避障等部分,对自身的机动行为实施控制。人工势场法是将物理学中的势场等原理运用到队形控制算法中[10~11],对目标点、障碍物、队伍中的其他Agent实体进行势场的人为定义,使每一个Agent实体都在一个综合人工势场中运动,不断向势能最弱的点运动最终到达目标点,并实现运动中的避障功能[12~14]。
经分析,跟随领航者法的优点在于其控制器的设计相对简单,并在实施过程中只需要使跟随者对领航者的运动轨迹进行跟踪并获得其运动状态信息,同时简化了各Agent实体间的通信协作问题[15]。因此采用跟随领航者算法对队形实施控制。但该方法的缺点是整个机动过程太过于依赖领航者,并且领航者与其跟随者之间没有明确的运动误差反馈。若在避开障碍物时领航者因为运动轨迹的变化而突然提速,其余跟随者可能因为无法跟上领航者从而丢失跟踪目标,最终导致队形形成的失败;并且领航者作为该算法中的核心,如果领航者发生故障等难以预期的突发状况,将会导致整个CGF编队失去原有运动阵型,作战任务失败的后果[16]。为解决这一问题,本文引入虚拟领航者的方法,并设定虚拟领航者只负责向目标前进,不受障碍物的限制,并结合基于行为法的思想,将整个机动过程分解为虚拟领航者向目标运动、跟随者队形控制、避障等部分,降低了跟随者对领航者的依赖性,提高了算法的容错率,最后运用人工势场法进行对障碍物的躲避。经仿真分析,此方法有效地使CGF编队在行进过程中保持良好队形,能够及时避障,并迅速回到规定队形继续运动,满足了系统的实际需求,具有良好的适应性与可操作性[17]。
2 队形控制及避障
2.1 跟踪控制算法分析
在行进过程中使Agent实体保持队形的关键就是让跟随者始终紧跟领航者的步伐,即具备一定的跟踪能力,这是跟随领航者算法实现编队队形控制的基础与核心[18]。
为能更清晰地描述各Agent之间的关系,本文将CGF队形以矩阵形式表示,位置关系表达式为

以三角阵型为例,如图1所示。则队形的数据结构表示为
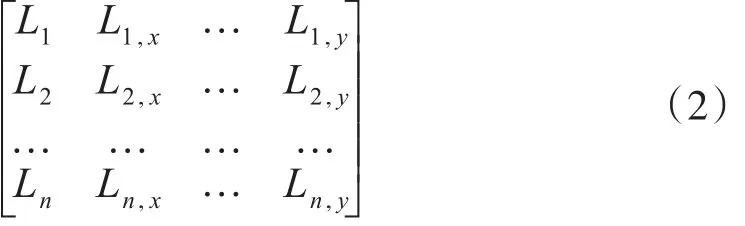
建立Agent的动力学模型:

其中,Agent当前位置表示为 Z=(x,y)T,当前速度 表 示 为 V=(V,V)T,控 制 输 入 量 为
xyU=(u1,u2)T ,则Agent动力学模型可表示为 Z̈=U 。

图1 三角阵型下的Agent位置关系
2.1.2 虚拟领航者向目标前进

其中,θ为虚拟领航者与目标的偏角,V0为虚拟领航者的运动速度,其大小和方向恒定。
2.1.3 跟随者队形保持算法
2.2 2组治疗前后RDQ量表评分比较 2组治疗后反酸、反流、烧心及胸痛等RDQ量表评分比较。中年治疗组与对照组比较,χ2=4.24,P=0.039(P<0.05),差异具有统计学意义;老年治疗组与对照组比较,χ2=10.881,P=0.001(P<0.05),差异具有统计学意义;中老年治疗组比较,χ2=4.9,P=0.028(P<0.05),差异具有统计学意义;中老年对照组比较,χ2=0.60,P=0.438(P>0.05),差异无统计学意义。详见表2。
在图1中,Agent i与领航者的期望位置差为

2.2 队形避障算法分析
为避免因领航者发生故障而使整个团体无法继续运动的情况发生[19~20],设定虚拟领航者始终只受目标点的吸引力,与其他Agent实体无相互作用力,同时可以穿过障碍物,以此保证其在行进过程中不会发生故障。
图2为引入虚拟领航者后三角阵型下的各Agent受力图。 fl为跟随者受到的来自虚拟领航者的控制作用力,其大小与距虚拟领航者的距离有关;ff为其他跟随者对其产生的斥力,避免团队在行进过程中内部发生碰撞,其大小与距其他Agent的距离有关;fr为障碍物对跟随者产生的斥力,其大小与距障碍物的距离有关;当跟随者的速度与期望速度不符时(期望速度为跟随者在虚拟领航者的带领下运动的值),会受到一个控制作用力 fv,而当速度达到了期望速度时,fv为零。
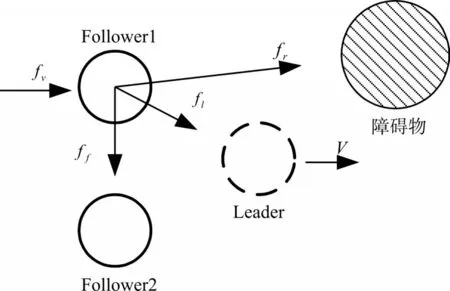
图2 Agent受力图
引力场函数:
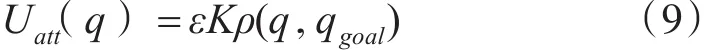
其中,ε是引力比例因子,ε>0,K是目标点引力强度,ρ(q , qgoal)是领航者与目标之间的距离。相应的引力函数为

而障碍物和团队中的其他伙伴对Agent产生斥力,斥力函数为
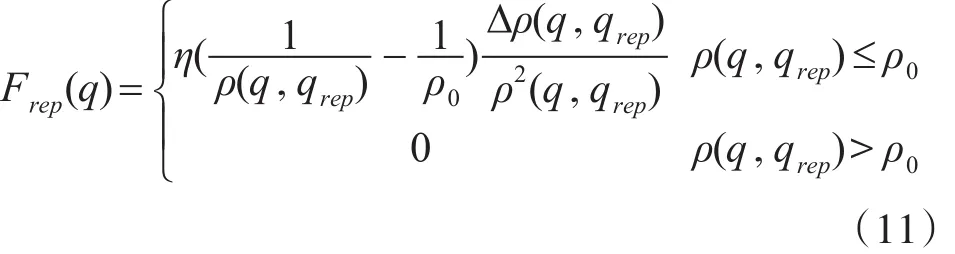
其中,η是斥力比例因子,η>0,ρ(q , qrep)是Agent与障碍物或其他Agent的距离,ρ0是安全距离,若超出此距离,则障碍物或其他Agent对Agent的运动轨迹不产生影响,即没有斥力作用。因此,Agent所受合力为
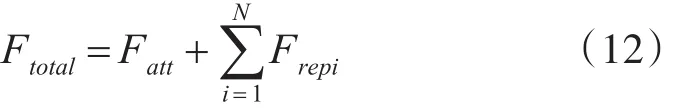
Agent运动方向为所受合力方向,运动速度与所受合力成正比:

其中,λ为合力速度比例因子。
3 仿真实验及结果分析
3.1 CGF跟踪控制
将虚拟领航者的初始速度设为40,期望角度差 为 2π/3 ,l1,x=100 ,l1,y=200 ,ΔZi,d=40 ,ki=7,df=1。图3为跟随者1的速度变化图,图4为跟踪过程中跟随者与领航者的运动角度差,可知跟随者为跟上领航者先大幅度提速转向领航者运动,在与其距离达到期望距离后逐渐减速,运动方向转向目标点,速度向领航者不断趋近,最终与领航者保持速度与步调一致。图5为领航者与跟随者1的轨迹变化图,可知实现了Agent间的跟踪控制,保证了队形的形成及控制。
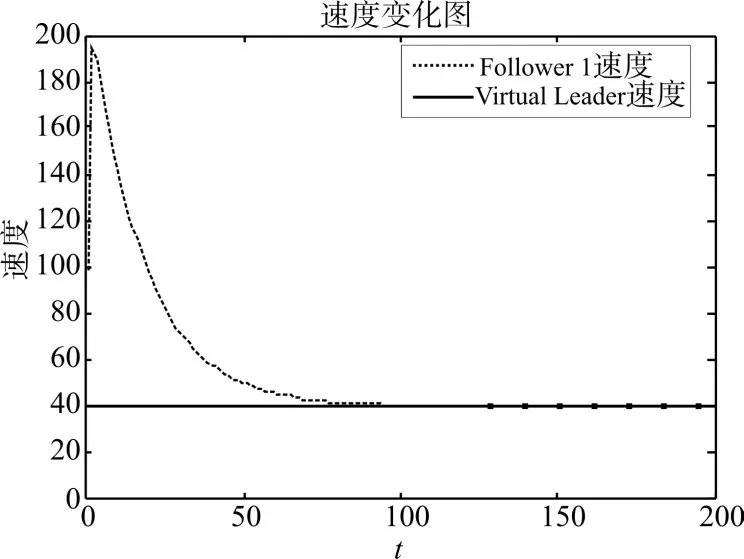
图3 跟随者速度变化
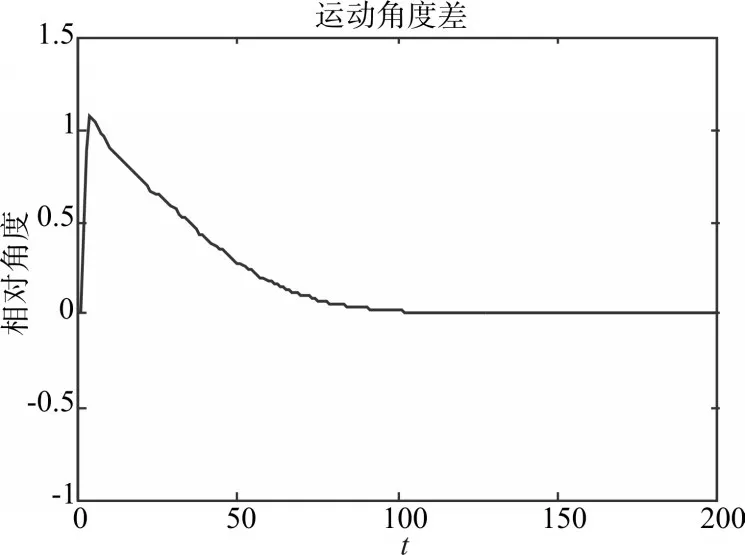
图4 运动角度差变化
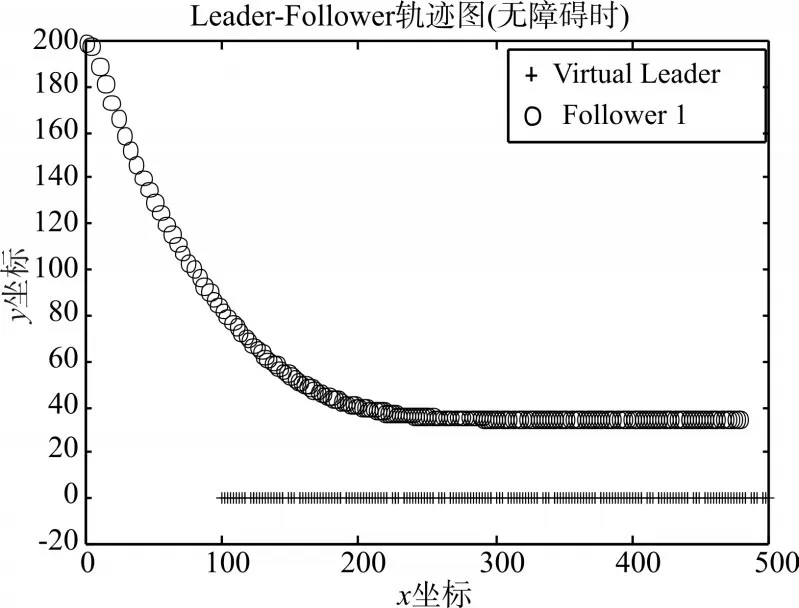
图5 无障碍时Leader-Follower轨迹图
3.2 CGF避障仿真结果
以三角队形为例,在500×500的坐标范围内随机生成四个点,以其为圆心建立障碍物,其半径在[20,150]区 间 随 机 取 值 ,设 l1,x=l2,x=100 ,l1,y=200 ,l2,y=-200 ,由仿真结果可知,Agent能够及时躲避障碍物,并迅速回到规定队形,保证了队形的可控性与安全性。
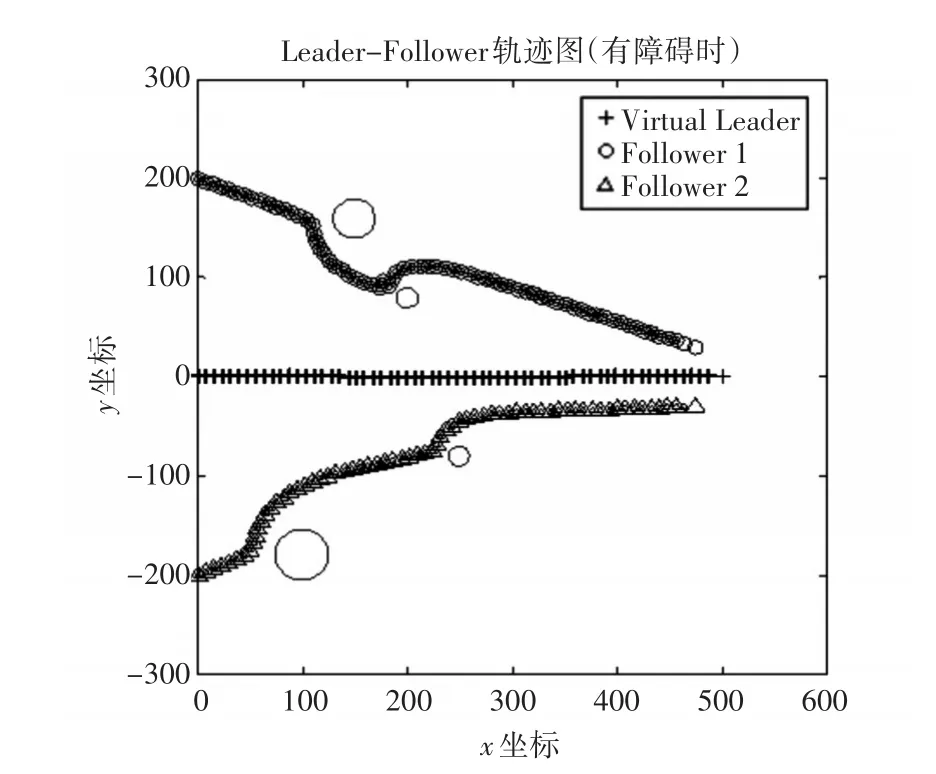
图6 Leader-Follower轨迹图(有障碍时)
4 结语
本文通过运用已有的跟随领航者算法,结合基于行为法的思想加以优化,再引入虚拟领航者的思想,最后采用人工势场法进行对障碍物的躲避,仿真结果表明该方法能有效使CGF编队避开障碍物,以期望队形到达目标点。本文中只研究了一个CGF编队只有一个虚拟领航者的情况,在处理复杂作战任务时设置多个领航者的情况可作为下一步的研究方向。
—— 瓮福集团PPA项目成为搅动市场的“鲶鱼”

