用儿童的方式抵达数学的内核
——《角的度量》教学实践与思考
文 曹炯 沈杰
角的度量是继长度之后几何度量的第二个教学阶段,是发展学生空间观念的重要学习内容与载体。长度与角度虽然都隶属于图形的测量领域,但两者在测量方式、思维结构上存在较大差异。基于学生空间观念发展与度量能力提升的思考,笔者遵循学生认知发展规律,从课堂前测反馈和角的概念入手,以描角方式降低测量起始难度,最后横向打通角与量角器的数学结构,对角的测量教学做出有益的探索与尝试。
一、起点剖析——厘清学生量角的认知障碍
为了了解学生的学习状态与认知层级,课前笔者对四年级学生进行了量角的针对性课堂前测问卷调查,从学生反馈的结果中得出:角的度量已超越学生以往的空间几何认知结构储备。一是角的结构无法对应认知。二年级的长度测量对象是线段,从学生的视觉直观层面是一条“直直的线段,像一根拉长的毛线”,而角已经突破一维的线性认识,转入更为抽象的二维世界的结构表达,它已不属于“笔直的长度”范畴,而是一个崭新的“弯曲的弧度”的范畴,这是结构的根本转变。二是几何经验无力支撑测量。测量需要工具,学生的工具只有直尺,现在改变测量工具,学生一时无法了解量角器本身的数学结构和测量方法,难以找到像以往测量时的起点与终点。同时量角器的内外圈读数的复杂性也对学生测量造成一定的困扰。
二、借势而导——丰厚外显因素的空间知觉
直觉思维在小学空间与几何的学习中较为常用,学生对图形初步感知往往偏重于直观性较强的属性特征。角的两条边虽然降低了空间延伸的几何视角维度,但无形中却提升了生活视角量角的契合度和边界性。基于以上思考,笔者在课堂的起始部分以描角的方式将学生的直觉思维与抽象的角尝试无缝衔接。
【教学环节一】尝试描角,正确认读
1.在纸质量角器上描出40 度的角。
(教师呈现学生作品,并标上∠1、∠2)
师:怎么看出∠1 是40 度的?
生:4 个大格就是40 度。
生:角上的刻度是从0 到40。(教师用水笔描出0 到40 的弧线)
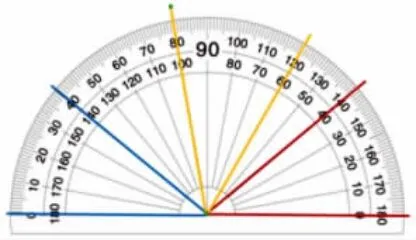
师:∠2 是40°又是怎么看的?
生:它也有4 个大格,所以是40°。
生:我是看外面的刻度的,也是从0 到40。
师:0 刻度线对着右面的时候,我们要看内圈,0 刻度线对着左面的时候,我们要看外圈。
师:你们还有其他描法吗?
(呈现学生作品)
师:中间那个是40 度吗?
生:是的,它有4 个大格。
生:100-60=40,从内圈的60到100 有4 个大格。
师:还有其他描法吗?
师:(呈现学生作品)还有个同学这样描的,你觉得他描得怎样?
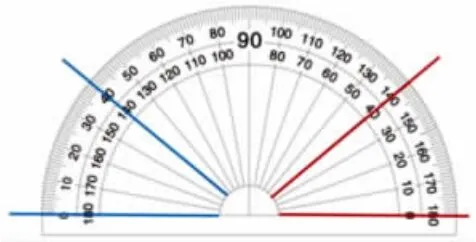
生:角的顶点没有了。
(学生上来补一补)
师:看来我们画一个角时,先要画顶点,再画两条边。现在看看这两个角是40°吗?
生:是的。
师:刚才在纸质量角器上面描出了40°的角,而且我们还学会了不同描法,只要角里面是4个大格,也就是4 个10°,都是40°。
【教学环节二】读出教师所描角的度数
师:(呈现大纸质量角器)老师画了几个角呢?这几个角分别是多少度呢?把你看到角的度数记录下来。
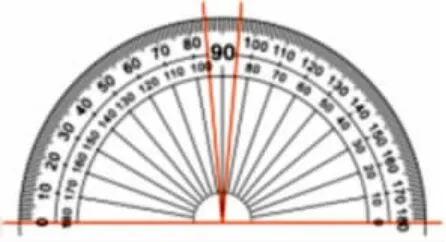
(学生记录各个角的度数。反馈:10°、85°、95°、180°)
师:我们来看最小的10°角,它在哪里?谁上来指一指?是怎么看出来的?
生:里面有10 个小格,每个小格是1°,10 个小格就是10°。
师:你们听明白了吗?10 个1°就是10°。
师:那85°又在哪里?你们都找到了吗?请你上来指一指。
师:那这个85°你们是怎么读出来的?
生:80°过去再数5 小格就是85°。(教师先描出0 到80,再描出80 到85)
师:那这个85°又是怎么看出来的?
生:从左边的0 刻度数过去,先到80,再过去5 小格就是85°。
师:谁也能像老师刚才这样描一描?(学生描出0 到85 的弧线)
师:95°角的一条边在这里,另一条边在哪里?谁来摆一摆?
(学生上来摆)
师:怎么读出来的?
生:90°再过5小格就是95°。
师:如果这条边往左移动1格,现在几度?96°,再移动1 格是几度?(教师动手移)
师:还有这个180°,它的两条边在哪里?
(学生摆出两条边,教师课件呈现180°)
【思考】
1.缓冲区:关注学生的认知起点,为理解而学。
因为受制于以往几何经验的影响,学生在前一课时中虽然对角有了初步的认识,但大多数学生还是以孤立、零散、碎片的形式理解,无法形成结构化知识。也就是说,量角的学习起点依然是角的结构认识,量角是角概念的思维派生。借助“描角”,让学生在纸质量角器中描出40 度角,并呈现不同40度角的思考方式,最后得出不管是看大格还是读刻度,其实质就是看这个角含有几个10°。这样不仅降低了量角对学生认知结构的正面冲击,同时构筑了角与量角器结构交集的“缓冲地带”,使学生更好地探索角的结构与量角器结构的数学对应原理。
2.发展区:优化工具的单一测量,为思维而教。
量角器以工具性的意义进入课堂势必会给学生造成思维负担和测量困扰,转变教学定向设计,使量角器的教学定义更为弹性化———学习材料。小学数学课程改革理念尤为重视在具体的感性材料里提取数学对象的本质特征,这是因为小学生正处于由具体形象思维向抽象思维的过渡阶段,需要直观材料和自身感性认识作强力支撑。将量角器作为学习材料,不仅能减少学生机械操作与生硬法则产生的负面测量情绪,更重要的是以测量角度为契机发展学生的空间结构,利用迁移知道一大格代表10°、一小格代表1°,帮助学生从纷繁复杂的表象中发现内在联系,积极创设思维发展的学习平台与环境,进一步构建与落实以促进学生数学发展的教学目标体系。
3.结构推进——追寻结构对应的数学法则
数学学习不是简单的习得某个显性的数学知识,在本质上是一个严谨、连贯的思维活动过程,也是学生智慧逐步生成、相关认识不断深化的过程。学生体验描角→识角之后,自然就会沿着达成量角的目标方向探索,教师虽然还没有正式讲授正确的量角方法,但对学生量角的理解已完成了实质化结构的转变。
【教学环节三】尝试量角与画角,掌握方法
1.量出练习纸上三个角的度数。
(1)学生独立量角,教师依次呈现学生的结果。
师:∠1 是55°,∠2 是120°,∠3 是38°。
师:再看第2 个同学的,∠1是55°,∠2 是60°,∠3 是39°。
师:再看看第3 个同学的,∠1是55°,∠2 是120°,∠3 是38°。
师:∠1 都是55°,我们就不讨论了。
(2)交流量角的方法。
师:∠2 有同学认为是120°,也有同学认为是60°,同学们有不同意见,如果不用量角器,你觉得哪个度数有可能是对的?
生:我觉得120°可能是对的,因为∠2 比直角大,它是一个钝角,所以度数肯定大于90°。
师:那∠2 是不是120°呢?请个同学上来量一量。(学生测量)
师:是120°吗?那这位同学量出60°,你们觉得他的问题在哪里?跟你的同桌讨论一下。
生:他估计是看外面的刻度60,没有看角的这条边对准的是哪条0 刻度线,所以内外圈搞错了。
师:如果这个角是60 度,那它的另一条边会在哪里?
生:在0 刻度线。
生:在120 刻度线。
师:这两条边都可以吗?
生:因为里面都有6 个大格。
师:∠3 也有不同结果,有人认为38°,有人认为39°,到底是几度?怎样才能读得更准一点呢?跟你的同桌商量一下。
生:把角的这条边沿长,那就能读得准了。
师:为什么可以把角的一条边延长?
生:延长时角的大小不变。
师:你们把边延长后再来测量一下∠3 的度数。
2.画出指定度数的角。
师:画一个30 度的角。
(1)学生独立画角。
(2)交流画角的方法。
师:刚才老师看到有几个同学觉得很难画,想不想看看?
师:他是先把量角器放在白纸上,然后在0°和30°的刻度点了两个点。然后把量角器拿走了,你们猜猜他们遇到了什么困难?
生:角的顶点找不到了。
师:谁愿意帮帮他们?
生:(学生上来画30 度角)我先画一条边,然后把量角器放在边上,中心点对准端点,然后在30°刻度处点一个点,最后把两个点连起来。
【思考】
1.测量本质的归纳。
描角与识角已为学生设置了探索量角的几何经验阶梯,但这两者并非是本节课的核心内容与学习终点。将学生的思考引向量角本质处,从之前习得的描角、识角作为后继量角学习的基础上导入自主量角。通过独立尝试、错误对比、方法辨析,学生对量角器的数学结构意义逐渐从模糊到清晰,得出“角的顶点和量角器的中心重合,一条边和0 刻度线重合,看另一条边所对应的刻度”的测量方法。更重要的是将其本质进行联通,即“都要看被度量的物体里含有多少个基本度量单位”。量角器材的二次使用是对学生数学思维的运用、组织和提炼,从而生成、凝聚新的测量法则,实现量角器与角的结构横向打通。
2.批判性思维的创生。
批判性思维是三大高阶思维之一,也是数学学习中连接意义理解和创造性建构的中间桥梁。量角器的内外圈测量方法势必会引发学生正确取值的混淆,这为学生批判性思维孕育了生长环境和契机。在测量∠2 度数到底是120°还是60°的讨论中,教师积极引导学生关注同伴,在阐述自己的理解与判断的同时,鼓励相互质疑与评价。学生在互相纠错中逐步获得学习主体的身份认同感,强化检验的元认知经验,独立思考的意识和理性思辨的能力不断完善,对权威依赖性日益减少,这是批判性思维品质形成的重要保障与实践路径。
对几何度量的教学需要贴近学生几何经验共鸣的学习材料,从表层的动手操作中建构深层的数学思维,为学生数学核心素养的发展寻觅一条高效、科学的教学路径。
——以“画角的复习”教学为例

