关于算术序列中素数的Dirichlet定理的某些注记

刘宝庆，钱 锟，李国全

（天津师范大学数学科学学院，天津300387）

1 引言及主要结论

以N表示全体非负整数的集合，记N+=N{0}.定义P={p∈N：p为素数}.对一个有限集A，以|A|表示其基数.设m、n∈N+，且n≥2，对于x≥1，定义

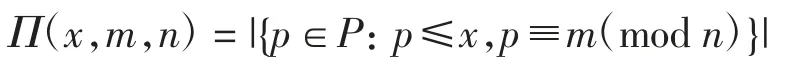
著名的Dirichlet定理[1]断言：如果（m，n）=1，则算术序列{m+jn：j∈N+}中含有无限多个素数，即m，n）=+∞.Dirichlet定理的一个精确形式为下面的定理1.

定理1[2]设m、n∈N+，且n≥2.如果（m，n）=1，则有

其中Φ（n）=|{l∈N+：l＜n，（l，n）=1}|.

对于一个集合B⊆P，定义其相对密度为

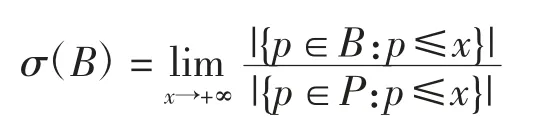
由熟知的素数定理，定理1蕴含下面的定理2.

定理2 设m、n∈N+，且n≥2.记B={p∈P：p≡m（modn）}.如果（m，n）=1，则

设Fq为一个含有q个元的有限域.以A=Fq[t]表示Fq上的多项式环，将它的商域Fq（t）记为K.对a、b∈A，且b≠0，定义：当a≠0时，当a=0时，|a|=0.则|·|为K上的一个非阿基米德绝对值.K在|·|下的完备化为

K∞是Fq上关于1/t的形式Laurent级数域.A、K和K∞分别起着与Z、Q和R类似的作用.关于A中的数论及K∞上的分析可参见文献[3-6].

A与Z有很多相似的数论性质，因此在框架A中考虑上面的问题是自然的.本文的目的是研究定理1和定理2在框架A中的对应结论.

设a、b∈A{0}，且degb≥1，对x≥1，定义

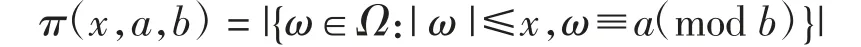
其中Ω={ω∈A：ω为首1不可约的}.关于定理1的对应结果，本文得到如下结论.

定理3 设a、b∈A{0}，且degb≥1，假设（a，b）=1.

（1）记ϕ（b）=|{c∈A：|c|＜|b|，（b，c）=1}|，则

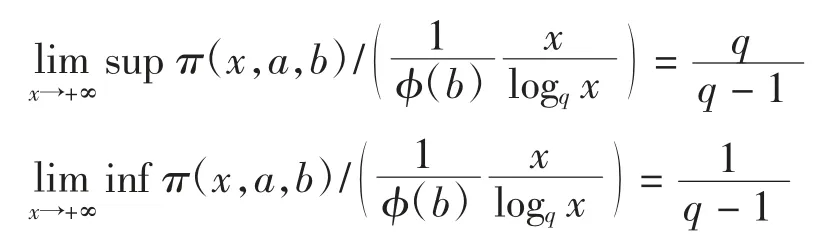
（2）对于1/q≤η≤1，存在数列{xN}，使得

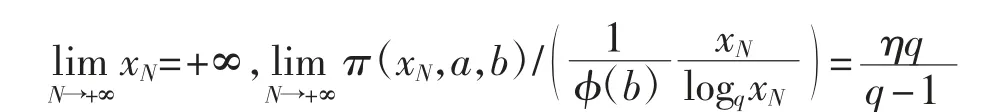
对于S⊆Ω，定义其相对密度为

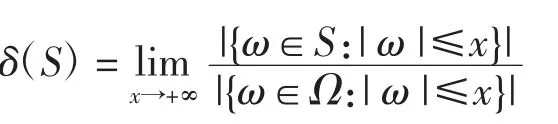
关于定理2的对应结果，本文得到如下结论.

定理4 设a、b∈A{0}，且degb≥1.记S={ω∈Ω：

设a∈A{0}，定义a的因子数为

D（a）=|{c∈A{0}：c为首1的，c|a}|

数论中的许多重要问题都涉及因子数估计，具体可参见文献[4-10].定理3和定理4的结果可用于估计A{0}中元的因子数.

定理5 存在一个仅与q有关的常数M≥1，使得对a∈A{0}，当|a|≥M时，有D（a）≤|a|1/lnln|a|.

推论[4]∀ε＞0，存在一个仅与q和ε有关的常数M′≥1，使得对于a∈A{0}，有D（a）≤M′|a|ε.

注上面推论是文献[4]给出的因子数估计.当|a|充分大时，定理5改进了文献[4]的结果.

2 主要结论的证明

设a、b∈A{0}，degb≥1，对N∈N+，设定义

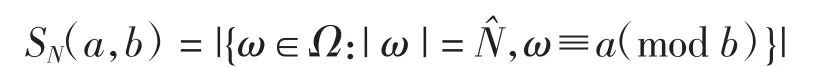
引理1[3]设a、b∈A{0}，且degb≥1.如果（a，b）=1，则其中C≥1是一个仅与q和degb有关的常数.

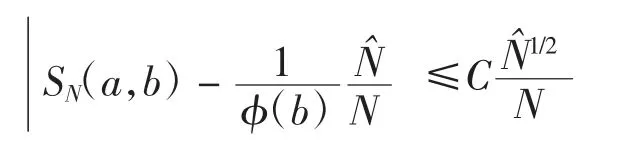
引理2 设a、b∈A{0}，且degb≥1.如果（a，b）=1，则数列{ϕ（b）Nπ（Nˆ，a，b）/Nˆ}是收敛的，具体地，有

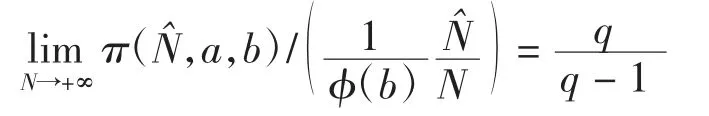
证明由引理1可得

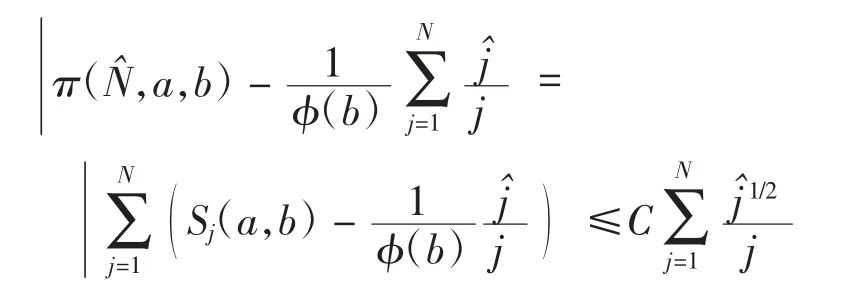
因为

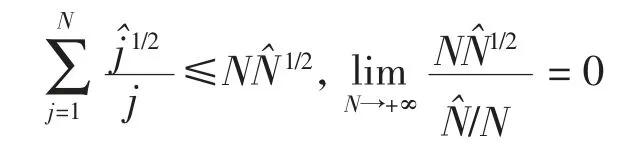
为证明引理，只需说明

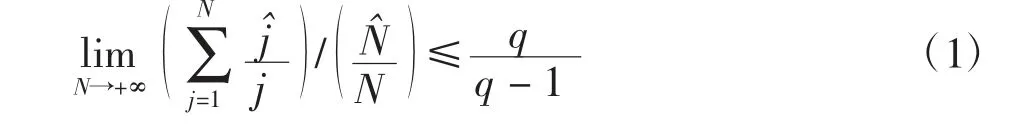
对j≥1，记由

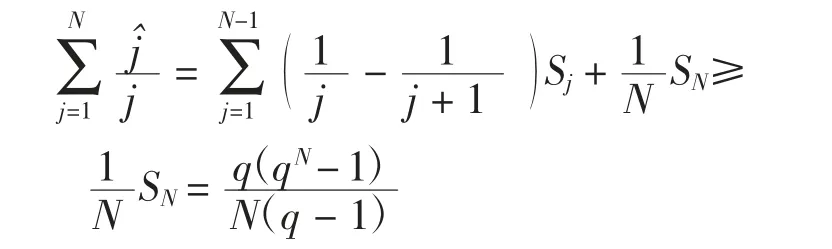
可得

∀1＜λ＜q，注意到，当x≥λ时，x-1≥（1-1/λ）x，所以有

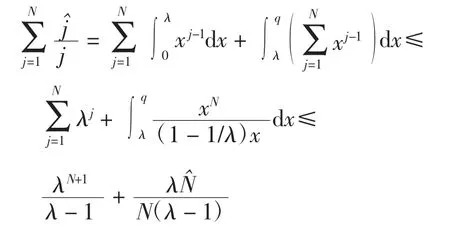
因此

由λ的任意性可得

综上可知式（1）成立.引理结论得证.

引理3 设a、b∈A{0}，且degb≥1.如果（a，b）=1，则

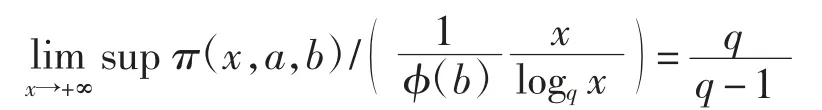
证明对x≥1，存在唯一的Nx∈N，使得因此，由引理2可得

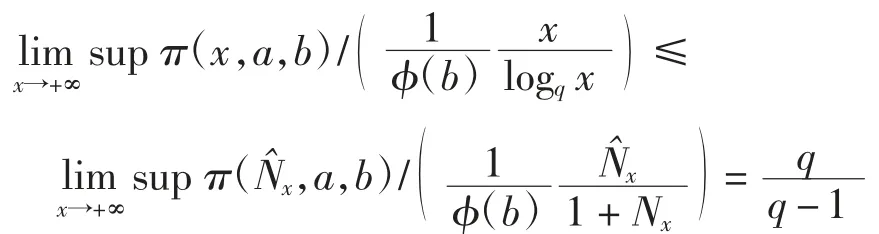
再由引理2可知引理结论成立.

引理4 设a、b∈A{0}，且degb≥1.如果（a，b）=1，则

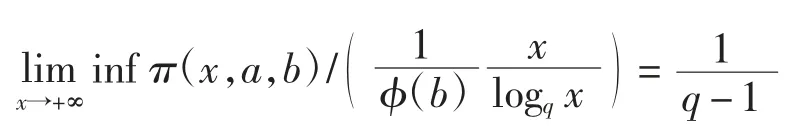
证明对x≥1，存在唯一的Nx∈N，使得因此，由引理2可得

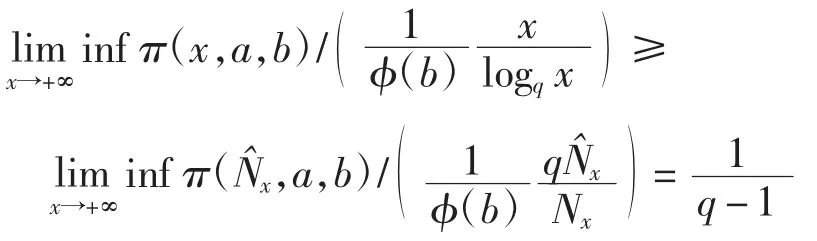
对N∈N，记则由引理2可得

综上可知引理结论成立.

定理3的证明结论（1）是引理3与引理4的直接推论.下面证明结论（2）.

当η=1时，由引理2，取数列为{}即可.当η=1/q时，由引理4的证明可知，数列满足要求.现在假设1/q＜η＜1.

对N∈N+，定义则由引理2可得定理证毕.

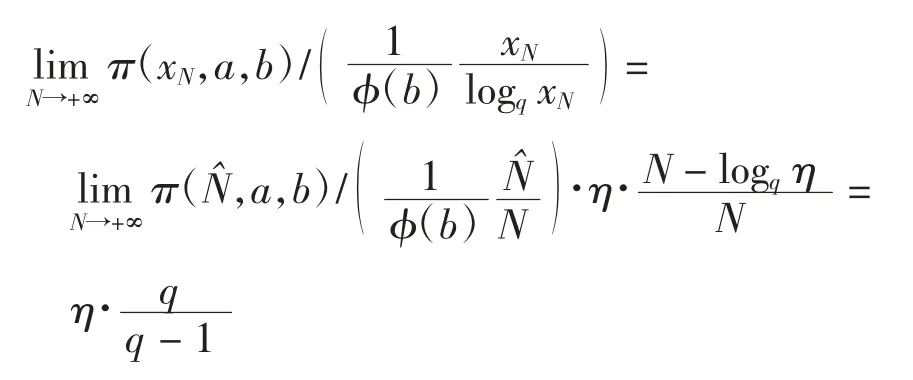
对x≥1，定义π（x）=|{ω∈Ω：|ω|≤x}|.由文献[3]中关于多项式的素数定理，应用与引理2类似的证明方法可得引理5.

引理5 数列{Nπ（Nˆ）/Nˆ}是收敛的，并且

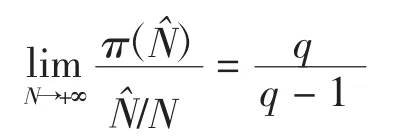
定理4的证明对x≥1，存在唯一的Nx∈N，使得由引理2和引理5可得

定理证毕.

引理6 存在仅与q有关的常数L≥1，使得当x≥L时，有

证明由定理3和定理4可得

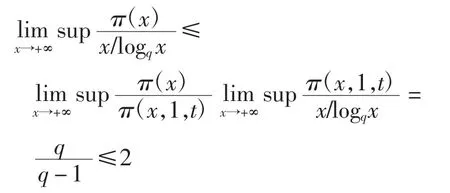
由此可知引理结论成立.

命题∀ε＞0，存在仅与q、ε有关的常数T，使得对a∈A{0}，当|a|≥T时，有D（a）≤|a|(1+ε)ln2/lnln|a|.

证明设a∈A{0}，不妨设a是首1的，且|a|≥存在l∈N+，两两不同的ω1，…，ωl∈Ω，以及α1，…，αl∈N+，使得定义函数λ（x）：（1，+∞）→R为

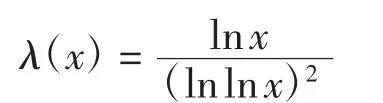
引入记号

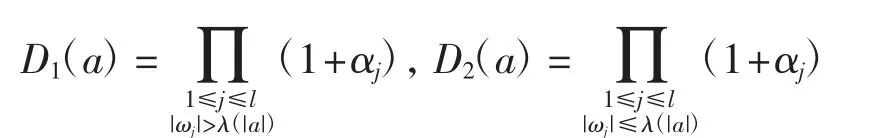
于是D（a）=D1（a）D2（a）.记

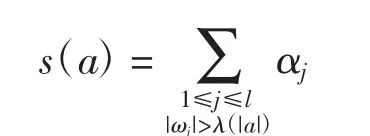
由

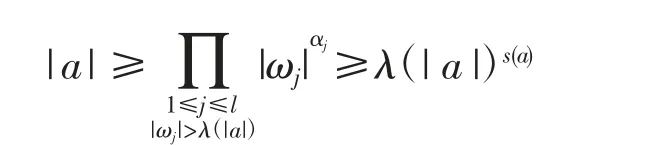
可得s（a）≤ln|a|/lnλ（|a|）.注意到1+αj≤2αj，则有

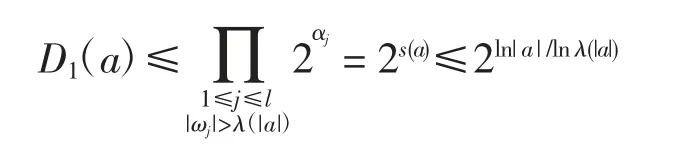
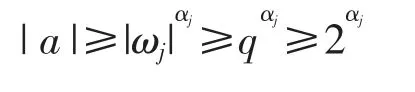
可知αj≤ln|a|/ln 2，再由可得

由引理6，当|a|≥T′时，有

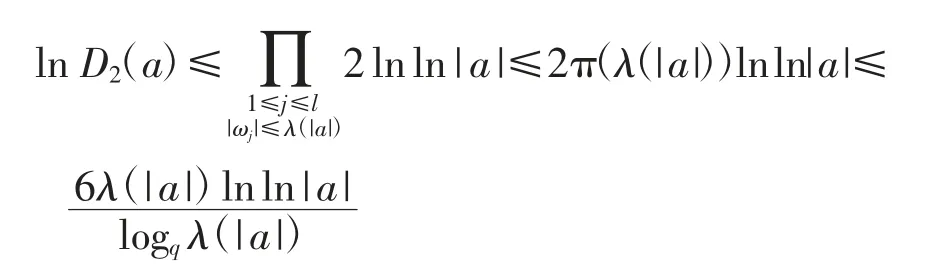
定义函数μ（x）：（T′，+∞）→R为

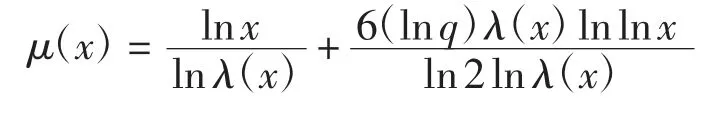
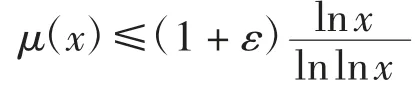
因此，当|a|≥T时，有

命题证毕.

定理5的证明因为，故存在ε0＞0，使得（1+ε0）ln 2＜1.对ε0应用命题即可.定理证毕.

推论的证明存在仅与q、ε有关的常数M″≥M，使得对一切x≥M″，有.因此，由定理5，当|a|≥M″时，有D（a）≤|a|1/lnln|a|≤|a|ε.另一方面，当|a|≤M″时，有

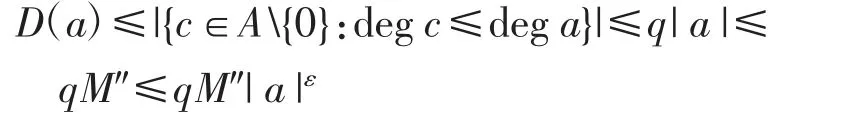
因此，取M′=qM″即可.