一类扩散模型下绝对破产概率的最小化

陈 龙，王秀莲

（天津师范大学数学科学学院，天津300387）

破产理论在保险精算领域中占有重要地位[1-4].近些年，再保险作为保险公司进行风险转移的一项必要措施，引起相关学者的广泛关注，再保险与投资决策成为目前的热点课题之一，其研究成果十分丰富[5-12].文献[5]考虑将盈余投资风险资产和无风险资产，得到了s型最小绝对破产函数及其最优投资策略的显式表达式.文献[6]研究了再保险和风险投资模型的最小化绝对破产概率问题和最大化分红问题.文献[7]基于用跳跃扩散刻画的盈余过程，研究了基于损失规避行为的最优保险投资与再保策略选择，得到了最优投资和再保险策略的解析表达式.文献[8]研究了投资和再保险策略下保险公司的最优合并时刻问题.文献[10]考虑在相依风险模型的框架下保险公司的最优投资和再保险问题，得到最优时间一致的投资和再保险策略以及相应的最优值函数.文献[11]研究了CEV模型下的最优投资和再保险问题.文献[12]研究了保险市场和金融市场具有相依情形下的投资和再保险问题.

本文基于纯扩散模型，考虑将盈余投资于Black-Scholes风险资产和无风险资产，同时可以购买比例再保险.以盈余达到一定的负值定义破产，得到破产概率对应的HJB方程，通过划分不同的控制区域，在每个控制区域上分别求解HJB方程，从而得到最小绝对破产概率的显式解及相应的投资和比例再保险的最优策略.

1 模型建立

没有投资的盈余过程可用扩散近似模型刻画[13-14]，保险公司的动态盈余为

其中：Rt为保险公司在t时刻的盈余；x为初始盈余；c＞0为保险公司单位时间的保费收入；σ＞0为与赔付风险有关的常数；ω(0)为一个标准的布朗运动.设保险公司将盈余的一部分a投资于Black-Scholes风险资产，即

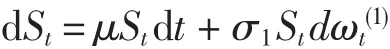
其中：St=a；ω(1)为一个独立于ω(0)的布朗运动；μ＞0为风险投资收益率；σ1＞0为与投资风险有关的常数.盈余St-a投资于无风险资产，即

其中：Bt=Rt-a；r为无风险投资利率.本文假设μ＞r＞0.保险公司为了更好地管理资产，还可以购买一定的比例再保险，设购买（1-b）的比例再保险（0≤b≤1）.在投资和保险控制策略π={a，b}下，盈余动态可表示为

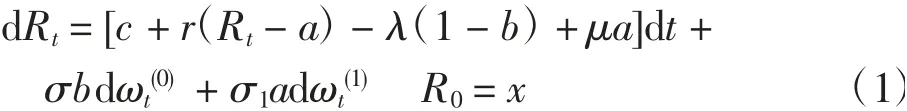
其中λ为再保险公司安全载荷的比例常数，且λ＞c.

设风险投资上界为A≥0，当0≤a≤A，0≤b≤1时，称投资策略π={a，b}为可允许的.所有可允许策略构成的集合记为Π.

在策略π下，初始盈余为x的绝对破产概率Vπ（x）为

为避免破产的发生，保险公司需采取一定的策略，即确定最优策略π*，使得值函数Vπ（x）达到最小，即最优值函数Vπ*（x）为

显然，V（x）是递减的，为方便，设V（x）为C2函数.特别地，当a=0，b=1时，破产慨率可以表示为一个二阶连续可导的积分形式，故V（x）是非平凡的[16].

2 HJB方程

定理1 设V（x）是定义在上的C2函数，且V（x）递减，则最优值函数V（x）满足HJB方程

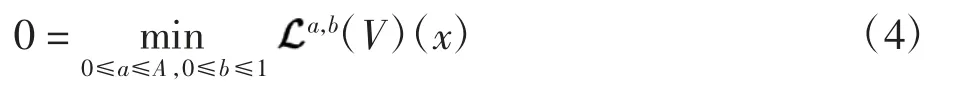
其中

且V（x）满足边界条件（3）.此外，对于所有的x*，若a*（x）、b*（x）满足

则π*={a*（Rtπ*），b*（Rtπ*）}t≥0即为最优策略，即V（x）=Vπ*（x）.

证明令τπM=inf{t＞0：X（t）=M}，τπM，N=τπM∧τπN.由动态规划原理[17-18]可得HJB方程（4）.

因为V（x）是方程（4）满足边界条件（3）的C2解，由文献[5]可得，对于任意-∞＜M＜N＜+∞，τπM，N＜+∞恒成立.取，对V（Rtπ）应用Itô公式可得

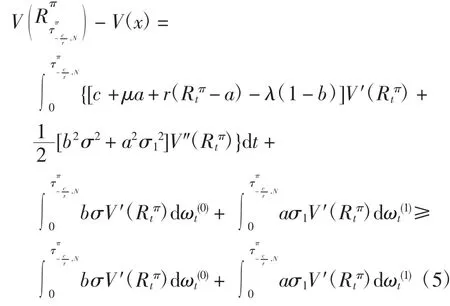
对式（5）取期望得

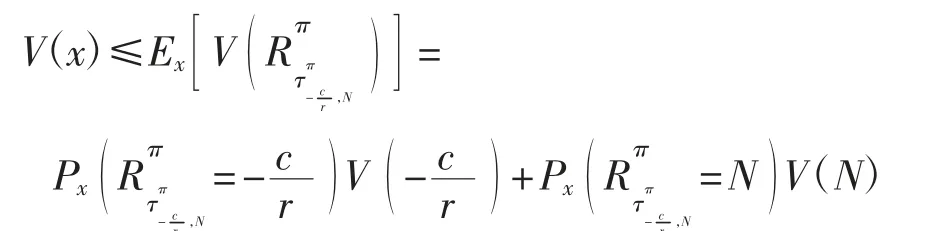
令N→x*，由边界条件（3）可得

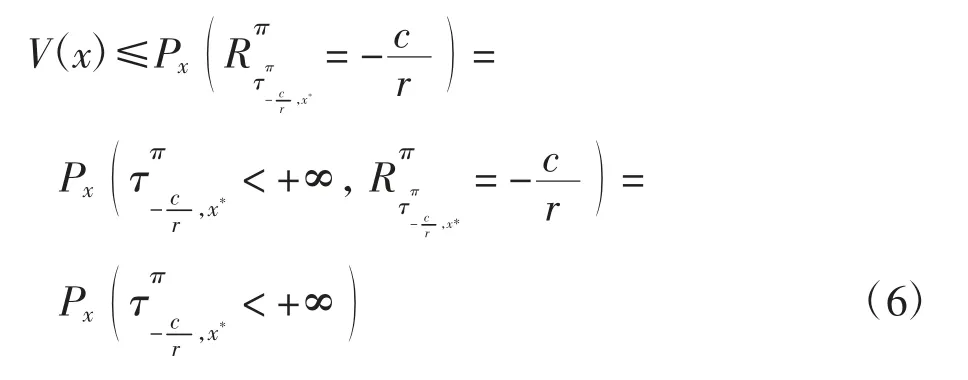
注意到

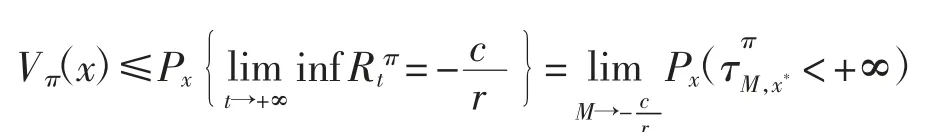
所以V（x）≤Vπ（x）.特别地，当π*={a*（Rtπ*），b*（Rtπ*）}t≥0时，式（5）和式（6）中的不等号变为等号，则有V（x）=Vπ*（x）.

3 最优值函数的解

对方程（4）分别关于a、b求导，可得极值点为

根据二次函数的单调性取不同的控制区域，定义

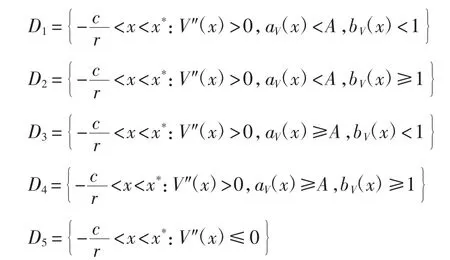
引理1 设V（x）为方程（4）的解，则

（1）在区域D1上，a*（x）=aV（x），b*（x）=bV（x）；

（2）在区域D2上，a*（x）=aV（x），b*（x）=1；

（3）在区域D3上，a*（x）=A，b*（x）=bV（x）；

（4）在区域D4和D5上，a*（x）=A，b*（x）=1.

证明在区域D1上，方程（4）可以看作关于a的开口向上的二次函数，利用二次函数的性质可得a*（x）=aV（x），b*（x）=bV（x）.同理可得区域D2、D3、D4上的结论.在区域D5上，方程（4）可以看作关于a的开口向下的二次函数，利用二次函数的性质可得a*（x）=A，b*（x）=1.

结合引理1和方程（4）可得引理2.

引理2（1）在区域D1上，方程（4）等价于

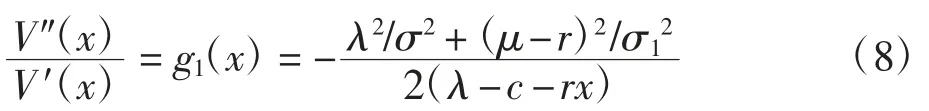
（2）在区域D2上，方程（4）等价于

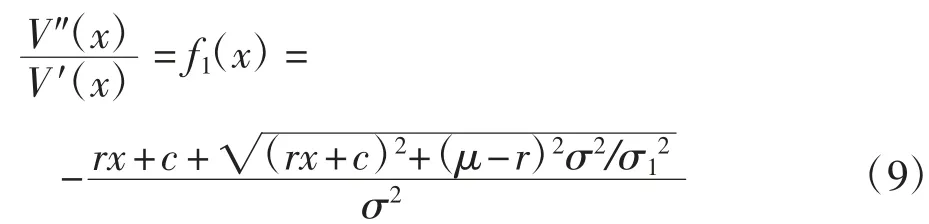
（3）在区域D3上，方程（4）等价于

（4）在区域D4和D5上，方程（4）等价于

引理3 设V（x）为方程（4）的解，则D1=（x1∨x2，x*），D2=（x3，x2]，D3=（x4，x1]，D4∪D5=（-∞，x3∧x4]其中：

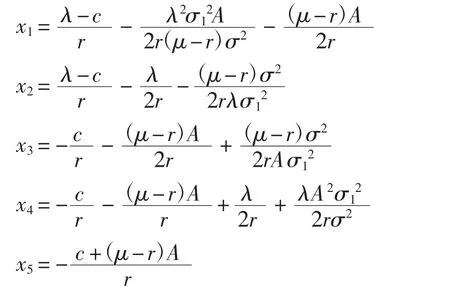
证明在区域D1上，由于V″（x）＞0，所以x＜x*，将式（8）代入式（7）可得

由aV（x）＜A可得x＞x1，由bV（x）＜1可得x＞x2，又x1、x2＜x*，因此D1=（x1∨x2，x*）.同理可得，D2=（x3，x2]，D3=（x4，x1]，D4∪D5=（-∞，x3∧x4）.

由引理3中xi的表达式易得引理4.

引理4 记当μ＞r且A＞时，有x2＞x1，x2＞x3，x4＞x1，x4＞x3.

当μ＞r且时，由引理3和引理4可得由定义区间，通过比较x2、x3与的大小关系可得

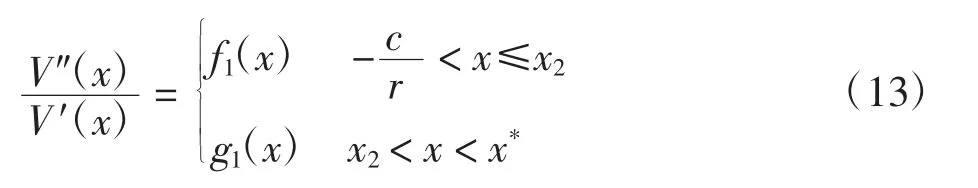
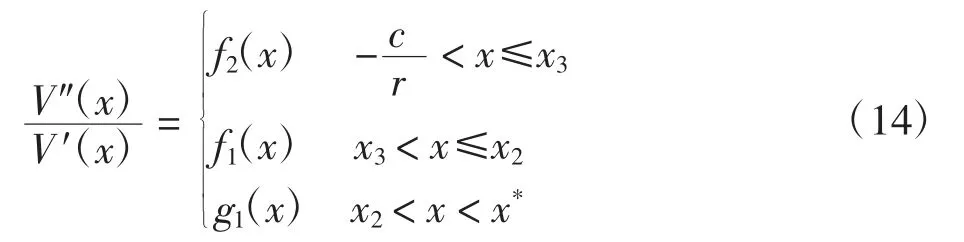
令

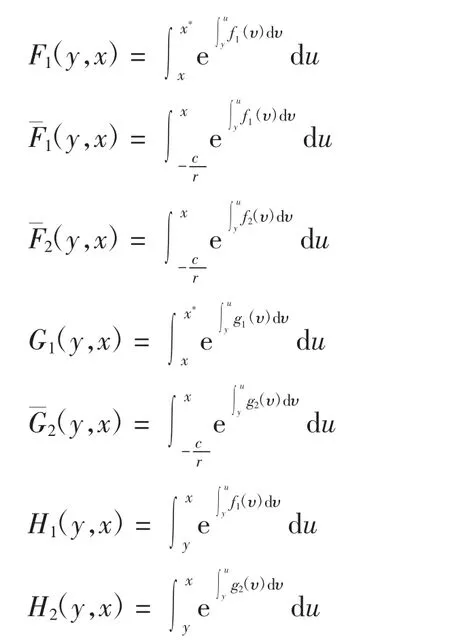
利用边界条件（3）以及V（x）的连续性，分别求解方程（12）～方程（14），可得定理2～定理4.

定理2 当且时，最小化绝对破产概率函数V（x）满足

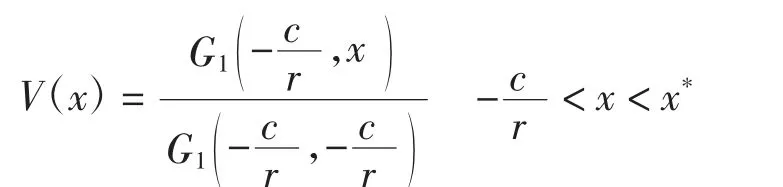
a*和b*分别为

定理3 当且时，最小化绝对破产概率函数V（x）满足

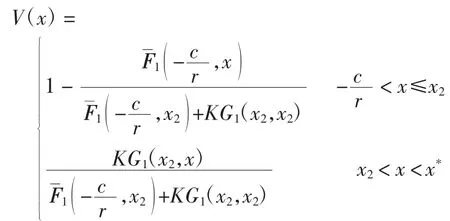
其中a*和b*分别为

定理4 当且时，最小化绝对破产概率函数V（x）满足

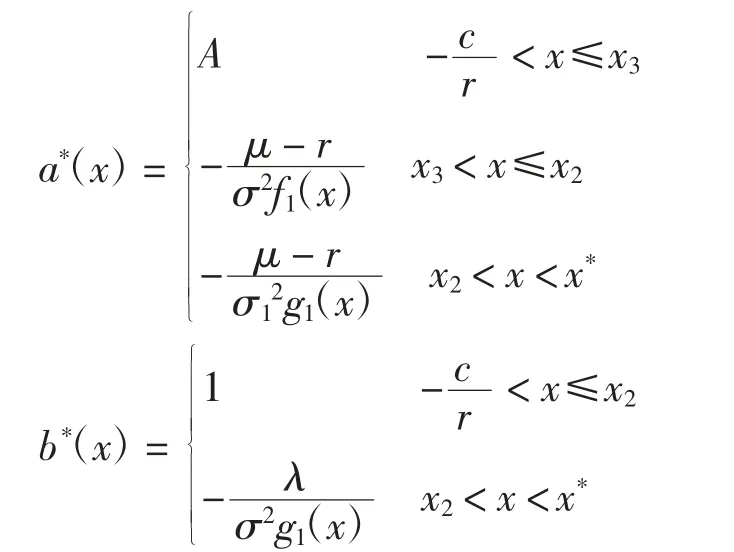
引理5当μ＞r且时，有x2≤x1，x2≤x3，

当μ＞r且时，由引理3和引理5可得D1=由定义区间，通过比较x1、x4与的大小关系可得

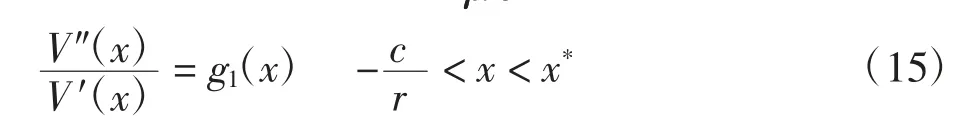
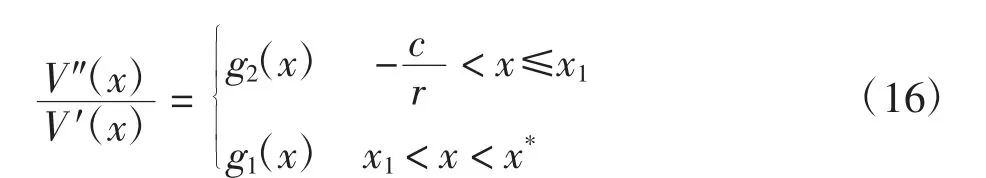
定理5 当且时，最小化绝对破产概率函数V（x）满足

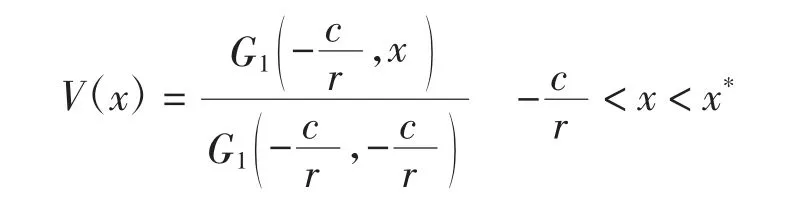
a*和b*分别为

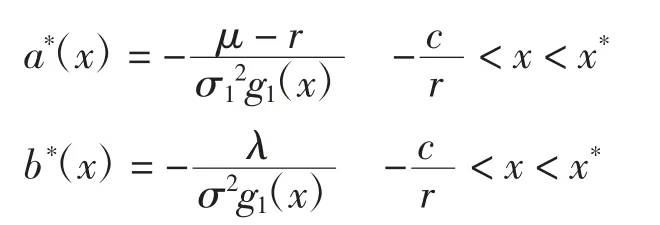
定理6 当μ＞r，且时，最小化绝对破产概率函数V（x）满足

定理7 当μ＞r，且时，最小化绝对破产概率函数V（x）满足

注结合定理4和定理7可以发现，当μ＞r时，最优投资返回函数a*（x）是连续递减的，但随着盈余水平的增加，该策略变得越来越保守，风险投资会越来越少，直到不再购买风险资产；最优比例再保险返回函数b*（x）也是连续递减的，随着盈余水平的增加，购买的比例再保险会越来越多，直到选择100%的再保险.另外，当初始盈余足够大时，保险公司会选择购买100%的再保险而不购买风险资产，此时破产概率为0，与边界条件的分析结果一致.

4 数值模拟

例1 取参数μ=0.2，r=0.1，σ=0.5，σ1=0.25，c=1，A=0.7，λ=1.2，此时有满足定理4，计算得

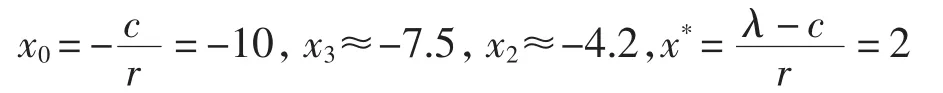
此时V（x）、a*（x）、b*（x）的图像如图1所示.

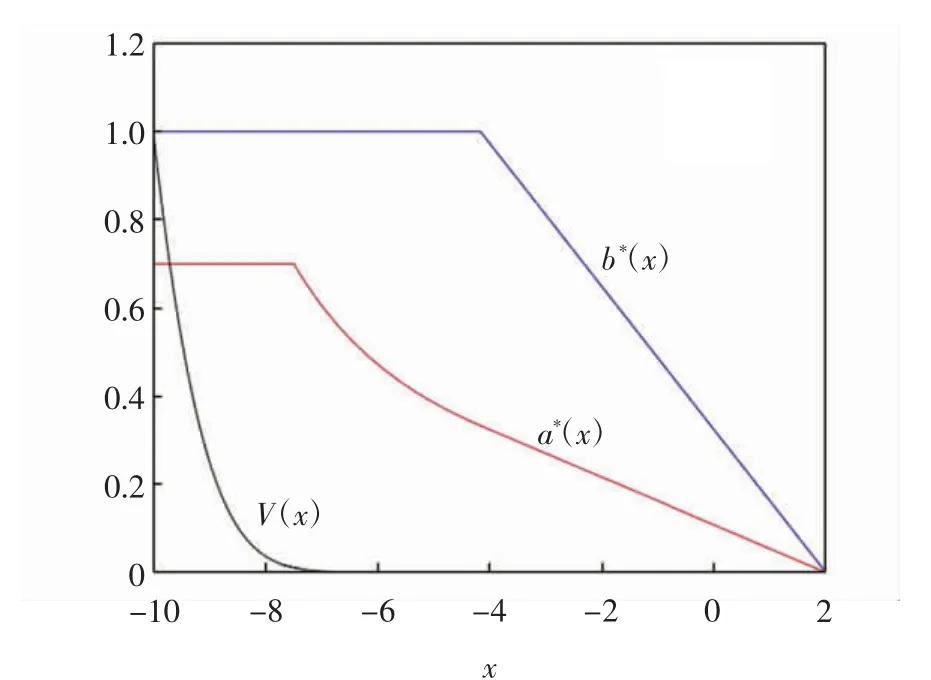
图1 例1中V（x）、a*（x）和b*（x）的图像Fig.1 Images of V（x），a*（x）and b*（x）for Example 1

例2 取参数μ=0.2，r=0.1，σ=0.5，σ1=0.25，c=1，A=0.2，λ=1.2，此时有，满足定理7，计算得

此时V（x）、a*（x）和b*（x）的图像如图2所示.

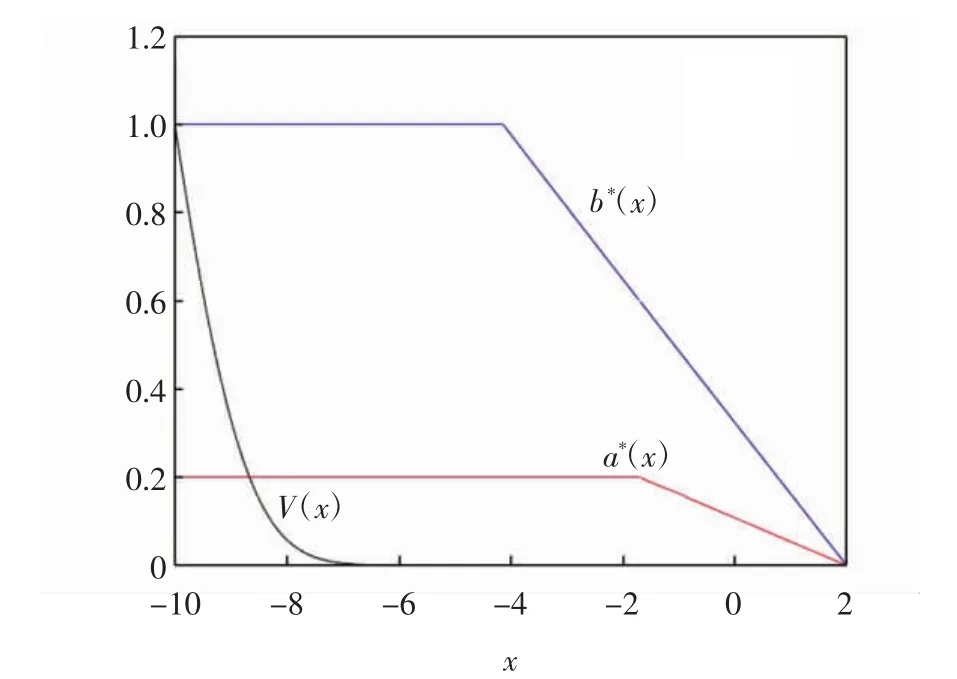
图2 例2中V（x）、a*（x）和b*（x）的图像Fig.2 Images of V（x），a*（x）and b*（x）for Example 2

由图1和图2可见，随着初始盈余的增加，2种情况的绝对破产概率均连续且单调递减；最优投资返回函数a*（x）均先保持一定的水平，在初始盈余达到一定值后，a*（x）变为单调递减函数，即风险投资的数量不断减少；最优比例再保险返回函数b*（x）则先保持自留比例为1，在初始盈余达到一定值后，自留比例会不断减小.