基于正交试验的X80管线钢MIG焊工艺优化∗
侯 阳,李雪芝,周建平,王恪典,2†
(1.新疆大学 机械工程学院,新疆 乌鲁木齐 830047;2.西安交通大学 机械工程学院,陕西 西安 710049)
0 引言
X80管线钢属于低碳微合金钢种,通过复杂的控冷控轧工艺,使其具备了优异的抗延性断裂水平和高强度水平,是目前世界各国输气管线使用的主要钢种[1].近年来,随着X80管线钢的大量使用,其接头质量引起广泛关注,制定合理的焊接工艺,成为管线钢焊接的重要环节.
目前,郭杨柳基于ABAQUS进行了X80管线钢焊接过程应力场的仿真计算,发现焊前热处理会使管线接头外表面和内表面的应力峰值大幅减小[1];张锦洲对X70管线焊接应力及形变程度进行了仿真分析,发现焊接残余变形在初始焊接的内壁处最为显著[2];Wang Lei研究发现2A14-T6铝合金板材的熔合线处和熔合区内的应力峰值随着热输入的增加而增大[3].本文利用正交试验设计方法,研究分析了5 mm厚X80管线钢在不同工艺参数下接头的应力峰值,并采用数值模拟的方法探究了焊接过程及冷却后的应力分布情况,为生产中的管线钢焊接提供参考.
1 试验方案设计
1.1 试验方法
试验采用MIG焊(熔化极惰性气体保护焊),并且用纯氩气来保证热源稳定,整个焊接的过程由松下TA1800焊接机器人完成.使用的焊接填充材料为ER50S-6焊丝,丝径为2 mm.焊件为管线工程中常用的X80管线钢,尺寸为250 mm×100 mm×5 mm(长×宽×高),采用对接焊方式,氩气的恒定流量为14 L/min.焊接接头处的应力峰值待焊件完全冷却后用应力检测仪来检测.
1.2 正交表的选用
为了全面系统的分析焊接过程中不同参数对接头处应力及焊接结束后应力峰值的影响规律,本文采用正交试验法进行试验.在MIG焊中,焊接速度、坡口间隙、电弧电压以及焊接电流是影响焊接接头成形和质量的四个重要工艺参数,因此对这四个参数建立因素水平表.由于前期进行了改变焊枪移动速度的单因素试验,发现焊接速度V=10 mm/s、电弧电压U=23 V、焊接电流I=154 A、坡口间隙L=3 mm时,接头质量良好,若进行多因素试验,在该组合附近可能存在更优参数组合,所以在选取试验参数时,各因素应在上述参数附近设定水平,具体数据见表1.

表1 MIG焊接工艺参数因素水平Tab 1 Factor level of MIG welding process parameters
在因素水平表确定之后,需选择可满足三水平四因素的正交表.目前常用的L9(34)正交表符合要求,将焊接速度、电弧电压、焊接电流和坡口间隙四个因素依次放在L9(34)表的第2、3、4、5列上[4],将表1数据按照L9(34)正交表要求填入,可以得到表2,焊接试验按表2数据进行.
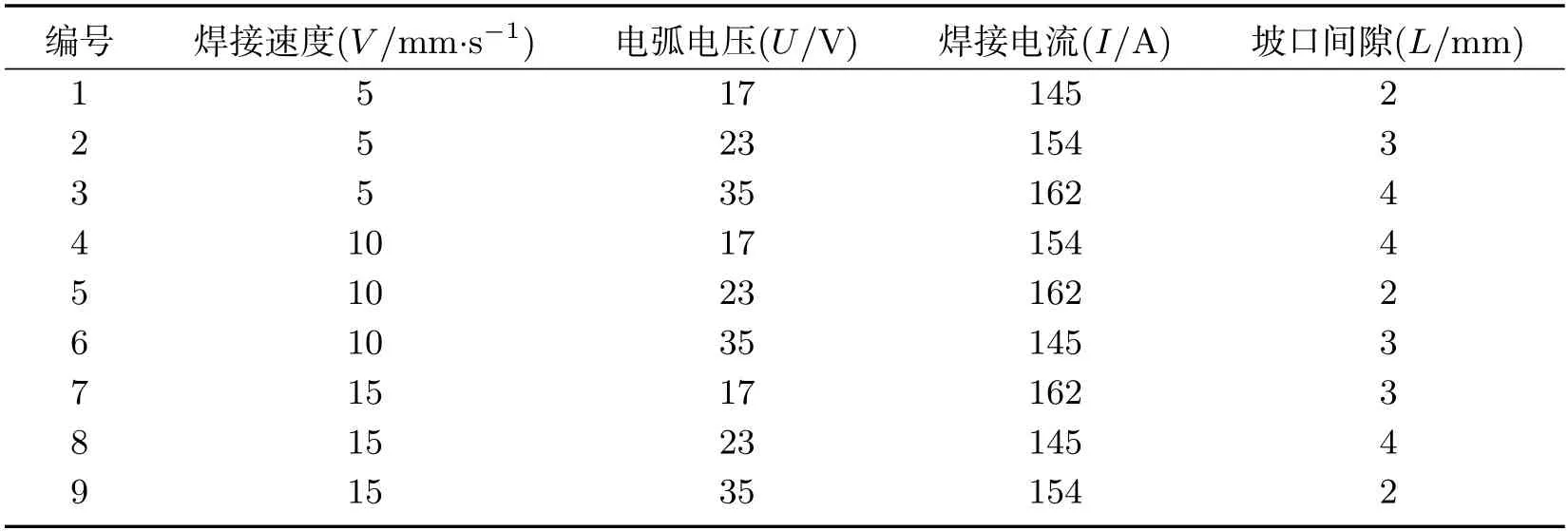
表2 MIG焊接试验参数的正交设计Tab 2 Orthogonal test design of MIG welding process parameters
1.3 有限元模型建立
由于本次试验的焊接模型为对称模型,故只需建立250 mm×100 mm×5 mm的焊接模型,进行焊接温度场仿真时使用SOLID70的三维热分析单元,焊接应力场仿真时使用SOLID45结构单元[5].建立温度-应力耦合场,将温度场数据保存,然后加载到应力场结构单元进行分析.为提高计算效率和准确率,在温度梯度小的地方,网格尺寸划分较大;在温度变化较大的位置,网格的尺寸较细小.本文有限元模型共生成10 954个单元、7 899个节点,最小网格尺寸为1 mm×1 mm×1 mm,所建模型如图1所示.

图1 有限元模型网格划分Fig 1 Finite element model mesh division
由于焊接过程是一个快速而剧烈的热循环过程,为了使所建模型更加准确,需获取X80管线钢随温度变化的热物理性能参数,由文献[6]可获取20~1 200 ℃热物理性能参数,如表3所示,其余参数通过外推法和插值法获取.
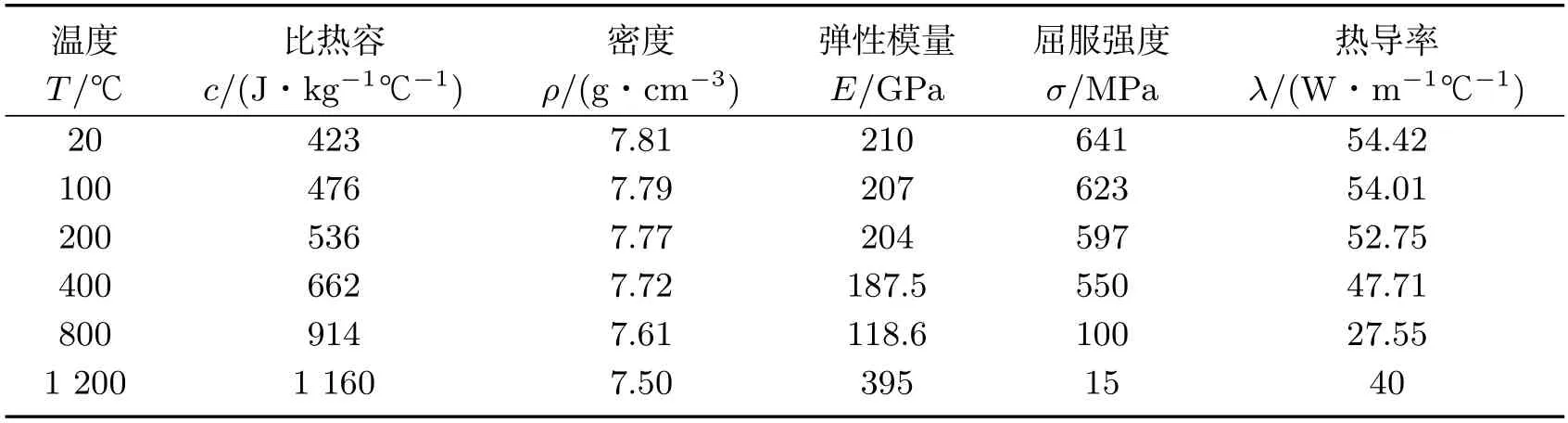
表3 X80管线钢热物理性参数Tab 3 Thermal and physical properties of X80 pipeline steel
1.4 焊接热源及边界条件
焊接热源采用双椭球型热源,使用“生死单元”的方法加载到焊缝,热源在焊缝的移动通过时间步的增加来实现.焊接时的传热主要考虑热传导,同时在热源移动过程中,热量输入集中,导致局部温度剧烈升高,此时在焊件上共存有相变潜热及辐射散热,这是非线性瞬态热传导[7,8].将焊件开始焊接时的温度设定为20 ℃,除焊件焊缝处,其余外表面设置对流散热条件以及辐射散热边界条件,取对流系数为11 W/(m2·K),辐射率为0.8.同时在焊件远离焊缝的两端施加水平和垂直约束,以阻止焊件产生变形和位移[9].
非线性瞬态热传导的控制方程如下[7]:
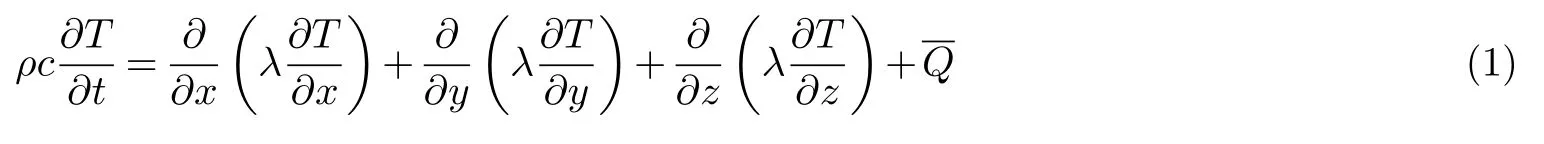
焊件外表面换热边界条件如下[7]:

式中:ρ为材料密度;c为比热容;λ为热导率;Q为内热源密度;a为表面对流换热系数.
2 正交试验结果计算及分析
2.1 极差分析原理
在实践中进行多因素试验时,试验次数繁多,且试验结果难以探寻规律,而正交试验则可将试验次数大幅地减少,并且针对试验结果用合适的分析方法计算,便可找出其规律,并得到有意义的结论,所以被广泛使用,本文使用极差分析方法.
极差分析方法是基于数理统计的方法得出正交表中每个因素的极差R值,R值越大代表影响程度越大,根据R值可确定出因素的排列顺序,然后选出最大的Kij值对应的水平,便为最优的组合.具体计算公式如下[4]:

式中:i为水平数;j为因素数;r为第j因素在相同水平下重复的试验次数;Kij为第i水平下第j因素的试验平均值;Tij为正交表中第j因素在第i水平下对应的评价指标数据的总和;Kij(max)为第j因素的最大值;Kij(min)为第j因素的最小值;Rj为第j因素的极差值.
2.2 焊接试验及极差分析结果
根据表2设计的数据进行焊接试验,焊接结果按表2编号依次排列,如图2所示,可见9组试验所得到的焊缝均成形良好,呈鱼鳞状分布且飞溅较少,焊缝两侧熔合线也清晰可见,整条焊缝无明显缺陷.这是因为表2试验数据都是基于前期改变焊接速度的单因素试验得出,对于后期进行试验有较好的指导性.待焊件冷却后,使用600#的砂纸对焊缝周边进行打磨,直至表面光滑,然后在焊缝附近贴应变片、转小孔,使用JH-30应力峰值检测仪测焊后应力峰值,所得结果填入极差分析表4.

图2 正交试验所得焊缝形貌Fig 2 The weld morphologies obtained by orthogonal test
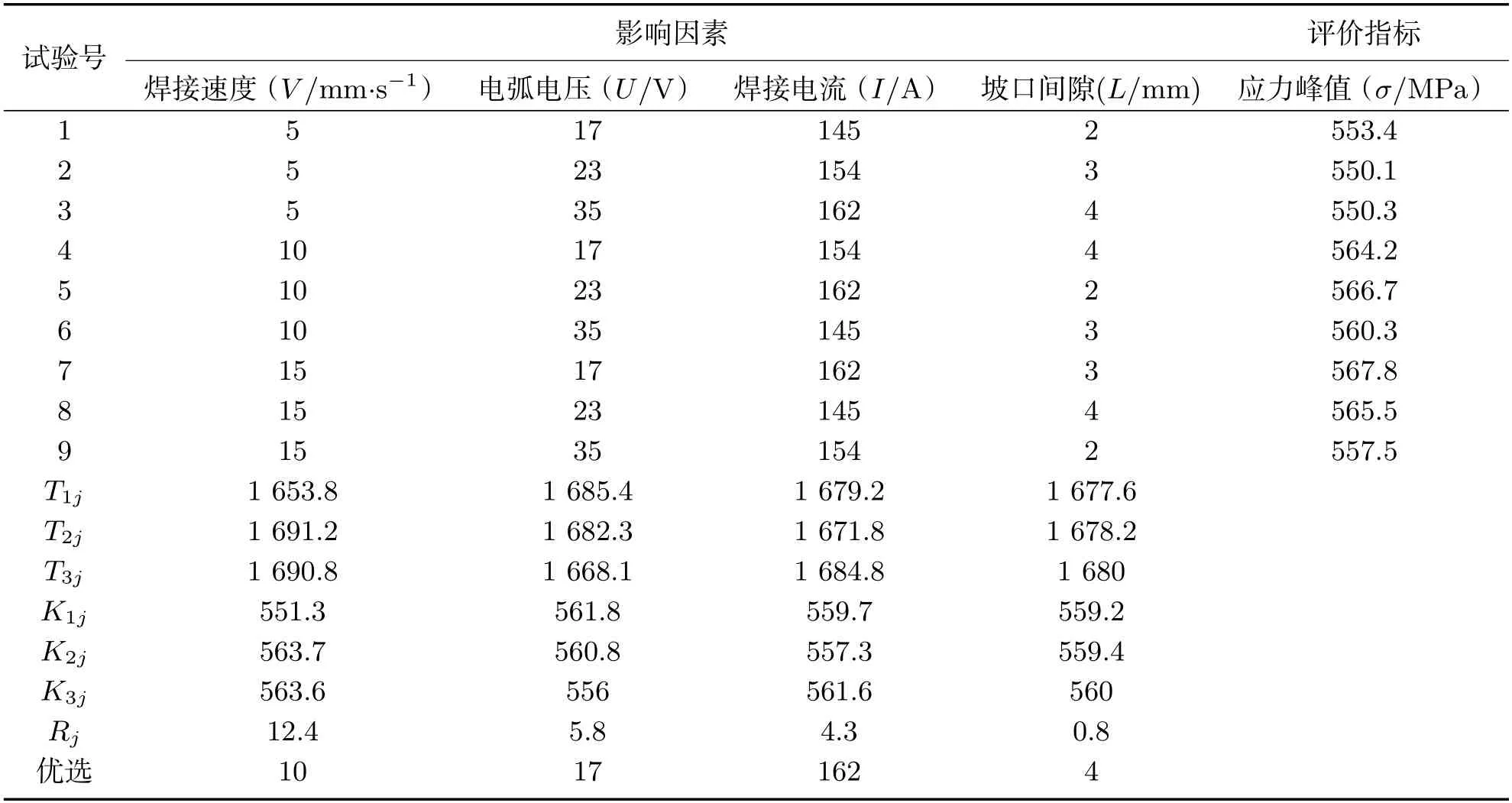
表4 极差分析表Tab 4 Range analysis table
根据公式(3)和(4),代入评价指标数值可得到Kij值和Rj值,见表4.根据所得Rj值可知:R1>R2>R3>R4,即4种因素对焊接应力峰值影响的顺序依次为:焊接速度>电弧电压>焊接电流>坡口间隙.通过比较焊接速度下Kij的值,可知K21>K31>K11,故当焊接速度取第二水平V=10 mm·s−1时,有最小应力峰值;同理比较电弧电压下的Kij值,可知K12>K22>K32,当电弧电压取第一水平U=17 V时,焊接应力峰值最小;比较焊接电流下的Kij值,可知K33>K13>K23,当焊接电流取第三水平I=162 A时,应力峰值存在最小值;比较坡口间隙下的Kij值,可知K34>K24>K14,当坡口间隙取第三水平L=4 mm时,应力峰值最小.所以各因素的最优组合为焊接速度V=10 mm·s−1,电弧电压U=17 V,焊接电流I=162 A,坡口间隙L=4 mm.
3 数值模拟结果与分析
由上述分析可知,正交试验表中未包含最优参数组合,故为验证正交试验优化参数结果是否可靠,本文对上述极差法计算得到的焊接优化参数组合进行了焊接过程的模拟分析.模拟分析中采用的工艺参数为:焊接速度V=10 mm·s−1,电弧电压U=17 V,焊接电流I=162 A,坡口间隙L=4 mm.图3分别是焊接热源移动过程中和焊件完全冷却以后的等效应力云图.图3(a)表示焊接开始,此时应力数值较小,图3(b)表示焊接中间时段,可见焊件两端施加的固定约束已被激活,开始对焊件变形及刚性位移产生约束,图3(c)表示焊接结束.可见在整个焊接过程中,除热源附近分布的应力数值较大外,焊件上其余位置分布的应力数值较小,这是由于焊接过程是一个快速且热量集中输入的过程,熔池熔化,周围应力集中,其他位置则由于热传导作用的衰减,应力作用不明显.图3(d)表示焊件在自然条件下冷却30 min以后的应力场分布,可知在焊件的热影响区和焊缝周围集中分布着横向和纵向的焊接应力峰值,且在焊缝处应力数值达到最大值.

图3 不同时间下焊件的等效应力场Fig 3 Equivalent stress field of the weldment at different time
通过对最优工艺参数组合的模拟计算可知,从焊接开始至结束,焊件上分布的应力最大值为533 MPa,明显小于极差分析表中所有的应力值,表明正交试验选出的参数组合是有效且可靠的.
4 结论
(1)根据正交试验和极差分析法,获得了焊接参数对X80管线钢接头质量的影响规律以及焊接工艺的最优方案.其中接头处的应力峰值主要由焊接速度控制,其次为电弧电压、焊接电流、坡口间隙.
(2)根据正交试验与数值模拟分析的结果,可知X80管线钢MIG焊最优的工艺参数组合为:焊接速度V=10 mm/s,电弧电压U=17 V,焊接电流I=162 A,坡口间隙L=4 mm,此时接头处应力峰值数值最小.
(3)通过对试验分析得出的最优参数组合的模拟计算,发现焊后应力峰值主要集中在X80管线钢的焊缝和热影响区附近,且在焊缝处数值最大,可知在焊缝内部极易产生裂纹.
- 新疆大学学报(自然科学版)(中英文)的其它文章
- On Size,Order,Minimum Degree and Conditional Diameter of Graphs∗
- 给定点数,最小度和条件直径的图的边数的上界∗
- Some Logarithmic Submajorisation Inequalities Related to Heinz Mean∗
- 关于Heinz均值的Log-次优化不等式∗
- Logarithmic Submajorization and Symmetric Quasi-Norm Inequalities on Operators∗
- 有关算子的一些Log-次优化不等式和对称拟范数不等式∗

