高海拔低气压因素对弓网电弧的影响研究

邹丹旦，王梦瑶，项成恩，崔春梅，钟汉华，曾庆建

0 引言

川藏铁路的建设既可以带动西藏地区的发展，也有利于国家的长远发展。该线起始于四川成都市，终止于西藏拉萨市，中途经过雅安、康定、波密、林芝等地，具有地形复杂、海拔高、落差大的特点。线路跨越不同的地貌单元，经过八起八伏，途经海拔高达5 100 m的东达山垭口，累计攀爬高度达1.6万多米。

鉴于川藏铁路所处高寒高海拔的自然环境，其对牵引供电系统的安全可靠性也提出了更高标准要求，其中受电弓与接触网之间的关系在整个牵引供电系统中显得尤为重要[1，2]。弓网系统是电气化铁路目前主要的供能来源，能量供给的可靠性和持续性将影响高原电气化铁路的安全稳定运行[3]。弓网系统运行过程中的升降弓操作、列车晃动、接触导线不平滑和轨道不通畅等因素均会导致弓网离线电弧问题[4，5]。弓网电弧所产生的高温和过电压将严重影响列车的安全运行和受电弓滑板的使用寿命，其产生的感应电磁干扰可能会对电能质量和通信系统造成负面影响[6，7]，严重时甚至会引起重大事故[8，9]。对于在高海拔、低气压环境下运行的高速列车，以正在建设的川藏铁路为例，电弧发生的频率会更高，电弧烧蚀也会更严重，且高海拔环境下弓网电弧的电导、功率等特性参数与低海拔环境下存在显著差别。因此，研究低气压下弓网电弧的电气特性，对于减少电弧的出现以及随之带来的危害具有重要意义。

迄今为止，国内外学者对弓网电弧的发展和电气特性的研究主要集中在高速列车运行的一般环境下[10～12]，并得出了主要结论；对低气压环境下弓网电弧的研究主要集中在运动特性和放电特性上[13，14]。然而，高海拔、低气压等特殊气候带来的电弧频发、电弧电气特性出现显著变化问题及其影响机制尚未研究。因而，深入研究高海拔环境下弓网电弧的特性影响等问题意义重大，这对川藏铁路的建设及后续高寒高海拔地区铁路建设具有重要的参考价值和指导意义。

本文以经典的Mayr电弧模型作为参考，结合列车在高原高海拔地区运行时特殊的自然环境，基于列车运行的速率、电弧耗散功率等因素对高速列车弓网电弧进行建模，根据电弧仿真结果讨论研究高海拔环境下弓网电弧的电气特性。

1 电弧建模原理及模型方程

1.1 电弧数学模型建模原理

本文利用黑盒模型对电弧进行建模研究[15]，只考虑电流终止时内部电路与电弧的相互关系，对电弧的相关特性作如下假设：（1）认为电弧稳定燃炽；（2）将电弧视为一个整体，认为其能够满足一个局部的热力学均衡条件；（3）只对电弧的弧柱部分进行研究。

根据能量守恒原理，电弧微分方程可表示为

式中：dq/dt为单位长度电弧弧柱能量的变化；u·i为单位长度电弧的输入功率，i为电弧电流，A，u为电弧电压，V；ploss为单位长度电弧的耗散功率，W。

将式（1）转换为

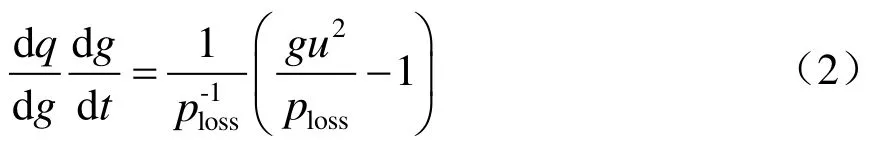
式中：g为单位长度电弧的电导。令电弧时间常数τ为

由上式可得电弧模型的普遍形式：

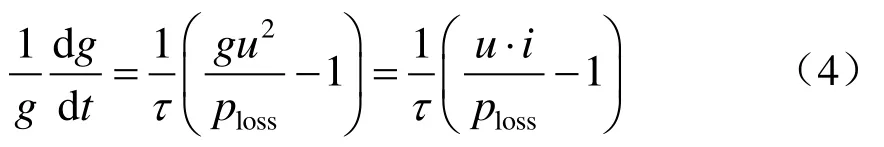
式（4）为黑盒电弧模型的一般数学表达，式中未对电弧时间常数τ和电弧耗散功率ploss作任何限制，因此在不同的假设条件下可推导出不同的黑盒模型。

Cassie电弧模型的模型方程为

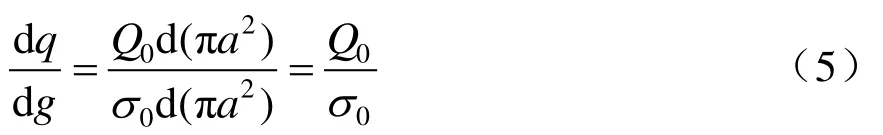
式中：a为电弧半径；Q0为单位体积电弧能量；σ0为单位体积电弧的电导率。

式中：p0为单位体积电弧所散发的功率。

将式（5）～式（7）代入式（3）可得 Cassie模型的时间常数为

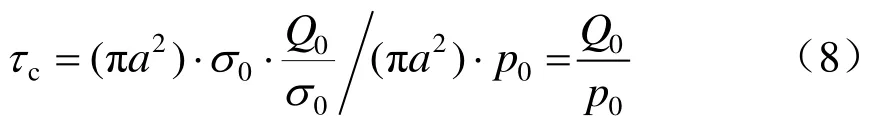
又令

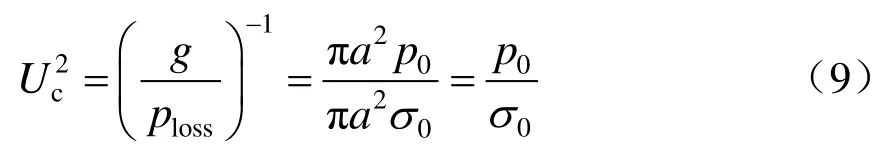
将式（8）代入式（4）并考虑式（1），则有

式（10）即为Cassie电弧模型方程式。其中：τc为Cassie模型的电弧时间常数；Uc为电弧的电压梯度常数。

根据热游离、热惯性和热平衡原理[16]，Mayr电弧模型方程表示为

式中：g0为常数；Q0为单位长度弧柱的含热量；Q为单位体积电弧所累计的能量，J。

式（11）可解释为：当电弧能量改变Q0倍时，电弧电导g随之改变e倍。因为

将式（12）代入式（3）得

Mayr电弧模型的方程式[17]为

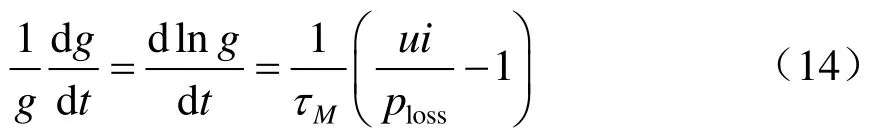
其中，τM和ploss即为Mayr模型的电弧时间常数和耗散功率。

2 弓网电弧模型仿真

2.1 电弧模型搭建

采用 Simulink软件搭建弓网电弧模型，该模型的内电路和外电路如图1、图2所示。电弧模型包括：电压电流测量模块、微分方程编辑器模块、受控源模块、阶跃信号模块和定值检测器模块[18]。

图1 电弧模型内电路

图2 电弧仿真外电路

其中，受控源的作用主要是将电压、电流测量模块输出的电压、电流值传递到外电路。微分方程编辑器（DEE）模块主要用于对电弧数学模型的等效微分方程进行求解，在DEE模块中输入变量和具体的电弧微分方程，并设置相关参数，即可得到输出变量。阶跃信号（Step）模块可以在给定的接触分离时刻产生一个由0到1的阶跃信号，用于控制电弧产生装置接触、分离的起始时间。定值检测（Hit Crossing）模块用于对时间步长进行调节，从而检测仿真过程中电弧电流的过零点。当弓网电弧发生时，及时检测到电压电流的过零点时刻是保障仿真结果可靠的重要前提。

在 Simulink软件中搭建电弧仿真的外电路，将电弧模型一边串联接入交流电源和电阻，另一边与电流测量模块和电压测量模块相连，并接入示波器对电弧电流及电压进行测量，从而显示波形。

2.2 模型实现原理

电弧仿真电路断开时产生弓网电弧，因此本节利用断路器的开断对弓网电弧现象进行近似模拟。在 Simulink软件中，将弓网电弧的模型方程与Mayr电弧模型方程联立，输入到微分方程编辑器（DEE）中实现弓网电弧外部特性的模拟，即

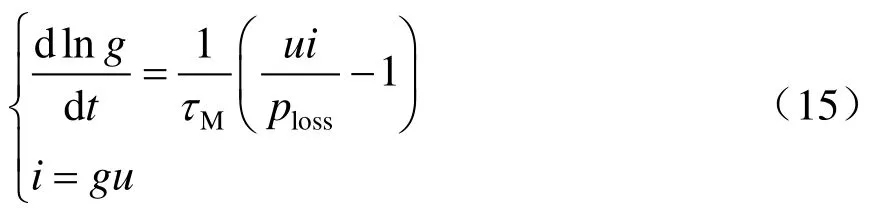
只需在DEE中输入如下形式的方程：

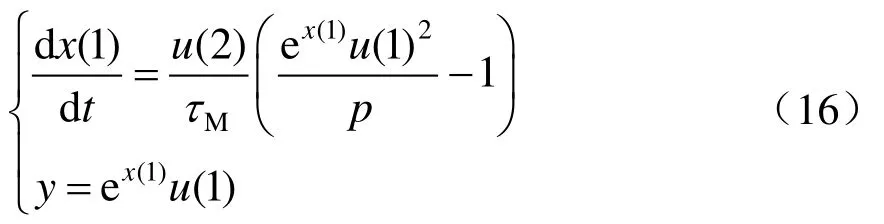
式中：x(1)为微分方程的状态变量，x(1) = ln(g)（g= ex(1)），即电弧电导的自然对数；x(0)为状态变量的初始值。在该式中，x(0) =g(0)，表示电弧电导初始值。

微分方程编辑器模块中有两个输入量：其一为电弧电压u(1)；其二为阶跃信号u(2)，用于调节接触网与受电弓之间接触分离的动作时刻，当接触网与受电弓两者接触时，u(2) = 0，此时无弓网电弧产生，当两者分离时，u(2) = 1，此时电弧开始产生；DEE模块有一个输出量，即电弧电流y。

当弓网之间处于接触状态（u(2) = 0）时：

此时，无弓网电弧产生，电弧模型展现出电导的特性，其值为g(0)，即x(0) =g(0)。电弧未形成时，g(0)为电弧产生装置中接触电阻的倒数，该值可以在DEE模块的对话框内进行设置。

自弓网之间处于分离（u(2) = 1）时刻起，电弧电导基于电弧模型方程发生改变，Mayr电弧方程从此刻起在DEE中开始计算：

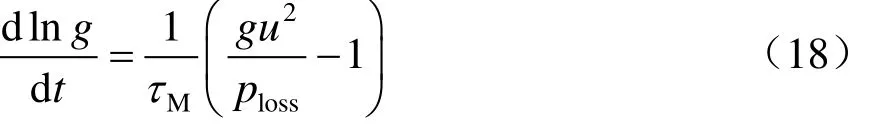
随着时间的改变，此阶段的电弧电导也随之改变。弓网之间分离状态的起始时间可以在电弧模型点开后的对话框中设定。

2.3 弓网电弧模型参数的确定

Mayr电弧模型方程中的主要参数是电弧时间常数τM和耗散功率ploss，外电路的主要参数是交流电源的电压U、频率f，电压内阻r和负载R。本文假定在一般环境下，即海拔为0 m，气压P0为101.3 kPa时，选取τM= 0.000 1 s，ploss= 300 W，g(0) = 0.1 s，U= 25 kV，f= 50 Hz，r= 0.249 7 Ω，R= 125 Ω[19]得出的仿真结果最合理，因此本文选取上述弓网电弧模型参数进行仿真。

3 高海拔下的弓网电弧电气特性

根据上一节中确定的弓网电弧模型参数得出的电弧电压电流仿真结果，通过改变电弧耗散功率ploss的值，研究高海拔环境下弓网电弧电压电流的变化情况，从而得出电导及功率的变化曲线。

文献[20，21]表明，气压P与海拔H的关系为

其中，P0为平原地区的大气压，P0= 101.3 kPa，不同海拔高度下的气压可通过式（19）计算得出。

文献[22，23]提出，当气压降低时，电弧半径随之增大，气压P与电弧半径ra的关系式为

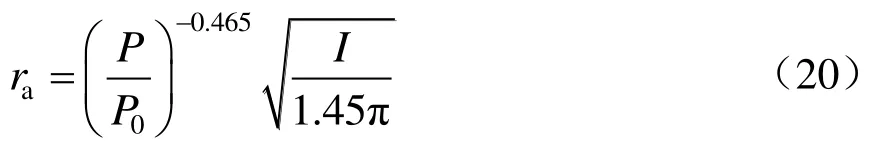
式中：ra为电弧半径，cm；I为电弧电流，A。

由文献[24]可知，当列车运行速率为v时，电弧半径为ra，电弧耗散功率的计算式可表示为

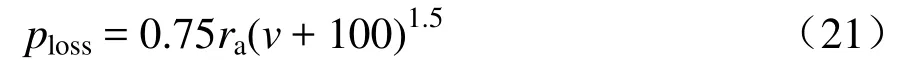
设置海拔分别为0，4 000，4 500，5 000 m，列车运行速率v根据实际情况取值200 km/h，I=0.193 5 A。根据式（19）—式（21）计算出不同海拔对应的气压及弓网电弧耗散功率如表1所示。

表1 弓网电弧参数

根据仿真结果，得到海拔对弓网电弧电压的影响如图3所示，海拔高度H分别取0，4 000，4 500，5 000 m。

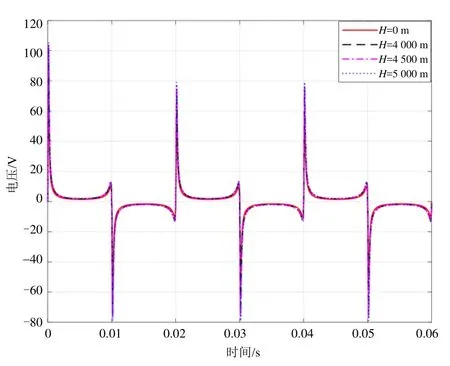
图3 弓网电弧电压曲线

从图中可以看出，随着海拔的升高，电弧电压在燃烧至熄灭的整个燃弧过程中幅值同步增大，其中燃弧尖峰变化最为明显。图4所示为电弧电压在第2个周期（0.02～0.025 s）时的燃弧尖峰曲线。

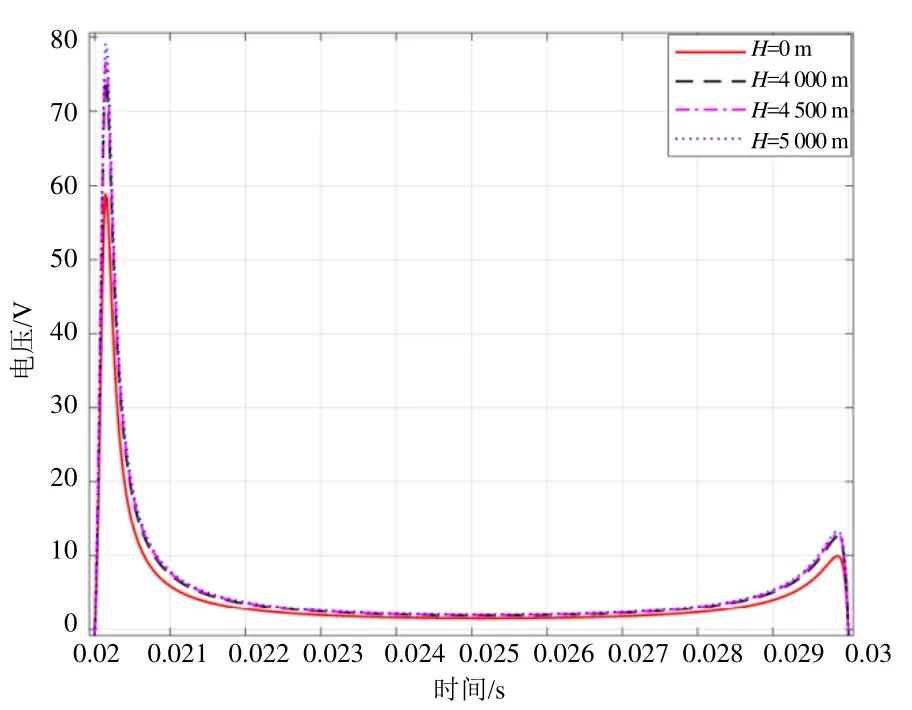
图4 弓网电弧电压燃弧尖峰曲线

在第2个周期中，平原地区的电弧电压燃弧尖峰约为 58 V，随着海拔升高，燃弧尖峰也逐渐拉升，海拔高达5 000 m时燃弧尖峰达到78 V左右，与平原地区燃弧尖峰相差约 20 V；之后电弧电压快速下降并趋于稳定，稳定阶段的电弧电压随着海拔的升高变化不明显。

由电压电流曲线，可得到不同海拔下弓网电弧电导和功率的曲线，如图5、图6所示。

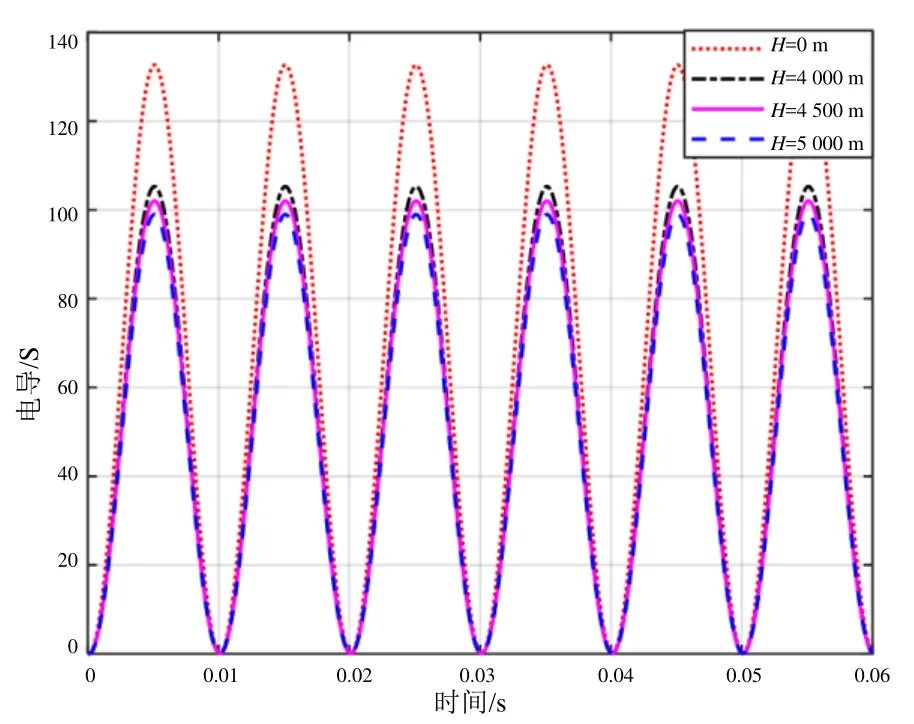
图5 弓网电弧电导曲线

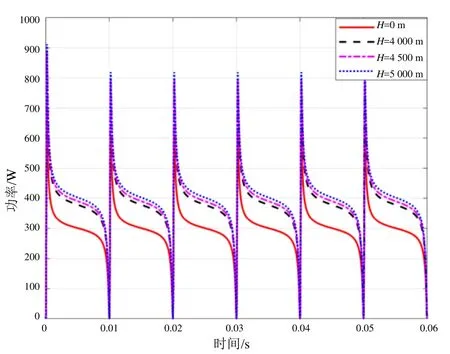
图6 弓网电弧烧蚀功率曲线

由图中可以看出，随着海拔的升高，电弧电导在燃烧至熄灭的整个燃弧过程中幅值逐渐减小，其中尖峰值的变化最为明显。在平原地区即海拔为零时，电弧电导尖峰值达到132 S，随着海拔的升高，电导尖峰值逐渐降低，当海拔高达5 000 m时尖峰值降低到约100 S，与平原地区的电弧电导尖峰值相差30 S左右。当海拔升高时，起弧阶段电弧功率燃弧尖峰逐渐增大，稳定燃弧阶段功率下降迅速且越来越不平稳。从整体来看，随着海拔的升高，功率的幅值同步增大。

由以上分析可以看出，海拔主要对电弧电压、电导和功率产生影响：在电弧产生的一瞬间，电弧电压有一个突变形成燃弧尖峰，当海拔升高时，起弧阶段电弧电压的燃弧尖峰逐渐增大，稳定电弧燃烧时的电压低于电弧起始阶段的电压；在熄弧阶段，熄弧尖峰也随着海拔升高而逐渐增大。从整体来看，从燃烧至熄灭的整个燃弧过程，电弧电压幅值同步增大；而随着海拔的升高，电弧电流的零休时间不变，电流幅值也几乎不受影响。

此外，在整个燃弧过程中，电弧电导幅值随着海拔的升高而显著减小。电弧功率的变化趋势与电弧电导的变化趋势相反，随着海拔升高，电弧功率在整个燃弧过程中幅值同步增大。瞬时电流和电压相乘得到瞬时电弧的功率，从而导致电弧电导和功率发生上述变化，而电流的变化没有电压的变化明显，两者乘积导致功率主要随电压而变化；电导是电流与电压倒数的乘积，因此，电压的逐渐增大导致电导的逐渐减小。

4 结语

通过采用 Simulink软件对弓网电弧模型进行建模仿真，分析了海拔4 000 m以上高原电气化铁路弓网电弧的电压电流波形及电导和功率曲线，从而分析得到了海拔对弓网电弧电气特性的影响：在整个燃弧过程中，弓网电弧电导随着海拔的升高而显著减小；弓网电弧烧蚀功率随着海拔的升高幅值同步增大，其中燃弧尖峰变化最为明显，将影响接触网和碳滑板寿命，需在接触网参数设计中予以考虑。而且，除高海拔的气压因素以外，高原地区的含氧量及温升等因素也将对弓网电弧的电气特性产生影响，有待以后进行更加深入的研究。