双高箱集装运输线路接触网-受电弓适应性研究

孙立金，时恒明，罗 群，吕青松，刘 畅，乔 维

0 引言

具有低能耗、高效率等优势的铁路运输是交通强国战略的重要组成部分[1]，为连接“一带一路”沿线各国及各区域发挥纽带作用。随着经济的快速发展，迫切需要更为高效的铁路集装箱运能方式，为此，国家制定了推进发展双层集装箱运输规划[2]。由两个高箱叠装的双高箱集装运输不但节约运营成本，同时减少跨国高箱运输更换箱体的步骤[3]，能够大幅提升运输效率。为更好地展现铁路运输优势、发展多式联运，有必要对双高箱集装运输系统进行研究。

受电弓-接触网系统为列车运行提供能量，受电弓将接触网系统中电能传输到列车（受流），为牵引电机提供动力，列车能够安全稳定运行的前提是具有良好的受流质量[4，5]。在取流过程中，受电弓与接触线之间存在一定的接触压力，当接触压力保持合适即匹配的弓网系统动力学特性时，才能保证其受流质量，因此，必须对弓网系统的动力学特性展开研究[6]。对于双高箱集装运输线路如金甬线，接触网导线高度已达到6 680 mm，国内外均缺少在该条件下的弓网系统动力学特性研究[7]。为合理组织跨线运行[8]，对动车组通过双高箱集装运输线弓网适应性问题的研究同样不可忽视。

本文将针对金甬双高箱集装运输线路接触网系统展开电力机车运输时以及动车组跨线运行时的弓网系统动力学特性研究，以弓网系统间的接触力各统计数值分析其适应性。在保证受电弓取流的情况下，选取HXD2B、FXD1（货运机车）及CHR6A（动车组）3种车型所搭载的对应型号受电弓展开弓网受流质量分析，可为双高箱集装运输线路以及跨线运行的弓网适应性研究提供一定参考。

1 模型建立及验证

1.1 接触网模型

准确建立接触网系统模型是进行弓网系统动力学研究的前提条件，接触网建模有两种常用方法：通过计算接触网振动模态的模态叠加法[9，10]和基于空间有限元法的直接建模法[11，12]。由于直接建模法具有建模方式简单、精度高等优点，本文将采用该方法对接触网系统进行建模。首先，根据接触线、承力索以及吊弦间连接关系及边界条件采用欧拉梁单元建立初始接触网模型；其次，通过分模法[13]获取接触网系统的关键节点信息，即完成接触网找形；最后，根据接触网系统的关键节点信息建立仿真初始模型，其中吊弦由于其工作特性使用非线性弹簧单元模拟[14]。

金甬双高箱集装运输线路接触网采用简单链形悬挂方式，结构高度为1 400 mm，其具体参数如表1所示，与文献[7]不同的是将接触网系统张力体系改为15/20 kN。

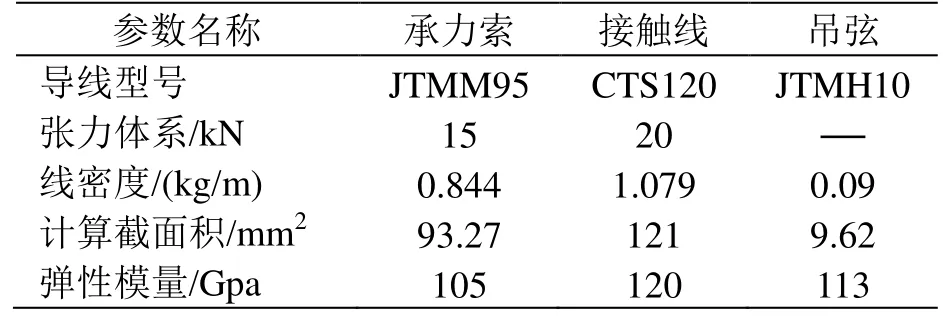
表1 金甬双高箱集装运输线路接触网参数[7]

依照上述建模方法完成接触网系统模型搭建后，接触网的运动微分方程可表示为

式中：M、C、K分别表示接触网系统的质量、阻尼和刚度矩阵，Y表示各单元节点位移组合矩阵，F则为接触网外载荷矩阵。

1.2 受电弓模型

针对不同的研究需求，受电弓建模可处理为不同的模型，其中多刚体系统更接近实际，进而本文将受电弓处理为多刚体系统。受电弓多刚体系统又可分为受电弓弓头部分及框架部分，其中框架部分由下臂杆、上框架、拉杆和平衡杆组成，各杆件之间通过铰接组成只由升弓角θ表示的单自由度系统。框架部分的动力学方程可写为[15]

式中：Ak、qk、Bk分别为框架系统的系数、坐标向量以及广义载荷向量矩阵，Φk为铰接约束方程雅可比矩阵，λk为其对应的拉格朗日乘子。

参考文献[15]，弓头部分的动力学方程可写为

式中：Mh、Yh、Fh分别表示弓头系统的质量、位移和载荷矩阵。

因此，可得受电弓多刚体系统的动力学方程：

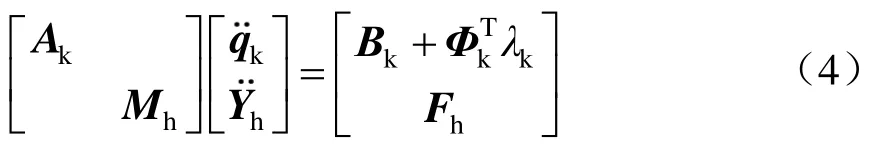
1.3 弓网耦合模型

弓网系统通过接触力耦合，常通过线性接触刚度并结合罚函数法计算接触压力[16]，接触模型及其示意图如图1所示。

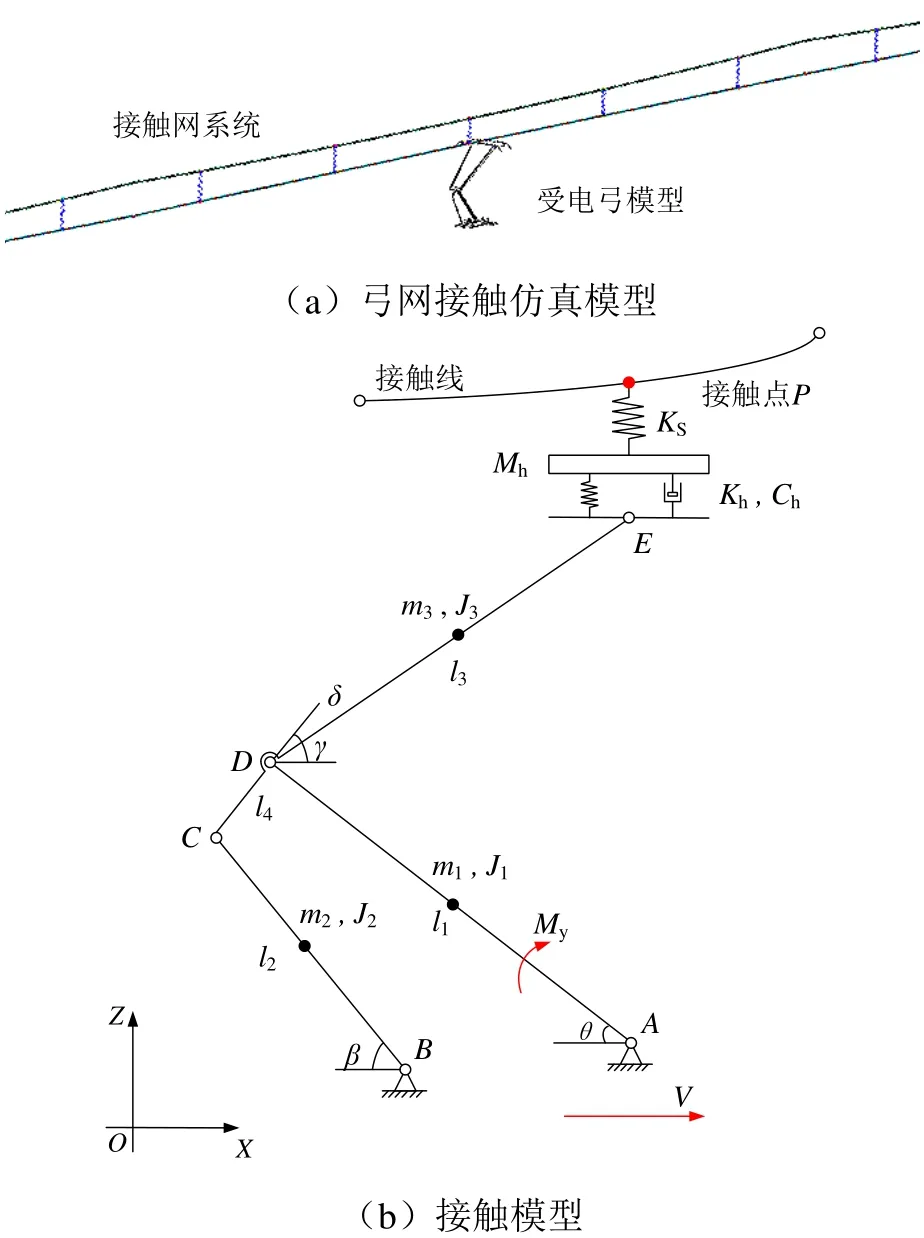
图1 弓网系统接触模型

设接触点P的垂向位移为zc，则接触力可写为

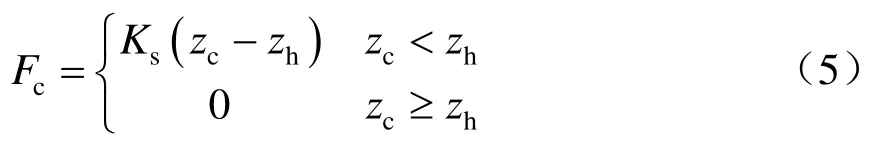
式中：Ks为接触刚度，取50 000 N/m[17]；zh为弓头相对位移。

1.4 模型验证

对于弓网系统仿真，欧洲标准 EN 50318—2018[17]提供了双弓系统仿真模型的建立方法可行性验证，依照本文方法建立该标准中受电弓-接触网仿真验证模型。将速度级275 km/h仿真结果与标准中参考数值进行对比，结果见表2。可以看出，各参数统计结果均在标准范围内，即验证了本文方法的可行性。

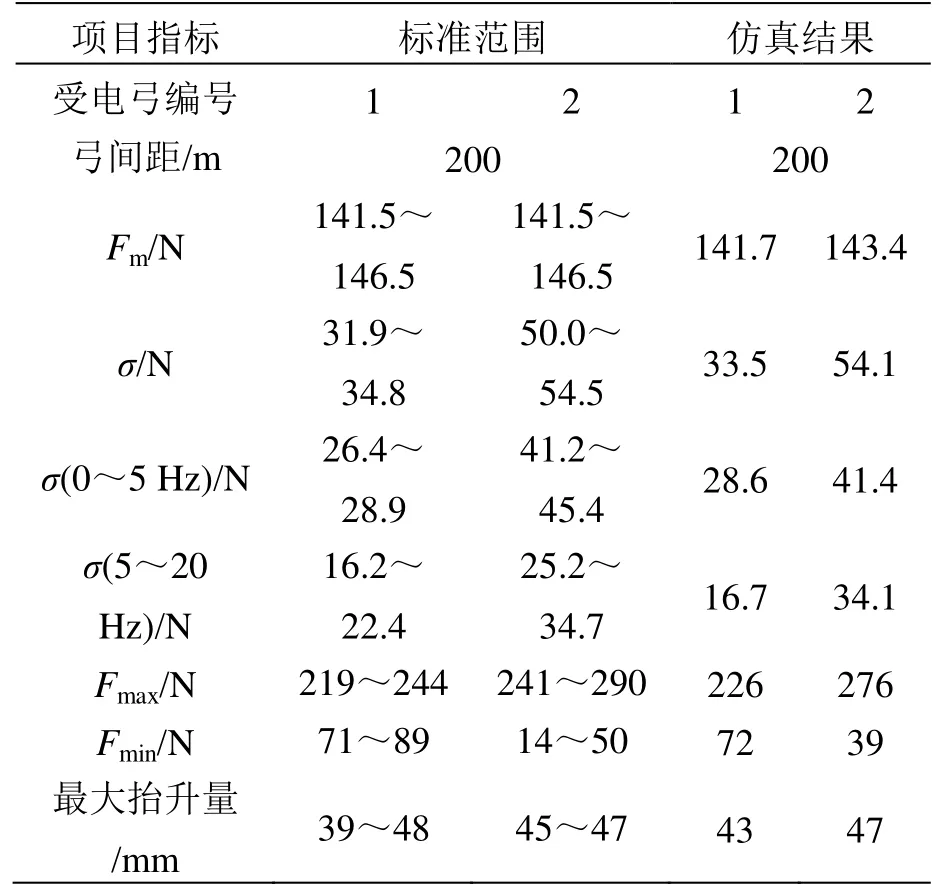
表2 模型验证结果对比

2 仿真结果分析

针对金甬双高箱集装运输线路接触网系统，为分析电力机车如HXD2B、FXD1（货运机车）运输时以及动车组如CHR6A跨线运行时的弓网动力学特性，依据本文建模方法，分别建立接触网模型以及对应受电弓模型进行仿真计算，通过计算结果中弓网系统间的接触力各统计数值分析其适应性。

接触力各统计数值与标准TB/T 3271—2011[18]中指标进行对比，主要包括对接触力均值Fm、标准偏差σ、统计最大值、统计最小值的对比，各统计数值标准指标如下：

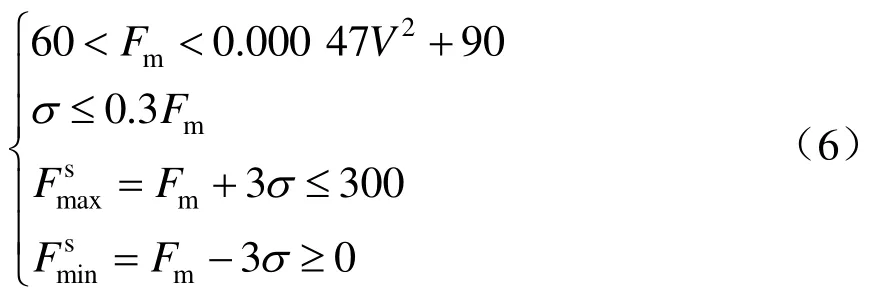
式中：V为运行速度。

金甬双高箱集装运输线路设计时速为160 km，预留时速200 km条件，各车型搭载的受电弓详细信息以及规划计算工况如表3所示，其中受电弓工作高度包含绝缘子高度。

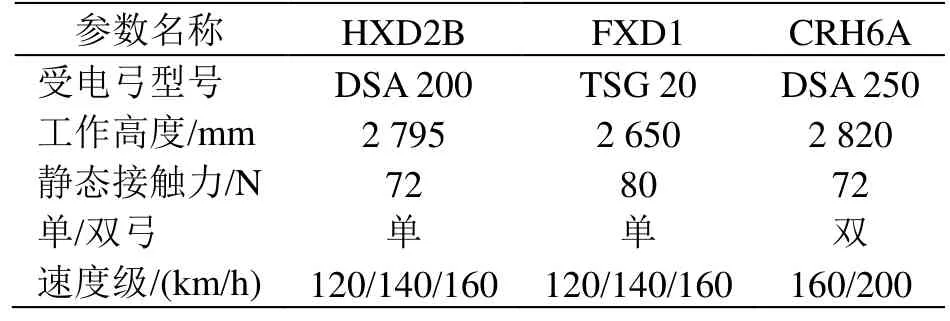
表3 受电弓型号详细信息及计算工况设置

2.1 DSA 200型受电弓仿真结果

由表3可知，车型HXD2B所搭载的DSA 200型受电弓工作高度为2 795 mm，静态接触力为72 N，各速度级仿真结果如图2所示。

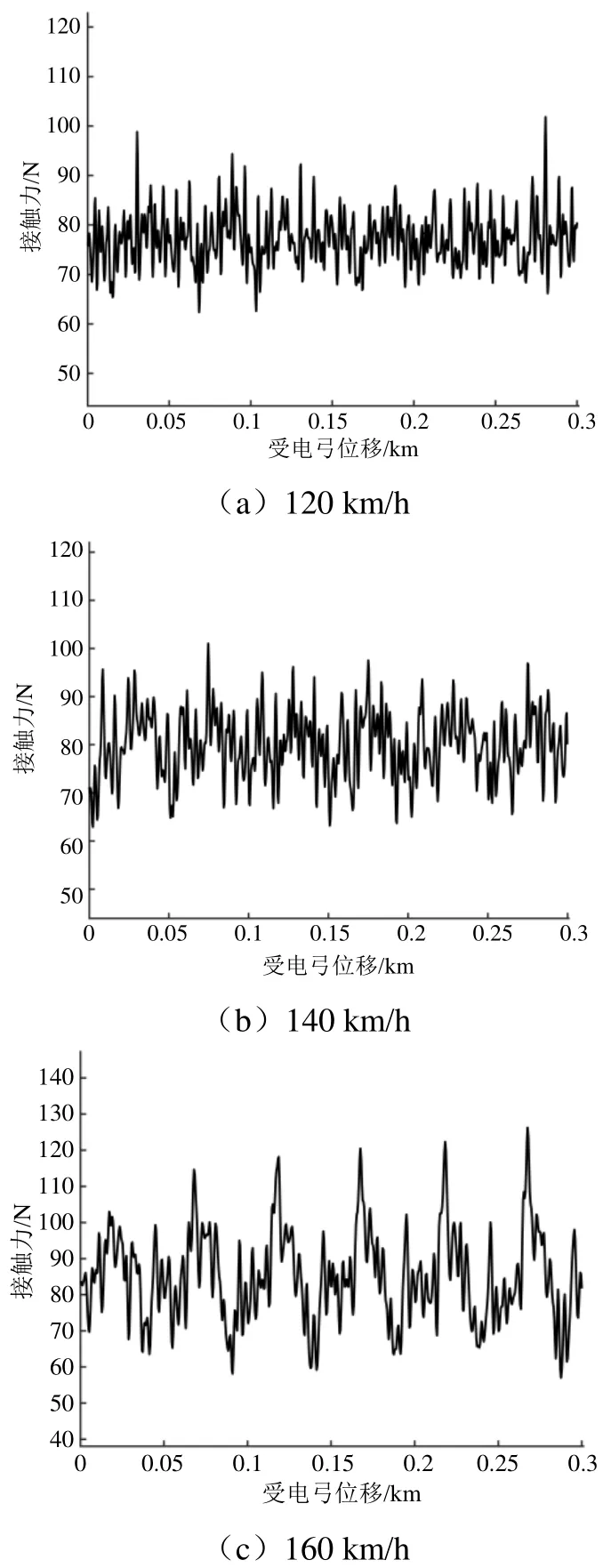
图2 DSA 200型受电弓各速度级仿真结果

将DSA 200型受电弓各速度级下接触力仿真结果进行统计并计算各统计数值，得到表4。可以看出，随着速度级的增加，弓网系统间接触力均值、标准偏差呈现增加的趋势，即受流质量相对变差。同时，对比式（6）各指标，接触力均值、标准偏差、统计最大值以及统计最小值均处于标准范围内，未出现受电弓离线情况，受流质量良好，即 DSA200型受电弓与金甬双高箱集装运输线接触网系统匹配适应性良好。

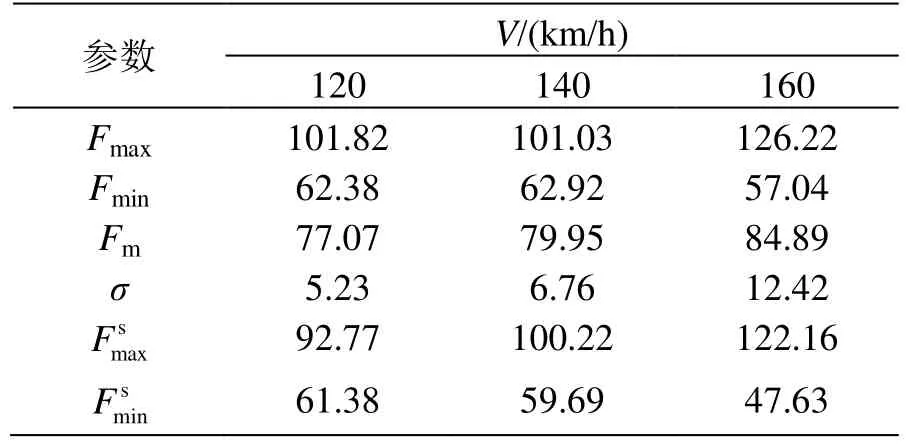
表4 DSA 200型弓网动力学统计值 N

2.2 TSG 20型受电弓仿真结果

车型FXD1所搭载的TSG 20型受电弓工作高度为2 650 mm，静态接触力为80 N，各速度级仿真结果如图3所示。

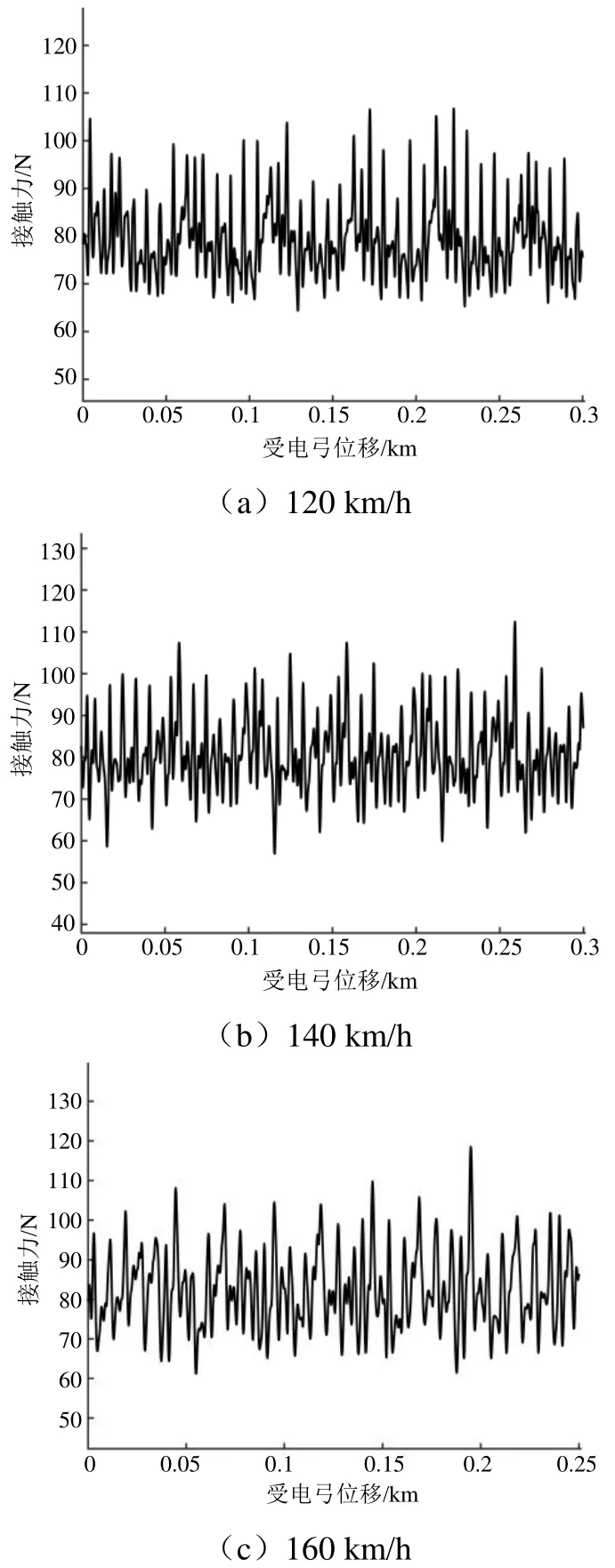
图3 TSG 20型受电弓各速度级仿真结果

将TSG 20型受电弓各速度级下接触力仿真结果进行统计并计算各统计数值，得到表5，其均值、标准偏差也呈现随速度增加而增加的趋势。同样对比式（6）各指标，该型号受电弓弓网动态接触力均值、标准偏差、统计最大值以及统计最小值均处于标准范围内，未出现受电弓离线情况，受流质量良好，即TSG 20型受电弓与金甬双高箱集装运输线接触网系统匹配适应性良好。

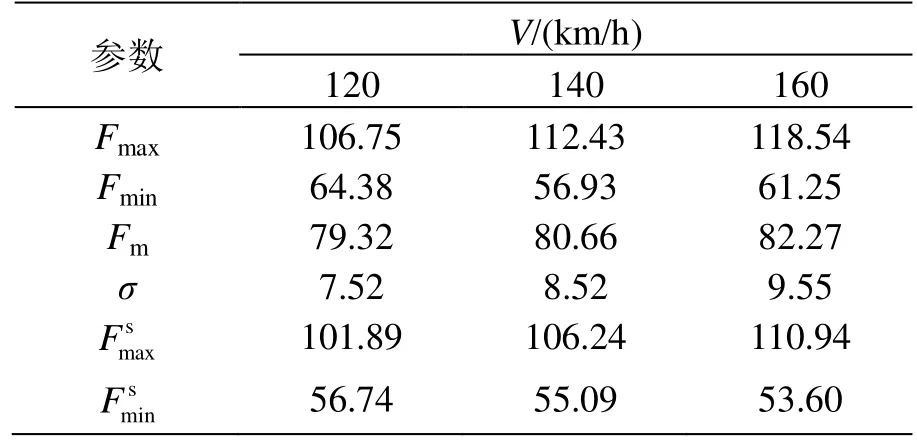
表5 TSG 20型弓网动力学统计数值 N

2.3 DSA 250型受电弓仿真结果

上述已完成两种型号的货运机车搭载受电弓的弓网系统受流质量评估，即金甬双高箱集装运输线路上货物运输车型的弓网关系适应性研究，下文将针对跨线运行动车组 CRH6A车型搭载的 DSA 250型受电弓展开弓网关系适应性研究。根据表3，DSA 250型受电弓在金甬双高箱集装运输线路上工作高度为2 820 mm，且为双弓受流，静态接触力为72 N，其中双弓间距为210 m。各速度级仿真结果如图4所示。

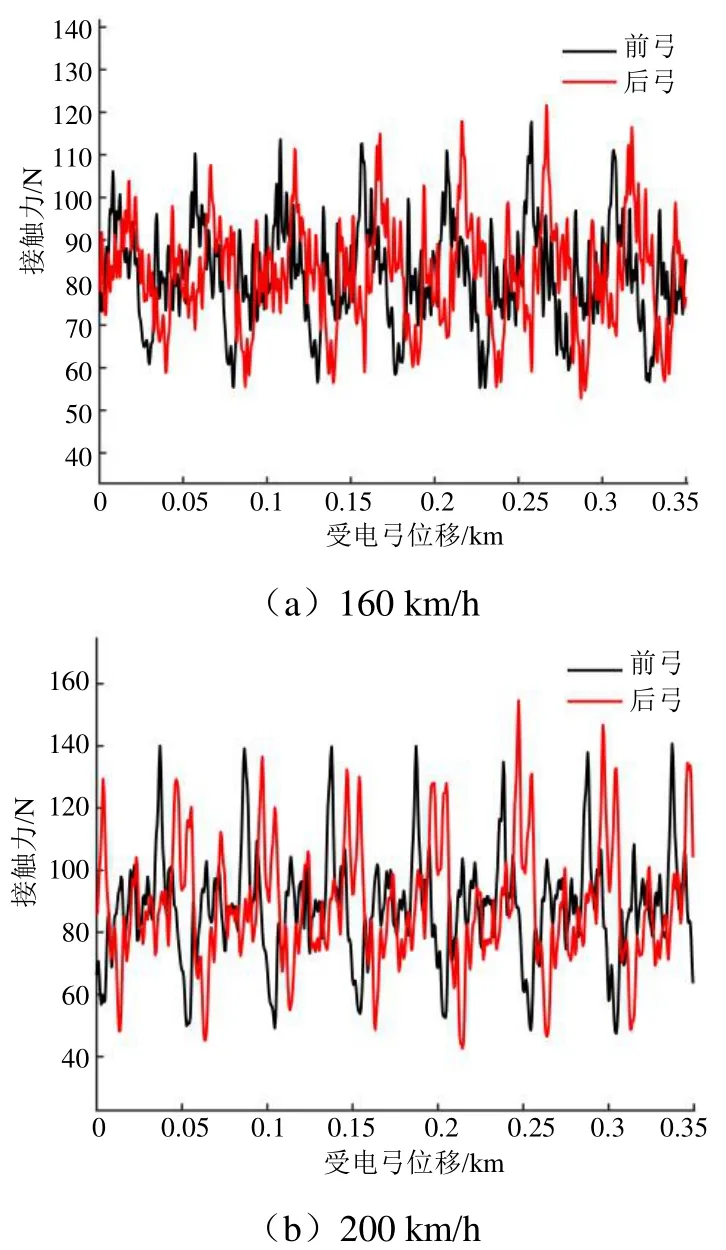
图4 DSA 250型受电弓各速度级仿真结果

获取双DSA 250型受电弓系统各速度级下接触力仿真结果并相应计算各统计数值，汇总得到表6。可以看出：在同一速度级时，后弓接触力均值与前弓基本一致，标准偏差小幅增加，即后弓受流质量稍差于前弓受流；速度级增加时，接触力均值、标准偏差也呈增加趋势，但各统计数值均处于标准范围内，未出现受电弓离线情况，受流质量良好。即DSA 250型受电弓双弓系统跨线运行与金甬双高箱集装运输线接触网系统匹配适应性良好。

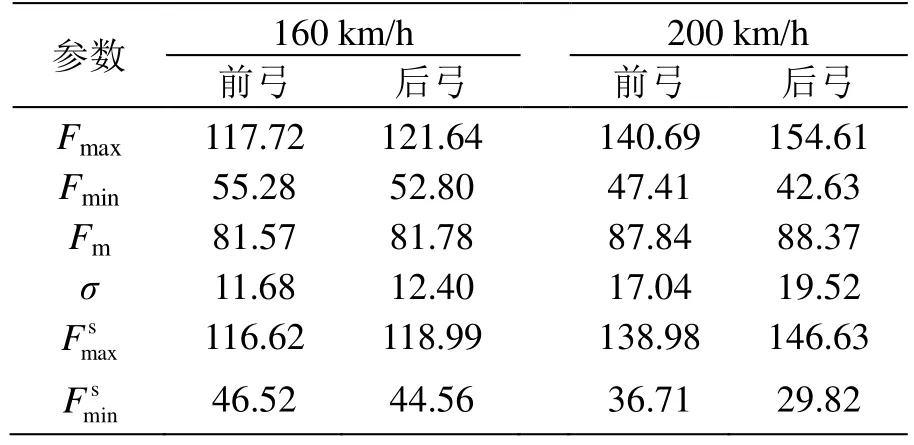
表6 DSA 250型弓网动力学统计数值 N

3 结论

本文对DSA 200、TSG 20及DSA 250型受电弓在单、双弓条件下与金甬双高箱集装运输线路接触网系统的弓网动力学特性进行研究，将弓网间接触力仿真结果各统计数值与相关标准对比，分析其弓网适应性，为双高箱集装运输线路及跨线运行的弓网适应性研究提供一定的理论依据。结果表明：

（1）单弓受流时，DSA 200、TSG 20型受电弓接触力均值、标准偏差均呈现随速度级增加而增加的趋势，即弓网受流质量随速度增加而降低，但各统计数值均处于标准参考值范围内，受流质量以及弓网适应性良好。

（2）双弓受流时，DSA 250型受电弓在同一速度级下，后弓接触力均值与前弓基本一致，但标准偏差小幅增加，即后弓受流质量稍差于前弓受流，不同速度级下接触力均值、标准偏差变化与单弓受流的趋势一致，且均处于标准范围内，前、后弓受流质量及弓网系统适应性均良好。