接触网上方平行接近或交跨高压交流输电线路感应电研究

李正康，高仕斌，周文婕，廖 铭，鲜永辉，韩正庆

0 引言

由于高压交流输电线路走廊的空间限制，在高速铁路接触网上方不可避免出现平行接近或交叉跨越高压交流输电线路的情形[1]。高压交流输电线路电压等级高、线路负荷电流大，在接触网停电检修时，通过静电耦合和电磁耦合作用，在其下方接触网线路上可能会产生较大的感应电压和电流，威胁检修人员的人身安全。为保障接触网检修作业安全，有必要对停电检修状态下的接触网感应电展开研究。

以往的研究主要集中在高压交流输电线路同杆架设或平行接近时停运线路上的感应电压，对低压导体上方平行接近或交叉跨越高压交流输电线路时感应电研究较少[2～6]。针对接触网附近带电运行导体的耦合作用，文献[7]提出了电气化铁路接触网与接触网支柱外侧电力贯通线不同运行条件下的静电和电磁感应电压计算方法。已有的研究尚未系统地涉及接触网上方平行接近或交叉跨越高压交流输电线路时产生的感应电的研究。

本文在分析接触网上方平行接近或交叉跨越高压交流输电线路时感应电的耦合原理基础上，提出利用多导体传输线模型计算停电检修接触网上感应电；考虑到高压交流输电线路在接触网通过的路径各点上所产生的空间电位大小和相位的差异，将接触网进行分段处理，计算每一小段的感应电压和电流，叠加得到接触网上总感应电压和电流；最后利用 Matlab编程计算不同影响因素下接触网感应电的大小，为接触网检修作业安全防护提供参考依据。

1 感应电耦合原理分析

接触网上方平行接近或交叉跨越高压交流输电线路时，若忽略外部带电体影响，接触网导体和输电线路导体可看作多导体传输线系统。多导体传输线系统中正常带电运行导体周围会产生电场，通过导体间的电容耦合作用会在停运导体上产生容性感应电压，并且当正常带电运行导体流过交流电流时，在其周围会产生交变磁场，若停运导体与其交链，则在停运导体上会感应出沿导体方向分布的纵电势。根据停运导体不同对地绝缘状态而对应不同的感应电压[7]，根据感应电流不同的流通路径又可分为容性感应电流和感性感应电流。

接触网上方有平行接近的高压交流输电线路时，在接触网通过的路径上，输电线路在该路径的各点上所产生的空间电位大小和相位相同。而接触网上方交叉跨越高压交流输电线路时，输电线路在接触网通过的路径各点上所产生的空间电位大小和相位逐点不同[8]，此时计算感应电压和电流较平行接近的情况复杂。

计算接触网上方平行接近高压交流输电线路时的感应电压和电流时，可以运用已有的多导体传输线模型进行计算，但为了计算接触网上方垂直交叉跨越高压交流输电线路时的感应电压和电流，需要将接触网分成n个小段，当分段足够多时，即可近似看作每小段与高压交流输电线路呈平行接近状态，计算得到每小段的感应电压和感应电流，并进行叠加计算，最后可得到接触网总的感应电压和电流。计算接触网T线上方斜交叉跨越高压交流输电线路A、B、C三相时的感应电压和电流，如图1所示，先按其长度L和交叉角α求出相应长度L·sinα的垂直交叉段的感应电压，该电压即为长度为L的斜交叉感应电压，进而求得感应电流。

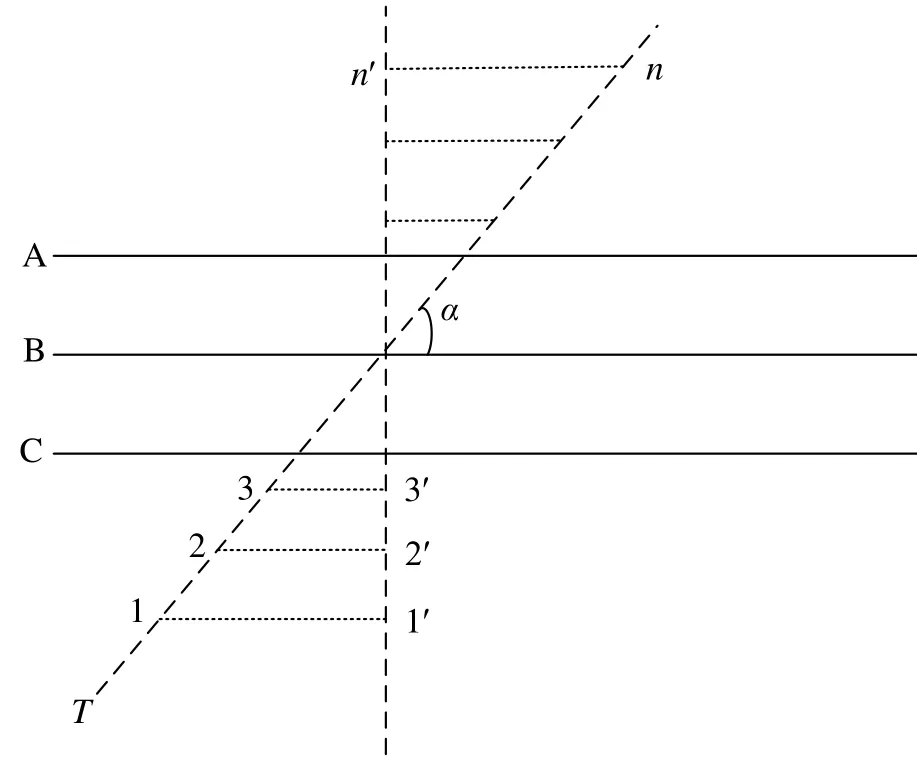
图1 接触网上方交叉跨越高压交流输电线路分段示意

为了简化计算，忽略交叉区域附近高压交流输电导线对地距离的变化，并将线路按无限长考虑，同时不考虑接触网对高压交流输电线路上电荷分布的影响。下文只针对一回高压交流输电线路对接触网耦合情况进行计算，若存在多回高压交流输电线路平行接近或交叉跨越接触网，可以分别计算各回高压交流输电线路在接触网上产生的感应电压和电流，最后进行叠加处理。高速铁路接触网与高压交流输电线路的耦合原理如图2所示，其中A、B、C表示高压交流输电线路三相，T、F、R表示接触线、负馈线、钢轨，C、Z各下标表示导体自电容、互电容以及自阻抗、互阻抗。

图2 高速铁路接触网与高压交流输电线路耦合原理

2 多导体传输线模型感应电计算

利用已有的多导体传输线模型和上文所述的分段算法可以全面准确地对接触网上方平行接近或交叉跨越高压交流输电线路时的感应电进行计算。下文针对容性感应电压、感性感应电压、容性感应电流、感性感应电流分别进行分析。

2.1 容性感应电压

设交流多导体系统由n根参数均匀分布的平行架设导体组成，以大地为参考，任一导体的电压为，i=1,2,…n，通过单位长度导体的电流为，若略去线路对地电导，已知系统电容矩阵C，则可列写多导体系统在正弦稳态的条件下电流降与电容、电压的稳态微分方程：

式中：w= 2πf，f为多导体系统正弦电压频率。

令

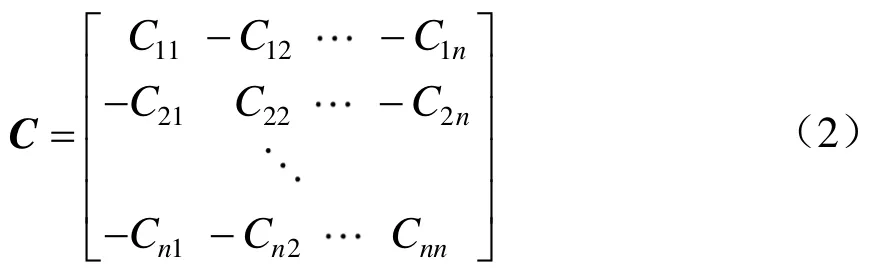
其中，C为Maxwell电容矩阵，对角线元素是导体对地单位电容和该导体与其他导体单位互电容之和，即

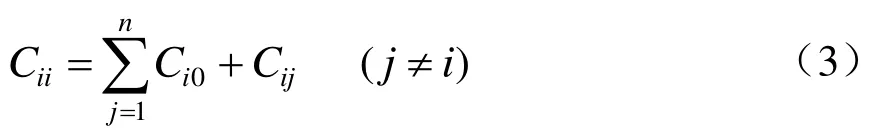
式中：Ci0为导体对地单位电容；Cij为导体之间的单位互电容。

非对角线元素为导体间单位互电容，有

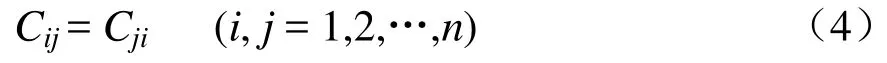
在多导体系统中，假设由于某种原因，导体n停运而两端开路，即，其他导体正常运行，将式（1）第n行展开，可得导体n的容性感应电压[9]：

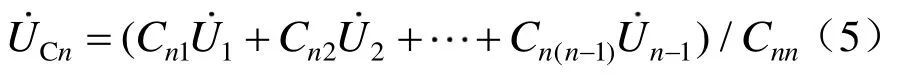
从式（5）可以看出，停运导体上耦合的容性感应电压是多导体系统电压和分布电容的函数，与停运导体的长度无关。特殊情况下，当导体n存在某一端接地时，接地处对地电容被短路，接地线屏蔽了系统中其他带电导体对导体n的电容耦合作用，致使接地处电容感应电压为零，其他位置电容感应电压大幅降低。

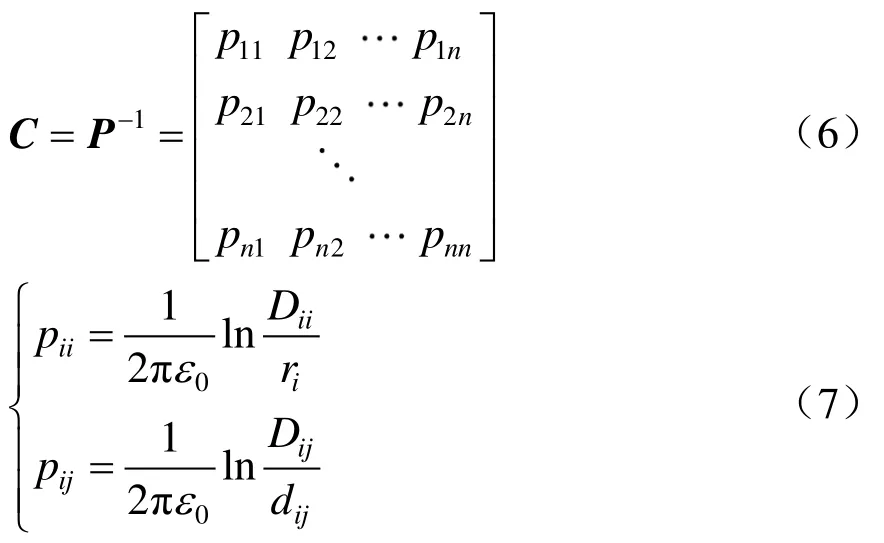
式中：Dii为导线i与其镜像之间的距离；Dij为导线i与导线j的镜像之间的距离；ri为导线i的半径；dij为导线i与导线j之间的距离；ε0为空气介电常数。

在接触网停电检修不挂接地封线时，线路上的感应电压主要是高压输电线路通过线间电容和对地电容在接触网上耦合的容性感应电压。在接触网与高压输电线路交叉跨域区段，以每一小段接触网线路的中点作为该小段的坐标位置，得到接触网各小段的电压，计算得到各小段容性感应电压为

式中：CT为接触网单位自电容；CTA、CTB、CTC分别为高压输电线路三相导线与接触网 T线的单位互电容；CTR、CTF分别为接触网与等值 R线和同侧F线的单位互电容；UA、UB、UC分别为高压输电线路三相导线电压；UR、UF分别为等值R线和同侧F线电压。

对容性感应电压进行近似计算时，考虑到正馈线和等值 R线电压较小，可忽略其容性影响，因此式（8）可进一步简化为

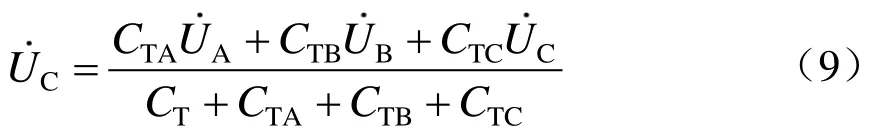
令Cs1为接触网导线对地单位电容和该导体与三相输电线路互电容之和，即

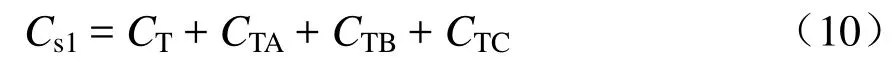
则式（9）可表示为

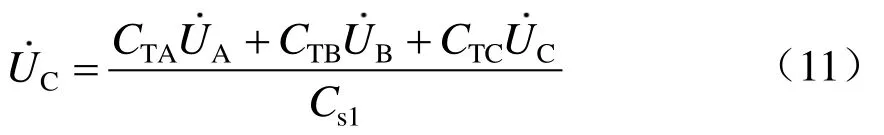
将每一小段的感应电压实部与虚部分别叠加，即可得到停电接触网的总容性感应电压为

根据脑梗死患者病情差异,采用不同的治疗方法,如针对风痰阻络证患者,可以给予患者使用三七、银杏叶制剂;对于气血血瘀症的患者,可以给予患者注射参麦注射液;对于阴虚风动证的患者,可以给予患者使用脉络宁。并且,在患者平常的治疗中,可以指导患者使用金银花泡水漱口、使用生姜水擦拭身体,这样主要是起到清热解毒及祛风散寒的效果。

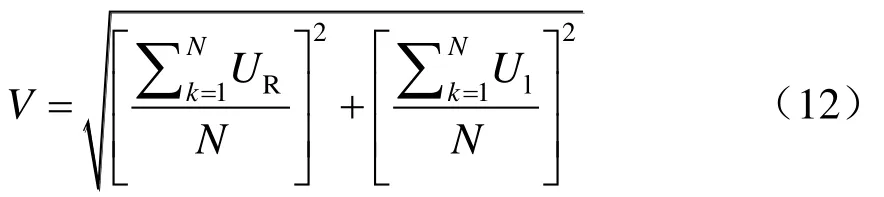
式中：N为计算接触网与高压输电线路交叉跨域区段时的分段数；UR，Ul分别为每一小段的感应电压实部与虚部。

若存在多回高压输电线路平行或交叉跨越接触网的情况，可以分别计算各回高压输电线路在接触网上产生的感应电压和感应电流，最后进行叠加处理，可得到停电接触网的总容性感应电压。

2.2 感性感应电压

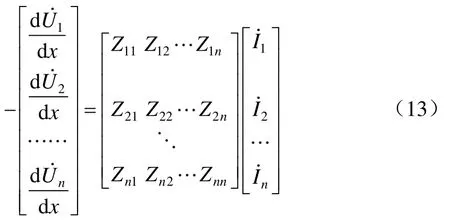
导体n停运而两端断开时，即时，将式（13）第n行展开可得

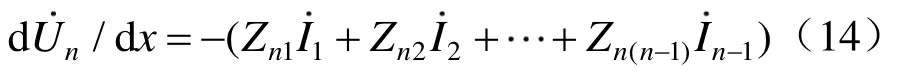
若规定停运导体上感性感应电势方向为末端（x=l处）指向首端（x= 0处），假设各导体均匀分布，则第n根长度为l导体上感性感应电势为

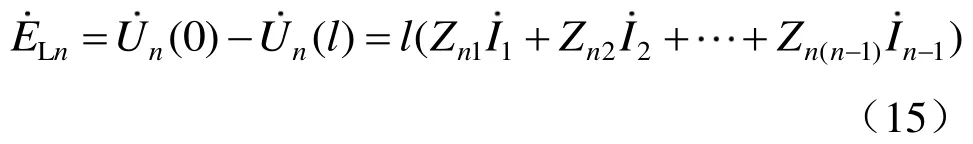
从式（15）可以得出，感性感应电势为关于停运导体长度、多导体系统电流和阻抗的函数，距离停运导体首端越远，感性感应电势越大。特殊情况下，当导体n有一端接地时，接地端容性感应电压为零，不接地端由于电磁耦合作用仍会产生感性感应电压。

假设停运导体n首端对地绝缘，末端接地，即式（14）满足边界条件，，可以得出首端感应电压为

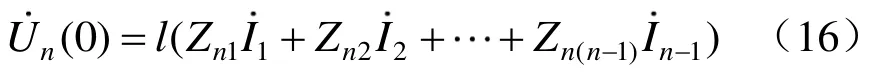
反之，当停运导体n首端接地，末端对地绝缘，即式（14）满足边界条件，，可以得出末端感应电压为

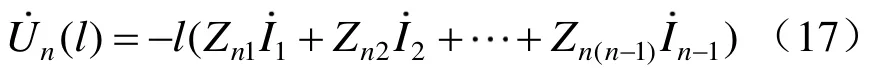
当停运导体n两端均对地绝缘，式（14）满足边界条件，可得首末端感应电压分别为

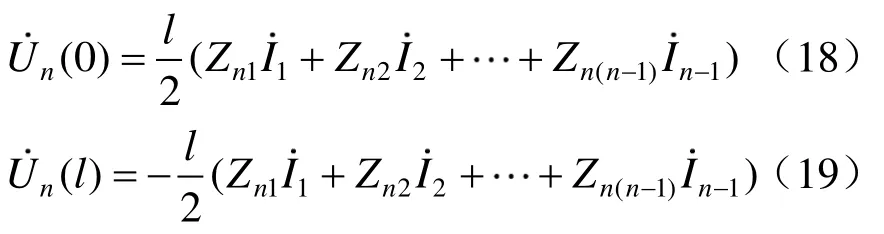
在接触网停电检修时，高压输电线路上通过的负荷电流通过线间互感在接触网上耦合出感性感应电压。利用 Carson公式，求得高压输电线路中导线或接触网导线自阻抗为

式中：R为导线单位长度有效电阻；Dg为导线—地回路等值深度，取决于大地电导率σ及电流的频率f；re为导线的有效半径。

接触网导线与高压输电线路间的互阻抗为

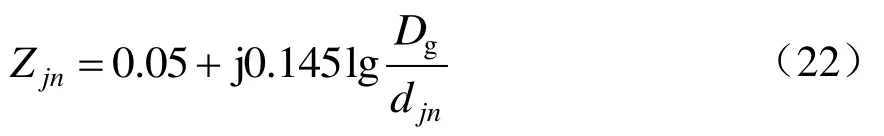
式中：djn为接触网导线j与高压输电线路n的距离。

高压输电线路正常运行时，三相电流平衡，有

式中：α= ej120°，并且满足 1 +α+α2= 0；IA、IB、IC为各相电流幅值。

当停电接触网两侧接地时，线路上感应电压主要由电磁耦合作用产生，求得每回高压输电线路各相在接触网每小段导线上产生的感性感应电压Ek：

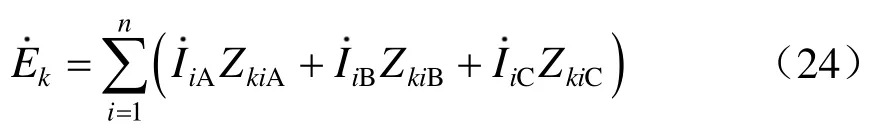
式中：IiA，IiB，IiC为第i回高压输电线路三相导线电流；ZkiA，ZkiB，ZkiC分别为接触网导线第k小段与第i回高压输电线路A、B、C三相的互阻抗。

若不计接触网导线与高压输电线路间互电阻，将式（22）、式（23）代入式（24）进一步化简得

式中：IiA为第i回高压输电线路A相导线电流；dkiA，dkiB，dkiC分别为接触网导线第k小段与第i回高压输电线路A、B、C三相的垂直距离。

进而可得到停运线路总感性感应电压。

2.3 容性感应电流

通过停运导体n的感应电流与该导体的接地方式有关。当停运导体n两端不接地时，导体n上流过的感应电流为零。当导体n有一端接地时，接地处的感应电压通过对地电容形成通路而流过容性感应电流，而感性感应电流无通路，因此接地处电流近似为容性感应电流In(容)：

式中：w= 2πf，f为高压交流输电线路频率；Cnn为导体n对地单位电容和该导体与其他导体单位互电容之和；Vn为停运线路感应电压。

当停电接触网有一端经接地封线接地时，接地处的感应电压通过对地电容形成通路而流过容性感应电流：

式中：Cs1为接触网导线对地单位电容和该导体与其他各导体单位互电容之和；l1为接触网导线与高压输电线路的并行长度；为容性感应电压。

2.4 感性感应电流

导体n两端均接地时，对地电容被短接，线路容性电流为零，而感性感应电压在导体上形成通路，因此导体n上近似感性感应电流In(感)为

式中：Vn为停运导体感应电压；Znn为导体n的自阻抗；Z为接地电阻阻抗。

若接触网导线检修时两端均经接地封线接地，则在电磁感应电动势的作用下会在接触网导线与大地间产生环流，即接地处会流过感性感应电流：

式中：E为电磁感应电动势；ZT为接触网导线单位长度自阻抗；d为两接地点间距；Zd为两接地封线与大地间等效阻抗。

3 感应电影响因素分析

3.1 输送功率影响

在计算模型中接触网对地高度6.3 m，高压输电线路选取110 kV单回输电线路，三相导线水平完全换位布置，线间距离为2 m，与停电接触网的交跨距离为15 m，交跨角度为90°，110 kV高压输电线路的输送功率分别取20，30，40，50 MW，功率因数为 0.8（滞后），计算停电接触网不接地、首端变电所单端接地时的感应电压、首端变电所单端接地以及末端分区所同时接地时流过接地线的感应电流，计算结果见表1。

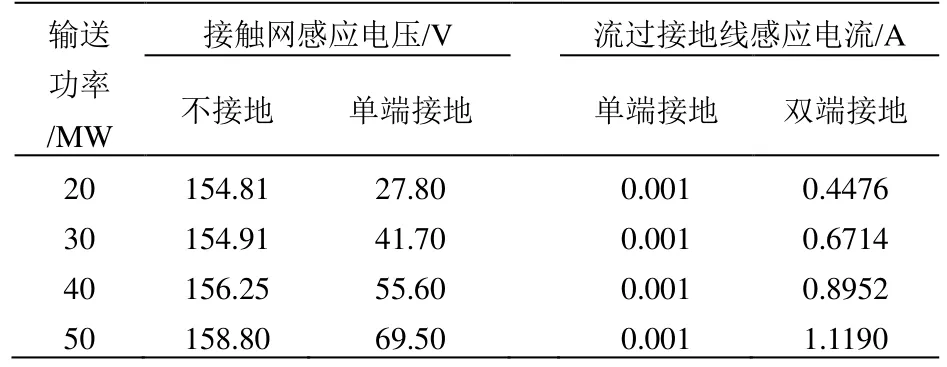
表1 高压输电线路不同输送功率下接触网感应电压电流

从表1可以看出：高压输电线路输送功率增大时，停电接触网（不接地时）上感应电压变化很小，这是因为停电接触网主要受到高压输电线路的容性耦合作用；当首端变电所单端接地时，停电接触网的对地分布电容被短路，高压输电线路与停电接触网的容性耦合作用被大幅削弱，只存在感性感应电压，在接地线处流过较小的容性感应电流；单端接地时的感性感应电压和双端接地时流过接地线的感性感应电流与高压输电线路输送功率成正比。

3.2 交跨距离影响

保持110 kV单回输电线路输送功率30 MW，交跨角度为90°不变，改变高压输电线路与停电接触网的交跨距离，计算停电接触网在不同工况下的感应电压和电流，计算结果见表2。

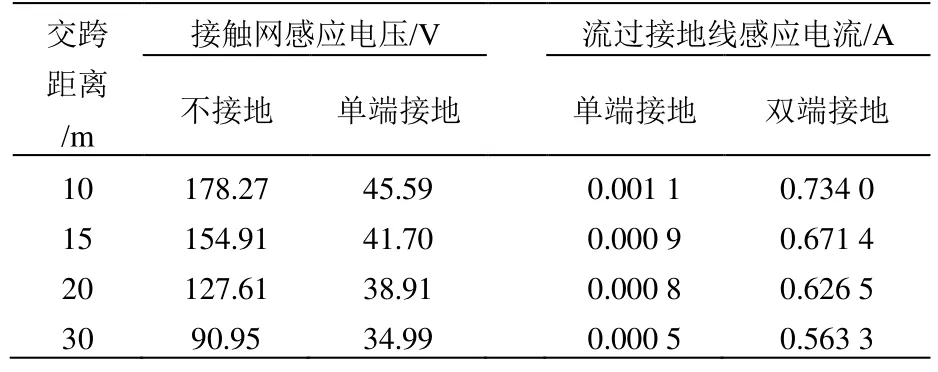
表2 不同交跨距离下接触网感应电压电流

从表2可以看出：高压输电线路与停电接触网的交跨距离越大，停电接触网上的感应电压和电流越小，这是因为随着高压输电线路与停电接触网的交跨距离增大，两者的互感和互电容减小，电磁耦合和静电耦合减弱，表现出感应电压和电流均减小；高压输电线路与停电接触网的交跨距离从10 m增至30 m时，停电接触网上不接地时的感应电压从178.27 V降至90.95 V，可见交跨距离对停电接触网不接地时的感应电压影响较为显著。因此，实际工程中可以通过增大外部电网与接触网的交跨距离来减小外部电网在接触网上的感应电压。

3.3 交跨角度影响

保持110 kV单回输电线路输送功率30 MW，与停电接触网的交跨距离15 m不变，改变高压输电线路与停电接触网的交跨角度，计算停电接触网在不同工况下的感应电压和电流，计算结果见表3。

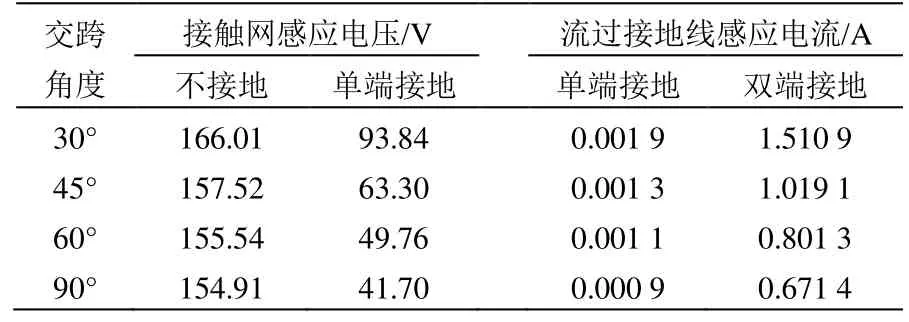
表3 不同交跨角度下接触网感应电压电流

从表3可以看出：高压输电线路与停电接触网的交跨角度越大，停电接触网上的感应电压和电流越小。这是因为当交跨角度增大时，高压输电线路与停电接触网之间并行长度减小，而停电接触网上感性感应电压、感性感应电流与容性感应电流均与高压输电线路与停电接触网之间并行长度成正比，表现出感应电压和感应电流均减小。

4 结论

本文首先分析了停电检修接触网上方交叉跨越高压交流输电线路时的感应电耦合原理，提出了利用多导体传输线模型计算停电检修接触网感应电，考虑到高压交流输电线路在接触网通过的路径各点上所产生的空间电位大小和相位的差异，将接触网进行分段处理，计算每一小段的感应电压和电流，叠加得到接触网上总感应电压和电流，最后利用 Matlab编程计算了接触网在高压交流输电线路不同输送功率、交跨距离、交跨角度下的感应电大小，分析计算结果得出以下结论：

（1）停电检修接触网主要受到高压交流输电线路的容性耦合作用，线路输送功率增大时，停电接触网上感应电压变化很小；当接触网在首端变电所及末端分区所接地时，高压输电线路与停电接触网的容性耦合作用被大幅削弱，感应电压较小，在接地线处流过较小的容性感应电流；单端接地时的感性感应电压和双端接地时流过接地线的感性感应电流与高压输电线路输送功率成正比。

（2）高压交流输电线路与停电检修接触网交跨距离越大，停电接触网上的感应电压和电流越小；交跨距离对停电接触网上不接地时的感应电压影响较为显著，实际工程中可以通过增大高压输电线路与接触网的交跨距离来减小高压输电线路在接触网上的感应电压。

（3）高压交流输电线路与停电检修接触网交跨角度越大，停电接触网上的感应电压和电流越小。