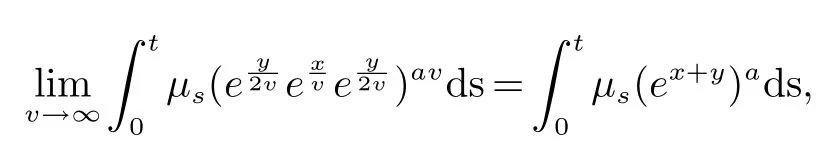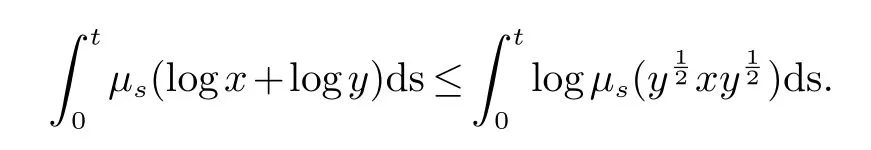有关算子的一些Log-次优化不等式和对称拟范数不等式∗
王云,闫成
(新疆大学 数学与系统科学学院,新疆 乌鲁木齐 830046)
0 引言
设Mn是由全体n×n 复矩阵构成的矩阵代数.称Mn上的范数‖|·|‖为酉不变范数,如果对任意A ∈Mn和酉矩阵U,V ∈Mn,有‖|UAV|‖=‖|A|‖.记为Mn的正部.对于任意A ∈Mn,我们用λ1(A),···,λn(A)表示A 的特征值,定义A 的奇异值为的特征值按降序排列并按重数计算形成的数列,记为µ1(A),···,µn(A).
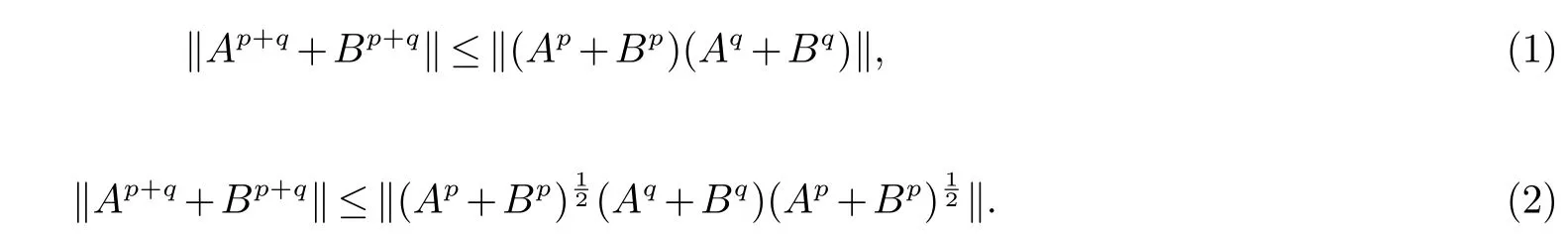
为了解决Bourin 的问题,Hayajneh-Kittaneh 在[2]中提出了如下更强的猜想:

事实上,分别用Ap,Aq,Bp和Bq代替A1,A2,B1和B2,我们可以得到不等式(1),(2).
若Ai,Bi∈使得AiBi=BiAi.最近Lin 在[3]中证明了

这个不等式解决并推广了Hayajneh-Kittaneh 的猜想(3).另一方面,若Ai,Bi∈使得AiBi=BiAi.Liu等在[4]中证明了下述不等式

这个不等式解决并推广了Hayajneh-Kittaneh 的猜想(4).
2016年,Han等在[5]中证明了与半有限von Neumann 代数有关的非交换Lp空间上的p-范数不等式(5).本文的目的是证明一些log-次优化和一些有关非交换对称拟Banach 空间中的拟范数的不等式.采用文献[6−8]中的方法,我们得到了一些log-次优化不等式.作为应用,我们证明了不等式(5)和(6)在具有序连续拟范数的非交换对称拟Banach 空间是成立的.
1 准备知识
我们用M 表示一个可分的Hilbert 空间H 上的具有正规半有限忠实的迹τ 的半有限von Neumann 代数,用M+表示它的正部.令S+(M)={x ∈M+:τ(s(x)<∞)}且S(M)是S+(M)的线性组合.S(M)中的元称为τ 有限支撑的.为了叙述方便,通常把S+(M)和S(M) 分别简记为S+和S.称H 上的一个闭稠定算子重属于M 如果对M 的交换子M′中的任一酉元u 有ux=xu.重属于M 的算子x 称为关于τ 可测的(或称为可测的),如果对任意δ>0 都存在e ∈P 使得

记L0(M)为可测算子全体构成的拓扑空间.
定义1设x ∈L0(M,τ)且t>0.定义x 的广义奇异值µt(x)为

在不产生混淆的情况下,我们也用µ(x)表示函数t →µt(x).若x 是正可测算子,则

关于µt(x)的基本性质,请参见文献[7].
对于x ∈L0(M),t>0.我们定义

为了确保Λt(x)的定义有意义(即∞−∞不会出现),在本文的剩余部分,我们将只考虑满足下述条件的可测算子:x ∈M 或µt(x)≤Ct−α,C,α>0.
设x,y 是τ−可测算子.我们有

更多相关知识请参见文献[7,9].
拟Banach 函数空间E 称为对称拟Banach 空间,如果对于f ∈E,g ∈L0(0,∞),µ(g)≤µ(f),我们有g ∈E和‖g‖E≤‖f‖E(更多的相关知识见文献[6,10]).
对于0 设E 是(0,∞)上的对称拟Banach 空间.我们说E 是有序连续拟范数‖·‖,如果对E 中任意的fi,i ∈I 满足fi↓0 的网,有‖fi‖↓0.定义 则(E(M),‖·‖E(M)) 是非交换对称拟Banach 空间.若E=Lp,则(E(M),‖·‖E(M))是非交换Lp空间(Lp(M),‖·‖p).对于0 若E 是对称拟Banach 空间,则E(r)(M)=E(M)(r),其中 设α>0,拟Banach 空间E 称为α-凸的,如果存在常数C>0 使得对所有的有限序列xn∈E 有 更多相关知识参见文献[6,10]. 定义2设x,y ∈M.我们说x log-次优化于y 记为x ≺logy 当且仅当 为了证明主要结论我们需要下面的两个引理.下述引理分别由文献[11]中的定理5.11 和文献[12]中的注1得到. 下面的推论可以由引理3 直接得到,为了阅读方便我们给出了具体的证明. 证明应用引理1,文献[13]中的引理3.4 和文献[12]中的定理2,我们可以得到 证明应用文献[14]中的定理(或[15])可以得到xy ∈E(r)(M).由E(M)是一个α-凸对称拟Banach 空间可知,E(r)是rα-凸的.则 其中:V 是(0,∞)上的一组正测度.(参考文献[16]中的550 页)计算可得 现在我们来证明本文的主要结论. 证明由文献[14]中的定理3 可知 取0 ≤xi∈E(M)(p)∩M,0 ≤yi∈E(M)(q)∩M,i=1,2,···,k,则 因此A 是PPT.故 也是PPT.应用推论2 可得 所以,应用文献[7]中的引理2.6 可得 故 另一方面,由文献[7]中271 页可知τ(e(n,∞)(x))→0,n →∞.由此可知 进而 类似可得, 由文献[14]中的定理3 可得 类似可得 n →∞.进而 n →∞.因此 n →∞.结合(14),(15) 和(16) 可知 引理4设E 是对称Banach 空间.若0 ≤xi,i=1,2,···,k ∈E(M),则 证明令f(t)=tr,r ≥1.应用文献[19]中的定理5.3 可知 因此,此引理可以由(17)和(13)直接得到. 证明首先,由文献[14]的定理3 可知 在定理1 中取x1=xt,y1=x1−t,x2=yt,y2=y1−t,n=2,有下述不等式. 推论4设x,y ∈E(M)+.则 在这一节,我们将给出一些log-次优化不等式.设f 是[0,∞)上的非负实函数.函数f 被称为log-凸的,如果 其中:0<α<1,s,t ∈[0,∞). 命题2设f 是[0,+∞]上满足f(0)=0 的连续增函数且t →f(et)是凸的.若x,y ∈L+0(M),p ≥q>0,则 特别地,若x,y ∈M,则 在上述不等式取f(t)=ta,a>0,可以得到 下述引理证明与矩阵的方法相似. 引理5设x,y ∈M 是自伴算子.则 定理2 设x,y ∈M 是自伴算子.则 应用文献[7]中的引理2.5(i)(v)可得µt+s(T)≤µs(T−S)+µt(S)和µt+s(S)≤µs(S−T)+µt(T).因此对于0 由(20)和引理5 可推断出 故, 取a ↓0 可知结论成立(见文献[7]中288 页). 推论5若x,y ∈M+是可逆的,则 证明应用定理2,我们推出 再应用文献[7]中的引理2.5(v)即可得到我们需要的结论. 引理6设f 是(0,∞)上的一个凸连续非负递增函数且x,y ∈M+.则 证明若x ≥0,则f(〈xξ,ξ〉)≤〈f(x)ξ,ξ〉,其中ξ ∈H. 因为x,y ∈M+,由(7)可得 因此, 定理3设logf 是(0,∞)上的一个凸连续非负递增函数.若x,y ∈M+是可逆的,则 证明结合引理2,推论5 和引理6 可得

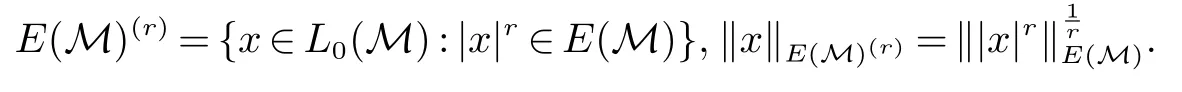



2 主要结论


















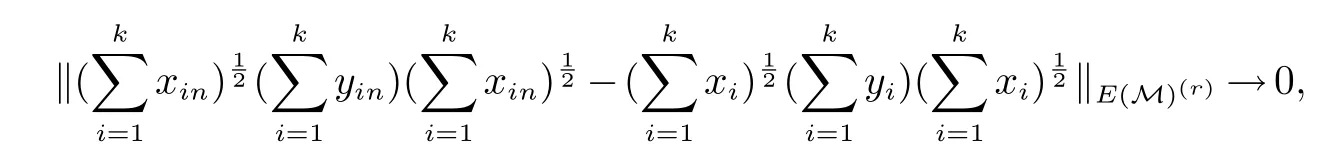

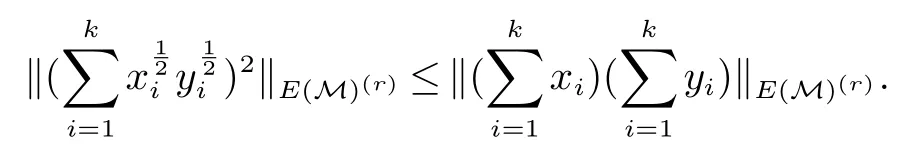






3 Log-次优化不等式