关于Heinz均值的Log-次优化不等式∗
蒋雪瑶,韩亚洲
(新疆大学 数学与系统科学学院,新疆 乌鲁木齐 830046)
0 引言
本文中我们用Mn表示由n×n 阶复矩阵构成的集合.称Mn上的范数‖|·|‖为酉不变范数,若对任意的A ∈Mn和酉矩阵U,V ∈Mn,有‖|UAV|‖=‖|A|‖.设A ∈Mn且{sj(A)}为A 的奇异值,定义A 的Ky Fan k-范数(k=1,2,···,n)为
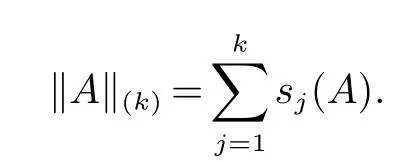
设A,B ∈Mn,应用Fan Dominance定理(见文献[1]中定理IV.2.2)可知‖|A‖|≤‖|B‖|的充分必要条件是‖A‖(k)≤‖B‖(k),k=1,2,···,n.由此可知Heinz 均值不等式(见文献[1]中265页)有如下变形

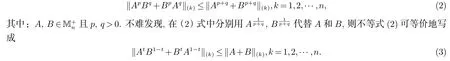
此后这个不等式引起了很多学者的关注.2013 年,Hayajneh-Kittaneh 在[3]中证明了当p=1,2,3 且q=1 时不等式(2)对于Hilbert-Schmidt 范数成立.随后,Bhattia 在文献[4]中又证明了当时不等式(3)对于Hilbert-Schmidt 范数成立.最近,Hayajneh等在[5]中研究算术-几何平均不等式的过程中,得到了一个比不等式(3)稍弱的不等式
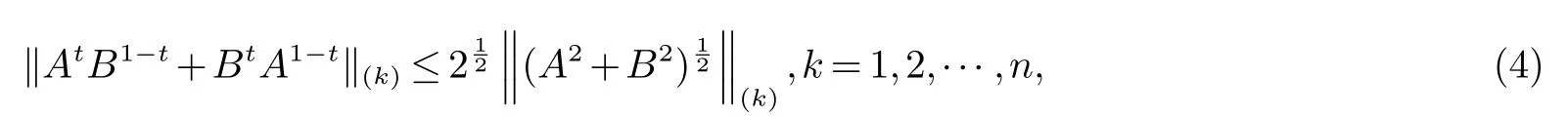
本文的目的是利用文献[5,10,11]中的方法把次优化不等式(4)推广到log-次优化不等式的情形.更确切地说,我们要证明如下结论:设0 ≤x,y ∈M 且f 和g 是算子凹函数,则
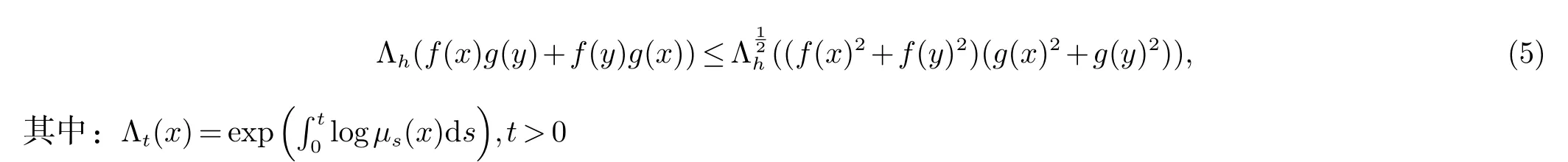
在这个过程中我们得到了
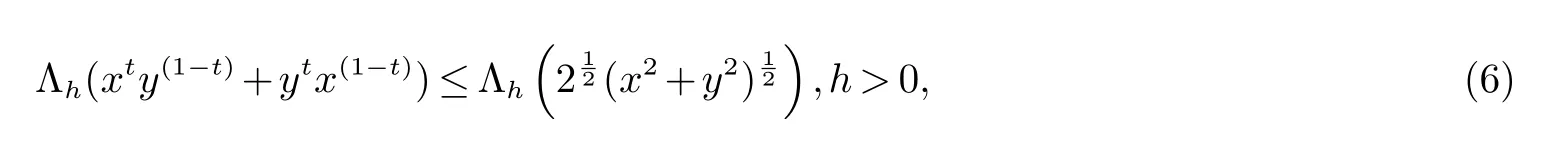
这里0 ≤x,y ∈M 且0 ≤t ≤1.这个不等式特殊形式正是不等式(4).此外,我们还得到了另外一个有意思的不等式
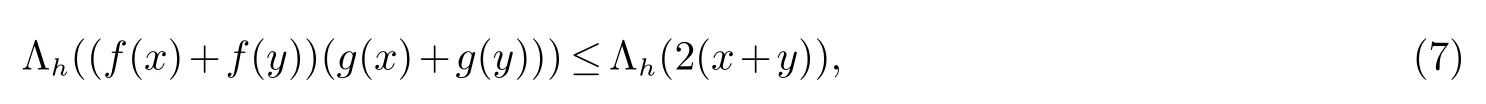
这里0 ≤x,y ∈M 且f,g 是两个算子凹函数,且f(x)g(x)=x.
1 准备知识
设M ⊆B(H)是可分Hilbert 空间H 上的一个冯·诺依曼代数.记M+={x ∈M:x ≥0}.我们称定义在M+上的线性函数τ:M+→[0,∞] 为M 上的迹,若τ 是可加的,正齐次且酉不变的.称迹τ:M+→[0,∞]是
(1)忠实的,如果x ∈M+且τ(x)=0,则x=0,
(2)半有限的,如果x ∈M+且τ(x)>0,则存在0 ≤y ≤x 使得0<τ(y)<∞,
(3) 正规的,如果xi↑ix在M+中,则0 ≤τ(xi)↑iτ(x).
在本文中我们将沿用上述记号,且在没有特别说明的情况下M 始终表示定义在一个可分Hilbert 空间H上的一个具有正规的忠实的半有限迹τ 的半有限冯·诺依曼代数.更多的有关冯·诺依曼代数的基础知识见文献[12].
定义1设x ∈M,t>0.我们定义广义奇异值µt(x)为
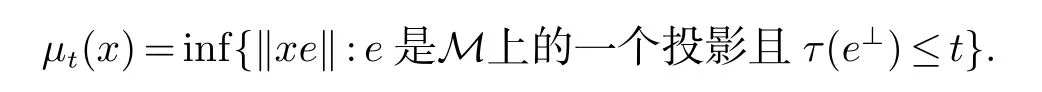
为了叙述方便,在不引起混淆的情况下分别用λ(x)和µ(x)表示函数t →λt(x)和t →µt(x).
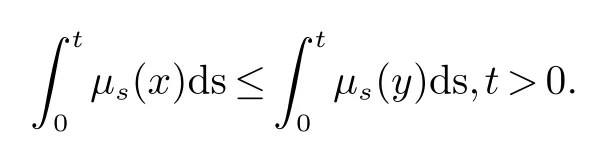
若x ∈M,则下面的定义是合理的(见文献[10])
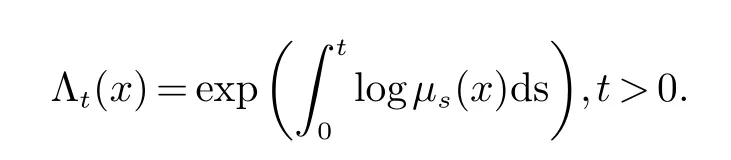
设x,y ∈M,则称x ≺logy(x log-次优化于y),若
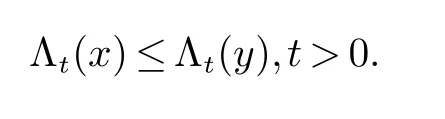
更多的有关µ(x)和Λ(x)的基本知识参见[10,13].
2 主要结论
设f 为定义在[0,∞)上的非负函数.称正函数f 为[0,∞)上的算子凹函数,若对所有的x,y ∈M+,有

为了得到我们的主要结论,我们需要下面几个简单的引理.
引理1 设x,y ∈M,x 和y 是自伴算子.则

证明引理1的不等式是下述不等式的简单推论
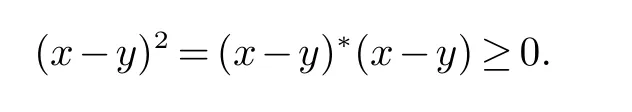
由于f(x)=xt(0 ≤t ≤1)是[0,∞)上的算子凹函数,因此引理2成立.
引理2设0 ≤x,y ∈M 且0 ≤t ≤1.则

引理3设0 ≤x,y ∈M 且0 由此可知结论成立. 定理1设0 ≤x,y ∈M.如果f 和g 是[0,∞)上的算子凹函数,则 证明设 应用文献[10]中的引理2.5 和引理3 可以得到 推论1设0 ≤x,y ∈M 且0 ≤t ≤1.则 (1) Λh(xtyt+ytxt)≤Λh(21−t(x2+y2)t),h>0. (2) 若x,y ≥0,则µt(xy)=µt((xy)∗)=µt(y∗x∗)=µt(yx).再结合Λ(x)和µ(x)的定义和性质可以得出 因此,应用引理2可得 推论2设0 ≤x,y ∈M 且0 ≤t ≤1.则 证明因为f(t)=ept,p>0 是一个凸函数,所以利用推论1 和文献[15]的定理2 即可得到我们想要的结论. 在这一节中,我们将考虑与(4)相关的另一种形式的log-次优化不等式. 定理2设0 ≤x,y ∈M.如果f 和g 是两个定义在[0,∞)上的算子凹函数且f(x)g(x)=x,则 证明根据算子凹函数的性质,有 因此存在收缩算子u,v ∈M 使得 利用[10]中的引理2.5 可得 推论3设0 ≤x,y ∈M且0 ≤t ≤1.则 证明结合引理2,引理3,等式(8)和文献[10]中的定理4.2 可得 命题1设0 ≤x,y ∈M 且0 ≤t ≤1.则 证明由引理1,引理2,等式(8)和文献[10]中的定理2.5 可知




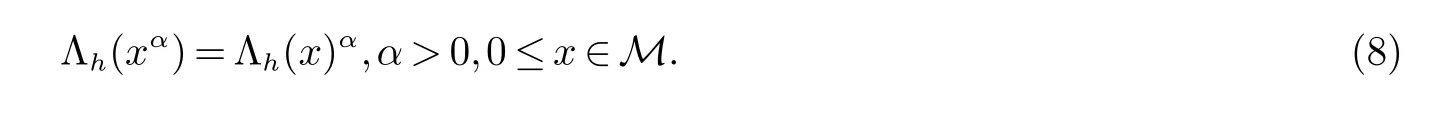
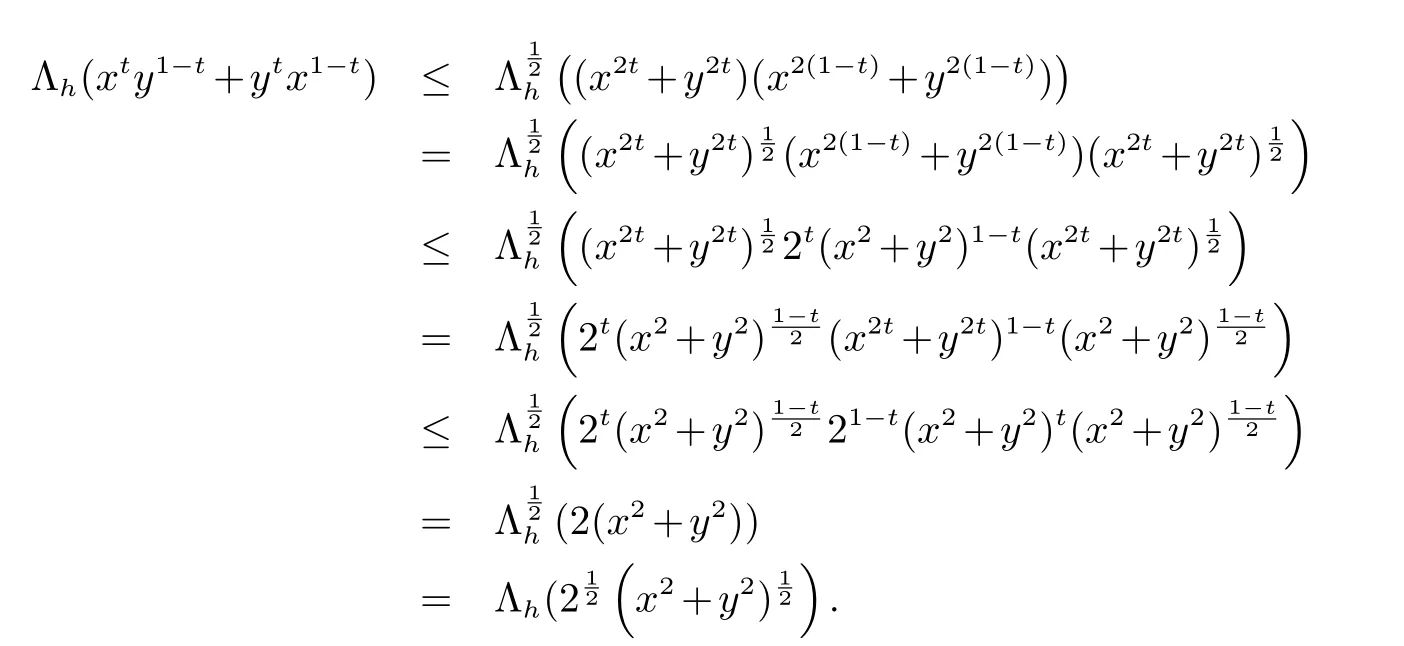
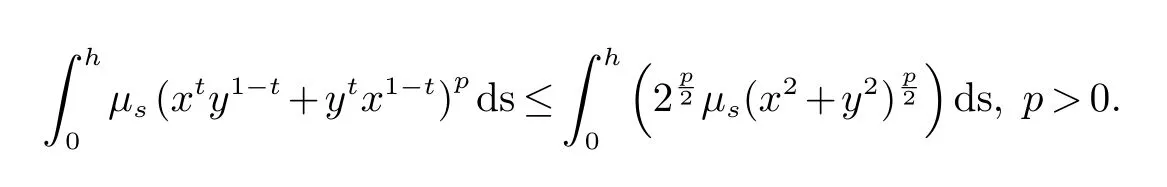
3 与Log-次优化相关的不等式
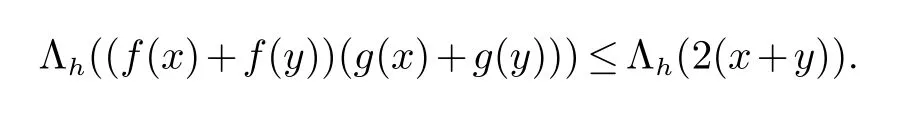
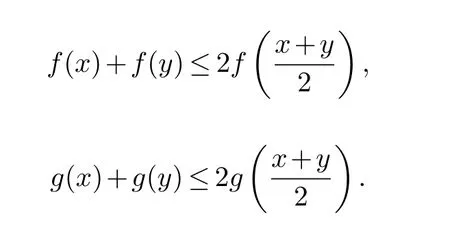
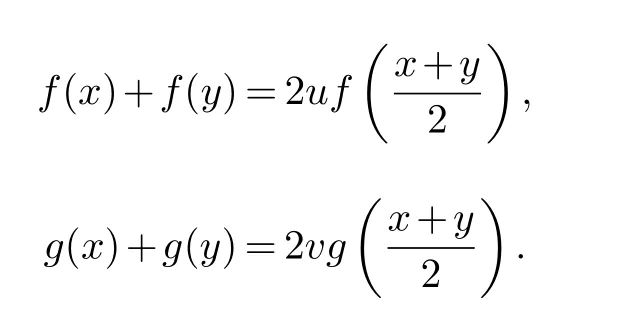
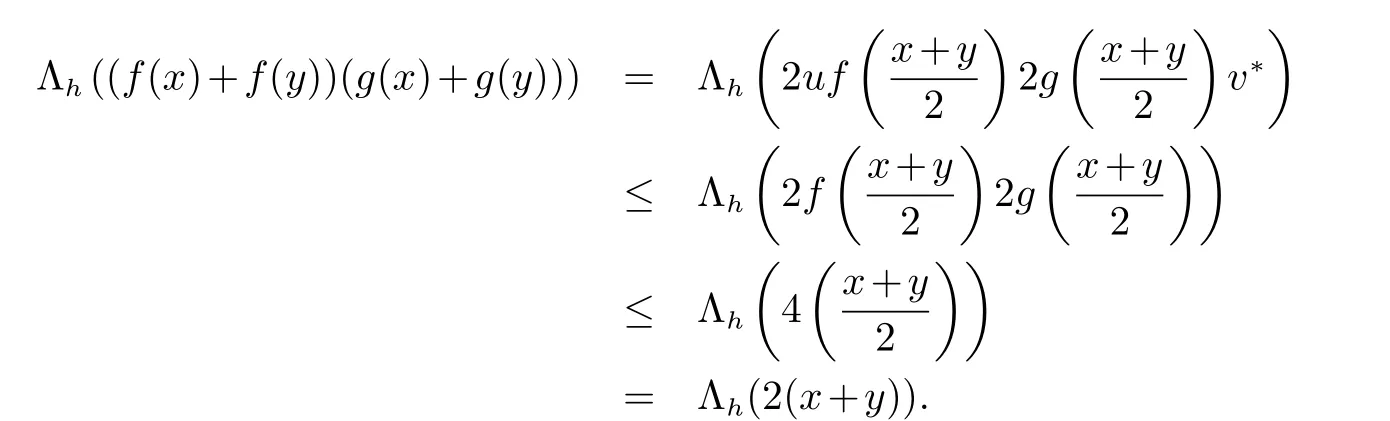


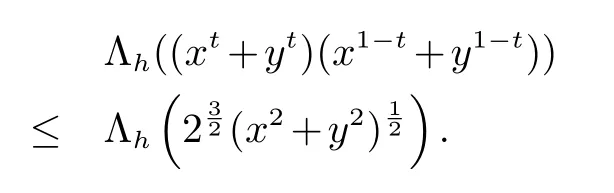
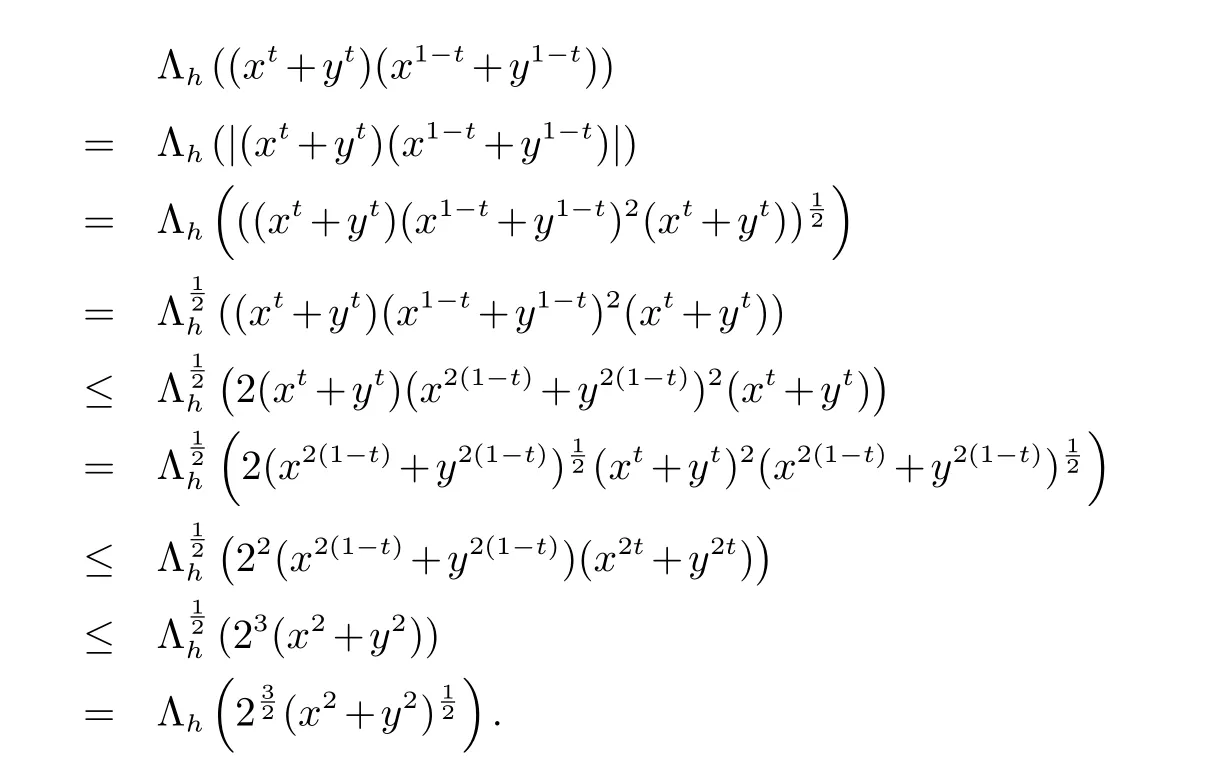
- 新疆大学学报(自然科学版)(中英文)的其它文章
- On Size,Order,Minimum Degree and Conditional Diameter of Graphs∗
- 给定点数,最小度和条件直径的图的边数的上界∗
- Some Logarithmic Submajorisation Inequalities Related to Heinz Mean∗
- Logarithmic Submajorization and Symmetric Quasi-Norm Inequalities on Operators∗
- 有关算子的一些Log-次优化不等式和对称拟范数不等式∗
- 新疆伊犁青少年短跑成绩影响因素研究∗

