On Size,Order,Minimum Degree and Conditional Diameter of Graphs∗

MA Huaping,TIAN Yingzhi

(School of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)

Abstract:The diameter D(G) of a graph G is the the maximum distance between two vertices in G.For given positive integers l and s,the conditional diameter D(G;l,s)of a graph G is the maximum distance between two subsets of vertices with cardinalities l and s.When l=s=1,the conditional diameter D(G;1,1)is just the diameter D(G)of G.In this paper,we obtain an asymptotically tight upper bound on the size of G in terms of order,minimum degree and conditional diameter.

Key words:diameter;conditional diameter;minimum degree

0 Introduction

For graph-theoretical terminologies and notation not defined here,we follow[1].In this paper,we consider finite simple graphs.LetGbe a graph with vertex setV(G)and edge setE(G).Theorder n=|V(G)|ofGis the number of its vertices,while thesize m=|E(G)|ofGis the number of its edges.For each vertexv∈V(G),theneighborhood NG(v)ofvis defined as the set of all vertices adjacent tov,anddG(v)=|NG(v)|is thedegreeofv.Theminimum degreeofGis denoted by δ(G).For two disjoint subsets of verticesV1andV2,[V1,V2]Gis the set of all edges inGjoining a vertex inV1and a vertex inV2.Thefloorof a real numberx,denoted byx,is the greatest integer not larger thanx;theceilingof a real numberx,denoted byx,is the least integer greater than or equal tox.

Thedistance dG(u,v)between two verticesuandvis the length of a shortest path fromutovinG.Thediameter D(G)ofGis max{dG(u,v):u,v∈V(G)}ifGis connected;otherwiseD(G)=∞.IfV1⊆V(G)andV2⊆V(G)are two nonempty sets of vertices,the distance betweenV1andV2,denoted bydG(V1,V2),is the minimum distancesdG(u,v)withu∈V1,v∈V1.If there is no ambiguity,we always delete subscriptGinNG(v),dG(v),[V1,V2]G,dG(u,v)anddG(V1,V2).

As a generalization of diameter,Balbuena et al.[2] introduced conditional diameter of a graphG.Given a property P satisfied by at least one pair (V1,V2) of nonempty subsets ofV(G),theconditional diameter DP(G) is defined as max{dG(V1,V2):∅≠V1,V2⊆V(G),where(V1,V2)satisfies property P}.Because conditional diameters measure the maximum distance between subsets of vertices with given property,they could be used in some applications where the communication delays between particular network clusters need to be controlled.

Letlandsbe two integers with 1 ≤s≤l.Consider the property P as follows:(Vl,Vs)⊆V(G)×V(G)satisfies P if and only if|Vl|=land|Vs|=s.In this case,the conditional diameterDP(G)is denoted byD(G;l,s)in[3],which is defined as

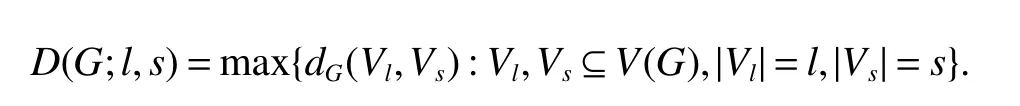
Note thatD(G;1,1) is exact the diameterD(G),andD(G;l,s)=0 if and only ifl+s>|V(G)|.Moreover,D(G;l,s) ≤|V(G)|+1−(l+s)whenl+s≤|V(G)|.

The minimum size of a graph of given order,maximum degree and diameter were investigated by Erd˝os and R´enyi[4],and by Erd˝os,R´enyi and S´os[5].The problem of determining the minimum size of a graph of given order,minimum degree and diameter was solved by Bollob´as[6].Because the conditional diameterD(G;l,s)of a graphGcan not be increased by adding an edge,it is natural to ask what is the maximum number of edges of graphs with given order and conditional diameter.For the casel=s=1,Ore[7]obtained the following result.

Theorem 1[7]LetGbe a connected graph with ordern,sizemand diameterd.Then

Furthermore the bound is best possible.

If the minimum degree is prescribed,Mukwembi[8]obtained the following result.

Theorem 2[8]LetGbe a connected graph of ordern,sizem,diameterdand minimum degree δ(G)=δ ≥2.Then

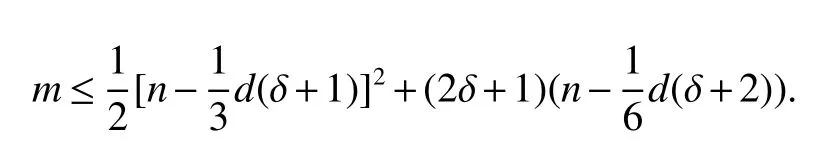
Furthermore,the bound,for fixed δ,is asymptotically tight.

In[9],Ali et al.bounded the size of any graph and of any triangle-free graph in terms of its order,diameter and edgeconnectivity.Balbuena et al.[3] gave the upper bounds of the sizes of graphs with given order and conditional diameter,which generalized Theorem 1.

Theorem 3[3]Letlandsbe integers with 1 ≤s≤l.LetGbe a connected graph with ordern,sizemand conditional diameterD(G;l,s)=d.Then

Furthermore,these bounds are best possible.

Motivated by the results above,we investigate the upper bounds of the sizes of graphs with given order,minimum degree and conditional diameter.Our results extends those in[8].In the next section,we will give our main results.

1 The main results

In this section,we assume thatn,l,sanddare four given integers such that 1 ≤s≤land 1 ≤d≤n+1−(l+s).

LetGbe a graph with ordern,sizemand conditional diameterD(G;l,s)=d.Then by definition,there exist two subsetsL,S⊆V(G)with|L|=land|S|=ssuch thatd(L,S)=d.Ifd=1,thenmand equality holds if and only ifGis isomorphic to complete graphKn.Ifd=2,thenn≥l+s+1.The conditiond(L,S)=2 is equivalent to that there exist two edgeswu,wvwithu∈L,v∈S,w∈V(G)(L∪S),and no edge ofGjoins a vertex ofLand a vertex ofS.Thusmand equality holds if and only ifGis isomorphic to the graph obtained byKnby deleting all edges between two disjoint subsets of vertices with cardinalitieslands.We assumed≥3 in the following.

Theorem 4Letn,l,sanddbe integers such that 1 ≤s≤land 1 ≤d≤n+1−(l+s).AssumeGis a connected graph with ordern,sizem,minimum degree δ ≥2 and conditional diameterD(G;l,s)=d≥3.

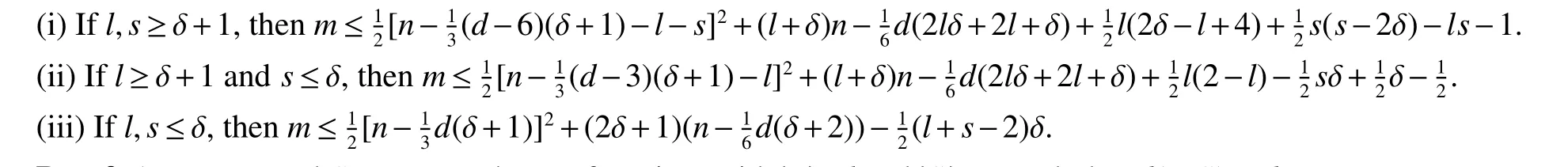
ProofAssumeLandSare two subsets of vertices with|L|=land|S|=ssuch thatd(L,S)=d.LetP:=u0u1u2···udbe a shortest path joiningLandS,whereu0∈Landud∈S.LetA1⊆V(P)be the set

This completes the proof of Theorem 4(iii).And Theorem 4 thus holds.

The upper bound in Theorem 4(iii)forl=s=1 is exact the bound in Theorem 2.Note thatD(G;1,1)=D(G).Thus the results of Theorem 4 implies Theorem 2.

In the following,we will construct some graphs to show that the upper bounds in Theorem 4 are asymptotically tight with given minimum degree.We only construct examples for Theorem 4(i).The examples for Theorem 4(ii)and(iii)can be similarly constructed.

Letd≥3 be an integer withd≡0(mod 3).Letn,δ,landsbe integers such that δ ≥2,δ+1 ≤s≤landd≤n+1−(l+s).We construct a graphGas follows.The vertex setV(G)isV0∪V1∪···Vd,where

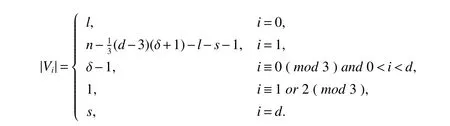
For any two distinct verticesu,v∈V(G),sayu∈Viandv∈Vj,uandvare adjacent inGif and only if|i−j|≤1.We see that|V(G)|=n,δ(G)=δ,D(G;l,s)=dand

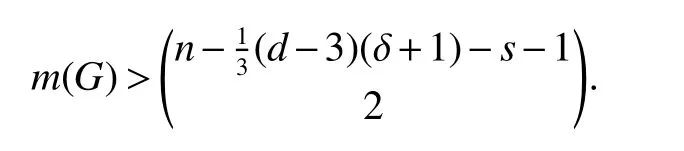
Thus the upper bound in Theorem 4(i)is asymptotically tight with fixed minimum degree.