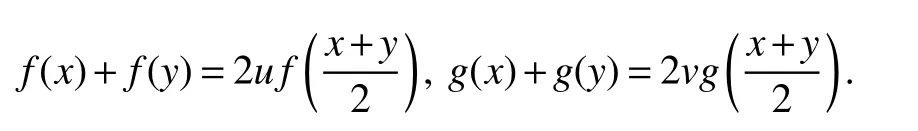Some Logarithmic Submajorisation Inequalities Related to Heinz Mean∗
JIANG Xueyao,HAN Yazhou
(School of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)
Abstract:In this paper,the inequality related to Heinz mean in matrix version is extended to operator version,and some logarithmic submajorisation inequalities related to Heinz means of operator on a semi-finite von Neumann algebra M are presented by using the technique of generalized singular values.There are mainly where 0 ≤x,y ∈M, h >0, f and g are operator concave functions.In addition,other forms of logarithmic submajorisation inequalities are also generalizalied.
Key words:von Neumann algebra;logarithmic submajorisation inequality;measurable operator
0 Introduction
A norm‖|·|‖on Mnis called unitarily invariant if‖|UAV|‖=‖|A|‖for allA∈Mnand all unitary matricesU,V∈Mn,where Mnis the set ofn×ncomplex matrices.For anyA∈Mn,we denote by{sj(A)}the sequence of singular values ofA.The Ky Fank-norms ofA,k=1,2,···,n,are defined as the sum of itsklargest singular values,

LetA,B∈Mn,then the Fan Dominance Theorem tells us by Theorem IV.2.2 of[1]that‖|A‖|≤‖|B‖|for all unitarily invariant norms‖|·‖|if and only if‖A‖(k)≤‖B‖(k),k=1,2,···,n.
LetA,B∈andp,q>0.The well-known inequality for the Heinz means(see,p.265 of[1])says that

Recently,a related inequality to the above Heinz mean inequality was mentioned by Bourin in[2]as follows:
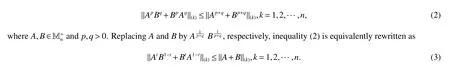
In 2013,Hayajneh-Kittaneh in[3]worked out(2)forp=1,2,3 andq=1 in the case of the Hilbert-Schmidt norm.Bhattia in[4]proved(3)in the case of the Hilbert-Schmidt norm under the conditionIn his investigation of the arithmeticgeometric mean inequality of matrix version,Hayajneh-Hayajneh-Kittaneh in [5] obtain another weaker,but much more general than inequality(3),

whereA,B∈and 0 ≤t≤1.We refer to[6-9]and the references therein for more details on on this topic.
The purpose of this article is committed to generalize the submajorisation inequality(4)to the logarithmic submajorisation version by using the technique in [5,10,11].More exactly,we show that for 0 ≤x,y∈M andfandgare operator concave functions
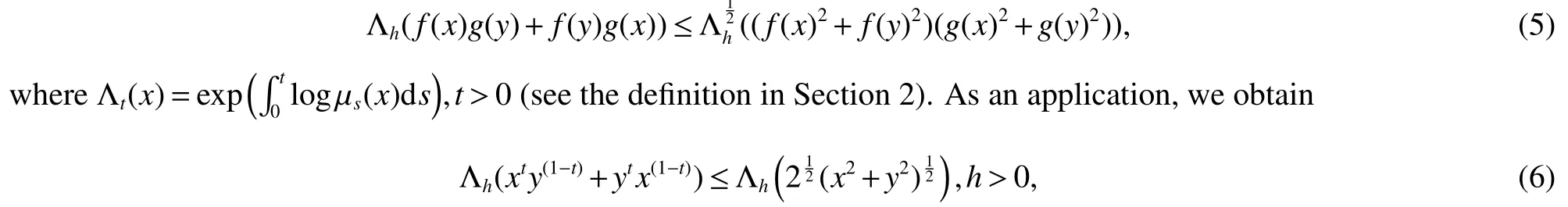
where 0 ≤x,y∈M and 0 ≤t≤1,which is a generalization of the inequality(4).Moreover,we get

where 0 ≤x,y∈M andf,gare two operator concave functions such thatf(x)g(x)=x.
1 Preliminaries
Let M ⊆B(H)be a von Neumann algebra on a separable Hilbert space H.A trace τ on the von Neumann algebra M is a map τ:M+→[0,∞]which is additive,positively homogeneous and unitarily invariant,where M+={x∈M:x≥0}.A trace τ:M+→[0,∞]is referred to as
(1)faithful ifx∈M+and τ(x)=0,thenx=0,
(2)semifinite ifx∈M+with τ(x)>0,then there exists 0 ≤y≤xsuch that 0<τ(y)<∞,
(3)normal ifxi↑i xin M+,then 0 ≤τ(xi)↑iτ(x).
In what follows,we will keep all previous notations throughout the paper,and M will always denote a semifinite von Neumann algebra acting on a separable Hilbert space H,with a normal faithful semifinite trace τ.We refer to[12]for von Neumann algebras.
Definition 1Letx∈M andt>0.The generalized singular numberµt(x)is defined by

We will denote simply by λ(x)andµ(x)the functionst→λt(x)andt→µt(x),respectively.
Next,we will use the following definitions:letx,y∈M,then we say thatxis submajorized byy,denoted byxy,if and only if

Ifx∈M,then we can define

Letx,y∈M,then we say thatxis logarithmic submajorisation byy,denoted byx≺log y,if and only if

See[10,13]for basic properties and detailed information onµ(x)and Λ(x).
2 Main results
A positive functionfon[0,∞)is called operator concave if

for allx,y∈M.
We start with some lemmas which will be used in our proof.
Lemma 1Letx,y∈M,xandybe self-adjoint operators.Then

ProofIt is clear obvious that according to the inequality(x−y)2=(x−y)∗(x−y)≥0.
From the fact thatf(x)=xt(0 ≤t≤1)is operator concave on M we can obtain the following result.
Lemma 2Let 0 ≤x,y∈M and 0 ≤t≤1.Then

Lemma 3Let 0 ≤x,y∈M and let 0 (see[10,p.288]). Now we are ready to present the main result. Theorem 1Let 0 ≤x,y∈M.Iffandgon[0,∞)are operator concave functions,then ProofLet According to Lemma 2.5 of[10]and Lemma 3,we obtain Corollary 1Let 0 ≤x,y∈M and 0 ≤t≤1.Then Proof(1)From Lemma 2 and Theorem 1 we obtain (2) Ifx,y≥0,then µt(xy)=µt((xy)∗)=µt(y∗x∗)=µt(yx).We can draw a conclusion from the definition of Λ(x) and the properties ofµ(x)that Hence,by Lemma 2,we get Corollary 2Let 0 ≤x,y∈M and 0 ≤t≤1.Then ProofSincef(t)=ept,p>0,is a convex functions,the result is based on Corollary 1 and applying Theorem 2 of[15]. In this section,we will consider another version of logarithmic submajorisation which related to(4). Theorem 2Let 0 ≤x,y∈M.Iffandgare two positive operator concave functions such thatf(x)g(x)=x,then ProofAccording to properties of operator concave function,we have Then there exist contraction operatorsu,v∈M such that From Lemma 2.5 of[10]we have Corollary 3Let 0 ≤x,y∈M and 0 ≤t≤1.Then ProofBy Theorem 4.2 of[10],Lemma 2,Lemma 3 and equation 8,we have Proposition 1Let 0 ≤x,y∈M and 0 ≤t≤1.Then ProofFrom Lemma 1,Lemma 2,equation 8 and Theorem 2.5 of[10]we obtain

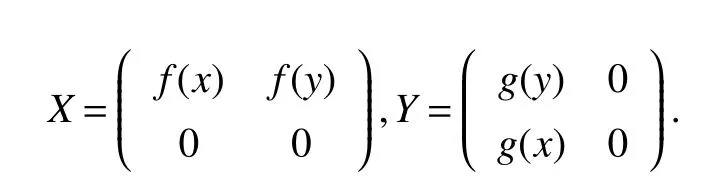






3 Related logarithmic submajorisation inequalities