给定点数，最小度和条件直径的图的边数的上界∗

马花萍，田应智

(新疆大学 数学与系统科学学院，新疆 乌鲁木齐 830046)

0 引言

本文中没有定义的图论术语和符号,请参考文献[1],在这篇文章中主要研究的是有限简单图.设G 是一个顶点集为V(G),边集为E(G)的图,图G 的阶n=|V(G)|为其顶点的数目,m=|V(G)|为其边的数目.对于V(G)中的每一个点v ∈V(G),NG(v)表示与点v 相邻的所有的顶点的集合,用NG(v)表示v 的邻点集,并且dG(v)=|NG(v)|称为图G 中点v 的度数.用δ(G)表示图G 的最小度.对于两个不交的点子集V1和V2,[V1,V2]G表示图G中所有边的集合,连接了点集V1和V2中的点.取任意数x,其中x表示x 取上整数,即为不小于x的最小整数,x表示x 取下整数,即为不超过x 的最大整数.

任意两个点u 和v 之间的距离dG(u,v)定义为图G 中从点u 到v 的最短路的长度.对于连通图G,定义其直径D(G)为max{dG(u,v):u,v ∈V(G)},如果图G 不连通,则D(G)=∞.设V1⊆V(G)和V2⊆V(G) 是V(G)的两个非空点子集,用d(V1,V2)表示u ∈V1和v ∈V2之间的最短距离dG(u,v).为减少歧义,本文用N(v),d(v),[V1,V2],d(u,v)和d(V1,V2)表示NG(v),dG(v),[V1,V2]G,dG(u,v)和dG(V1,V2).

Balbuena等人在文献[2]中推广了直径,介绍了图G 的条件直径,给定条件P 使得V(G)中至少有一对非空点子集(V1,V2)满足给定的条件P,条件直径DP(G)定义为max{dG(V1,V2):∅/=V1,V2⊆V(G),其中(V1,V2) 满足条件P}.由于条件直径是测量具有给定条件的顶点子集之间的最大距离,因此它们可以用于某些需要控制特定网络群集之间的通信延迟.

设l 和s 是两个整数且满足1 ≤s ≤l.考虑P 满足下面条件:(Vl,Vs)⊆V(G)×V(G)满足P 当且仅当|Vl|=l和|Vs|=s.在这种情况下,文献[3]中用D(G;l,s)来表示条件直径DP(G),即

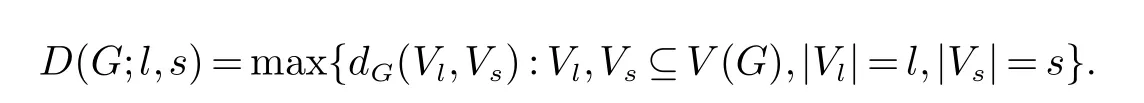
注意到D(G;1,1)恰好为图的直径D(G),并且当D(G;l,s)=0 时当且仅当l+s>|V(G)|.同时当l+s ≤|V(G)|时有D(G;l,s)≤|V(G)|+1−(l+s).

给定点数,最大度和直径条件下图的边数下界是由Erd˝os和R´enyi在文献[4]以及Erd˝os,R´enyi和S´os在文献[5]中给出的.给定点数,最小度和直径条件下图的边数下界由Bollob´as在文献[6]中给出的.由于图G 添加一条边其条件直径D(G;l,s)不会增加,因此很自然的就会问给定点数和条件直径下图的边数上界.当l=s=1 时,Ore在文献[7]中得到下面的结果.

定理 1[7]设G 是一个点数为n,边数为m 和直径为d 的连通图.则

同时这个界是最优的.

如果给定最小度,Mukwembi在文献[8]中得到下面的结果.

定理 2[8]设G 是一个点数为n,边数为m,直径为d 和最小度为δ(G)=δ ≥2 的连通图.则

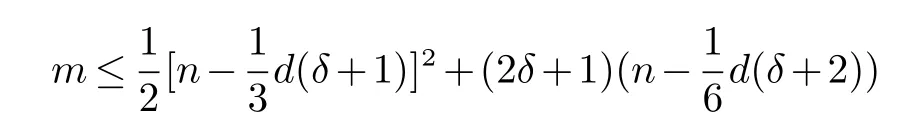
同时对于给定的δ 这个界是渐进紧的.

在文献[9]中,Ali等人给出对任意无三角形图限制其点数，直径和边连通度的边数的界.Balbuena等人在[3]中给出给定点数和条件直径的图的边数上界,这个结果推广了定理1.

定理 3[3]令l 和s 为整数且1 ≤s ≤l.设图G 是一个点数为n,边数为m,条件直径为D(G;l,s)=d 的连通图.则

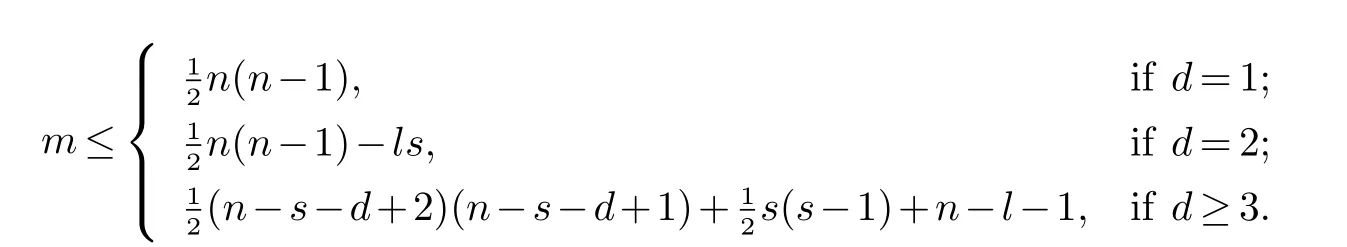
并且这些界是最优的.

根据以上结果本文给出了给定点数，最小度和条件直径下图的边数上界,本文推广了文献[8]的结果.

1 主要结果

在本节中,假设n,l,s 和d 是四个给定的整数,使得1 ≤s ≤l 和1 ≤d ≤n+1−(l+s).

设图G 的点数为n,边数为m，条件直径为D(G;l,s)=d.由条件直径的定义可知,存在两个子集L,S ⊆V(G)其中|L|=l 且|S|=s,使得d(L,S)=d.当d=1 时m其中等式成立当且仅当G 同构于完全图Kn.当d=2 时n ≥l+s+1,G 的条件直径d(L,S)=2,即存在两条边wu 和wv，其中u ∈L,v ∈S 和w ∈V(G)(L∪S),并且在L 和S 之间没有边,即没有一条边的一个点在L 中,另一个点在S 中,因此其中等式成立当且仅当G 同构于完全图Kn删除基数为l 和s 的两个不相交的点子集之间的所有边.因此下面讨论d ≥3的情况.

对任意的u,v ∈A1有d(u,v)≥3.故

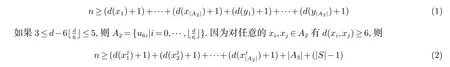
其中j=1,2,···,δ.对任意的yi,yj∈A3有d(yi,yj)≥6,则

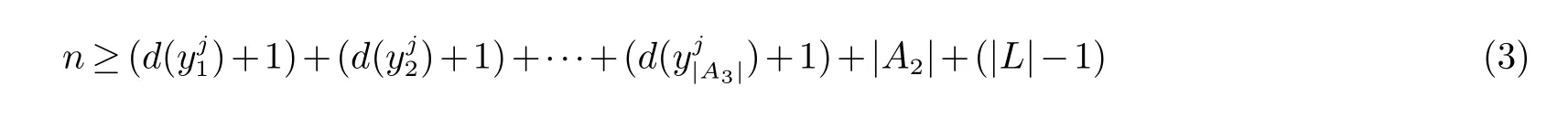
其中j=1,2,···,δ.

对式(1)和(2)求和得

对式(1)和(3)求和得

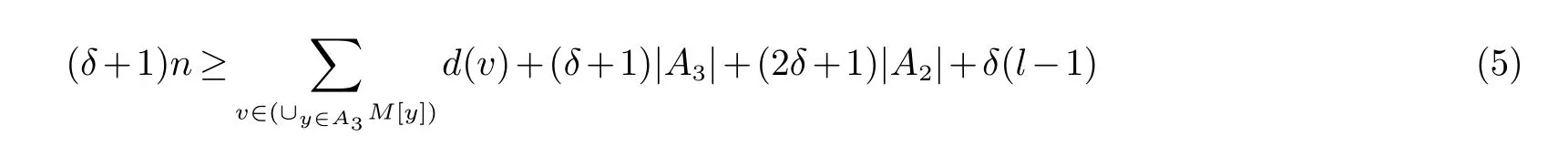
由式(4)和(5)式可得

其中j=1,2,···,δ.对任意的yi,yj∈A3有d(yi,yj)≥6,则

其中j=1,2,···,δ.

对式(1)和(6)求和得

对式(1)和(7)求和得

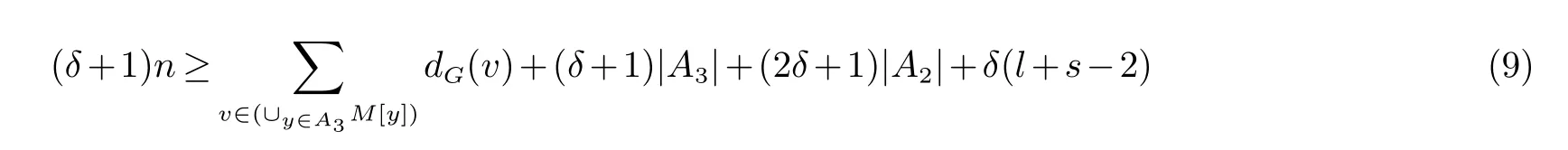
同样地,由式(8)和(9)可得

断言1 已证.

因为L′中的每一个点都在A∪L′中至多有l−1 个邻点,S′中的每一个点都在A∪S′中至多有s−1 个邻点,且由于d(L,S)=d ≥3,则R 中不存在一个点的邻点既在L′中也在S′中,故

这就证明了定理4(iii).定理4 证毕.

注意到D(G;1,1)=D(G),定理4 与定理2 相同.即当l=s=1 时,定理4(iii)的上界恰好等于定理2 的上界.

下面证明在给定点数,最小度和条件直径下构造图证明定理4 的上界是渐进紧的.这里只讨论定理4(i)的情形,(ii) 和(iii)的情况与(i)的类似,就不在重复说明.

设d ≥3 为整数,且d ≡0 (mod 3).令n,δ,l 和s 为整数,使得δ ≥2,δ+1 ≤s ≤l 和d ≤n+1−(l+s).构造点集划分为V(G)=V0∪V1∪···Vd的图G 如下:

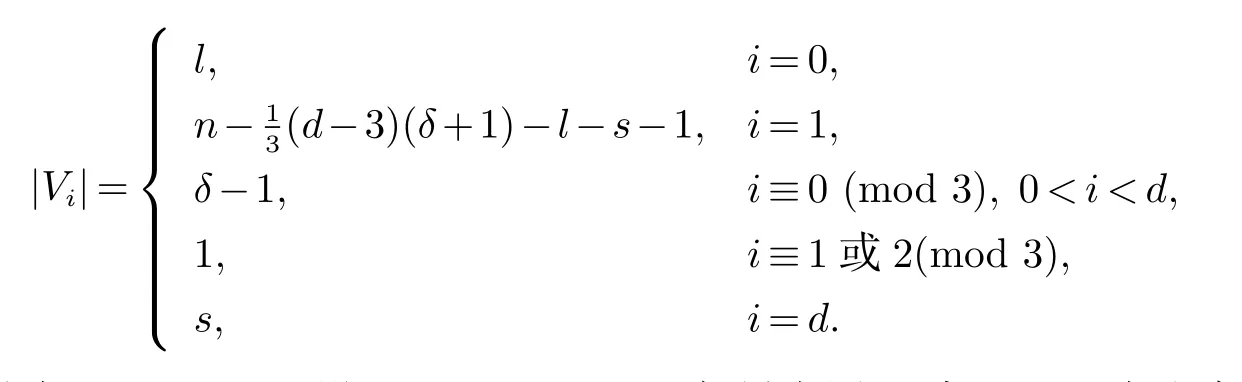
对任意两个不同的点u,v ∈V(G),设u ∈Vi和v ∈Vj,如果在图G 中u 和v 有边当且仅当|i −j|≤1,则|V(G)|=n,δ(G)=δ,D(G;l,s)=d 和

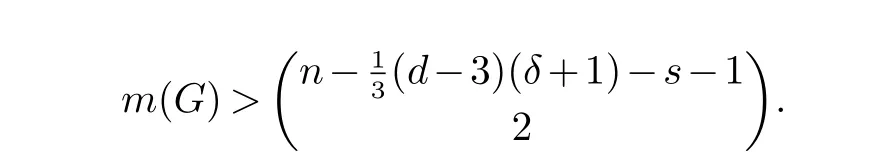
即对给定的最小度定理4(i)的上界是渐进紧的.