基于分数阶季节性灰色模型的交通流预测

沈琴琴，张智杰，齐绪存，岳心怡

（1.南通大学杏林学院，江苏 南通 226236；2.南通大学 交通与土木工程学院，江苏 南通 226019）

交通拥堵已成为城市发展的瓶颈，智能交通系统作为缓解交通拥堵的有力手段受到了广泛关注。准确、实时的交通流预测是该系统高效运行的关键[1-3]。交通流是指在单位时间内，通过道路某一段面的交通实体数。根据时间间隔的划分，交通流可分为长时、中长时和短时，一般将5～30 min 的交通流称为短时交通流。由于城市路网之间的高度时空融合特征和人类出行行为的不规律性，导致短时交通流数据通常具有很强的随机性、非线性、季节性等特征，给这类问题的高精度拟合和预测带来很大的挑战[4-10]。针对这些特征，肖新平等[11]将文献[12]中提出的截断累加生成长子引入到城市道路短时交通流的预测中，并结合灰色建模的思想，提出了一类季节性滚动GM（1，1）模型（seasonal rolling grey model，SRGM（1，1））。研究表明，该算子能有效地弱化短时交通流数据的随机性和季节性特征，且新的季节性GM（1，1）模型比季节性离散GM（1，1）模型（seasonal discrete grey model，SDGM（1，1））、小波神经网络、自回归滑动平均等模型的预测精度更高。沈琴琴等[13]在此基础上提出了一类基于复化Simpson 公式的季节性灰色Fourier 模型，进一步提高了模型的精度和适用性。吴利丰等[14-15]基于新信息优先的原则，提出了分数阶累加生成方式，并结合灰色建模技术提出了分数阶GM（1，1）模型（fractional grey model，FGM（1，1））、自适应智能分数阶GM（1，1）模型、加权分数阶模型等[16-18]，极大地提高了灰色预测模型的精度。

本文提出了一种新的分数阶季节性GM（1，1）模型（fractional seasonal grey model，FSGM（1，1））。该模型首先对交通流数据进行分数阶截断生成累加以弱化数据的季节性和随机性；然后，采用GM（1，1）模型的思想进行建模，并运用粒子群优化算法来寻求最佳阶数以获得最优预测精度；最后，将新的模型应用于江苏省南通市一组城市道路短时交通流数据进行模拟仿真，数值结果表明新模型比SRGM（1，1）、FGM（1，1）和SDGM（1，1）具有更高的精度，适用于实际问题的计算。

1 分数阶截断累加生成算子

设一组具有季节性波动（周期为q）的非负原始序列为

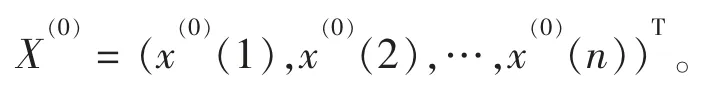
首先根据季节性波动的周期q 对其截断累加，得到截断累加生成序列

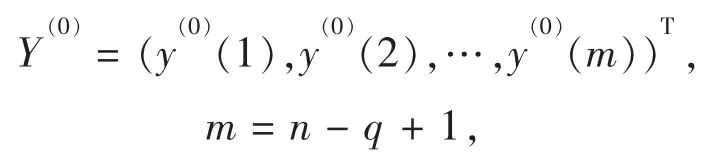
2 分数阶季节性GM（1，1）模型

本节给出FSGM（1，1）模型的建模过程，最优阶数的确定及模型步骤。

2.1 FSGM（1，1）模型的建立

定义1设非负原始序列为

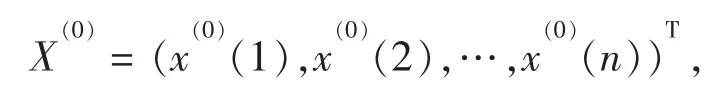
分数阶截断累加生成后序列为

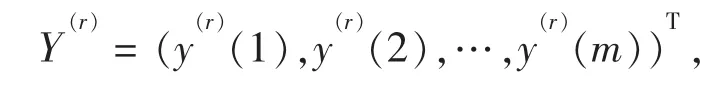
如式（1），其均值生成序列为

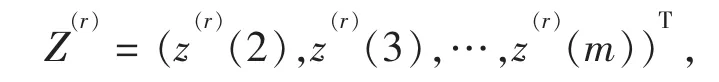
其中

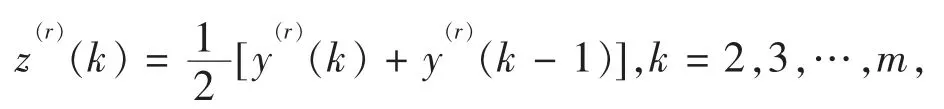
FSGM（1，1）模型的白化微分方程定义为

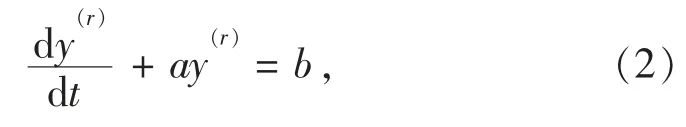
其离散方程为

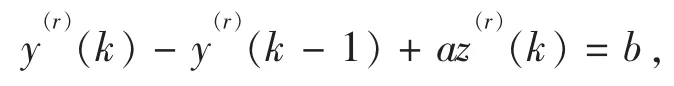
其中参数a，b 分别为发展系数和灰作用量，可由最小二乘法求得

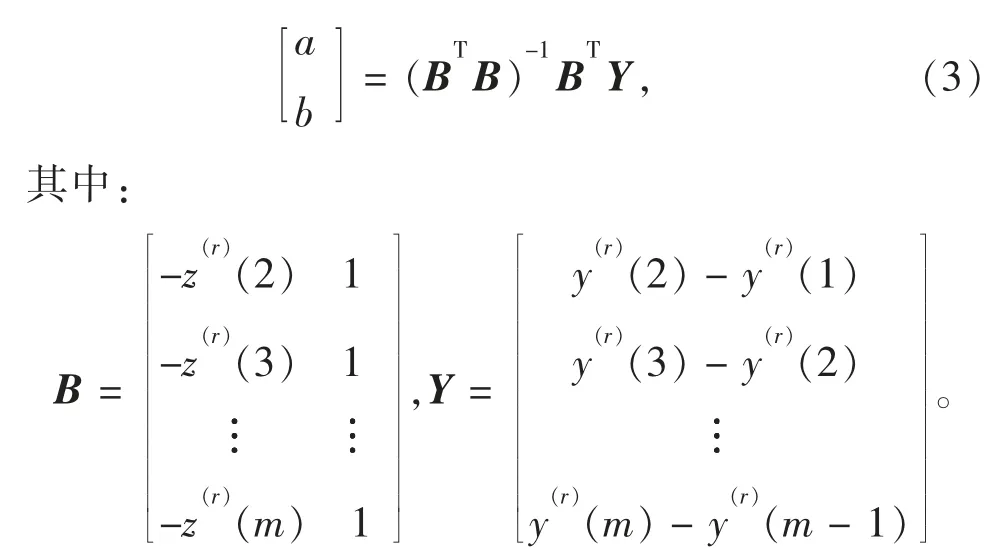
以（1，y（0）（1））为初始条件，根据微分方程（2）的解可得FSGM（1，1）模型的时间响应式

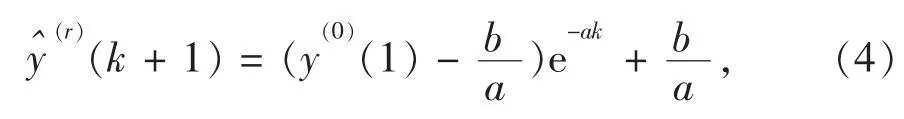
对式（4）得到的序列进行分数阶累减，可得

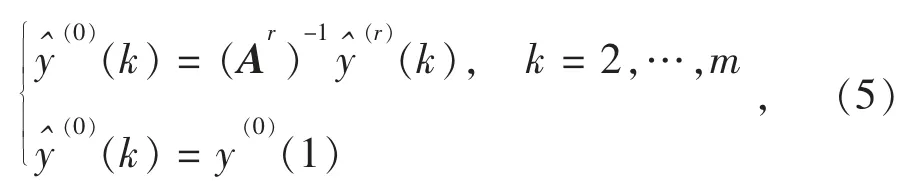
进而截断累减还原得到原始数据预测值为

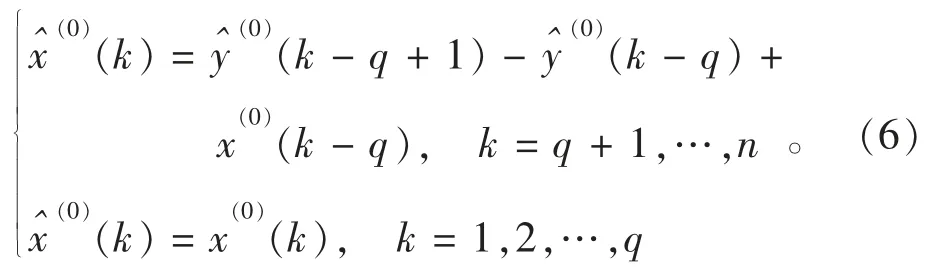
2.2 粒子群优化算法确定最优阶数

分数阶累加参数r 不仅能有效地体现新信息优先原则，还能极大地提高模型的拟合和预测精度。为了确定最优阶数r，本文采用了具有普适性的粒子群优化算法，并取拟合数据的平均绝对百分比误差（mean absolute perenct error，MAPE）为适应度函数

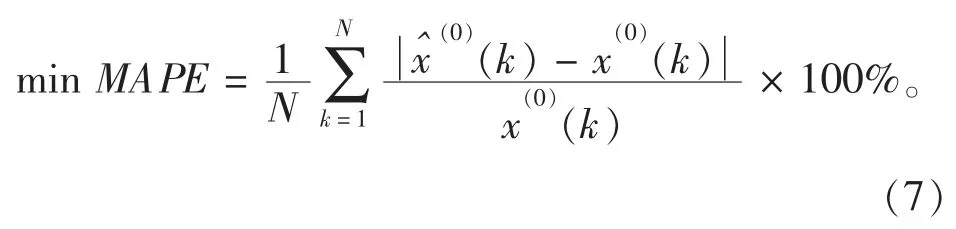
粒子群算法[19-20]从若干组随机解出发采用一个适应度函数来判断各组解的优劣，并通过不断迭代得到适应度更高的解，迭代结速后适应度最高的解即为最优解。粒子的位置和速度更新公式分别为

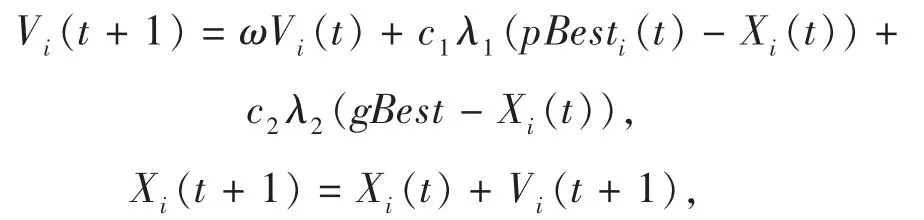
其中：ω，c1，c2为自定义常数；λ1，λ2是在[0，1]内的随机数；pBesti（t）表示粒子i 在第t 次迭代中的局部最优解；gBest 是指粒子i 经过前t 次迭代后得到的全局最优解；Vi（t）为粒子i 在第t 次迭代时的速度（Vi（1）为任意实数）；Xi（t）为粒子i 在第t 次迭代时的位置，Xi（1）由r 的取值范围确定

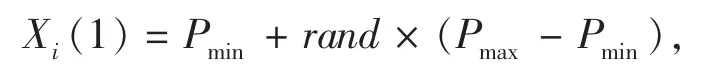
其中Pmin和Pmax分别是r 取值范围的下限和上限。

本文中，选取ω=0.8，c1=c2=2。一共设置了50 组初始解，迭代次数设置为3 000。每次迭代都会产生一个局部最优解pBest，即为该次迭代中的最优累加次数。将其代入式（7）计算适应度，当低于gBest 的适应度时，用pBest 代替gBest，否则不变。直到迭代完成后，最终的gBest 即为所求分数阶r 的全局最优解。图1 给出了利用粒子群优化算法确定最优阶数的流程图。

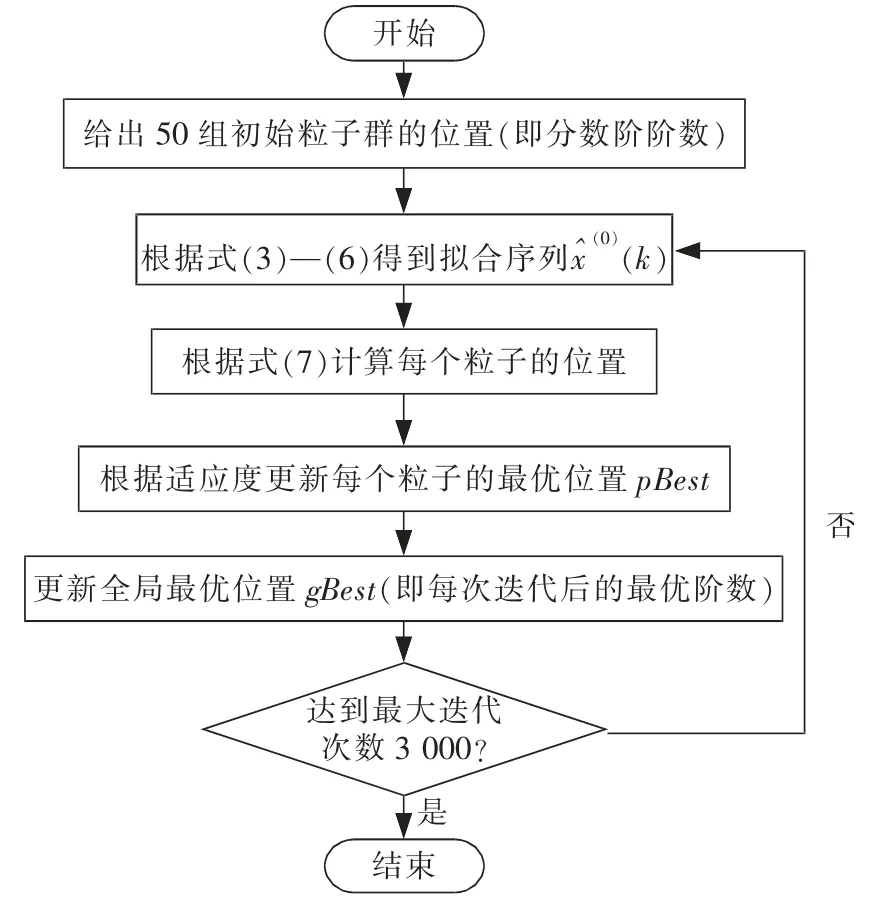
图1 粒子群算法确定最优阶数的流程图Fig.1 Flowchart for determining the optimal order by PSO algorithm

2.3 模型步骤

FSGM（1，1）模型建立步骤如下：

步骤1根据原始序列x（0）的周期及分数阶r 的初始值，进行截断累加生成得到新序列y（r）；

步骤2通过最小乘算法得到式（3）中参数a，b，代入式（4）—（6）中计算得出拟合序列x^（0）；

步骤3采用粒子群算法以式（7）为适应度函数求解出最优累加次数；

步骤4重复步骤1、步骤2 得到预测序列。

3 实例分析

3.1 数据来源

案例选用江苏省南通市钟秀中路到北濠桥路口的东直行道路断面2018 年8 月12 日至9 月1日上午7∶00—7∶30 一共21 d（3 周）的短时交通流数据，详见表1。数据来源于南通市交巡警支队。

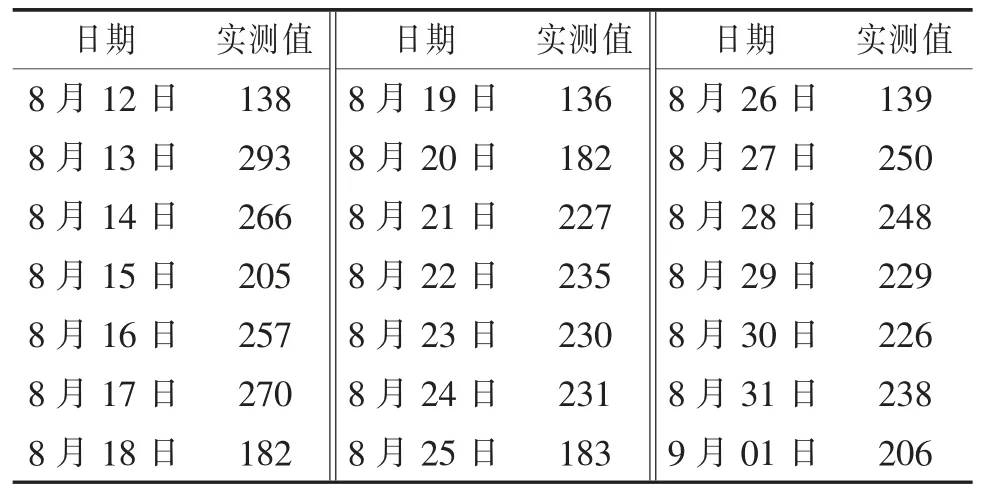
表1 交通流数据Tab.1 Traffic flow data辆·30-1 min-1

3.2 预测结果分析

本文将原始序列中前14 组（前两周）数据作为拟合数据分别代入SRGM（1，1）模型[12]，FGM（1，1）模型[14]，SDGM（1，1）模型[11]和本文提出的GSGM（1，1）模型求解出相应参数，将求解出的参数代入各自的模型预测后7 d（最后一周）的数据。在模型计算中，截断累加周期q 取7，取平均绝对百分比误差（7）作为评价指标。FGM（1，1）和FSGM（1，1）模型在计算中都需要确定最优阶数r，为保证两种模型具有可比性，在确定r 时均采用粒子群算法，经计算得到FGM（1，1）和FSGM（1，1）模型最优阶数r 分别为1.200 2 和1.142 2。在4 种模型中，仅有FGM（1，1）模型可以得到前7 组数据的拟合误差，其他模型由于进行了季节性累加，前7 组拟合数据均为精确值，因此4 种模型都只比较8～14 d 的拟合误差，相应结果见表2 及图2。

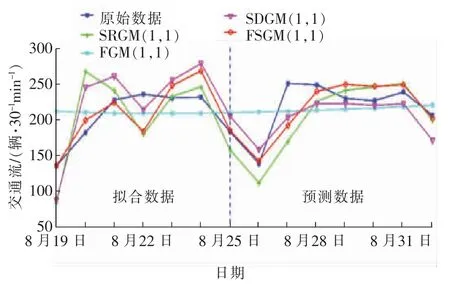
图2 原始数据与4 种模型的拟合与预测数据比较Fig.2 Comparison between the original data and the fitting and prediction data of four models

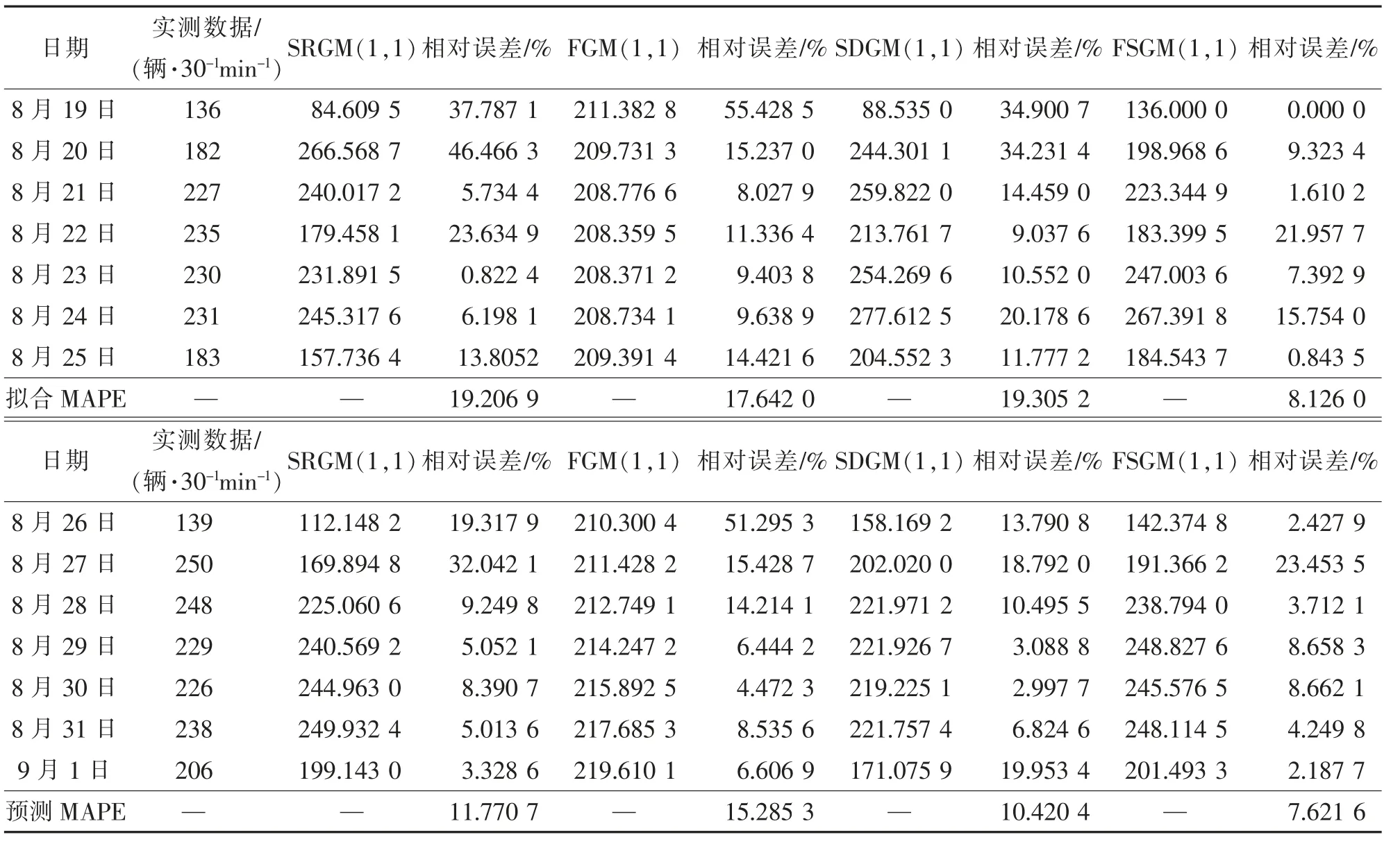
表2 4 种模型预测结果及误差的比较Tab.2 Comparison of prediction results and errors of four models

由计算结果可知，本文提出的FSGM（1，1）模型的拟合误差为8.126 0%，与其他3 组预测模型中最小拟合误差17.642 0%相比，精度有了大幅度提高。在预测数据方面，FSGM（1，1）模型的预测误差为7.621 6%，而其他3 种模型的预测误差都在10%以上。由此可见，本文提出的FSGM（1，1）不仅在拟合数据上有很高的精度，而且在预测数据上同样具有很高的预测精度，适用于实际问题计算。

为了说明分数阶累加参数对新模型拟合和预测精度的影响，图3 给出了不同的分数阶累加参数r（0.1～1.3）和FSGM（1，1）模型拟合及预测精度之间的关系。特别地，当r=1 时，FSGM（1，1）模型退化为已有的SGM（1，1）模型。从图3 中可以看出，分数阶累加参数r 对新模型的拟合和预测误差的影响十分明显。选取合适的分数阶累加参数r，本文所提出的FSGM（1，1）预测模型不仅能提高拟合精度，还能较精确地预测下一阶段的交通流量。

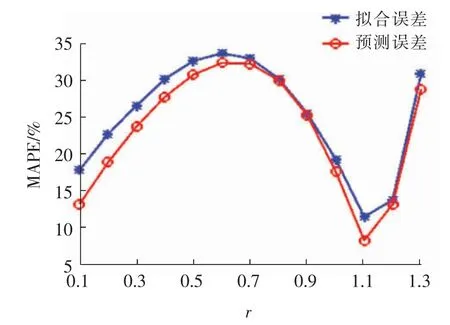
图3 分数阶阶数与拟合误差、预测误差关系图Fig.3 Relation diagram of fractional order,fitting error and prediction error

4 结论

本文利用城市道路某一段面交通流数据在以周为单位变化时呈现出明显的周期性特征，从数据预处理的角度和灰色建模技术的信息优先原则，首先提出了一种季节性截断累加生成算子，并利用GM（1，1）预测模型的思想，提出了一种新的分数阶季节性GM（1，1）模型，给出了预测模型的计算公式，并采用粒子群优化算法确定出最佳分数阶累加参数。通过实例比较分析，本文提出的分数阶季节性GM（1，1）模型在城市道路短时交通流预测中具有较高的精度，值得在实际交通流预测中加以应用。