非线性热学:基于温度响应性的热超构材料设计
戴高乐,黄吉平
(1.复旦大学 物理学系,上海 200438;2.南通大学 理学院,江苏 南通 226019)
非线性现象可以表述为系统的反馈对输入参数的非线性依赖[1],如物体形变在一定条件下偏离胡克定律,或者介质极化强度可能与电场强度的高次项相关。非线性现象在数学上对应非线性的微分方程。区别于线性方程,非线性方程的解不满足线性可加性,尤其在强非线性下对初始条件十分敏感,求解往往非常困难,流体力学中著名的Navier-Stokes 方程组即是一例。但正如一枚硬币的两面,从复杂的非线性方程或者说非线性系统中往往能发现各种新奇的现象,如混沌、孤波、分形、激波与多稳态。非线性现象受到重视始于天体力学中三体问题的不可解性,此后在动力系统、气象学、生命科学等领域非线性现象都成为重要课题。而在传统物理学领域,光、电、声中的非线性效应已经被广泛研究与应用,如非线性光学[2]、非线性声学[3]都已经成为专门学科,而以电子整流、磁滞现象等非线性效应为基础的电子计算、存储器件更是深刻影响了人类的生产生活。相比之下,在物理学中另一基本领域热学中,还尚未形成一门公认的“非线性热学”子学科,而各种基于非线性效应的热学功能器件相比它们的电学同类还尚未发展成熟。考虑到对热现象的调控已经成为提高能源利用效率、对微观器件到宏观设施在各尺度进行热管理的重要手段,“非线性热学”无疑值得关注与发展[4]。
套用列夫·托尔斯泰的话说,“线性关系是相似的,非线性关系各有各的非线性”,于是首先要问,“非线性热学”中的非线性关系主要指的是什么?这一问题其实不易直接回答,因为传热涉及到3 种不同的基本机制,即传导、对流与辐射。尽管如此,我们可以首先将精力放在相对研究得最多的热传导上。宏观介质中的热传导一般可以由经典的傅里叶定律描述:j=-kΔT,其中:j 是热流密度矢量;k是材料热导率;T 是温度;Δ是梯度算符。结合热流连续性条件,如果各参数都为常数,此时传热方程是关于温度的线性方程,其中:t 是时间;ρ 是材料密度;C 是比热。当传热为稳态时,可知热导率为材料本身唯一影响传热的属性。如果直接类比非线性光学中极化率或电导率与电场强度或其高次项的依赖关系(即非线性电极化理论),则应当设想“非线性热学”中热导率对温度梯度有响应。不过实际材料中发现的多是热导率对温度的各种直接依赖关系,此时傅里叶定律为非线性微分方程。热导率对温度的典型依赖关系即幂次关系Tα,根据Dames 的总结,部分实际材料中α 的取值可以从-3.5 到5.4 不等[5]。而根据动理学,高温下的介电体热导率与T-1成正比(即Eucken 定律),低温下与(-T-1)呈e 指数关系,而气体热导率近似正比于
还有另一种“逆向”的研究思路,即直接从功能器件具备的非线性效应出发去设计相应的材料结构,实际上这也是目前对热学中非线性效应研究的主要范式。热学功能器件主要的模仿对象是电学。非线性效应在电学中的核心效应即整流,这是二极管、晶体管等电子计算元器件的基础。无论具体的实现机制如何,电流的整流效应意味着关于零偏压非对称的伏安特性曲线,对应到热学中即关于零外部温差非对称的温度差-热流曲线,这样的曲线一般不是直线,内蕴了对温度(差)具有依赖关系的热导或热阻,即一种非线性热导率。整流一般需要两个条件:非对称的结构及非线性的阻抗。早在1935年,Starr 在研究铜及铜氧化物异质结构的电子整流实验中就同时发现了热整流现象[7],此后数十年间研究人员也发现了多种其他热整流机制[8-9]。但直到本世纪初,随着纳米技术的发展,对低维非线性晶格中声子热整流效应的成功研究[10]才引发了对此领域的巨大关注(关于热整流研究论文数量随时间的变化,可参见Roberts 与Walker 的综述[8])。Starr 的研究中金属材料的热载流子主要为电子,而电的绝缘体与半导体材料中主要的热载流子是声子,即晶格的集体振动模式。整个晶格的哈密顿量包括原子间的相互作用及环境外加的基底势。若将原子间的相互作用近似为简谐振子,即没有声子间的相互作用,则晶格线性。非线性晶格的构造可以从两方面考虑。一方面,将原子间的简谐相互作用替换为非简谐力,即考虑声子间相互作用,如最简单的三声子散射过程。著名的FPUT(Fermi-Pasta-Ulam-Tsingou)模型即属于此类没有基底势或者说动量守恒的非线性晶格。另一方面,可以在简谐振子相互作用的基础上考虑加上某些基底势,常用的FK(Frenkel-Kontorova)晶格即具有周期性基底势的此类非线性晶格。对非线性晶格导热的早期关注来自于对正常热传导(热导率不随尺寸变化,最简单的反例即一维线性晶格)的微观动力学机制的研究[11-12]。而从调控传热的角度出发的首个重要工作来自2002 年Terraneo 等[13]对一维非线性晶格中热整流效应的研究,他们利用谐振子加上非均匀的Morse 基底势设计了3 段结构的非线性晶格,得到了明显的整流效果。此后Li 等[14]利用耦合的两段不同参数的FK 晶格优化了整流效果,设计了热二极管,并指出非线性晶格对温度依赖的声子能谱在接触面的不匹配是整流的关键[14-15]:交换体系两端温度差时,不同结构的能谱会从交叠(在利于导热)变为非交叠(阻碍导热),从而实现热导率的方向性变化。在此基础上,利用非线性晶格的热晶体管[16]、热逻辑门[17]、热存储器[18]等热计算元器件及热抽运[19](shuttling,即无外部温差时的热输运)器件也被设计出来。此后这种基于微观声子热整流的研究对象也从规则的晶格扩展到复杂网络结构[20-21]。而在实验上,基于准一维材料(修饰过的非均匀碳纳米管或氮化硼纳米管)的热整流器也被制备出来(归因于非线性体系中的孤子输运),最高整流比可以达到7%左右(这里整流比定义为两方向热流差与其中更大热流之比)[22]。
然而因为很难精准匹配理论要求的声子谱,实际材料制备的微纳尺度热二极管的整流比往往并不高[23],这也促使部分研究者回到宏观尺寸的体材料,在经典傅里叶定律框架下设计热二极管。Hu 等[24]研究了FK 晶格与φ4晶格的热导率对温度的依赖关系,发现这两段晶格可以组成热二极管,并考察了对应的实际宏观材料,如石英与钻石。Peyrard[25]指出对温度T 与空间x 同时变化的热导率κ(x,T)是产生整流的条件(且热导率不可写成空间函数与温度函数之积,即不可分),而最简单的例子即两段热导率对温度具有不同依赖关系(且不成比例关系)的均匀材料组成的非对称结构,他也考察了该结构相对应的非线性晶格模型。Go 等[26]则进一步指出不可分的温度与空间变化的热导率只是整流的不充分条件,而可分性一定导致整流效应的缺失。需要指出这种对不可分性的分析基于一维且没有内部热源的热传导体系。Dames[5]计算了由两种热导率对温度具有不同幂次关系(正比于Tn1或Tn2)的材料组成的准一维热二极管的整流比λ,在两端温差(高温源TH,低温源TL)不大的情况下其上限满足实验上,用两种钙钛矿氧化钴材料LaCoO3、La0.7Sr0.3CoO3(热导率分别对温度呈现二次与三次多项式关系[23])实现了毫米级别的热二极管,两个方向的热流比为1.43,即30%左右的整流比[27]。可以看出,使用具有温度响应热导率或者说非线性的体材料进行热整流的设计也相当有效。而在整流效应之外,如何利用非线性体材料设计更多的热调控功能器件这一问题也启发研究者将非线性材料引入热超构材料的设计中。
热超构材料[28-30]具有自然材料所不具备的热学性质,是近十余年来兴起的利用人工结构调节热流输运的领域,始于2008 年Fan 等[31]在热传导上建立变换理论并预言热隐身斗篷的存在。此后,随着理论及实验制备技术的发展,各种具备新奇功能的热学调控器件如热聚集器[32]、热旋转器[32]、热透镜[33]、热变色龙[34]、热放大器[35]等相继出现。值得注意的是,大多数研究中涉及的材料都没有考虑自身热导率对温度或者其他环境因素的响应,即线性导热材料。要将非线性因素,或者更具体的说,热导率对温度的依赖关系引入热超构材料的研究,促使研究者从两个方面思考。一方面,原有的理论方法与结构设计是否能继续应用于非线性导热情形?另一方面,当考虑非线性的热导率之后,是否能通过新的理论或结构来设计具备新的调控功能的热学器件,并且这些功能是线性热导率所不能实现的?在本文中我们将介绍利用温度响应性(包括材料热导率自身直接的非线性及材料结构对温度的响应等其他机制导致的非线性热导率)设计、制备热超构材料的相关进展,涉及的方法与所实现的热学调控功能既有对线性导热框架下热超构材料的继承,更有所扩展与突破。
1 非线性变换热学
变换理论是设计超构材料的主要方法之一,首先被应用于电磁波的调控[36-37],核心思想即通过设计特定的材料属性模仿时空弯曲的效果。在热学中,变换理论首先被应用于线性热传导框架[31,38]。2015年,Li 等[39]将变换理论拓展到稳态非线性热传导情形,证明了控制方程在任意坐标变换下具有形式不变性。此时热导率可以与温度相关,即κ(T)。Li 等[40]在此后将这一结论扩展到瞬态非线性热传导情形。
1.1 热隐身斗篷
这一结论首先意味着此前基于线性导热材料设计的变换理论设计的各种器件可以直接扩展到非线性导热材料中,如热隐身斗篷,见图1。热隐身斗篷通常被覆盖在某一物体上,使得斗篷内的该物体不会影响斗篷外背景的温度分布,宛如斗篷内的物体不存在一样。设计隐身斗篷在二维情形下常用的几何变换(r,θ)→(r′,θ′)为
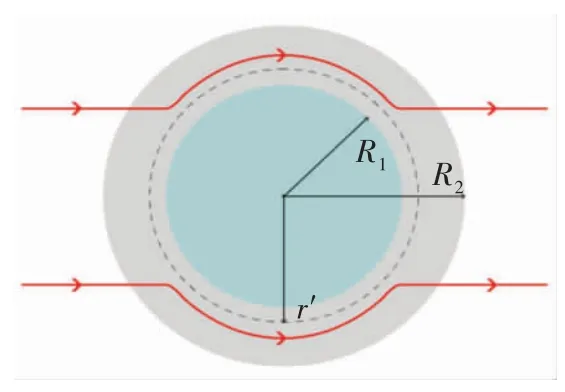
图1 热隐身斗篷的示意图[39]Fig.1 Schematic graph of a thermal cloak[39]
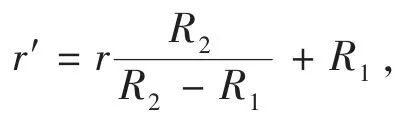
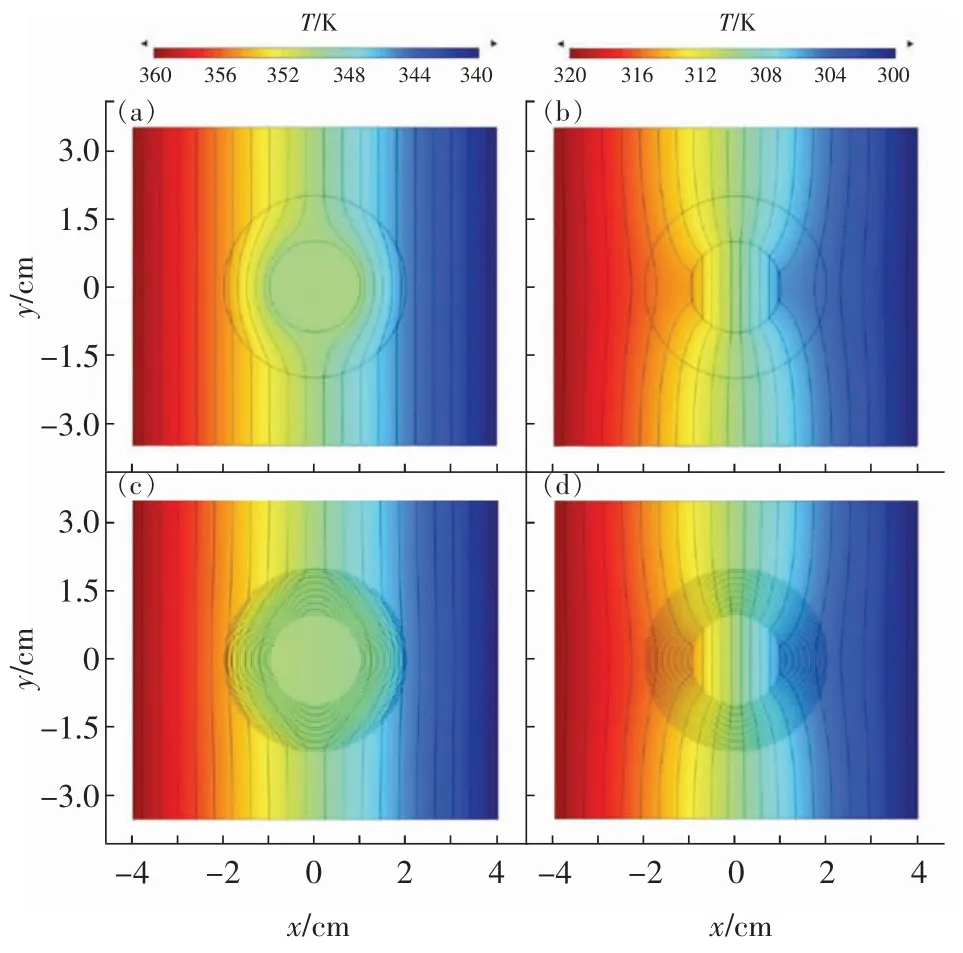
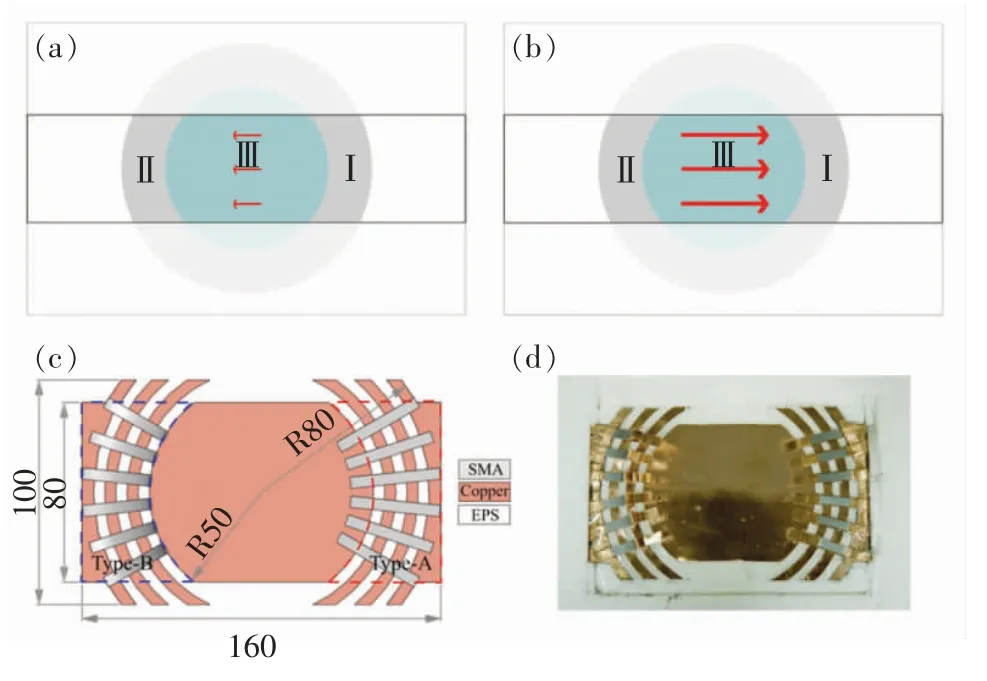
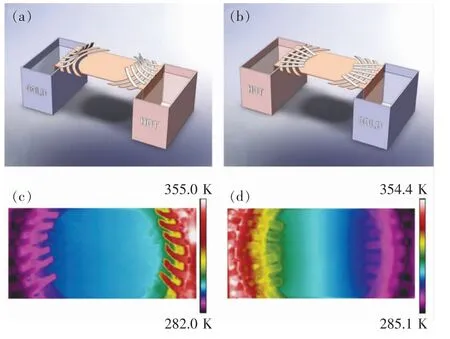
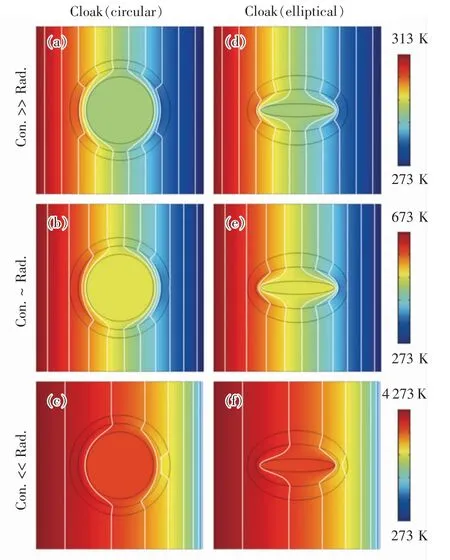
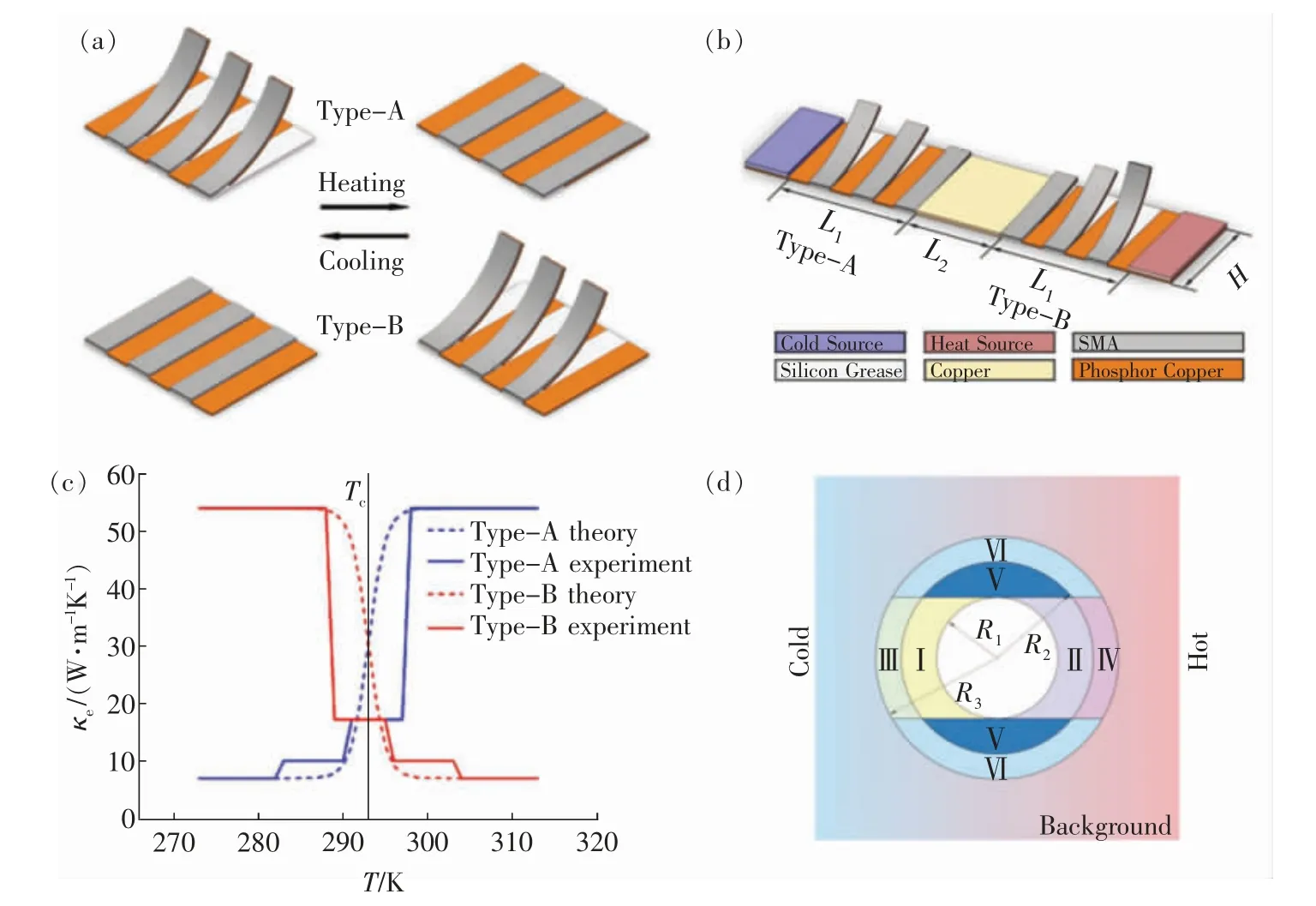
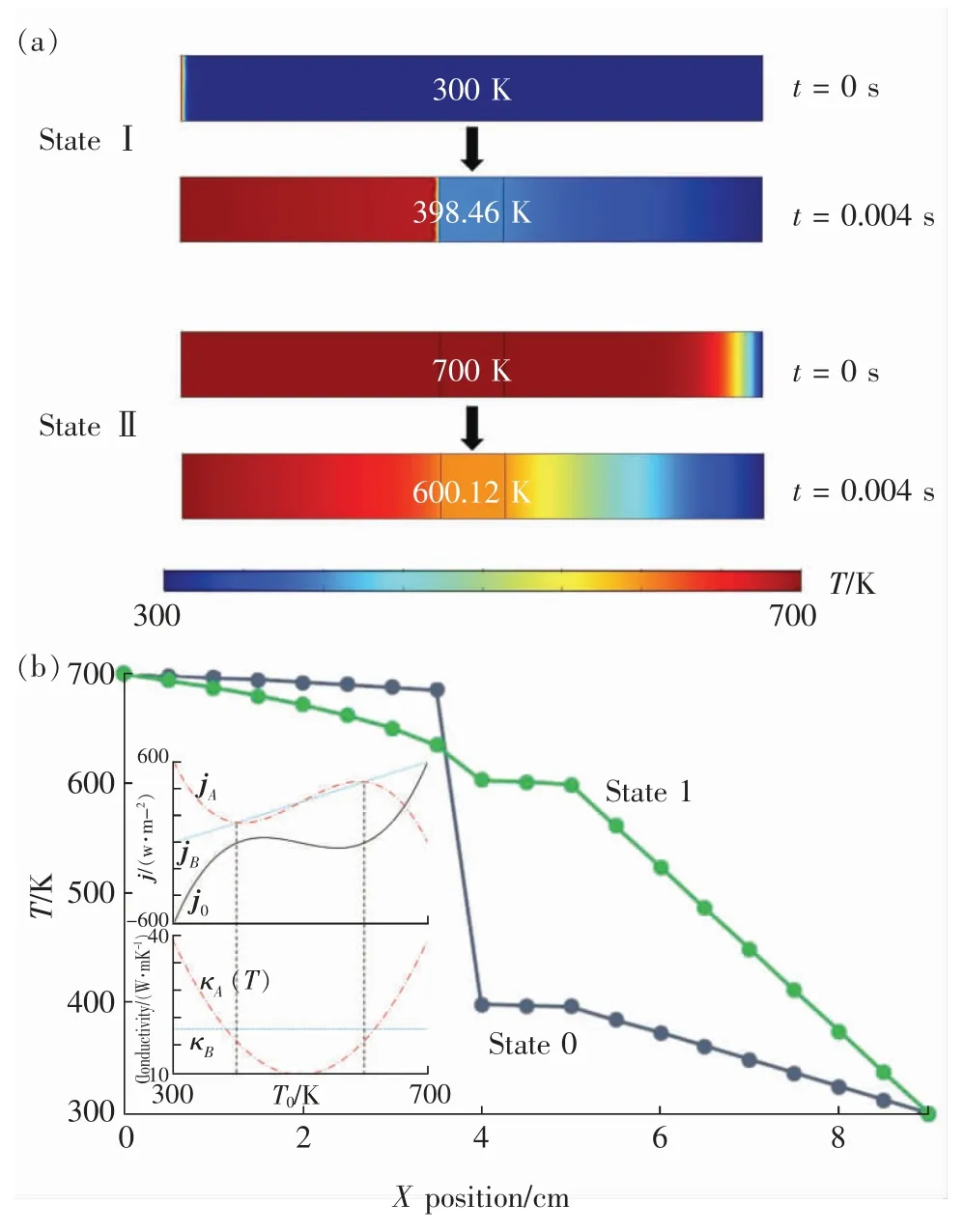
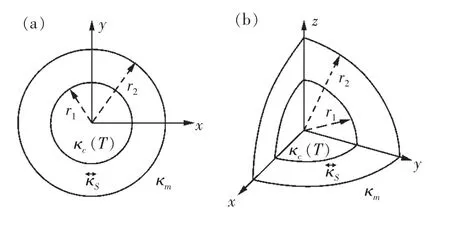
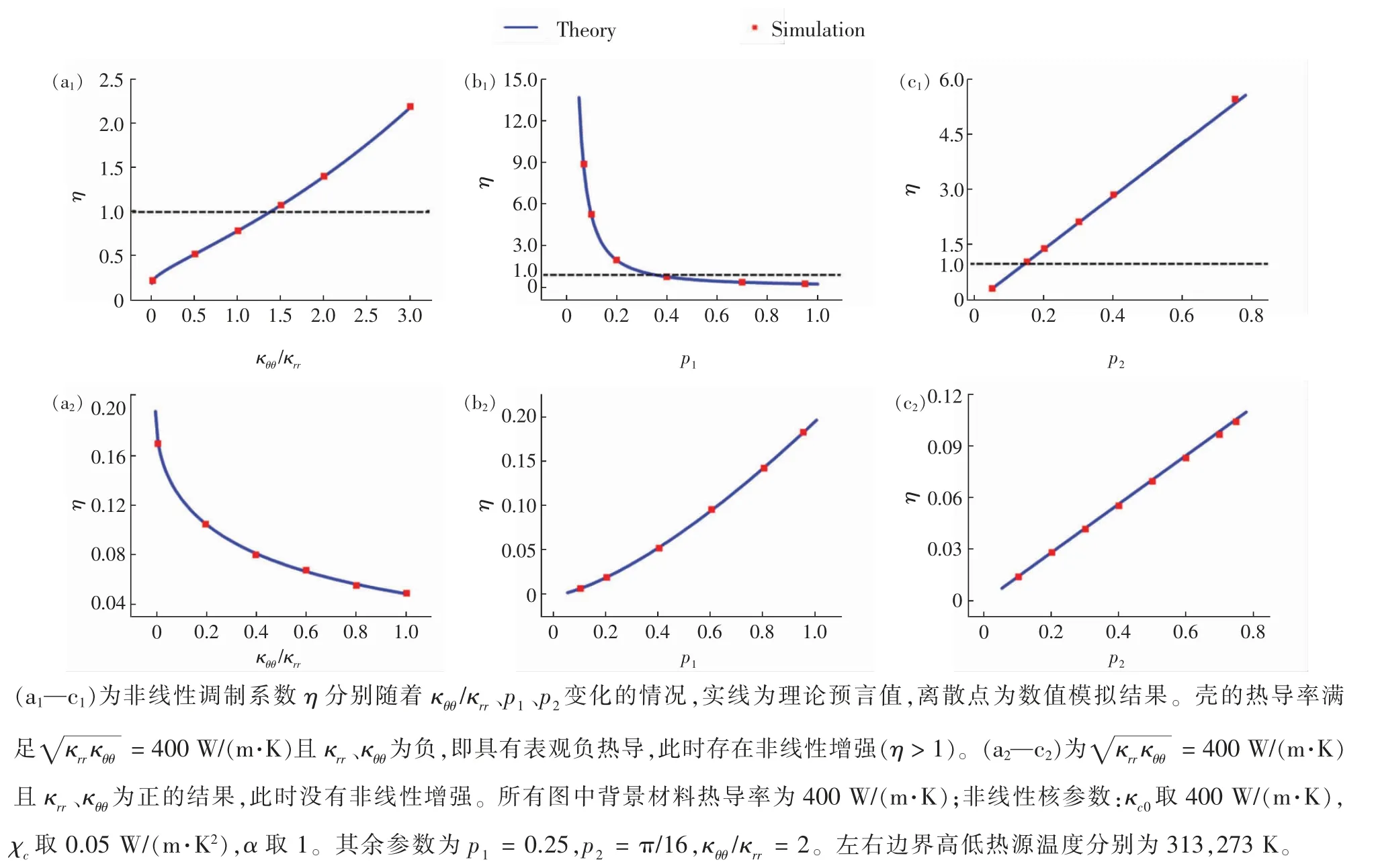
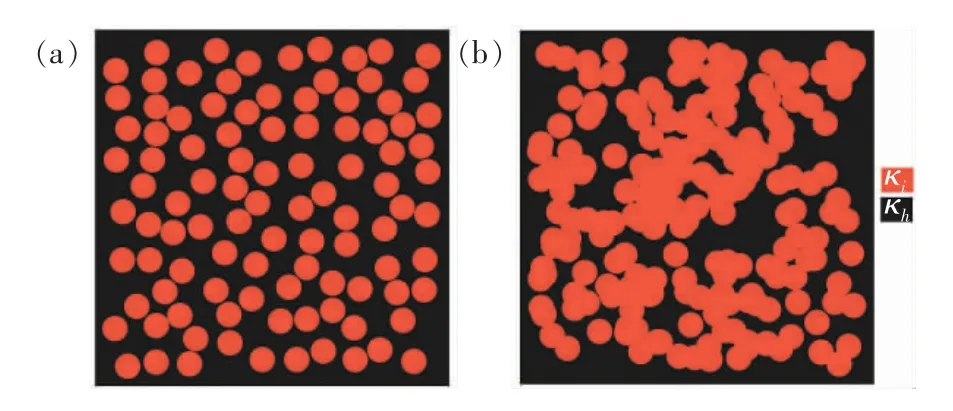
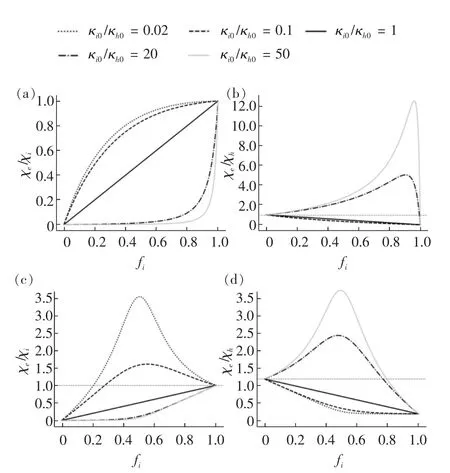
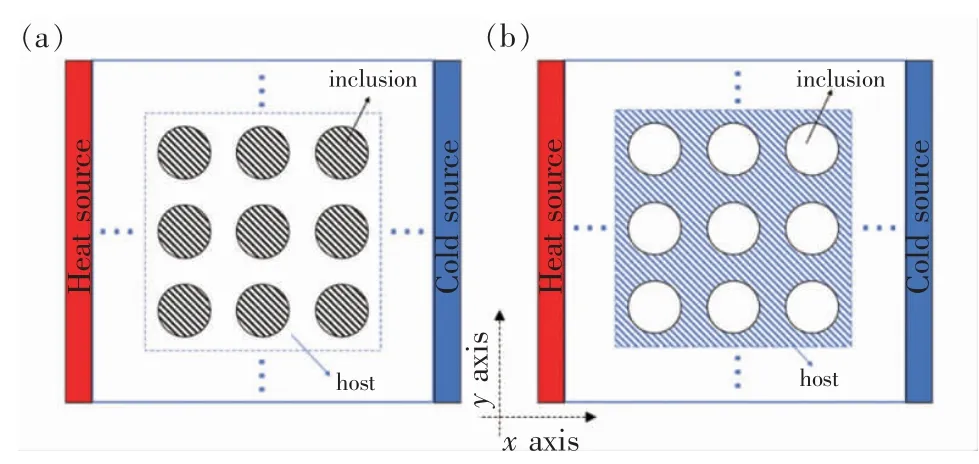
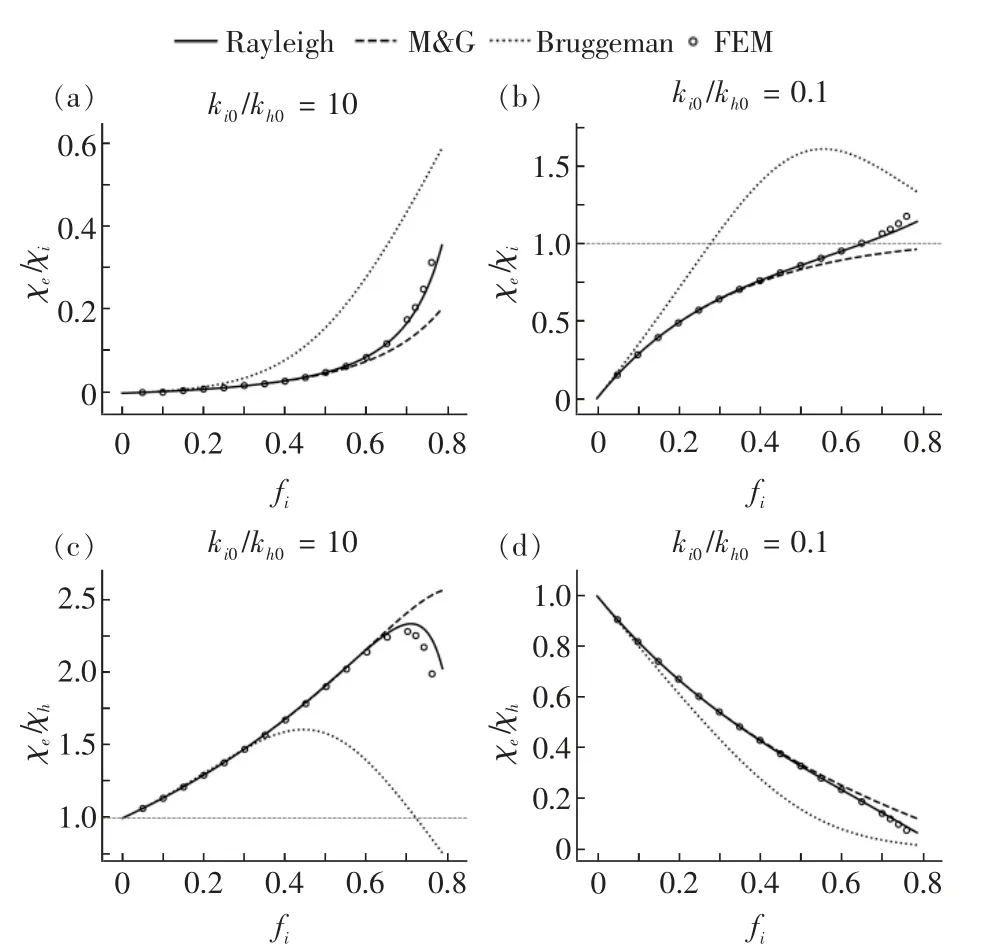
其中0 根据非线性变换热学理论,热隐身斗篷也可应用于背景为非线性导热材料的情形,此时热导率的变换规则形式上与线性导热的情形相同,只需要将κm理解成与温度相关的κm(T)。此后Xu 等基于远场热辐射中的Rosseland 扩散近似模型[42]建立了同时考虑传导与辐射的多热场变换理论[43],这是一种特殊的非线性变换热学理论,整个体系在数学形式上与傅里叶定律下的热传导相同,总热流j 为传导热流jcon=-kΔT 与辐射热流jrad=-γT3ΔT 之和。此时可以将κ+γT3理解成总的非线性热导率,其中κ是传导贡献的部分,γT3是辐射贡献的温度依赖的热导率。根据Rosseland 扩散近似模型,γ 是与材料折射率n 及Rosseland 平均消光系数β 有关的物理量(辐射热导率非线性系数),取值为γ=-16 σn2β-1/3,其中σ 是斯特藩-玻尔兹曼常数。此时隐身斗篷参数的传导热导率部分与线性传导时的变换规则相同,辐射部分(背景材料对应的非线性系数记为γm)参数为Xu 等人据此设计了多热场隐身斗篷,即同时屏蔽斗篷内障碍物的辐射、传导对斗篷外热信号的影响。如图2所示,根据传导热流jcon与辐射热流jrad占比的不同,他们取3 组不同的温度范围来进行瞬态模拟,这也可以理解成不同温度范围下热导率的线性部分与非线性部分贡献不同。从图2 中可以看出,随着时间变化,背景等温线保持笔直,这与整个区域为均匀材料的参照组的温度分布相一致,即实现了热隐身。 图2 基于Rosseland 辐射模型的多热场瞬态隐身斗篷数值模拟结果[43]Fig.2 Simulation results of a transient thermal cloak for conduction and Rosseland radiation model[43] 他们同时也设计了对应的热聚集器(热流在中心区域增强)与热旋转器(热流在中心区域旋转一定角度),并使用了两种均匀、各向同性材料组成的多层结构来实现所需的各向异性参数的效果。实际上将辐射的传热效果用等效热导率来表示是一种常见做法,比如衡量行星内部辐射[44-45]与气凝胶材料[46-47]在高温下的导热属性。这也说明热传导中非线性因素的引入也可靠其他传热机制来实现。 而为了实现线性导热材料所不具备的更灵活的调控功能,Li 等[39]利用强非线性导热材料设计了可开关的稳态热隐身斗篷,即只在一定温度范围内隐身效果打开。一种设计方法是对线性情形下的几何变换进行修正,Li 等人给出的参数为 图3 A 型可开关隐身斗篷的温度分布数值模拟结果[39]Fig.3 Simulation results of a type-A switchable thermal cloak[39] 此后,Shen 等[48]也根据非线性变换热学理论设计了可在隐身与聚集间切换功能的器件以及瞬态可开关的热聚集器[40](此时除了调制特定的热导率分布,还需要考虑材料密度与比热的设计)。这类器件可以根据环境温度决定是否工作或者根据不同温度实现不同功能,从而属于智能或主动热调控器件。 Li 等[39]从可开关热隐身斗篷的结构中得到启示,进一步设计了宏观热二极管。如图4(a—b),中间框内的区域为准一维的宏观热二极管结构,分为3 个区域,区域Ⅰ、Ⅱ、Ⅲ分别为A 型可开关隐身斗篷(高温工作)的部分结构、B 型可开关隐身斗篷(低温工作)的部分结构、热的良导体(如铜)。这个结构显然是非对称且强非线性的,区域Ⅰ、Ⅱ中的热导率总体上属于临界温度不同的Logistic 函数形式,从而可以预计有一定的整流作用,这也被数值模拟所证实。 他们也利用形状记忆合金(shape memory alloys,SMA)在实验上实现了这种宏观热二极管。形状记忆合金是一种特殊的相变材料,能够温度改变时发生形变,从而与其他介质接触或断开并影响传热效率。相变可以视为一种极端的非线性关系,并恰好满足Logistic 函数形式的热导率要求。如图4(c—d)与图5,实验样品中的隐身斗篷部分由铜与发泡聚苯乙烯交替组成隐身斗篷所需的弧形多层机构,并在上面放置条状的SMA(两侧的SMA 在被加热时的形变方向相反,区域Ⅰ内的SMA 在高温时向上翘起,而区域Ⅱ内的SMA 在低温时向上翘起),中间是铜板。交换冷热源使得SMA 从翘起(断路状态)变为与下方材料接触(导通状态),即实现了整流效果。2020 年Kasali 等[49]利用二氧化钒与聚乙烯(PE)两种相变材料设计的热二极管与Li 等设计的宏观热二极管具有相似的原理。二氧化钒可在340~345 K 的温度范围内发生金属-绝缘体相变,从而剧烈改变材料的热导率(随温度升高而升高)、光学吸收率、介电常数等性质,具有广泛的应用[50]。与之相似,聚乙烯的热导率在395~400 K 的温度范围内也发生急剧变化(随温度升高而降低),它与二氧化钒的热导率都可以用Logistic 型函数κH+来表示(κH为高温下的热导率,κL为低温下的热导率)。在250 K 的温差下,通过二氧化钒与聚乙烯相接触的两组分结构,他们实现了约60%的整流比。 图4 宏观热二极管[39]Fig.4 A macroscopic thermal diode[39] 图5 宏观热二极管实验结果[39]Fig.5 Experimental results of the macroscopic thermal diode[39] 散射相消理论[51]是超构材料领域常用的方法之一,在热超构材料中最初被应用于设计双层(bilayer)隐身斗篷[52-53],其中每一层材料都是均匀各向同性材料,从而避免了变换理论对隐身斗篷热导率各向异性的苛刻要求。散射相消理论可以一般理解成是根据所需要的物理场分布直接求解物理场控制方程的第一性原理方法,在宏观热传导中即求解傅里叶传热定律(均匀各向同性材料、稳态下即拉普拉斯方程)。下面介绍直接求解含有温度依赖热导率的傅里叶定律(即变热导系数问题)而设计的一些热调控器件。 将双层热隐身斗篷推广到非线性导热情形并不只是一个简单的类比,因为求解非线性热传导方程往往更为困难。Xu 等[54]基于Rosseland 扩散近似引入非线性的辐射热导率,直接求解传热方程Δ(κ+γT3)ΔT)=0(见1.1 节),设计了传导、辐射同时存在下的多热场双层隐身斗篷。通过类似基尔霍夫变换的方法,他们将传热方程化为某个温度相关标量的拉普拉斯方程,并根据解出的温度分布计算得到了一般的核-壳结构的总的等效热导率(等效热导率与平均温度梯度之积等于平均热流),从而根据热隐身的判定条件(等效热导率与背景相同)精确给出了双层斗篷中外层材料传导热导率κ 与辐射热导率系数γ(取折射率为1,则调制Rosseland平均消光系数β)的取值,此时斗篷的内层材料必须绝热即热导率为零。如图6 所示,他们设计了圆形与椭圆形结构的热隐身斗篷,并通过在左右两侧施加不同温度的热源做了3 组对应的模拟,使得传导(线性热导率部分)与辐射(非线性热导率部分)对热流的贡献占比不同的情形都得到了验证。由于数值模拟中无法出现零值热导率,斗篷内层的传导热导率κ 与Rosseland 平均消光系数的倒数都设置为相对背景材料取值的小量。 图6 传导、辐射多热场或非线性导热材料双层热隐身斗篷的温度分布数值模拟结果[54]Fig.6 Simulation results of bilayer cloaks for multithermotics/nonlinear conduction[54] 基于同样的方法,他们也设计了适用于多热场或非线性热传导的热透明(transparency)、热扩展器(expander)等器件,并讨论了计算得出的参数在瞬态传热下的适用情况。此后,Su 等人[55]将这一理论推广到更一般的对温度呈多项式关系的非线性热导率形式,并设计了可实现低温聚集、高温隐身的功能转换热调控器件。 如上文中提到,热隐身斗篷可以使得内部物体不会影响外部背景的温度分布;此外根据一般的认识,因为斗篷(一般为环形)内圈的径向(此时也为界面法向)热导率为零,斗篷也防止了热流进入内部物体。然而常规线性导热材料制备的热隐身斗篷内部的温度会随着环境温度的变化而变化,这意味着瞬态过程中必然有热流进入斗篷内部,因为无论是数值模拟还是实验,斗篷内圈的径向热导率都不可能取绝对的零值。举例来说,如果热隐身斗篷置于背景的中心,在背景左右两侧加上高低热源,温度分别为TH和TL,那么在整个系统达到稳态后,斗篷内部的温度将是(TH+TL)/2,而不是保留在初始值。如果要斗篷内部区域维持在某一特定温度,则必须要引入额外的能量来实现,一个实际的例子就是空调系统。这种有害的特征大大削弱了热隐身斗篷的实际应用价值。2016 年,基于非线性导热材料,Shen 等[56]设计了一种零能耗保温的器件,即无需外部能量的输入就可维持某一区域在特定温度上。 首先,他们提出了一种温度捕获(temperature trapping)理论,用一种准一维的三组分非对称结构来实现零能耗保温的目标。图7(a)中零能耗保温器件模型的左右两侧区域分别应用两种相变材料,称为Type-A(A 型)和Type-B(B 型)。这两种材料的相变温度相同,区别在于A 型材料在高温时是热的良导体,而在低温时是热的不良导体;B 型材料的相变方向正好与之相反。两种相变材料的热导率都满足Logistic 函数的形式,可以分别表示成其中ε 是小量而Ξ 很大。中间区域是一种热的良导体材料,该区域也是希望保温的区域。通过求解稳态非线性传热方程,Shen 等人证明了中间区域的温度只取决于A、B 材料的相变温度,不再受到环境温度(即左右两端施加的热源)的影响。在图7(e)中他们设计了一组对比模型,即将左右区域替换为常规的线性材料。有限元模拟的结果验证了温度捕获理论。在环境温度大幅变化的条件下,左边一列设计的模型中心区域几乎保持恒温,而右边一列参照组的中心温度随着环境温度而变化。 图7 温度捕获理论对应的零能耗保温器模型[56]Fig.7 Energy-free maintenance based on temperature trapping theory[56] 实验上,他们应用了此前在宏观热二极管实验中已经发挥过作用的两种类型的SMA 来制备多级双金属片结构(如图8(a—b)),实现了理论所要求的非线性热导率(如图8(c)),并且实验结果与理论预测的结果非常相近。基于温度捕获理论,Shen 等人进一步优化了双层热隐身斗篷,设计了恒温热隐身斗篷。与线性材料制备的双层热隐身斗篷不同的是,恒温热隐身斗篷内层分为Ⅰ、Ⅱ、Ⅴ3 个区域,外层分为Ⅲ、Ⅳ、Ⅵ3 个区域(如图8(d)),除了Ⅴ、Ⅵ两个区域使用线性材料外,其他区域都使用相变材料。4 种相变材料临界温度相同,且每一层中的两种相变材料在加热时趋于高低不同的导热状态。数值模拟结果显示这种结构的隐身斗篷中心区域的温度取决于相变温度。这种利用相变材料与非对称结构的保温器设计最近也被推广到同时考虑传导与辐射传热的体系中[57]。 图8 利用形状记忆合金设计的零能耗保温器及优化的隐身斗篷[56]Fig.8 Structure of the energy-free maintenance device based on SMA and its application on an optimized cloak[56] Wang 等[58]在以上工作的基础上,在零能耗保温系统中引入热电效应,实现了在零能耗保温的基础上对外发电的功能。图7(a)模型的中间良导体区域保温,环境(热源)温差产生的温度梯度将集中于左右两侧的非线性材料上,因此,当该材料具有热电效应时,它会将整个环境温差都用于形成热电势,即在保温的同时产生温差电动势,进而可以对外做功。此外,他们还提出了当热场与电场耦合时双层热电隐身衣的设计原理,给出了耦合场下隐身衣的制备参数要求。在这个双层热电隐身衣的基础上,通过给予整个系统某一均匀热电耦合系数(即赛贝克系数),在将内层材料替换为热参数和电参数的同时在某一临界温度发生相变的材料后(同样可通过SMA 实现),成功实现了中心恒温的热电隐身斗篷。该斗篷在中心区域恒温的基础上,具有对外发电的新功能,在节能建筑、汽车、飞行器等方面有潜在的应用价值。 双(多)稳是一种典型的非线性效应,即体系在相同的环境参数下能够具有两(多)个稳态,如人们熟知的磁滞效应,被广泛用于信息存储、开关、布尔运算的实现。2008 年,Wang 等[18]根据非线性的FK晶格及其负微分热阻效应在理论上实现了微纳尺度的热学双稳及热存储器的设计,并在2011 年由Xie 等[59]通过二氧化钒纳米束在相变时产生的热滞效应在实验上制备了热存储器及设计了施密特触发器。2020 年,Wang 等[60]提出了宏观热学双稳现象并设计了对应的热存储器件。他们仿照前人采用的准一维三组分结构,如图9(a)所示,该结构由A、B、C 3 部分组成,并在左右两端施加热源。C 区域设置为良导体,并且相对A、B 区域较窄。由于热导率较高,C 区域趋于一致的温度分布,净热流近似为零,可以作为读取温度的区域。此时双稳的目标被设定为C 区域在稳态时可以有两个不同的温度取值,为此A、B 区域的热导率必须至少有一个为非线性。通过A、B 区域内热流与C 区域温度之间关系的定性分析,Wang 等发现一种简单的参数选择即A 区域热导率与温度呈二次多项式关系而B 区域热导率与温度无关,并利用基尔霍夫变换求解非线性传热方程得出了A、B 区域的热导率,这也与另一种平均热流法得出的结论相一致。A 区域内的热导率可以一般表示为 图9 宏观热学双稳结构及其热流分析[60]Fig.9 Schematic graph of macroscopic thermal bistability and its heat flux analysis[60] 根据计算可以发现该关系式中的二次项系数χA2与一次项系数χA1符号相反,这也与双稳的产生需要两种作用相反的机制相竞争(这里阻碍与利于传热)这一基本原理相符合。 他们也用有限元数值模拟验证了理论得出的参数。如图10(a)所示,整个热学双稳器件长9 cm,宽1 cm,左右两侧非线性材料(A、B 区域)长4 cm,中间良导体材料(C 区域)长1 cm,左右高低温热源分别为700 K 与300 K。状态1(State I)中整个器件的初始温度设置为300 K,而在状态2(State II)中设置为700 K。模拟结果显示两个初始态在到达稳态(弛豫时间不超过0.004 s)时C 区域中心趋于不同的温度分布,当然整个器件的温度分布也不相同,即实现了热学双稳。C 区域中心的两个稳态温度可以分别代表信号0 与信号1。他们也用该器件模拟了热学信息(温度)存储的完整过程,见图10(b),包括初始化(输入300 K 的初始温度)、读取(趋于StateⅠ的稳态后读取C 区域中心温度)、写入(再次输入700 K 的初始温度)与读取(趋于StateⅡ的稳态后读取C 区域中心温度)。两个稳态之间的转变时间约为0.004 s,这依赖于材料的热扩散率。热导率对温度呈二次多项式关系的自然材料包括二氧化锆。Wang 等人也根据温度捕获理论设计了利用SMA 实现这项功能的多级金属片结构。 图10 宏观热学双稳及热存储过程数值模拟结果[60]Fig.10 Simulation results of macroscopic thermal bistability and memory[60] 在线性热传导框架内的热超材料设计中,使用各种结构的复合材料来匹配需要的热导率分布已经成为器件制备的重要手段,因此有效媒质理论(或有效媒质近似)[61]等预测复合材料等效物性尤其是等效热导率的方法也被经常使用。当非线性导热材料被纳入热超构材料的设计中,也必然要求提升预测非线性导热复合材料等效热导率的能力。下面介绍课题组针对不用的复合结构发展的非线性等效热导率的计算方法及部分应用。在2.1 节中也提到了核-壳结构非线性等效热导率的计算,其与下文内容的区别在于前者是一种完全基于控制方程的精确求解,而下文内容涉及的方法则属于(有效媒质)近似理论。 因其良好的对称性,核-壳结构可以说是热超构材料设计中最常用的结构,如线性导热材料制备的热隐身斗篷[32]、热变色龙[34]、热放大器[35]等。Yang等[62]考虑了具有非线性热导率的核-壳结构(如图11(a)),核的半径为r1,壳的半径为r2。核为非线性材料,壳及背景为线性材料。特别地,壳的热导率各向异性(记为二阶张量)且在二维情形下可用极坐标表示成对角的(κrr,κθθ)。他们考虑核的热导率κc为κc=κc0+χcTα,其中κc0为热导率的线性部分,χc为热导率的非线性系数。在非线性光学中,非线性极化系数的增强是一种重要现象[63]。Yang 等[62]考虑核中热导率的非线性部分远小于线性部分的情况,即弱非线性或微扰非线性,并将整个结构置于边长为a 的正方形区域的中心并在左右边界施加热源。此时核-壳结构的等效热导率κe可以通过级数展开截取成κe=κe0+χeTα,并根据对线性材料核-壳结构等效热导率的已知结果运用微扰法计算得到了核-壳结构的等效非线性系数。他们发现非线性增强(即非线性调制系数η≜χe/χc>1)需要壳中存在表观负热导率,这可以通过额外增加热源来实现,并得到有限元数值模拟的验证。图12 中展示了根据η 的表达式给出的理论预测与有限元数值模拟结果的对照,其中κm是背景材料热导率,且他们进一步将理论推广到三维情形(对应结构如图11(b)所示),并得到类似的结论。 图11 二维、三维核-壳结构示意图[62]Fig.11 Two/three-dimensiona core-shell structures[62] 图12 二维核-壳结构等效非线性系数增强的数值模拟结果[62]Fig.12 Simulation results of nonlinear coefficient enhancement in 2D core-shell structures[62] 无序或随机结构是另一种热超构材料中常用的结构,可被用来实现热伪装、热幻象[64-65]等功能。Dai 等[66-67]考虑无序非线性导热复合材料的两种基本情形。情形Ⅰ中非线性颗粒(热导率κi=κi0+(T+Trt)α)嵌入线性基底(热导率κh=κh0);情形Ⅱ中线性颗粒(热导率κi=κi0)嵌入非线性基底(热导率κh=κh0+χh(T+Trt)α),其中Trt是一个不影响最终计算结果的参考温度。如果用计算机辅助生成随机结构,则需要考虑嵌入颗粒(一般选择为圆形)在依次投入基底中时是否交叠,见图13。如果可以交叠,则最终产生的结构具有一定的对称性,即嵌入颗粒与基底材料不可区分。 图13 无序结构复合材料示意图[67]Fig.13 Composite with disordered structures[67] 有效媒质理论中M&G 公式[68]与Bruggeman 公式[69]可分别处理非对称(不可交叠)与对称(可交叠)这两种情况。类似于核-壳结构中的处理方法,Dai等[66-67]将非线性热导率代入有效媒质理论,根据微扰法得出了等效热导率κe=κe0+χe(T+Trt)α的值,其中等效线性部分κe0由线性材料的M&G 公式或Bruggeman 公式给出。具体而言,对于情形Ⅰ,M&G 公式(颗粒不可交叠)给出 易知Bruggeman 公式对应的两个结果在交换参数下标i 与h 后变为对方,即对称。图14 中给出了参数κi0/κh0不同取值下,非线性调制系数χe/χi或χe/χh随嵌入颗粒面积分数fi变化的情况,可以看出由于对称性,两种情形下颗粒可交叠的结构都能产生非线性增强,而颗粒不可交叠的结构只能在线性颗粒嵌入非线性基底时发生。Dai 等[66]也给出了部分结构的数值模拟结果。 图14 无序结构复合材料中的非线性增强效应[67]Fig.14 Nonlinear enhancement in disordered composites[67] 周期结构是各类人工晶体材料的基础,也在热超构材料中被用于设计热透明、热幻象等器件[70-71]。计算周期结构复合材料等效物理属性的典型方法是基于Rayleigh 恒等式的Rayleigh 方法[72],在光学或电学中即直接求解周期性系数的拉普拉斯方程,并通过数值方法确定等效物理属性的最终表达式,是一种半解析的第一性原理方法。在非线性光学中,Gu 等[73]也发展了对应于弱非线性电导率的非线性Rayleigh 恒等式,并通过微扰法计算电学高阶小量的控制方程,最终得到等效电导率关于电场的非线性系数。因为线性热传导与线性导电方程具有相同的形式,可以预期Rayleigh 方法也适用于线性热传导并给出与等效电导率相似形式的等效热导率。然而,由于热导率对温度(势)的依赖关系与电导率对电场(势的梯度)的依赖关系有着根本的区别,使得在非线性热传导中使用微扰法求解高阶小量方程十分困难。 Dai 等[74]则转而直接从求出的线性等效热导率出发,沿用核-壳结构与无序结构中使用的对温度的级数展开与截断高阶量的另一种微扰方法得到了热导率的等效非线性系数。他们依然考虑对情形Ⅰ即非线性颗粒嵌入线性基底与情形Ⅱ即线性颗粒嵌入非线性基底,如图15 所示,且颗粒结构为圆形,并采用四方晶格。在Rayleigh 方法中颗粒的形状及晶格构型对最后的计算结果有一定影响。相应的非线性调制系数分别为 图15 周期结构非线性复合材料示意图[74]Fig.15 Nonlinear composite with periodic structures[74] 这里ζ=3.312 48。由于Rayleigh 恒等式考虑了周期性颗粒间的多极矩相互作用,使得在颗粒面积分数较大时比有效媒质理论更为精确,这也可以从图16 中理论预测与数值模拟结果的对照中看出。同时可以发现,周期结构中无论是非线性颗粒嵌入线性基底还是线性颗粒嵌入非线性基底的情形,都有可能发生非线性增强效应,前提是参数κi0/κh0满足一定条件。对于前者即情形Ⅰ,κi0/κh0需要足够小,临界值约为1/3.5;对于后者即情形Ⅱ,κi0/κh0需要足够大,临界值约为2.5[67]。Dai 与Huang[74]也考虑了强非线性的情形,给出了基底材料与嵌入颗粒的热导率为温度的相同幂次关系时,基于Rayleigh 方法或有效媒质理论的等效热导率与等效非线性系数的解析表达式。 图16 周期结构复合材料中的非线性增强效应[74]Fig.16 Simulation results of nonlinear enhancement in periodic composites[74] 本文介绍了近年来利用宏观尺寸的非线性导热(热导率直接或间接对温度具有响应的)材料进行热超构材料与热调控器件设计的理论研究与实验方面的进展,并希望以此为基础推动“非线性热学”这一学科的发展。可以看到,不仅以往基于线性导热材料制备超构材料的方法可以扩展到非线性热传导上并实现相似的热调控功能,而且新的功能器件尤其是具有根据环境参数实现不同功能的智能调控器件能够通过非线性导热材料制备。限于篇幅与文章框架,上文中我们主要探讨的是傅里叶传导定律下的传热,下面我们就更一般的热学中的非线性现象分3 个方面进行补充、讨论及展望: 1)宏观与微观 区别于以非线性晶格中声子能谱理论为基础的微观层面的工作,课题组的相关工作可以归入宏观唯象理论的范畴。而在声子理论之外,研究者们也基于电子[75-76](传导)、光子[77-79](辐射)的传热机制在微观层面展开热学中非线性效应的研究。这里可以对应非线性光学做一个类比。基于具有非线性热导率的材料研究对应于非线性光学中的非线性极化理论,即非线性光学中半经典框架下的传统内容,而基于声子等载流子的微观理论可以对应于全量子理论的非线性光子学[80]。有趣的是,与非线性光学的发展历程相反,直接利用非线性材料(主要指体材料)的热学研究受到重视反而更晚,这也启示可以在唯象理论方面继续进行更深入的工作。同时,如何在微观与宏观间建立联系而不是完全割裂也值得思考,这有助于相关理论与器件设计适用于更大的范围,如部分工作以非线性晶格构造所需体材料的温度响应热导率[23,25],又比如对热导率呈幂次关系的热导率及傅里叶定律也可以适用于部分微纳系统[81]。 2)多热场与多物理场 前文中提到辐射本身在一些情形下可以等效为傅里叶定律下的非线性热导率[42-47]。对流也很早就被应用到热整流的设计中,比如受重力与密度差驱动的自然对流具有一定的方向性,从而造成交换冷热源时热流的差异[8]。近来,如何通过受迫对流产生Lorentz 非互易及热整流也被广泛研究[82-83]。辐射与对流能够带来非线性效应也启示我们其他物理场也可以有类似作用,这在微观或介观层面特别是量子系统中热电效应相关的非线性现象已经引起研究者的重视[84]。结合传热与其他物理领域的超构材料来实现非线性热输运也是一个有意思的话题,比如利用力学超构材料中Kirigami 折纸技艺产生的非对称受热形变来设计热二极管[85]与热开关[86]。 3)热波 一些非线性效应的产生要求具有极强的非线性,如双稳、开关器件等。而在波动系统如光学中,倍频、差频等现象的产生只要求具有非线性极化率即可。傅里叶定律下的热传导是典型的扩散系统,目前功能器件中利用的非线性效应也都依赖强非线性。将热波纳入“非线性热学”的研究对象无疑会丰富“非线性热学”的研究内容,比如很小(微扰)的非线性热导率也能产生高次热谐波[65]。虽然针对热波的研究可谓历史悠久[87],并且热波也已被纳入热超构材料的理论研究范围[88-89],但由于行波形式的温度分布在傅里叶定律框架内会迅速衰减,所以现实中完成热波相关的调控功能还十分困难。近年来研究人员开始关注唯象的对流-传导体系中具有波动形式的温度分布下的传热效应[90-93],例如与奇异点(exceptional point)相关的热输运[90-92]和热波晶体[93]等,而将波动与热学及非线性效应有效结合起来还需要在这些方面有更深入的进展。
1.2 可开关智能器件
1.3 宏观热二极管
2 非线性散射相消理论
2.1 双层隐身斗篷
2.2 温度捕获理论

2.3 宏观热学双稳

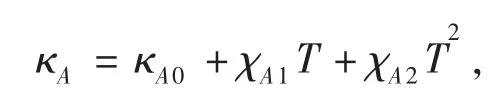
3 非线性导热复合材料的热导率计算
3.1 核-壳结构
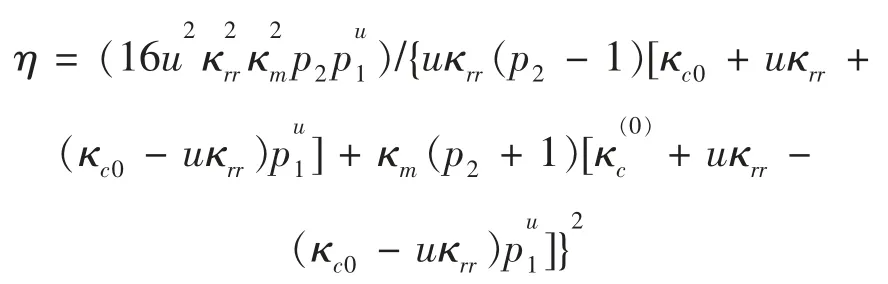
3.2 无序结构
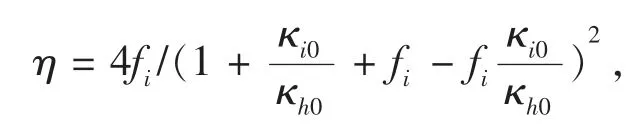

3.3 周期结构
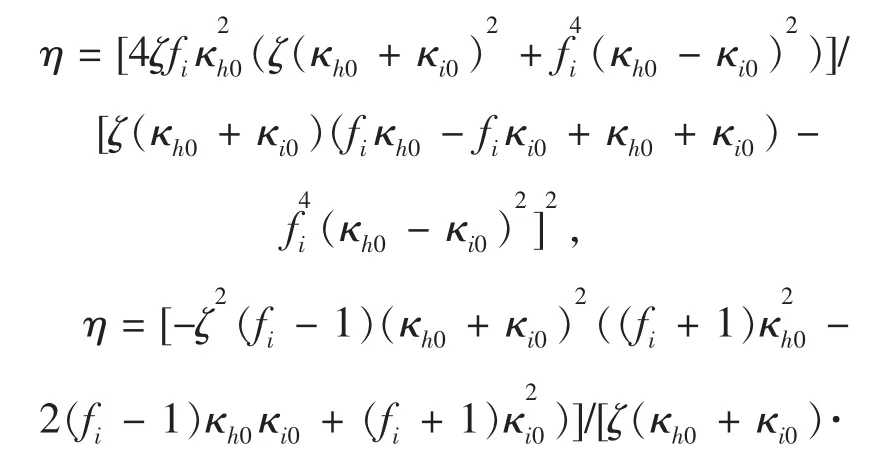

4 总结与展望

