基于3次B样条曲线的快速直接插补技术研究

李传军 张世辉 谢久明 韩晓方 程嘉强

(①天津中德应用技术大学机械工程学院，天津 300350；②天津华大科技有限公司，天津 300350)

在复杂曲面数控加工中，通常使用CAD/CAM软件将复杂曲面离散为微小的直线段或圆弧段，然后使用直线插补或圆弧插补完成复杂的加工，这种加工方式使得刀具轨迹不平滑，在微段连接处切向不连续，极大地降低了加工效率和表面质量。为了解决这个问题，样条曲线直接插补技术应运而生。

3次B样条是应用最广泛的样条曲线[2-5]， 目前已有多种不同的3次B样条曲线插补方法，如最早的泰勒一阶和二阶展开方法、反馈插补法、“预估——校正”插补法和函数拟合插补法[6-22]等，在这些插补方法中涉及多次曲线求值和求导计算，甚至需要进行反复迭代计算。而由于B样条基函数采用递归定义，其求值和求导过程十分复杂耗时，因此上述方法需要占用大量的计算资源，甚至影响系统的实时性。

针对刀具轨迹曲线的B样条曲线模型，本文提出从直接插补算法原理以及B样条曲线的数学模型出发，为了提高插补过程中的计算效率和计算精度，利用一种B样条的节点插入技术与微分递推求值进行3次B样条曲线的快速求值求导算法，整个插补实现过程不涉及任何B样条基函数的求值求导计算。解决了目前传统插补器无法有效插补该类型轨迹的问题，给出了插补点的计算过程和实现方法流程，利用仿真和开放式数控系统加工验证了此方法的效率和实时性。

1 3次B样条曲线快速直接插补

1.1 B样条曲线

B样条基函数是构造B样条曲线的基础，根据de Boor-Cox的递推定义，B样条基函数的递推公式为[1]：

(1)

式中：u为曲线参数；p为B样条基函数的次数；U=[u0,u1, … ,um]为非递减节点序列；Ni,p(u)表示序号为i的p次B样条基函数在参数u处的值，且规定0/0=0。

在B样条基函数的基础上，B样条曲线被提出。p次B样条曲线Q(u)的定义为[1]：

(2)

式中：Ni,p(u) (i=0,1,…,n)是定义在节点序列U=[u0,u1, … ,um]上的p次B样条基函数；Pi(i=0,1,…,n)为B样条曲线的控制顶点序列，顺序连接形成B样条曲线的控制多边形；B样条曲线次数p、控制顶点数量(n+1)和节点数量(m+1)之间满足：

m=n+p+1

(3)

1.2 连续3次贝奇尔曲线

利用3次B样条曲线的所有节点矢量和所有控制顶点，分别构成节点矢量集合U和控制顶点集合P，若节点矢量U中的某个节点ui满足ui=ui+1=ui+r-1，即连续r个节点值相等，则称ui中的重复度为r。采用样条节点插入技术，对U中的每次节点进行重复插入操作，直到每个节点的重复度均为3，此时3次B样条曲线转换为连续3次贝奇尔曲线，即每两个重复度为3的节点之间为一条3次贝奇尔曲线。通过B样条节点插入技术可以获得3次贝奇尔曲线的控制顶点。

1.3 快速直接插补模型建立

从新获取的任一段3次贝奇尔曲线，得到4个控制项点Q0、Q1、Q2、Q3，取1个偏移矢量V，将4个控制顶点Q0、Q1、Q2和Q3沿矢量V偏移后得到新的4个控制顶点P0、P1、P2和P3，使得P0、P1、P2和P3的坐标分量均不为0，令新的4个控制顶点分别为：P0=(x0,y0,z0)T,P1=(x1,y1,z1)T,P2=(x2,y2,z2)T,P3=(x3,y3,z3)T，则新的尔曲线可表示为：

(4)

式中：t为曲线参数；Bi,3(t)为3次伯恩斯坦基函数，计算为：

其中：符号“！”表示阶乘运算。

将式(4)变形为：

(5)

对式(5)两边计算关于参数t的一阶导矢可得：

(6)

其中：

ΔPi=Pi+1-Pi,i=0,1,2。

联立式(5)和式(6)可得：

C′(t)=MC(t)

式中：M为系数矩阵，表示为：

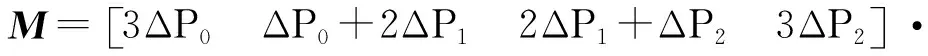
1.4 快速曲线直接插补

令C0=(x0,y0,z0, 1)T和t0=0，则第(i+1)个周期的插补点Ci+1计算为：

式中：Δti、k1、k2、k3、k4为插补点递推参数，计算为：

整个插补过程按照连续的每段3次贝奇尔曲线进行，当ti≥ 1时，所有贝奇尔曲线完成插补至终点。

2 仿真分析

2.1 五角形的3次B样条曲线快速直接插补算法

根据第基于3次B样条曲线快速直接插补算法其实现流程如图1所示。以图2所示的五角形的3次B样条曲线为例进行说明。

首先是获取3次B样条曲线的参数。获取3次B样条曲线的节点矢量U和控制顶点P，其中U={0, 0, 0, 0, 0.125, 0.25, 0.375, 0.5, 0.625, 0.75, 0.875, 1, 1, 1, 1},P={(60,90,0),(37.5,60,0),(0,60,0),(30,30,0),(22.5,0,0),(60,22.5,0),(97.5,0,0),(90,30,0),(120,60,0),(82.5,60,0),(60,90,0)}。

其次是将3次B样条曲线转换为连续3次贝奇尔曲线。通过B样条节点插入技术可以获得每段3次贝奇尔曲线的控制顶点。根据以上过程，获得8个贝奇尔曲线段，Q0、Q1、Q2、Q3每段3次贝奇尔曲线的控制顶点，各个贝奇尔曲线段的控制顶点如表1所示。

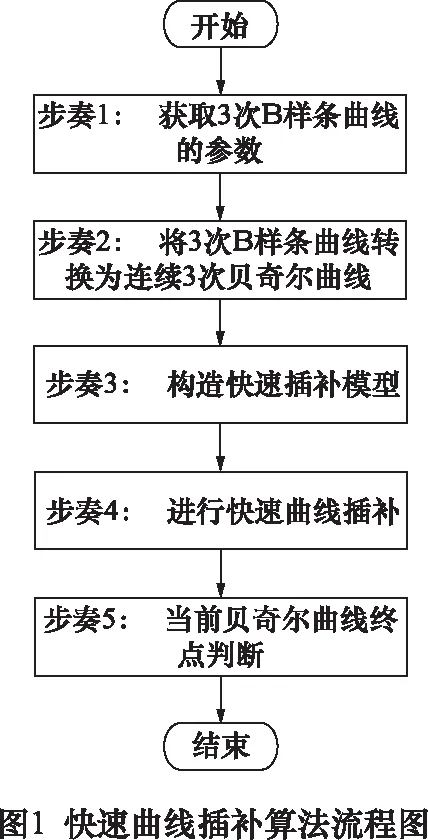
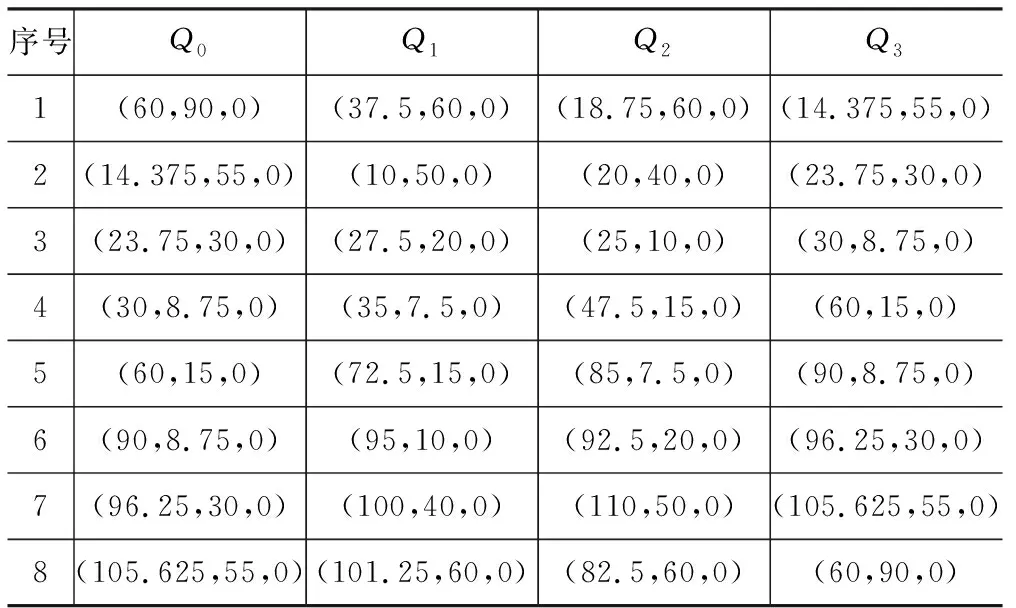
表1 贝奇尔曲线段的控制顶点坐标

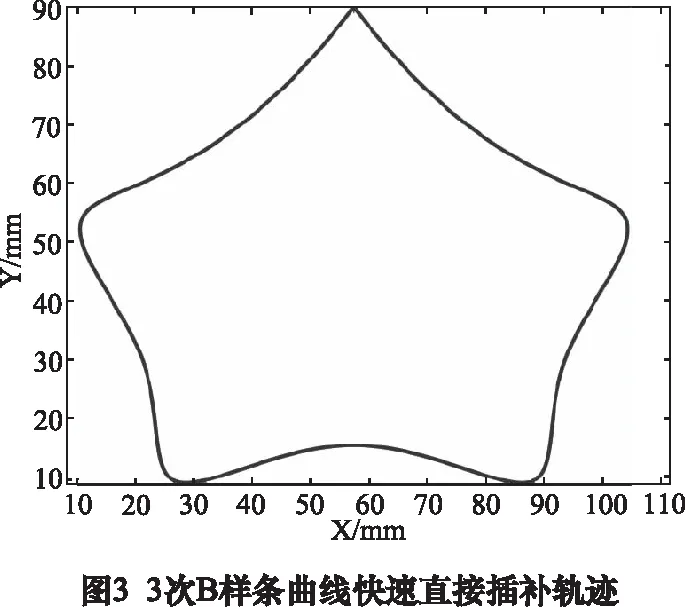
最后是完成快速曲线直接插补过程。由于所有贝奇尔曲线控制顶点的Z值均为0，因此选取偏移矢量V=(0,0,1)，得到所有的M为如表2所示。根据递推过程和贝奇尔曲线的终点判断，完成插补轨迹如图3所示。

2.2 插补效率分析

图4表示的是插补过程的速度波动，最大值小于0.015%。由于3次B样条曲线快速直接插补算法过程不涉及任何B样条基函数的求值求导计算，仅涉及矩阵乘法(可化为少量的四则运算)和四则运算，因此插补过程计算高效，且插补过程速度波动较低，同样具有较高的插补精度。

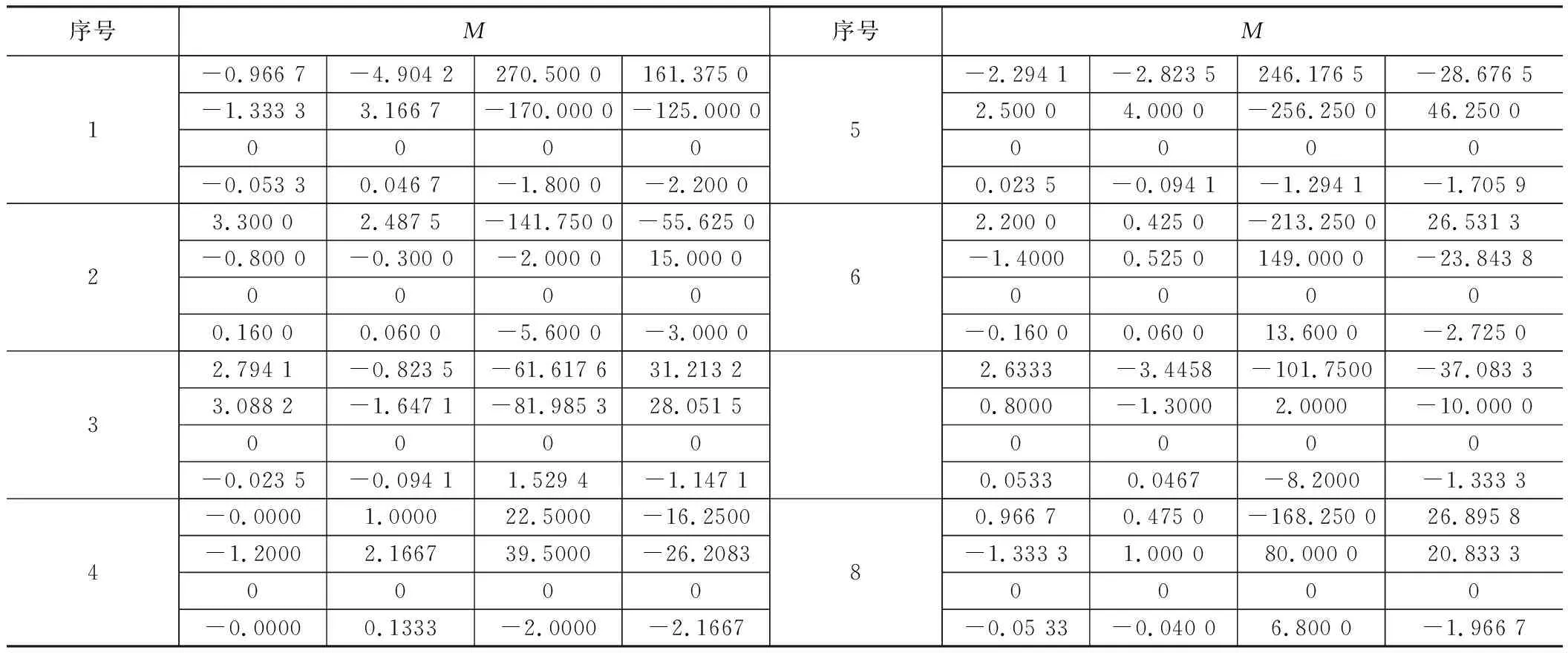
表2 3次B样条曲线快速直接插补系数矩阵

文献[1]给出了使用直接计算B样条基函数的方法来计算B样条曲线的各阶导矢的算法，并广泛应用于众多文献和软件应用。为了验证3次B样条曲线快速直接插补算法的计算效率，以文献[1]中的B样条基函数算法为对比，选取某B样条曲线为对象，分别用3次B样条曲线快速直接插补算法与文献[1]中的算法对相同曲线参数处的各阶导矢进行2000次运算，并获得CPU消耗的计时器周期数。仿真程序采用C#编写，仿真平台的CPU为Intel(R) Core(TM)i7-8550U CPU @ 1.99GHz，仿真结果如表3所示。

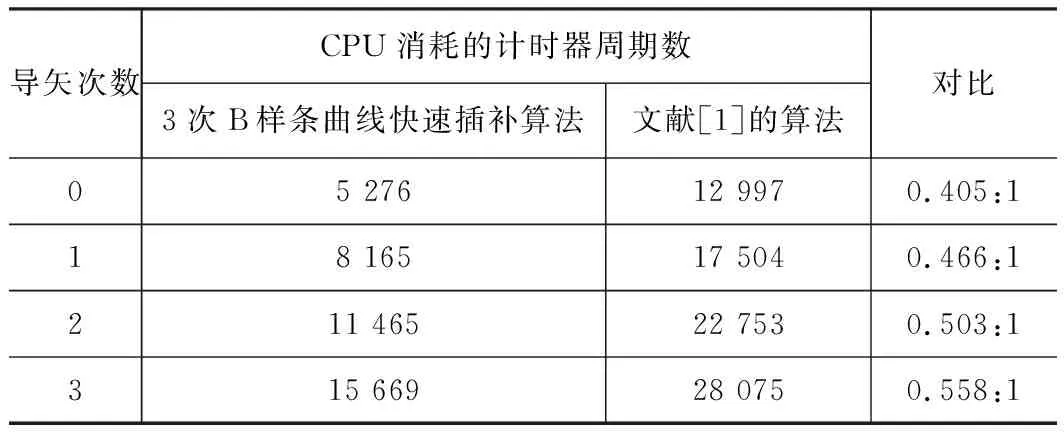
表3 两种算法计算时间对比

在插补过程中一般需计算曲线的前三阶导矢，因此表3列出了对3次B样条曲线求0至3阶导矢时两种插补算法使用的计时器周期数。从表中可以看出，本文提出的3次B样条曲线快速插补算法在求取0～3阶导矢时所用的时间大约为文献[1]中算法所用时间的50%。因此本文提出的快速插补算法能节省大约50%的计算时间，这在工程应用中对于提高B样条曲线实时插补计算效率具有重要意义。

3 加工验证

为了验证本文提出的3次B样条曲线快速直接插补的可行性，笔者所在项目组以TwinCAT技术为平台开发了国产三轴数控加工中心XK7132A为基础的开放式数控机床。分别以平面螺线和飞镖的B样条曲线为加工对象[23-27]，实际加工的机床以及结果如图5所示。

图5的加工过程表明，本文提出的插补方法成功应用于课题组开发的数控机床，并完成了平面螺线和飞镖的加工，因此3次B样条曲线快速直接插补算法是有效可行的。

4 结语

(1)提出了基于3次B样条曲线的快速直接插补算法，采用B样条节点插入技术将原始3次B样条曲线转换为连续多段的3次贝奇尔曲线，利用构造的快速插补模型，遍历每一段3次贝奇尔曲线，直到所有的3次贝奇尔曲线均快速插补完毕。

(2)提出了并进行了插补仿真分析对比验证，其插补计算高效，应用于数控系统其实时性得到提高。

(3)基于自主开发的数控平台上完成了平面螺线和飞镖的B样条曲线直接插补加工。