风力发电机主轴轴承等效寿命模型相似准则研究
金 晟 陈 捷 谷 然
(①南京工业大学机械与动力工程学院,江苏 南京122816;
风力发电机主轴轴承是风力发电机不可缺失的关键部件,其可靠性直接影响风力发电机的运行状况。有学者[1]都指出,轴承是风电机组中的薄弱环节,在实际工作过程中失效率高于其他风机部件。风电主轴轴承从工作寿命要求上说一般要求主轴轴承无故障运转13万小时以上,并且保证可靠度在95%以上[2]。而对主轴轴承进行寿命试验对于主轴轴承产品设计、主轴轴承健康检测、主轴轴承延长寿命都具有重要的研究意义。
根据我国现行国家标准文件GB/T 29718-2013[3],风力发电机主轴轴承按照布置结构形式的不同会有多种结构类型,但都属于滚动轴承范畴。目前,有很多学者对滚动轴承进行模型相似理论研究。润滑性能方面,陈志澜[4-5]等学者为研究三峡水轮机组推力轴承的润滑性能利用了模型试验并运用量纲分析法进行模型相似的推导。动力学研究方面,杨丕珠[6]等学者采用量纲分析的方法推导出变桨轴承的静力学及动力学相似准则;Desavale等[7]为研究调心滚子轴承动态响应的预测和设计方程,利用白金汉∏定理计算了33个相似准则;Kalpakidis[8]针对铅橡胶轴承防震动问题,使用了等比例缩小的模型并降低运动速度的条件下进行试验; Jamadar等[9]使用量纲分析矩阵法建立模型相似准则,结合响应面法(RSM)研究了缺陷尺寸、不平衡量、转速等因素对轴承振动特性的影响,并且提出使用量纲分析矩阵法对轴承的局部表面缺陷进行评估[10],金立兵等[11]研究了轴承中转子的振动特性诊断问题,利用无量纲参数建立了转子轴承系统的等效模型。上述研究都还未能将模型相似理论应用于轴承的寿命试验中。文献[12-13]则是基于模型相似理论的寿命试验方法在其他对象上的应用。
目前我国国内尚无一家企业已研发4MW功率以上风电轴承试验台。所以当前针对大功率的风力发电机主轴轴承原型进行全寿命试验并不现实。为了科学合理的验证其可靠性性能,使用尺寸缩小模型进行风电主轴轴承寿命试验是一种可行的方法。
本文使用量纲分析法基于现行轴承寿命模型理论考虑寿命影响因素和试验工况各物理量推导出风电主轴轴承等效寿命相似准则。通过相似准则可以得到风电主轴轴承模型在模型寿命试验应当实际加载的工况,并可以将模型寿命试验数据直接推广到原轴承模型。
1 相似理论及其应用方法
在实际工程运用中,相似准则相等是联系模型试验数据和实际对象数据的关键。在求解相似准则的过程中,主要有定律分析法、方程分析法和量纲分析法[14]。其中,定律分析法需要详细的物理学定律,并能判断出各个定律间的相互制约关系,实际解决问题中稍有不便。方程分析法则由于数理方程运算上的困难,在研究现象尚未透彻时,近似解只能在一定条件下求出[14]。而量纲分析法可以研究不局限于带有方程的物理现象,广泛应用于工程应用中。因此本文使用量纲分析法求解等效寿命相似准则。
图1是应用量纲分析法求解相似准则并提供验证的流程图。首先对风力发电机主轴轴承疲劳寿命问题进行分析,列出影响疲劳寿命的所有物理量参数以及试验条件参数;接着确定疲劳寿命问题的基本量纲以及对应数量的核心物理量;再依据相似第二定理建立其余物理量的相似准则;最后通过仿真的手段证明相似准则的准确性,为后续风电主轴轴承模型寿命试验提供理论基础。
2 主轴轴承等效寿命模型相似准则推导
2.1 风力发电机主轴轴承寿命理论
如图2所示,风力发电机主轴轴承按照类型主要可以分为调心滚子轴承、圆柱滚子轴承、双列圆锥滚子轴承和三排圆柱滚子轴承,都属于线接触向心滚动轴承范畴[4]。


最早将滚动轴承寿命形成系统理论的学者是Lundberg和Palmgren[15],其提出的轴承寿命理论被称为L-P理论。
1985年,Ioannides和Harris[16]对L-P理论进行了补充形成I-H理论。I-H理论考虑了疲劳极限应力并且放弃L-P理论中次表面最大正交剪切应力等常量,而代之假设轴承中材料的基本体积的生存概率,并用积分形式对所在深度进行表达。
Jalalahmadi[17]等人指出I-H理论的轴承寿命模型应由式(1)表示。
(1)
式中:a1是基于可靠性的修正参数,用来计算不同失效率下的寿命。a23是基于材料、运转温度、制造精度等的修正参数。
1992-1996年,Tallian[18-22]整合了国际上轴承试验的结果,在计算轴承寿命时同时考虑冶炼工艺、温度、材料、粗糙度、环境洁净度、表面缺陷等诸多因素,形成T理论。T理论是现行ISO 281-2007[23]标准的理论基础。根据何培瑜[24]学者对ISO 281-2007标准文件公式的推导,线接触滚动轴承的寿命公式经过修正后可表达为式(2)。
(2)
式中:a1是基于可靠性的修正参数,用来换算不同失效率的寿命,对寿命没有影响;aISO是考虑润滑和污染物的综合寿命卸载因子,根据标准文件[23],aISO可见式(3),由滚子个数Z、接触角α、滚子直径Dw和油膜参数Λ有关;C是轴承的额定动载荷值,是由Lundberg等人为代替上文L-P理论的来计算疲劳寿命所提出的近似方法的概念;P为施加的当量径向载荷;HRC为滚道表面硬度。
(3)
式中:x1、x2、e1、e2、e3、e4为无量纲修正系数;ec为污染系数,由污染物的类型、尺寸大小、数量、硬度决定;Cu为疲劳载荷极限,由轴承本身几何尺寸、接触角、滚子个数决定;Pa为轴承当量动载荷值;κ为反应轴承润滑条件的参数,主要由油膜厚度比Λ来反应。
2016年,徐鹤琴等[25]对滚动轴承疲劳寿命的影响因素进行了总结,研究了可靠度、温度、润滑剂和添加剂、表面粗糙度、材料、载荷分布、环向应力和界面滑动对滚动轴承疲劳寿命的影响。
本文依据上述成熟的国际标准轴承寿命理论为依据,对滚轴轴承寿命的影响因素进行总结。
2.2 物理量及其量纲
根据上文对风力发电机主轴轴承寿命的影响因素的总结,从材料上需要考虑的物理量主要有轴承材料的弹性模量、材料密度、材料泊松比、材料导热率、材料表面粗糙度和材料表面洛氏硬度;从轴承几何尺寸上考虑需要考虑轴承节圆直径、轴承接触角、轴承滚子直径、轴承滚子有效长度、油膜厚度、轴承滚子个数和接触角。为减少物理量个数,依据相似第一定理,当模型与原型满足相似时,几何尺寸必定相似,因此将主轴轴承模型形状几何物理量统一分为几何尺寸(包含表面粗糙度、油膜厚度等)、滚子数量和接触角。
参考我国滚动轴承试验标准文件[26]选择试验中各试验条件参数选择物理量为试验施加力、试验施加倾覆力矩、试验轴承转速和试验轴承温度梯度。
试验数据后处理不影响轴承寿命,但是为方便轴承寿命数据后处理分析还需要考虑这些物理量[26]:失效率、轴承寿命(转数)、寿命试验进行时间以及轴承表面剥落面积(用以判定轴承失效条件)。
将各物理量参数整理如表1所示。
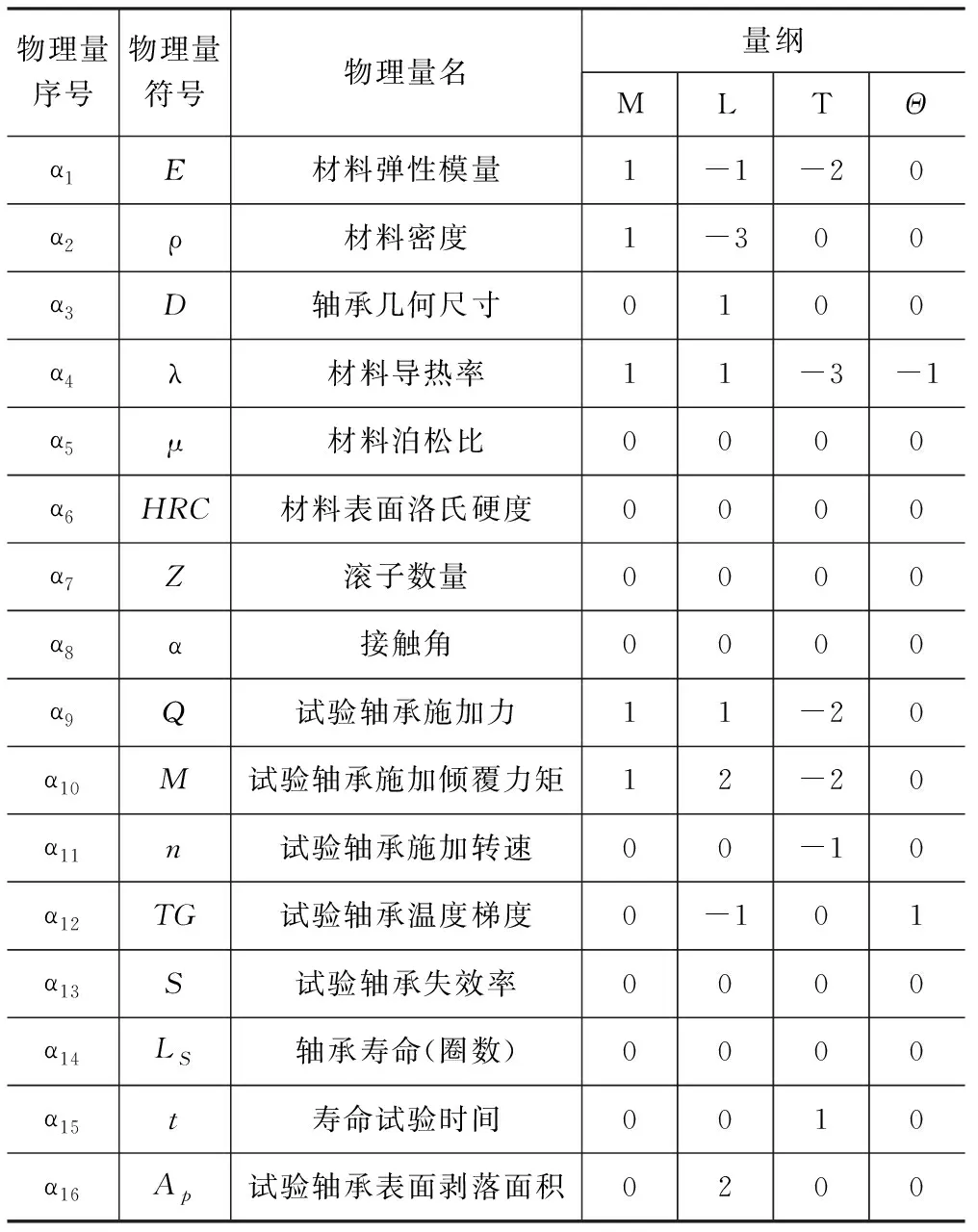
表1 物理量参数表
2.3 量纲分析矩阵计算
依据上文对影响风电主轴轴承物理量的总结,风电主轴轴承的寿命模型的一般函数表达式为:
(4)
写出式(4)的∏项表达式:
(5)
根据∏项表达式及物理量参数表将上述物理量改写为矩阵形式如式(6)所示:

(6)
可以得出r(A)=4,因此应当选择4个量纲互不线性相关且非零核心物理量。为了方便试验加载条件根据模型实验中使用材料的因素以及试验轴承几何尺寸的影响,选择弹性模量E、材料密度ρ、轴承几何尺寸D为核心物理量。令Ax=0,求得解向量的空间基为式(7)所示:
(7)
通过白金汉∏定理,可以求得12个相似准则如式(8)所示:
2.4 准则项结果
根据上文求得的相似准则,风力发电机主轴轴承的模型在满足实现等效寿命分布时应当符合以下基本要求:
(1)根据相似准则Π1、Π2、Π3、Π4、Π9、Π10,模型的无量纲量必须与原型相同。
(2)根据相似准则Π5、Π6、Π7、Π8可以推导出等效寿命模型试验时应当加载的实际工况,满足运动学相似条件和热动力学相似条件。
(3)根据相似准则Π11以推断轴承模型试验总体时间。
(4)根据相似准则Π12可以判断轴承模型的失效条件。
3 模型仿真验证
3.1 模型建立
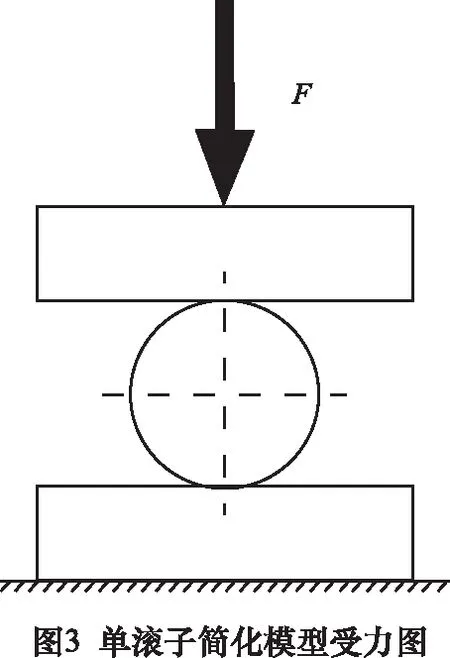
为验证本文风电主轴轴承相似准则的正确性,使用ABAQUS软件和FE-SAFE软件对线接触向心滚子轴承的单个滚子简化模型进行疲劳寿命求解。单滚子简化模型及其受力如图3所示。
3.2 模型参数及时间历程载荷求解
根据标准文件[4]规定,选择轴承套圈及滚动体的材料为G20Cr2Ni4A轴承钢。查阅材料手册[27],各模型与原型各参数如表2所示。根据Π5=E-1D-2Q1,模型施加载荷必满足等式(9):
(9)
根据式9和原型的物理量参数选择施加载荷大小,仿真原型及模型各参数见表2。
7050-T7451铝合金薄壁件铣削仿真建模及试验分析 纪合溪,葛茂杰,于 健,姜 楠,孙卫峰6(15)
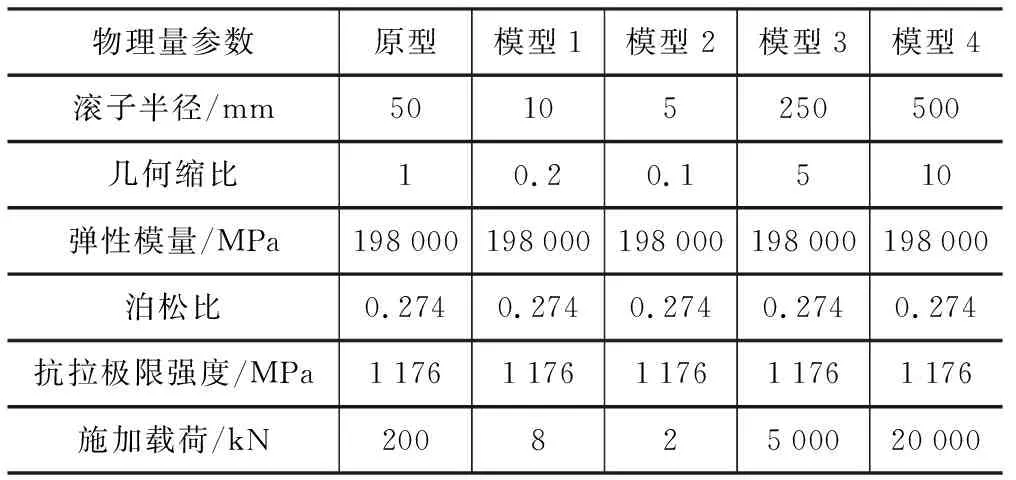
表2 仿真原型及模型参数表
参考Harris等[15]对轴承受径向力下载荷分布的推导,在不考虑径向游隙时,线接触轴承载荷分布符合式(10):
(10)
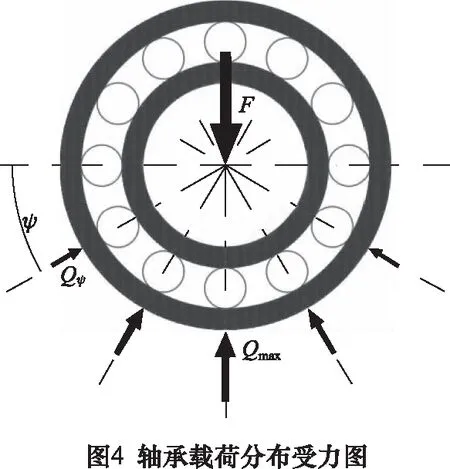
由此可推断出单滚子模型及原型在旋转一圈下的对应法向载荷分布应为图5。图5中x轴表示距离水平线的转角Ψ,y轴表示当前转角下滚子所承受的法向载荷和最大值的比值。由此可以得到单个滚子所受载荷在一个周期下的时间历程。
3.3 模型仿真结果

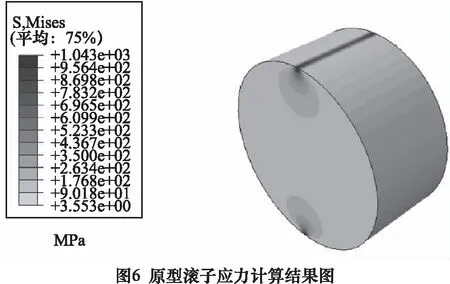
基于上文原型与模型参数以及推得的时间历程载荷进行仿真。首先使用ABAQUS软件建立静力学模型,依据表2中物理量参数算出结果。静力学模型计算结果为图6。通过图6的Mises应力云图可以判断出滚子上下接触点的应力最大,是疲劳计算的危险点。
再使用FE-SAFE软件导入静力学计算结果。接着依据表2的弹性模量和抗拉极限强度使用Seeger算法求出G20Cr2Ni4A轴承钢材料的应变寿命和S-N曲线数据。参考文献[28],由于G20Cr2Ni4A轴承钢材料是韧性材料,因此美国汽车制造商协会推荐采用的首选算法为Brown-Miller算法。同时,由于S-N曲线是在平均应力为零的对称循环应力条件下测得的,所以仿真计算中通过Morrow平均应力修正,减去每个循环周期的平均应力,修正弹性应力大小,使预测的疲劳寿命更接近实际的疲劳寿命。步骤省略,运算结果如图7。
将图7结果整理为表3。忽略有限元的微弱误差,从表3可以看出不论几何缩比如何变化只要符合本文所提出相似准则单滚子模型寿命计算结果几乎相同。

3.4 仿真结果阐释
仿真模型与原型之间实现等效寿命也可以基于疲劳失效理论做出进一步阐释。不论模型几何缩比多少,在符合相似准则Π5=E-1D-2Q1时,模型与原型的静力学计算结果符合应力场相似。其危险点所承受的应力变化历程相同,当使用相同的累计损伤理论做假定时,计算的寿命结果必然也相同。如此,进一步证明了求得相似准则的正确性。
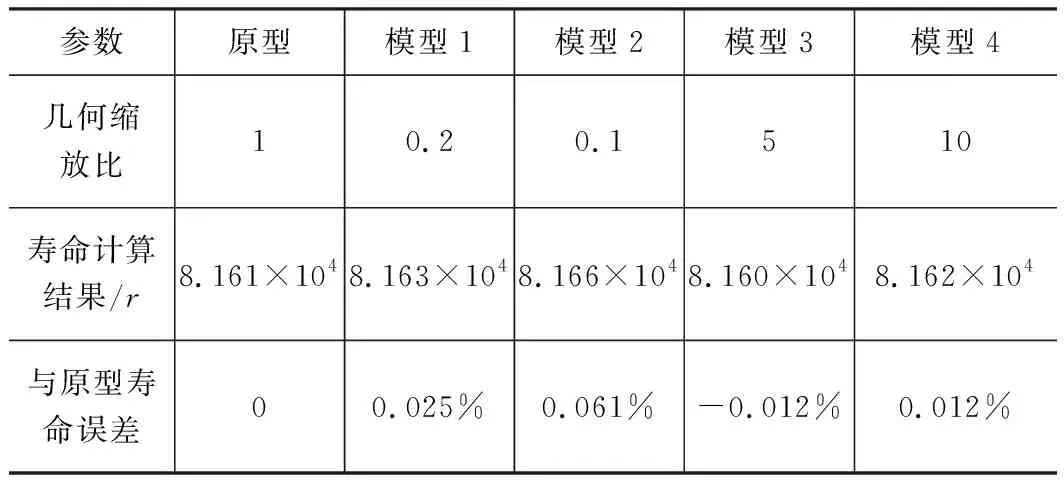
表3 原型及模型寿命仿真结果表
4 结语
本文从相似理论方法入手,基于风力发电机主轴轴承的寿命理论,使用量纲分析法求出等效寿命的相似准则,最后通过单滚子的模型仿真验证了相似准则的准确性。结论如下:
(1)风力发电机主轴轴承的等效寿命模型应当遵循无量纲物理量相等,且符合几何相似。
(2)模型应符合运动学相似,当材料相同时,加载转速由尺寸的缩小而反比例增大。
(3)模型应符合动力学相似;当材料相同时,试验台加载的径向力比值应当为尺寸缩比的平方,试验台加载倾覆力矩比值应当为尺寸缩比的立方。
(4)本文所推导的相似准则为风力发电机主轴轴承模型试验的准确性奠定了理论基础。

