面向云制造的订单资源分配方法
苑明海 张理志 朱雅萍 李亚东
(①河海大学机电工程学院,江苏 常州 213000;②南通河海大学海洋与近海工程研究院,江苏 南通 226300)
当今,个性化产品需求的不断增长,制造企业必须探索改善生产方式,增强企业竞争力的新途径[1]。云制造(CMfg)作为一种新型智能制造模式,它出现使许多位于不同地点、生产能力和规模的企业结成了企业联盟[2]。企业联盟基于CMfg服务平台,建立了用于产品设计,制造和其他生产周期活动的分布式协作制造模式[3]。
在云制造服务平台下,如何快速实现各生产单位间的订单资源有效分配就具有重要的研究价值和意义。一些学者为云调度做出了贡献,李帅等[4]提出了面向突发事件的分布式制造中的资源调配模型,并用粒子群算法进行求解。周龙飞等[5-6]研究了企业车间资源的调度情况,阐述了CMfg调度的原理和复杂性,提出了一种事件触发的动态任务调度方法。邰丽君[7]等构建了资源服务目标调度模型,并针对服务组合时可能出现的突发问题,提出了一种动态调度技术。彭运芳等[8]基于模糊理论提出了一种改进的遗传算法,解决在不确定条件下的车间调度问题。张国辉等[9]分析了车间实际生产中工件移动时间的情况,构建了柔性车间作业调度模型。刘波等[10]针对多任务时组合效果不佳的问题,提出了面向复杂任务请求的服务组合优化框架。在云环境中,王旭亮等[11]使用分支剪切算法来解决跨企业、多约束、多品种和小批量生产和调度问题。一些学者还从服务优化组合,分配模型的建立,任务分解[12-13]中总结了云调度。
上述文献为云调度做出了贡献,但是,云制造中的订单资源分配仍然存在数学模型的完整性、约束条件的设置、解的有效性以及算法的复杂性等问题。因此,本文充分考虑了每个订单的生产约束,构建了完整的订单分配模型,并提出了一种改进的多层编码遗传算法进行求解。在实践中,成本仍然是企业最重要的因素,因此,本文以制造成本、物流成本以及罚款成本为调度目标。最后,通过实例验证了其可行性和有效性。
1 云制造订单资源的调配问题描述
1.1 调配问题数学描述
多任务资源调配问题可描述为:
x=[x1,x2,x3,...,xn]T
Miny=f(x)={f1(x),f2(x),f3(x),...,fm(x)}(1)
y=f(x)={f1(x),f2(x),f3(x),...,fm(x)}
式中:x为任务决策向量,y为目标向量,f(x)为任务决策向量x对应的目标函数,gj(x)为任务x的第j个约束条件,S为其要满足的解域。
1.2 云制造订单资源调配描述
云制造环境下,企业联盟(EU)下属有e个制造企业且分布在不同区域,各制造单位由联盟统一调度部署生产p种产品。假设在给定的计划期T内,EU获得若干产品订单,将订单分配给e个制造企业生产,求调配模型的最优目标值。
在订单调配模型中作如下假设:
(1)各制造企业在接到产品订单前,无在制品、产成品或缺货累积情况。
(2)各制造企业按订单量生产,计划期内一旦开始,过程中不允许中断,直至生产结束。
(3)各制造企业的生产线按计划期最大生产量生产,其最大生产量是综合考虑设备、员工、物料等约束确定的。
(4)生产过程中,不存在次品或伪劣品;每个制造企业在计划期内对同一产品的制造成本都一样。
(5)产品生产制造过程中,各制造单位运输方式固定,且时间成本已知。
为更好地对调配模型进行后续的研究,从而对模型中涉及到的参数进行统一说明,具体如表1所示。

表1 参数定义及说明
表1中,企业编号参数i= 1, 2,…,e。
每个订单对应一种产品类型,如果原始订单包含若干个种类的产品,则对原始订单重新拆分成若干个子订单,订单编号用参数r来表示。例如:产品订单A,包含a和b两种类型,则对应的子订单可编号为1和2。原始订单中若没特别指出,都按照拆分子订单进行编号。假设在计划期[1,T]内,拆分后重新编号的子订单总数为N,r= 1, 2, … ,N。
每个订单都按计划期生产,违反计划期约束的解将给予惩罚,将产生额外的惩罚成本。参数dr是产品订单r的最后交货期限,逾期将交付相应的惩罚成本。
bri为0-1变量,表示企业i生产订单r的能力。其值为1,表示企业i具有生产订单r的能力;bri为0时,表示不具有该能力。
xri(t)为0-1变量,表示企业i按期交货的能力。当xri(t)=0,表示订单r不在该企业i生产,不能按期交付;xri(t)=1,表示产品订单r在企业i生产,并能在t计划期按时交付。
zri为订单r在企业i的开工期,则完工期为zri+Tri。例如:第t时段,开工期即为t时段起点,完工期即为t时段末点,同样交货期dr也为t时段末点。
2 订单资源调配模型的建立
云制造环境下,企业联盟基于各企业的制造能力和订单约束条件,对订单资源进行合理调配,过程中需要充分考虑产品订单的制造成本,运输成本,惩罚成本,使其目标总成本最小。所以本研究主要从产品订单制造成本、运输成本和惩罚成本3个方面建立目标函数。
2.1 目标函数的建立
(1) 制造成本
计划期[1,T]内,产品订单r在企业i生产,单位制造成本为sri,则产品订单总制造成本为:
(2)
(2)运输成本
订单r在企业i生产时,产生的运输成本为cri,由于运输方式固定,所以总运输成本为:
(3)
(3)惩罚成本
在实际生产过程中,企业在订单生产时,可能会出现提前或拖延完成生产任务的情况,与其产品的订单价值vr相关联。设提前/拖期情况的惩罚因子分别为α和β,则订单r的提前/拖期惩罚成本为:
(4)
由于总惩罚成本包含提前和拖期两种情况,则总惩罚成本为:
(5)
综上所述,订单调配模型的目标函数可定义为:
(6)
2.2 约束条件
(1) 订单生产约束
一个订单只能由一个企业生产,故有:
(7)
(8)
bri,xri(t) ∈{0,1}
(9)
式(7)保证每个订单只能由一个企业生产加工;式(8)确保每个产品订单r企业i能够准时交货;式(9)变量xri和bri是0-1变量。
(2)生产能力约束
企业联盟下,各个企业制造能力不同,因此只有具备此种产品的生产能力才能进行生产,否则就不能生产。故有:
(bri-1)·xri(t)≥0
(10)
(3)开工期约束
开工期约束即表示某企业在订单产品生产时,必须保证前一个订单完成后才可以开始新的订单。
为充分考虑各企业产品生产的可能性,本文从产品订单r的最早开工期,最晚开工期,以及计划期约束3个方面进行开工期进行约束。具体如下:
(11)
式(11)表示订单r的最早开工期zri不能早于企业i生产其他订单的最晚完工期的下一个计划期[14]。
(12)

同时,针对订单r、开工期、制造周期和运输时长应满足如下约束:
(zri+Tri+tri-t)·xri(t)=0
(13)
2.3 订单资源调配模型
综合上述分析可得,订单资源调配模型为:
(14)
s.t.
(15)
(16)
bri,xri(t) ∈{0,1}r∈N,i∈e,t∈[1,T]
(17)
(bri-1)·xri(t)≥0r∈N,i∈e,t∈[1,T]
(18)
r∈[1,N],i∈[1,e],t∈[1,T]
(19)
(20)
(zri+Tri+tri-t)·xri(t)=0r∈[1,N],i∈[1,e],t∈[1,T]
(21)
3 改进多层编码遗传算法的设计与实现
上述的模型函数,是一类典型的非线性多约束优化的复杂问题,涉及到的参数多,对应的数据量也庞大,针对这类问题一般采用智能算法来求解。为清楚的表达各订单对应生产企业的有效配置,本研究采用改进的多层编码遗传算法来求解。首先,通过采用整数编码的方式将订单个体编码并分为多层,每层编码对应不同含义,一起完整表达问题的解,实现了一条染色体多层编码表示复杂问题的解,同时引进个体浓度的概念,使其具有更强的适应性。
为更好地阐述改进多层编码遗传算法的求解过程,以5实例验证部分,表3~6数据资料中计划期在[1,10]内的1-8个子订单为例进行详细的说明。
3.1 整体模型
本文采用整数编码的方式来进行编码,每个染色体表示产品订单的调配生产顺序。基于产品订单资源调配生产的特点,提出基于订单编号和加工企业的两段式非负整数编码方法。如图1所示。

图1对应的个体为:
[4736125831324214]
该个体表达了8个订单在4个加工企业的生产顺序。其中前8位表示订单的编号,后8为表示4个加工企业的调配生产顺序。
第一部分基因依据订单的编号进行编码。其中基因长度对应订单的个数,编码的先后顺序表示订单的先后加工顺序。
第二部分基因依据企业编号进行编码,且编号与第一部分中订单的生产企业对应。
3.2 初始种群的生成
随机生成初始种群M,定义为M={u1,u2,···,um},其中um表示群体M中的个体,构成问题的初始解。
3.3 适应度函数的计算
适应度函数反应每条染色体的优劣程度。本文的研究目标是求订单生产总成本的最优值,因此采用订单模型函数为适应度函数。
(22)
以图1中个体为例,根据解码过程,计算适应度函数值。
(1)构建订单生产顺序矩阵A
将上述染色体解码,得到生产顺序矩阵A。矩阵A中第一列代表生产企业编号,每一行从第二位起表示在该企业生产的订单编号。

(2)构建制造成本矩阵AM
根据矩阵A,表3和表4的数据资料,由制造成本函数(2)可得:
根据矩阵AM,可求得总制造成本为MC=520.9.
(3)构建运输成本矩阵AT
根据矩阵A,表3和表5的数据资料,由运输成本函数(3)可得:
根据矩阵AT,同理可求得总运输成本TC=47。
(4)计算提前/拖期惩罚成本
根据矩阵A和表4的数据资料,构建订单生产计划期约束矩阵AR和订单产品数量约束矩阵AA,得:
根据开工期约束,式(19)~(21),表3~6的数据资料,计算可得订单的生产调度矩阵为AS.
由矩阵A和矩阵AS可知在计划期内1-8子订单的生产调度方案。如表2所示:
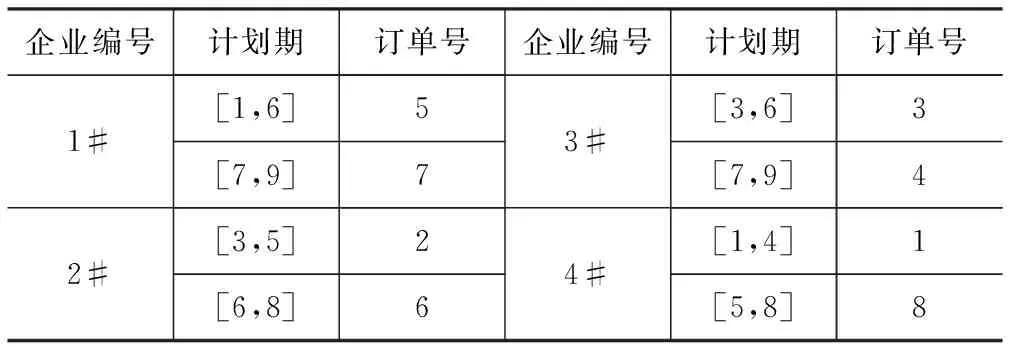
表2 1-8子订单生产调度方案
根据矩阵AS和表4的数据资料计算提前/拖期的惩罚成本,可得:5#订单拖期3天,惩罚成本为60;7#订单拖期3天,惩罚成本为69.6;6#订单拖期1天,惩罚成本为12;8#订单提前1天,惩罚成本为9。其他订单准时交付。
所以,总惩罚成本为PC=150.6。
(5)计算总成本
根据目标模型函数,可得fTotal=Mc+Tc+Pc=718.5。
3.4 遗传操作
(1) 亲本选择
为保证适应度好的染色体能够被选择,本文采用轮盘赌法对个体进行选择操作。种群的规模大小为M,个体Chromi的适应度值为fitness(Chromi),则其被选择的概率为:
(23)
由于轮盘赌法常会出现适应度值优的个体未被选入到下一更新群体的情况,同时会出现局部收敛的现象。为此,引入个体浓度对选择算子进行了改进操作。
首先,从种群M中,找出个体属性相同的个体,并将其归为j类(j=1,2,…,n)。那么个体浓度为:
(24)
式中:rj表示第j类的数目。

(25)
则个体的选择概率为:
(26)
式中:ζ∈(0,1)为选择权重系数。
因此,目标值越小代表该染色体越出色,适应性越高,选择概率就越大,算法的收敛速度也越快;同时,个体的浓度越大,相应的选择概率就越小,从而避免了“早熟”的现象。
(2) 交叉操作
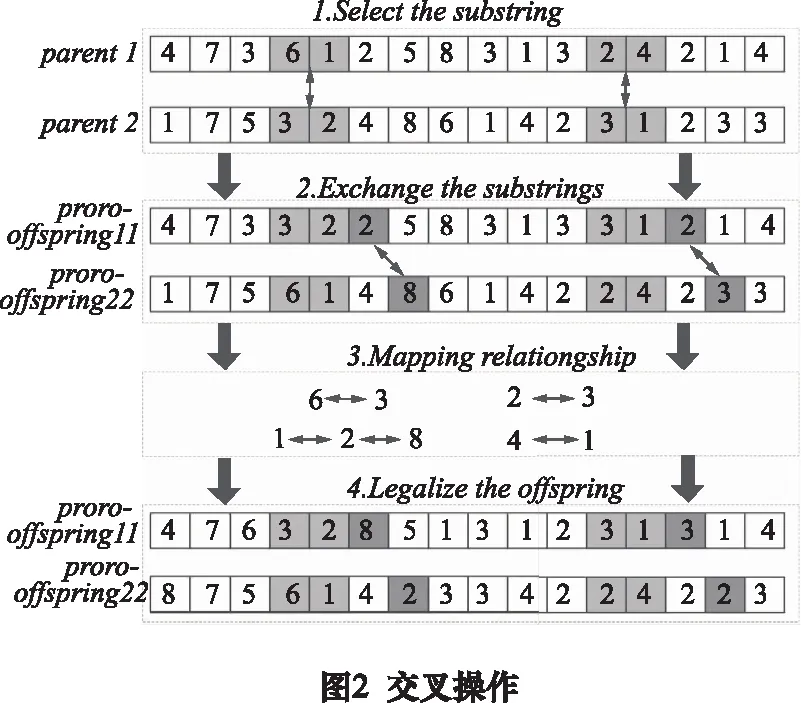
交叉算子是算法搜索求解的主要算子,交叉率的选值范围一般为pc∈[0.2,0.9]。基于上文的编码方式,选用整数PMX(partial-mapped crossover)交叉方式进行交叉操作,避免交叉过程中产生的非法染色体。具体操作如图2所示。
(3) 变异操作
变异操作能够保证了均衡的全局和局部搜索能力。种群规模大小,编码方式和长度等因素都会对变异率的选取产生一定的影响,一般取值比较小,范围为pv∈[0.001,0.1]。
根据个体编码特点,变异操作即从染色体第一部分随机选择两个变异个体,对应位置position1和position2,交换两位置改变其调配的先后顺序,第二部分则按照position1和position2对应的position3和position4上的生产企业编码做同样的调换操作。具体如图3所示。

(4) 精英保留策略
在交叉变异后,为了让适应度较好的父代染色体能够保留下来,将其与子代进行适应度值的比较,保留适应度较好的染色体。
4 实例验证
为了检验所设计的改进多层编码遗传算法求解订单调配问题的有效性和可行性,以某企业联盟的生产订单数据资料进行数值仿真分析与验证。
EU下属有某4家企业共可生产a、b、c和d这4大类型产品。假设在计划期[1,20]内,EU接收到客户的8大产品订单生产需求,根据订单的产品类型和各企业的制造能力对8大产品订单进行重新拆分和编号,将其分成若干子订单,并将这些子订单分别定义为1, 2, 3, … , 16。在进行订单生产时,企业生产能力如表3所示,对应的订单信息如表4所示,企业计划期内的最大生产量如表5所示,生产过程中产生的运输时间和成本如表6所示。为保证各成本处于可接受的水平,设定提前,拖期交货的惩罚因子为α=0.1,β=0.2。
算法仿真的参数设定:种群规模为50,交叉概率为0.8,变异概率为0.1,代沟为0.9,最大遗传代数为50,算法终止。根据订单的实际需求或专家评定,惩罚函数的权重系数为α=0.1,β=0.2。在编码计算过程中,对应产品编号如表7所示。
通过仿真运算,得到改进多层编码遗传算法搜索过程如图4所示。同时,最优个体对应的产品订单在1#企业-4#企业的调配方案如表8所示。产品订单分配加工甘特图如图5所示,其中101表示1#企业生产1#订单产品a类型,其他的依次类推。为直观的表达本文设计算法的有效性,在参数设置相等的情况下,采用一般的遗传算法(genetic algorithm, GA)与本文的改进的多层编码算法(improved multi-level coding GA, I-MCGA)进行仿真试验对比,得到的一般算法搜索过程如图6所示,各目标结果值对比情况如表9所示。

表3 企业联盟(EU)的bri和sri值


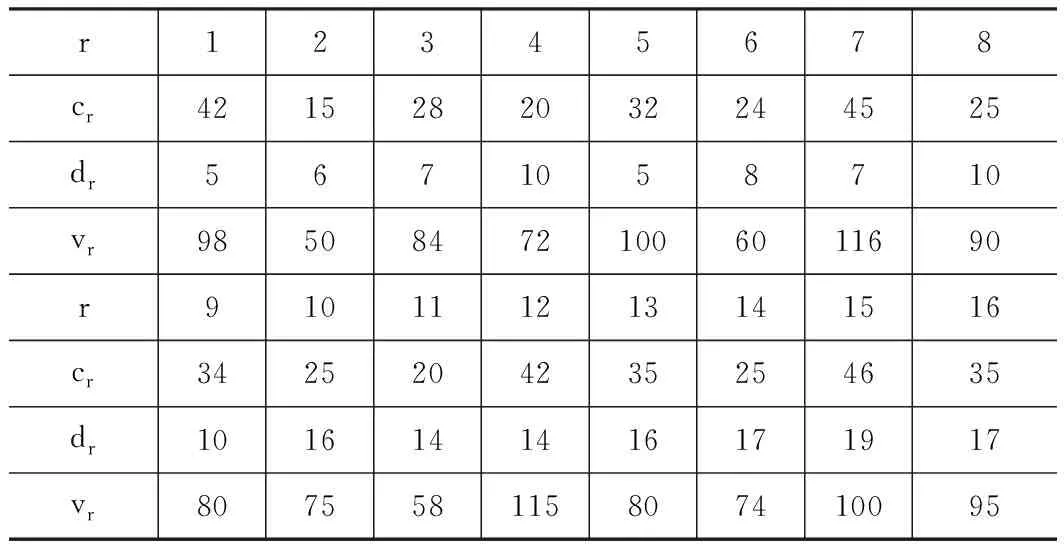
表4 订单信息
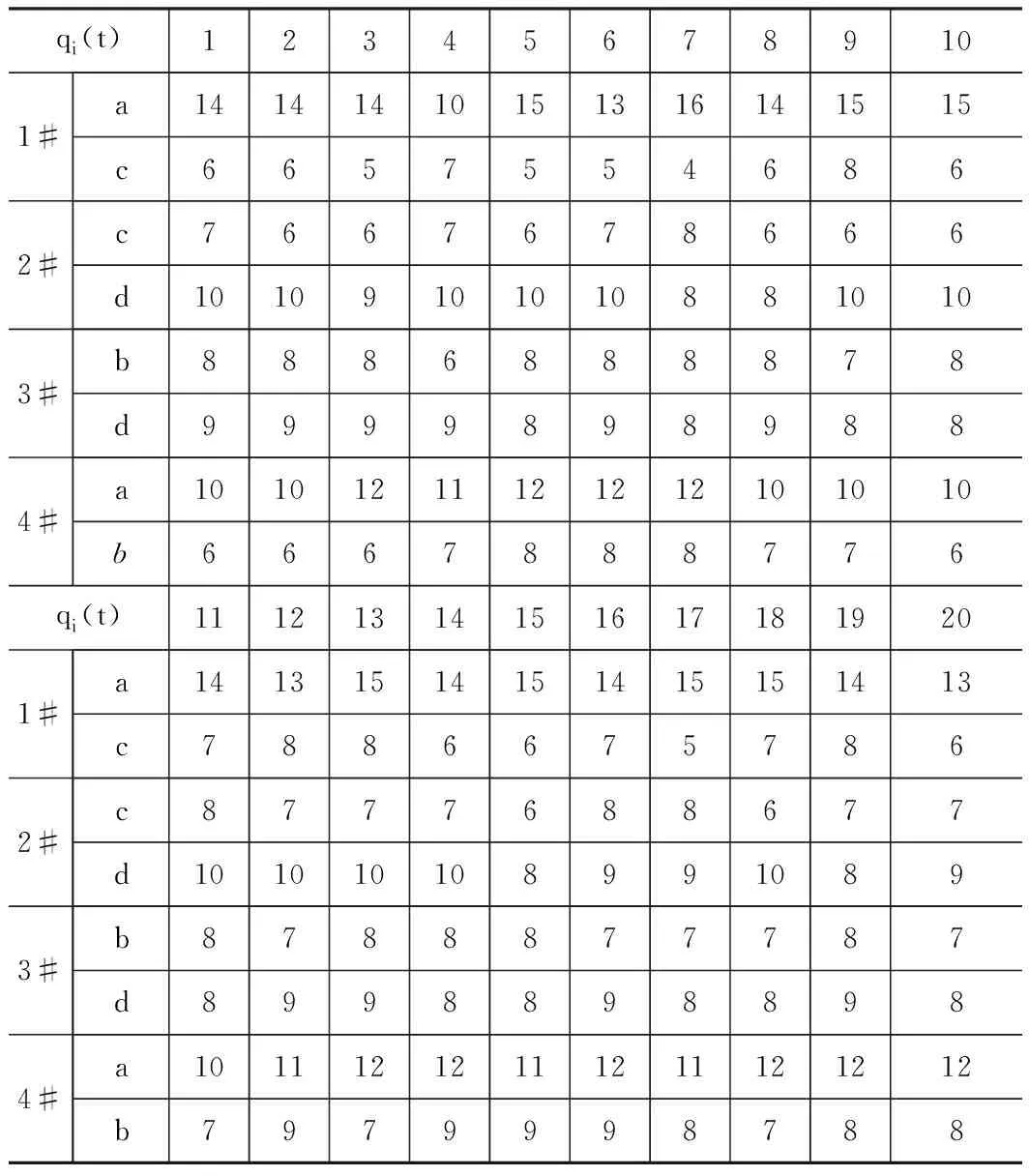
表5 企业联盟(EU)在[1,20]计划期内的最大生产量qi(t)

表6 订单在企业联盟(EU)的运输时间tri和运输成本cri


表7 产品类型对应编码

表8 产品订单调最优解

表9 不同算法的对比结果
表8列出了最优个体中各订单中各产品类型在各企业生产分配之间的关系,对应的加工甘特图如图5所示,此时最小目标值为1 285.1,其中制造成本为1 055.4,运输成本为91,惩罚成本为138.7,末计划期为18,满足产品生产的最晚计划期要求。从图4和图6对比可知,本文设计的I-MCGA比一般GA更早趋于收敛,寻优能力有了较大提高。从表9不同算法对比的结果来看,本文的I-MCGA具有较高的搜寻最优解性能,得到的各目标成本优化结果都有较大提升。从而证明本文设计的算法具有更强的寻优求解能力,同时也说明本文设计的产品订单调配模型也是合理有效的。云制造企业联盟可以将求解的最优解应用到实际的生产分配中去,不仅可以提高产品的生产效率,也可以增加企业的经济效益。
5 结语
本文研究了CMfg环境下的订单分配问题,根据制造特点和生产需求的多样性建立了订单分配模型。将包括制造成本,运输成本和罚款成本在内的总成本用作计划目标。考虑订单生产能力,从3个方面对模型进行了进一步测度:最早的开放时间,最近的开放时间和等式约束。然后,设计了一个I-GAMc来求解该模型,在该模型中建立约束矩阵,改进选择算子,并将整数PMX用于交叉运算。最后,通过实例验证了该模型和算法的可行性和有效性。但是,本文仅从企业层面研究订单分配。实际上,还需要考虑其他级别。将来,需要研究更高效,更稳定的调度算法。基于大数据,数据挖掘和机器学习的云制造调度也将是未来的重点。

