基于二阶矩信息的五轴数控机床几何误差建模

信世豪 张立强 李宇昊

(①上海工程技术大学机械与汽车工程学院，上海 201620;②上海拓璞数控科技股份有限公司，上海 201100)

科学技术的高速发展带动了制造业的发展，数控机床日渐成为需要高性能机床的现代化制造产业中不可或缺的重要组成部分。在数控机床加工过程中，几何误差、装配误差、刀具磨损、加工热及外部环境等都会造成加工误差[1]。其中几何误差是指由于机床各个部件实际几何参数偏离理想情况导致的误差，是机床的固有误差，是机床误差源中重要的组成部分之一[2]。近年来，许多文献围绕误差建模技术进行了研究，误差建模技术可以为建立误差模型提供理论基础，通过误差模型建立零件制造装配过程中的几何误差与最终机床空间定位误差之间的关系[3]。

文献表明，目前数控机床几何误差建模时通常都假定几何误差为常量[4]，但是五轴数控机床是由多个平动轴和转动轴串联组成的，各运动轴在加工过程共同作用产生误差[5]，因此在同一位置多次测量时，测得误差随机性较强。传统模型没有考虑误差随机分布情况对定位误差的贡献[6-7]。针对这一问题，本文根据C100P五轴数控机床的结构特点，通过测量统计确定各项几何误差分布，基于误差的均值与方差进行误差建模。由于一般情况下几何误差十分接近正态分布，因此本文假设几何误差服从正态分布，以矩阵形式表示机床几何误差，从而将几何误差概率分布情况纳入误差模型。该研究方法也可为其他各类机床建模问题提供参考。

1 基本方法

1.1 误差分析

数控机床是由多个活动构件联动运动的复杂机械系统，由于间隙、形变和切削力等原因不可避免存在误差[8]。传统方法测量误差时，通常将误差视为定值，忽略了其分布情况，实际上，在误差经过传递之后，由于误差随机分布导致的误差将被放大。

假设有两个串联且沿X轴移动的移动副，不考虑其分布情况时，极限误差为μ1、μ2。

以表1中列举的两组误差数值为例，传统方法计算这两个移动副的合成极限误差为μt=μ1+μ2，结果记录于表1第三行；如果考虑误差分布情况，在Matlab中设定误差的均值与标准差，模拟实际运行过程中由于多种原因导致的误差随机分布，再对两个误差进行合成，将结果记录于表1第四行。

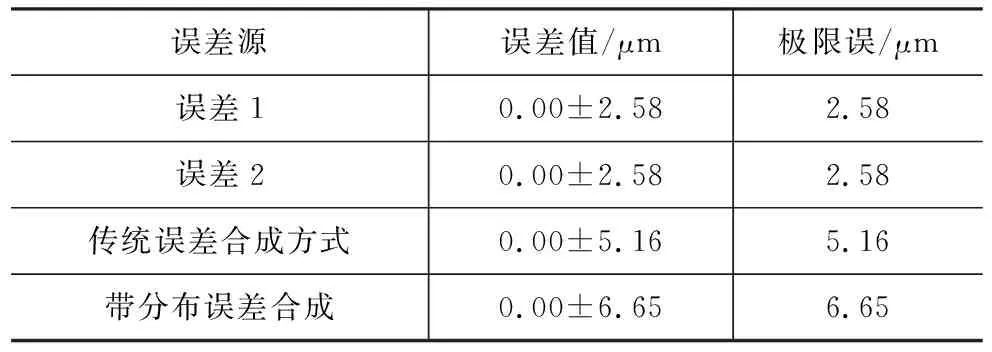
表1 传统误差合成与考虑分布的误差合成

观察表1中两种方法的极限误差可知，考虑误差随机分布情况时，合成误差的极限误差大于传统计算方法算出的误差，这是由于传统误差合成忽略了误差在空间内的随机分布情况而产生的。针对因此产生的误差，本文将考虑误差分布情况，对数控机床进行误差建模，从而提高误差模型的准确度。

1.2 正态随机变量矩阵运算规则

1.2.1 基于二阶矩信息建立误差传递矩阵

多轴数控机床运动副间位姿传递关系可用3项角度误差与3项平动误差组成的传递矩阵表示，如图1所示。

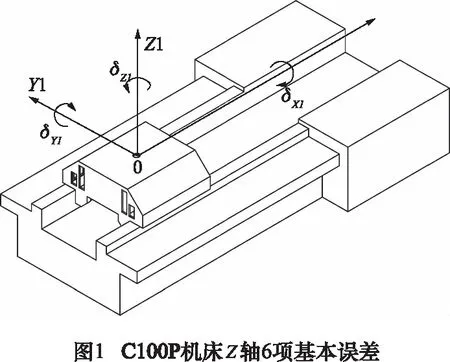
以C100P五轴数控机床Z轴为例，根据齐次坐标变换原理，Z轴相对于床身的误差传递矩阵可表示为：

(1)

为了考虑误差分布情况，引入误差的二阶矩信息来描述各项误差，二阶矩信息即误差的均值与方差，能够准确描述误差在空间中的分布情况，每一项误差都描述为由均值与方差表示的矩阵形式。相比传统齐次坐标变换法建立的传递矩阵，引入二阶矩信息的误差传递矩阵包含了误差的分布情况，能够计算在误差传递后误差分布相互耦合产生的影响。考虑正态化的误差特征矩阵中，为方便表示，将误差项Δx1记作一行二列数组(a，b2)，其中a表示Δx1均值，b表示Δx1标准差。Z轴相对于床身的带分布误差传递矩阵可表示为：

(2)

式中：μ表示误差的均值，o表示误差的方差。同理B轴相对Z轴的误差传递矩阵也可表达为同一形式。则B轴相对于床身的误差传递矩阵可表示为：

MOB=MOZ·MZB

(3)

分析式(3)可以发现，在多体系统运动学中，二阶矩形式的误差特征矩阵包含4种运算：常数与误差项相加，常数与误差项相乘，误差项与误差项相加，误差项与误差项相乘，因此必须确定上述4种运算如何进行，才能使用多体系统运动学方法对误差进行建模。为将带分布的运算符号与数值运算符号区分开来，本文定义符号#+和#*分别为带分布加法和带分布乘法运算符，之后将以#+表示带分布的加法运算，以#*表示带分布的乘法运算。

1.2.2 常数与误差项相加

因为常数c可以看作均值为c，方差为0的误差项，因此可以将常数c表示为(c，0)，根据正态分布函数性质，常数项c与正态分布Δx1相加，均值相加，标准差不变，可表示为：

c+Δx1=(a,b2)#+(c,0)=(a+c,b2)

(4)

1.2.3 常数与误差项相乘

根据正态分布函数性质，常数项c与正态分布Δx1相乘，均值为两者均值的乘积，标准差为两者标准差的乘积，可表示为：

c·Δx1=(a,b2)#*(c,0)=(a·c,(c·b)2)

(5)

1.2.4 误差项与误差项相加

因为Δx1、Δx2为独立正态分布，根据正态分布性质，两个独立正态分布相加，得到的分布为正态分布，均值为两者均值之和，方差为两者方差之和，可表示为：

Δx1+Δx2=(a1,b12)#+(a2,b22)=

(a1+a2,b12+b22)

(6)

1.2.5 误差项与误差项相乘

两个误差项为独立正态分布，即满足

(7)

(8)

在Matlab中创建两个大小相同的符合N(0,1)分布的标准正态分布数列a与b，分析N(0，1)·N(0，1)的性质。创建c=a·b，即满足c=N(0，1)·N(0，1)，使用normfit函数求得c的均值与方差，可得到c的均值为0，方差为1，表达式可表示为：

(9)

分析式(9)可以发现，公式左侧为二次多项式形式，最高次项为Δx1*Δx2且仅有一项，因此可以根据式(3)～(9)经运算得到Δx1*Δx2的分布情况

Δx1Δx2-a1x2-a2x1+a1a2～(0,(b1b2)2)

(10)

进一步推导可得

(11)

Δx1*Δx2的标准差可表示为：

(12)

1.2.6 验证公式正确性

由于均值的四则运算和传统运算相同，因此仅验算标准差的计算公式。

由于Δx1·Δx2运算具有对称性，Δx1·Δx2=Δx2·Δx1显然成立。任取一组不同的均值与方差，另一组保持不变，通过式(12)计算理论标准差。表2记录了实验选取的不同均值与标准差以及经过式(12)计算得到的理论标准差。

表2 选取不同均值与方差检验公式正确性

创建两个服从正态分布的随机变量数组a和b，定义c为这两个正态分布的乘积。从数组a和b中选取随机变量进行数值模拟，求得c的实际标准差并将结果记录在表3中。将表2和表3中的标准差数据绘制在图2同一坐标轴上，比较数值模拟和公式计算得到的标准差。观察图2可以发现通过式(12)计算得到的标准差和通过数值模拟得到的标准差实际值基本吻合，证明了公式的正确性。

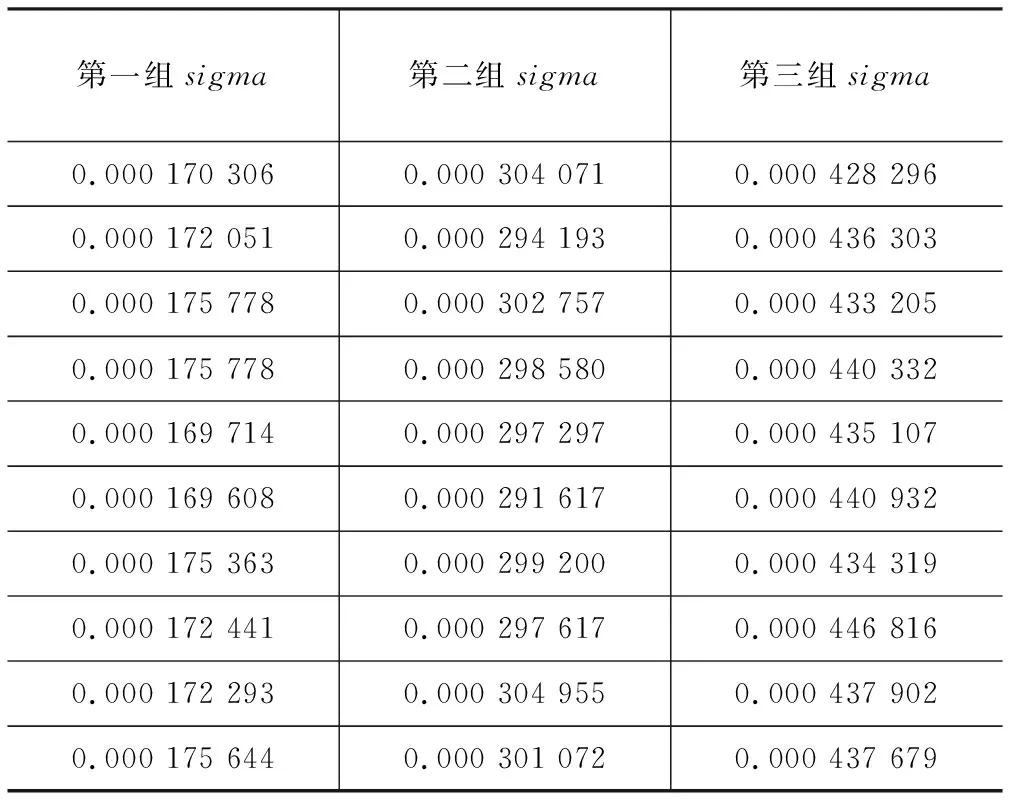
表3 部分标准差数值模拟结果

2 C100P五轴数控机床误差建模

2.1 结构分析

以图3所示C100P转台摆头式五轴数控机床为例，它由床身、摆头(A轴)、转台(B轴)、横向滑台(X轴)、升降台(Y轴)、纵向滑台(Z轴)和主轴组成。

基于多体运动学理论简化机床，由于各部分之间为串联结构，所以可将机床抽象为具有两条分支的树系统拓扑构型。第一分支由床身、纵向滑台和转台构成，第二分支由床身、横向滑台、升降台和摆头构成[9]。

2.2 机床运动矩阵和误差传递矩阵的建立

假设研究对象为C100P转台摆头型五轴数控机床，根据式(3)推导出各运动轴实际运动矩阵并记录于表4。

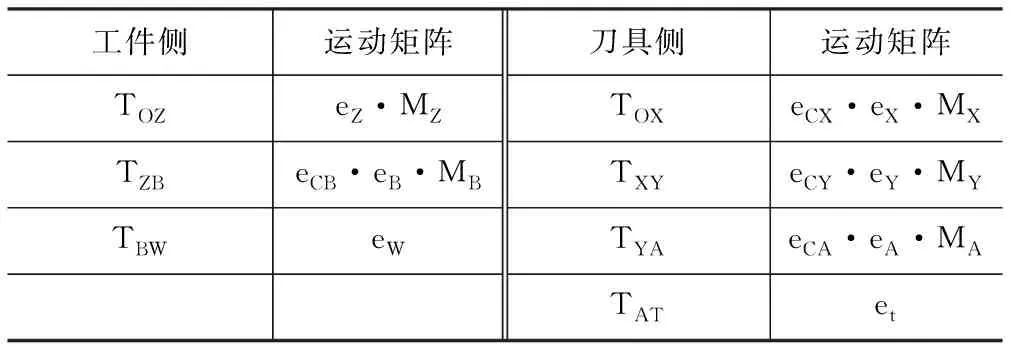
表4 各运动轴实际运动矩阵

表中：MX、MY、MZ、MA和MB分别为X、Y、Z、A和B轴的理想运动矩阵，eX、eY、eZ、eA和eB分别为X、Y、Z、A和B轴平动误差，eCX、eCY、eCA和eCB分别为X、Y、A和B轴转动误差，eW为工件对刀点相对于B轴旋转中心的相对坐标，et为刀尖点相对于A轴旋转中心的相对坐标。

根据各运动轴实际运动矩阵可得到工件和刀具实际位姿矩阵公式的具体形式分别为：

pw=TOZ·TZB·TBW

(13)

pt=TOX·TXY·TYA·TAT

(14)

式中：pw为工件实际位姿矩阵，pt为刀具实际位姿矩阵。同理可以得到工件和刀具理想位姿矩阵公式分别为：

(15)

(16)

pwt=Et-Ew

(17)

pwt′=Et′-Ew′

(18)

机床空间定位误差e即刀尖相对于工件对刀点的理想位置矢量与实际位置矢量之差，可表示为：

e=pwt-pwt′

(19)

3 误差模型实验验证

为了验证误差模型，本文采用对照组的实验方法，测量数控机床几何误差参数[10-11]测量结果记录于表5。针对表5中给出的C100P转台摆头型五轴数控机床误差数据，通过误差模型预测刀具定位误差，绘制图像。

表5 C100P五轴数控机床误差参数

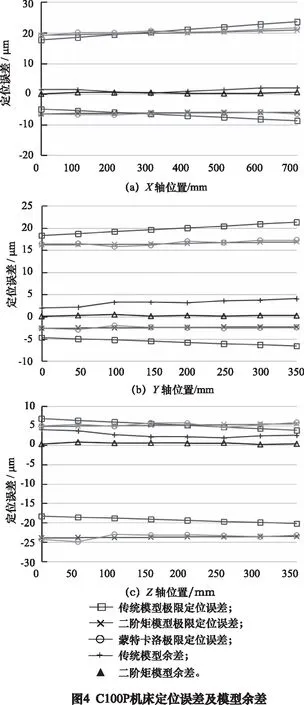
在X、Y和Z三根直线轴上均匀选取8组采样点，将表5中的误差数据代入式(13)～(19)，得到机床理论极限定位误差；计算各项误差的极限误差代入传统齐次坐标变换法计算得到理论极限定位误差；对于实际定位误差采用蒙特卡洛法进行模拟。蒙特卡洛法是一种通过抽样随机原始误差，模拟位姿误差数学模型在计算机上产生与实际加工具有相同统计特征的定位误差数据的数值近似方法。根据表5中的均值与方差分别创建各误差项的随机数组，从随机数组中选取元素计算定位误差，通过多次选取随机数模拟实际加工过程中误差项分布情况，用蒙特卡洛模拟法模拟8次机床实际定位极限误差，并对X轴极限定位误差计算余差，结果输出在图4。

分析图4可知，传统误差模型理论随X轴位置变化预测结果余差均值为1.29 μm，基于误差二阶矩信息的误差模型预测结果余差均值为0.36 μm；传统误差模型理论随Y轴位置变化预测结果余差均值为3.16 μm，基于误差二阶矩信息的误差模型预测结果余差均值为0.25 μm；传统误差模型理论随Z轴位置变化预测结果余差均值为2.65 μm，基于误差二阶矩信息的误差模型预测结果余差均值为0.43 μm。基于误差二阶矩信息建模计算得到的C100P五轴数控机床极限定位误差相比传统齐次坐标变换法具有较理想的预测性能。

4 结语

本文以五轴数控机床为研究对象，通过引入误差二阶矩信息，将误差分布情况纳入误差模型。详细讨论了正态分布随机变量间的运算规则，讨论了带分布误差传递矩阵的建立方法，空间定位误差的计算原理及方法。为了验证该模型的准确性，以C100P转台摆头型五轴数控机床为例，通过测量采集误差数据计算出理论定位误差，与蒙特卡洛模拟法计算出的定位误差进行比较。结果表明，基于二阶矩信息的误差模型能够正确预测数控机床空间定位误差分布情况，具有较好的预测精度。通过与传统误差模型计算结果进行对比，证明了该模型相比传统误差模型能够更加准确地预测机床空间定位误差。为机床空间定位误差的改善提供了参考。