数学概念获得阶段概念教学策略思考
周云

【摘要】在小学阶段,小学生概念学习需要经历概念的感知、理解、巩固、系统化等过程,这一过程也是教师帮助学生建立理解概念、获得概念和巩固概念的过程.一般地,小学数学概念教学通常分为三个阶段:概念感知、概念获得和概念巩固.本文通过分析研究者的课堂教学实践,结合理论基础,提出了在概念获得阶段所采取的一般教学策略.
【关键词】小学数学;概念;教學策略
建构主义认为,知识不是通过教师传授得到的,而是学习者在社会文化背景下,借助其他人(包括教师和学习伙伴)的帮助,利用必要的学习资料,通过意义建构的方式获得的.概念代表事物的基本属性和本质特征,是抽象的.研究者从心理学、教育学等多角度对数学概念教学进行研究后,普遍认为数学概念学习必须建立概念之间的联系,建立概念网络.因此,对小学数学概念教学的实践研究,可在一定程度上丰富概念教学理论;对概念教学现状的分析及策略的探索,有助于为今后探讨概念教学理论提供支持.
学生在初步感悟数学概念之后,会在脑海中形成第一次对概念的自我理解,可能是正确的,也可能存在一些有疑惑的地方,因为此时学生获得的仅是初步的感悟,并没有获得概念,故在感悟概念之后,还要通过有效的概念教学策略进一步获得和建构概念.
一、强化正例,辨析错例
概念的表现方式有许多,但是正例是正确与生动的方式,能够帮助学生理解与强化概念的本质.但仅呈现正例不足以暴露学生最真实的想法,因此在教学中必须要突出错例的作用.在课堂教学推进过程中,会生成大量丰富的学生资源,其中难免会有错例生成,而这些错例的生成恰恰是学生在学习新问题中的“生长元”,教师只有有效地利用这些错例,才能帮助学生扫除学习过程中的困难与障碍,形成对知识内涵的本质理解与体验,从而发展与提升学生的思维水平.
案例实践片段:多连块
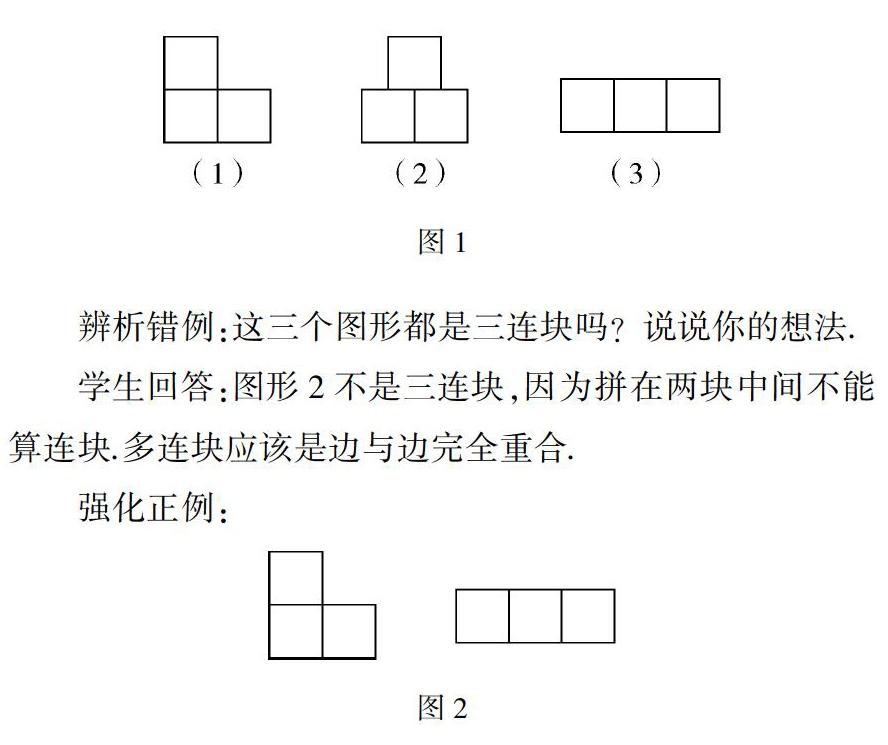
教师提问:请你在两连块的基础上添上一个正方形,使它成为一个三连块,想一想你有几种不同的添法.学生资源:
辨析错例:这三个图形都是三连块吗?说说你的想法.
学生回答:图形2不是三连块,因为拼在两块中间不能算连块.多连块应该是边与边完全重合.
强化正例:
结合两个三连块再一次说一说怎样的图形是多连块.
案例分析:学生在第一环节中通过观看教师的演示,以及多连块的定义,从而形成初步的感知,但这样的感知还没有到达理解程度.
因此第二环节中,教师让学生自主尝试画出三连块,此时要充分暴露学生的想法,将正解与错解一同呈现,让学生谈一谈想法.从生生的互动中再一次辨析得到正确的多连块概念.其实,无论是直接感知的概念还是采用上述其他策略感知的概念,仅仅是第一感觉,往往学生对概念的本质理解还不深刻,因此教师要好好把握学生的“最近发展区”,有效引导,纠正错误,强化概念.
二、多元表征,丰富概念
学生的抽象概括能力会影响数学概念的学习.教师对学生概念的掌握情况主要是通过文字概括来检测.但仅从文字表达来理解数学概念又过于单一和抽象.低年级的学生更需要的是直观经验,因此借助文字、算式、图示等多种表征形式可以丰富学生对概念本质的理解,更能促进其掌握正确的概念,获得良好的概念学习成就.
三、运用变式,理解概念
“变式”是指保持事物内在属性不变,通过非本质属性改变事物的外在形式.顾泠沅教授对变式教学有着深入研究与理论分析,并且将变式教学分为概念性变式与非概念性变式.数学教学中运用概念性变式可以让学生多角度、进一步获得对概念的理解.此外,他还提出“过程性变式”用于概念的形成,目的是为概念建构提供有层次的推进过程.因此,在学生初步感悟概念之后,教师要学会设计变式,在不断变化的过程中让学生建构正确的概念.
案例实践片段:问题解决——比较
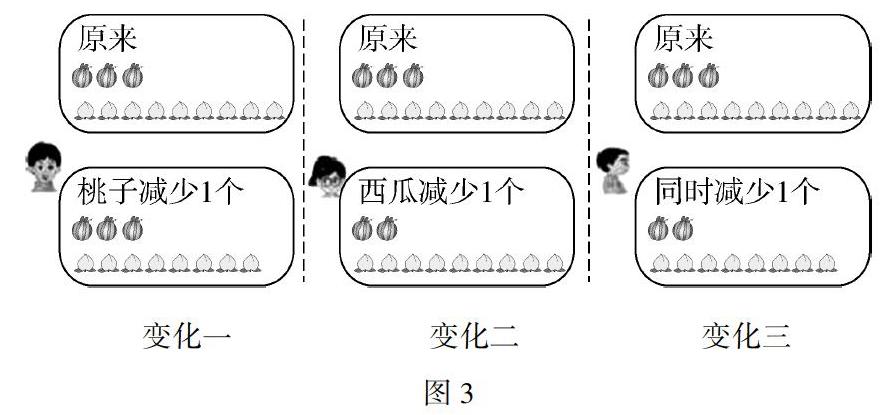
变化一:如果西瓜的个数不变,桃子减少1个,想一想,现在桃子的个数还比西瓜多6个吗?桃子的个数还是西瓜的3倍吗?
变化二:如果桃子的个数不变,西瓜的个数减少1个,那么与原来相比它们之间的相差关系改变了吗?倍数关系呢?
变化三:如果桃子和西瓜的个数同时减少1个,小胖说与原来相比它们的相差关系和倍数关系肯定都变了!你同意吗?说说你的理由.
案例分析:两个量之间可以从相差关系的角度,也可以从倍数关系的角度进行比较.但学生往往会由于各种原因想不到从倍数关系进行比较,或者即便知道从两个角度都可以进行比较,但在遇到不是整倍的情况时会认为不存在倍数关系.在最初教学中,教师从静态的例子引出不是整倍的情况时,发现学生理解起来比较困难.因此,本环节希望能够通过多样的情境,借助动态的变化,降低学习难度,从推理的角度或计算的角度,让学生感受原来两个量之间即便不是整倍也存在倍数关系,也可以用倍数关系进行比较.该过程可将静态的知识呈现在动态变化中,进一步培养学生能力的同时,让学生通过自身的体验,初步建立两个量之间的比较角度,并且在变化的过程中进一步认识几倍多(少)几.
学生在学习概念的过程中会遇到许多变化多样的问题,只要在变化中找到不变,便能真正摸清概念的本质.
四、暴露问题,完善知识
建构主义主张,知识在建构过程中需要通过假设与原认知结构进行分析与再创造,不断重复从而建立概念.而学生在建构知识的过程中避免不了会遇到问题,有些是可以独立解决的,而有些则会影响其建构概念,这就需要教师给予适当的启发和引导.在学习过程中,学生自主暴露问题很难,因此需要教师设计有效的问题引发学生的认知冲突,从而暴露他们的真问题,借助对真问题的理解与辨析完善知识结构.以“轴对称图形”为例:
教师提问:通过观察图4,你们认为它们是轴对称图形吗?
在判断过程中,学生对左图不存在困难,但是对于右图,学生会有歧义.有的学生认为不是,有的学生认为对折之后旋转一下两边就能完全重合了.对此,教师可引导学生从定义思考,明确轴对称图形是沿着折痕两边完全重合,并没有旋转的过程.那么像这样旋转之后能重合的对称图形叫什么呢?此时,教师可告诉学生这样的图形叫作旋转对称图形,它也是对称图形的一类.尽管教师没有完全呈现旋转对称图形的概念,但学生基于最直观的理解至少能明确像这样需要旋转才能重合的图形不是轴对称图形,也从另一个角度强化了轴对称图形的概念.当教师把这一类对称图形的名称告诉学生后,学生的头脑中就形成对称图形的网络框架,如下:
因此,教学时教师一定要注重挖掘学生的真问题,会巧妙设计问题暴露学生的真问题,从而使学生建构正确的概念.
结 语
本研究对数学概念资料、理论的查阅与梳理,对教学策略的探索与实践,使教师对小学阶段数学概念,尤其是这些概念间的联系有了更深刻的理解.在课堂实践的过程中,无论在课堂师生互动方面,还是在教学设计方面,本研究对教师都有很大的帮助,能够使教师更善于解读教材,更清晰新课标的要求.
【参考文献】
[1]邱伟星.小学数学概念教学策略例谈[J].小学教学参考,2019(29):94-95.
[2]薛福山,李天生.小学数学概念教学的策略研究分析[J].课程教育研究,2019(41):158-159.
[3]韩学仁,孔宪云.浅谈小学数学概念教学[J].课程教育研究,2019(39):153.
[4]巨海平.小学数学概念教学的优化策略[J].科学大众(科学教育),2019(09):63.
[5]王春霞.小学数学教学过程中数学概念的培养策略研究[J].科技风,2019(27):34.
[6]王旭.小学数学几何教学中培养学生空间概念的方式探寻[J].名师在线,2019(26):73-74.
[7]杜晶晶.关于小学数学数的概念教学中有效情境创设的研究[J].课程教育研究,2019(37):115.

