基于比较的新教材解读——“空间中点、直线与平面的向量表示”的教材分析与教学建议

朱成万 (浙江省杭州第十四中学 310006)

用空间向量解决立体几何问题，首先要用空间向量表示立体几何问题涉及的几何元素，即把空间中点、直线与平面用向量表示出来，这是向量法的基石，也是学生学习的难点之一．因此，深入理解这一内容非常有必要．

在人教A版旧教材[1](依据2003年版课程标准编写)中，“空间中点、直线与平面的向量表示”这一内容安排在选修2-1第三章第二节(3.2立体几何中的向量方法)，在新教材[2](依据2017年版课程标准编写)中，该内容安排在选择性必修第一册第一章第四节(1.4空间向量的应用)．新旧教材编写差异很大，本文将对这一内容作出解读，以便深入理解空间向量这一核心内容．

1 新旧教材比较

新旧教材的编写，包括编写理念、内容的安排、编写的顺序、素材的选取、例题习题的安排等，差异都很大．本文不面面俱到地研究这些差异，只从以下三个视角对两者作一个比较，以点带面，旨在帮助读者整体地理解空间向量．

1.1 教材编排：一节VS三节

在旧教材中，“空间中点、直线和平面的向量表示”这一内容编排比较简略．在选修2-1第三章3.2节简要地介绍了点的向量表示和直线的向量表示，并用平面向量基本定理表示平面，还介绍了法向量的概念，但各知识点没有详细展开，也没有配套例题．

在新教材中，这一内容很详细.在选择性必修第一册第一章1.4节编排了两块内容，在1.4.1用了 3节详细介绍用空间向量研究直线、平面的关系：“1.空间中点、直线和平面的向量表示；2.空间中直线、平面的平行；3.空间中直线、平面的垂直”，在1.4.2详细介绍用空间直线研究距离、夹角问题．

下面对“空间中点、直线和平面的向量表示”的新旧教材编写内容作比较，列表如下．

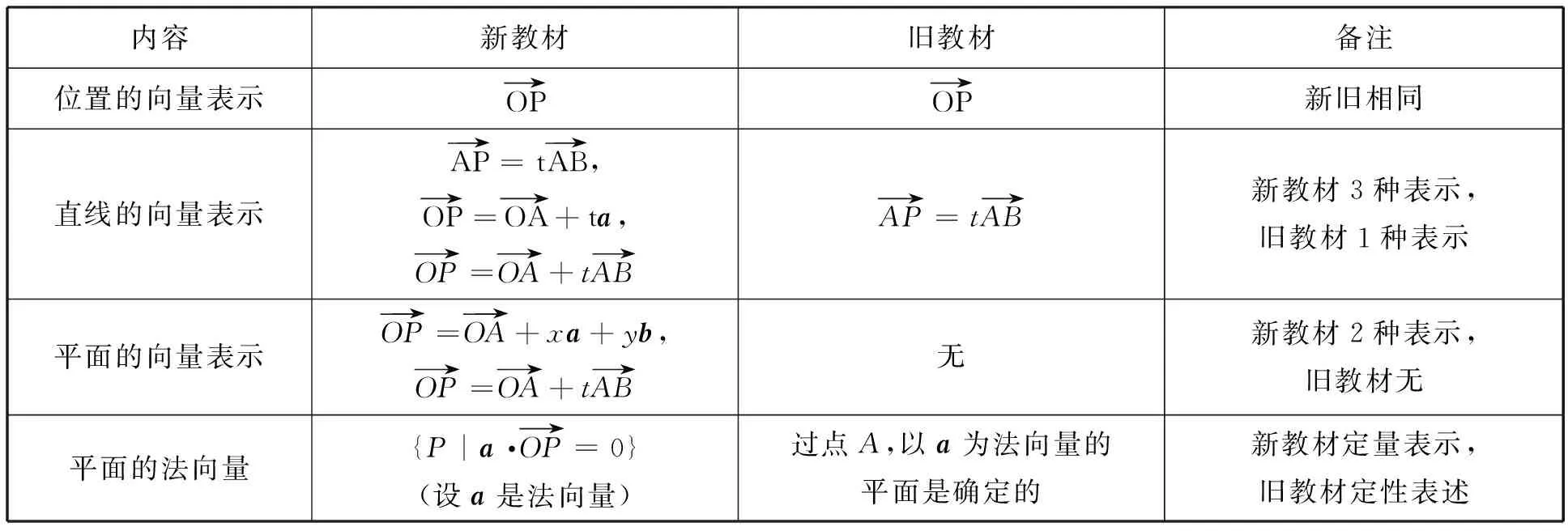
内容新教材旧教材备注位置的向量表示OP→OP→新旧相同直线的向量表示AP→=tAB→,OP→=OA→+ta,OP→=OA→+tAB→AP→=tAB→新教材3种表示,旧教材1种表示平面的向量表示OP→=OA→+xa+yb,OP→=OA→+tAB→无新教材2种表示,旧教材无平面的法向量{P|a·OP→=0}(设a是法向量)过点A,以a为法向量的平面是确定的新教材定量表示,旧教材定性表述

说明：(1)新旧教材内容编排差异很大．总体来说，新教材更详细，内容更多，而旧教材内容相对较少．

(2)新教材将“空间中直线、平面的平行”，“空间中直线、平面的垂直”单独成节，而旧教材只是一带而过．由于该内容不是本文解读对象，所以不列表比较．

1.2 引入思考：一次多问VS多次一问

新旧教材都是以问题引导学习，但是在引入问题的设置上差别很大．表现在旧教材上，设置的几个问题是一次性问完的(图1)．

图1

新教材设置的也是这几个问题(见本文第二部分)，但呈现的方式是问一个问题，解决一个问题．

笔者认为，旧教材一次多问，有问题堆砌的感觉，还有许多问题一次性出来，层次不够分明．新教材问一个，解决一个，这样的编排不仅层次分明，条理清楚，而且学生在学习时目标指向更明确．

另外，具体到每个问题，新旧教材在表述上也有差异．比如新教材的第一个思考问题：“如何用向量表示空间中的一个点？”而旧教材中问题是“如何确定一个点在空间的位置？”笔者认为，新教材的设问直指问题，表述更精确．

1.3 法向量：一带而过VS详细介绍

旧教材介绍了法向量的概念，仅说明可以用法向量解决平行与垂直问题，没有根据点的坐标求法向量的例题，用法向量研究距离、角度问题也很简略．

旧教材对法向量重视不够，这一直是被中学教师诟病的地方，因为在高考中，立体几何大题几乎都是法向量的天下，即教材与高考严重脱节．

新教材弥补了这一缺憾．在编写法向量时，其作了三点改进：(1)不仅介绍法向量的概念，而且给出用法向量表述平面的代数表达式；(2)有配套例题求法向量，包括高考中经常用的根据点的坐标求法向量；(3)加强法向量的应用，在1.4.1节介绍了根据法向量研究平行与垂直的位置关系，在1.4.2节介绍了用法向量研究距离与角度，而且配置了大量的例题．

如此改进，从知识本身看，法向量是重要内容，这样编排主干内容更突出；从实际教学看，做到了学与考的融合，更接地气，更受教师、学生欢迎．

2 新教材逐段解读

下面对新教材进行逐段解读．

2.1 节引言

图2

解读：节引言是先行组织者，具有承上启下的作用．向量从平面推广到空间，既作了数学知识和工具上的准备，也作了学习方法上的准备．

在平面向量中，学生已学习过向量法，即用向量解决平面几何问题的“三部曲”．类似地，用空间向量解决立体几何问题也有“三部曲”：首先要用空间向量表示立体几何问题涉及的几何元素，将几何问题转化为向量问题；然后通过空间向量的运算，研究空间图形之间的平行、垂直等位置关系以及距离、夹角等度量问题；最后将结果翻译成相应的几何结论，得到相应立体几何问题的解决．

这里有个提示作用：下面的学习，自然是从第一步开始，学习如何表示，即如何用向量表示点、直线和平面．

2.2 空间中点、直线和平面的向量表示

图3

解读：开宗明义，明确基本对象是点、直线和平面，研究的任务是对象的表示．这里的逻辑很清楚：用空间向量解决立体几何问题，首先要用空间向量表示立体几何的基本要素，将几何问题转化为向量问题．这是向量法的第一步，也是本节将探讨的重点内容．

图4

解读：“位置是空间的基本概念中最为原始的.在几何学中，通常用点来标记位置，所以点就是位置的抽象化.”[3]要表示位置需要有基点，确定了基点，向量与点就一一对应，如此就可以用向量表示点．用向量表示点，是用向量表示直线和平面的基础，具有奠基作用．

另外，图中的平面用于衬托立体感，这是用图形语言表述数学对象的需要．

图5

图6

解读：因为直线和平面都是点的集合，所以顺着点的向量表示提出直线和平面的向量表示问题是自然的．

实际上，直线由点与方向确定，在平面解析几何中也有体现，比如直线的点斜式方程，其中斜率是倾斜角的正切值，刻画直线的倾斜程度，代表着直线的方向．

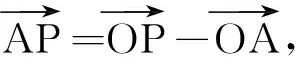
图7

解读：接下来就是探究用向量表示平面，即寻求平面的代数表示，让平面也带上方向，就可以通过向量运算研究平面．

教材给出了平面的两种表示，一种是基于平面向量基本定理，通过向量的线性运算表示平面，另一种是基于平面的法向量，通过向量的数量积运算表示平面．两者表示方式的不同，实际上是基于运算的不同，这体现了向量运算的威力．

图8

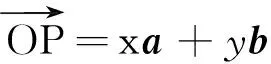
图9

由于这个结论的证明过程显而易见，前面介绍直线的向量表示时也有同样的旁白(图6)．笔者认为这两个旁白只需一个就够了,建议介绍直线的向量表示时给出证明，去掉那个旁白．

图10

解读：前面表示平面时需要用到三要素——一点和两个方向．教材这里用两要素——点和直线，体现了求精求简的思想．

图11

解读：新教材突出了法向量的地位，法向量就是平面垂线所在的方向向量．“直线的方向向量与该直线上的任意向量平行”，“平面的法向量与该平面内的任意向量垂直”，这是方向向量和法向量的本质．

实际上，教材选择“点向式”表示直线和“点法式”表示平面，是内容自身的需要(突出方向向量和法向量的作用)．这里的目标是要将一条确定的直线或一个确定的平面用向量表示出来，而并不是为了将我们曾经学习过的确定直线(或平面)的每一种方式用向量去“翻译”过来．

2.3 例题

图12

解读：例1给出了求平面法向量的具体方法.求平面的法向量是本节的重点，也是难点，两个小题分别代表了两种常见问题类型．旁注中还说明了方向向量和法向量的“不唯一”性．虽然我们并不需要过于强调，但“不唯一”性是客观存在的事实，这一点在解题过程中已经得到体现．同时，本题为后面研究直线、平面间的位置关系，距离和夹角等度量问题作了准备．可以毫不夸张地说，一线教师之所以喜欢这套新教材，很大的原因是教材安排了例1．

3 教学建议

3.1 以问题引导学习

新旧教材都是以问题引导学习，对教学有很大的启示作用，我们在教学时可以采用这一方式．新教材为研究“空间中点、直线和平面的向量表述”提出了三个思考，在教学时，我们可以借助这些思考，但是要根据课堂的实际提出一些追问．

比如，提出思考“一个定点和两个方向能否确定一个平面？如果能确定，如何用向量表示这个平面？”可以进一步设计以下问题，引导学生探究用向量表示平面．

问题1：什么是平面向量基本定理？

设计意图：在最近发展区提问，回顾旧知识，并在此基础上学习新知识．

问题2：如何用平面向量基本定理描述平面内任意一点P的位置？

3.2 加强法向量的教学

法向量为解决立体几何问题提供了一个通法，所以要引起足够的重视．加强法向量的教学，可以从以下几个方面着力．

在法向量概念教学时，需从自然语言、图形语言和符号语言三个角度对法向量进行表示，明确法向量的概念，突出法向量的本质——与平面内任意向量都垂直．

在求法向量时，特别是例1的教学，要归纳出求法向量的一般方法和步骤．

方法1 根据线面垂直的判定定理求法向量；

方法2 根据向量的坐标表示，联立方程组求法向量．

在后续的学习中，用法向量研究空间图形之间的平行、垂直等位置关系以及距离、夹角等度量问题，在空间向量的应用中加深对法向量的理解．