基于“四个理解”的数学抽象素养的培养策略——以函数的导数为例

杨茂涛 李红梅 (西华师范大学数学与信息学院 637002)

随着社会的发展，人的各方面综合素质在不断地提高，社会对人们的要求也在不断地提升．近年来，教育界谈论话题离不开核心素养，其对于学生的发展起着至关重要的作用．有关核心素养从育人的角度上来看，需要培养学生的综合素质，促进德智体美全面发展，使学生具备适应终身发展和社会发展的必备品格和关键能力[1]．将核心素养渗透到数学学科中，其目的就是培养学生的数学核心素养，最终目标是让学生会用数学的眼光观察世界，会用数学的思维思考世界，会用数学的语言表达世界[2]．在数学课堂中要让学生感悟数学的基本思想，体会数学的本质，帮助学生树立正确的价值观，养成优良的品格，促进学生数学核心素养的发展．

1 数学抽象素养

数学抽象素养是学科育人目标中非常重要的内容.在课堂教学中，教师要在理解数学、理解学生、理解教学、理解技术的基础上培养学生的数学抽象素养．章建跃博士[3]提到理解数学，是指理解数学的本质特征，让学生感受数学抽象性的特点；理解学生，是指理解学生的思维规律和认知特点，在了解学生的基础上培养学生的发散思维，进而提高学生的数学抽象素养；理解教学，是指理解教学的基本规律，在教学过程中帮助学生感悟数学思想，掌握基本知识技能，将抽象的数学概念转化为学生易于理解的数学知识；理解技术，是指通过一定的信息技术，将抽象的内容直观地展示给学生，将抽象的过程可视化．

数学抽象素养贯穿于数学教学的全过程，数学抽象素养能力的提升，对于学生全面发展有很大的帮助，教师要给予一定的重视，培养学生数学抽象素养，帮助学生更好地理解数学问题、感悟数学价值．

2 高中课堂数学抽象素养培养现状

通过查阅相关文献后发现，目前在高中课堂教学中有关数学抽象素养培养中存在许多不足之处，其中来自天水师范学院邵新颖[4]的一篇硕士论文的调查研究表明，在学习策略上，学生的逻辑思维能力比较薄弱，难以从数学情境中抽象概括出数学问题，导致在实际生活中运用数学解决问题的能力较低．在面对较为复杂的问题时，学生会缺乏自信心，久而久之，将会对数学产生抵触的情绪．江苏省平望中学一线教师仲一萍老师[5]提到，在教学策略上，教师对于新教材的理解过于片面，在教学中往往只注重教材上知识的传授，教学的内容没有层次性，没有考虑学生的认知发展规律，导致学生对数学内容的整合不明确，上课专注力难以长久保持，最终影响学生的学习效率．同时，教学过程中教师过于强调形式化的师生互动环节，忽视了对学生思维能力的培养，对于数学的本质要求没有落到实处．

数学抽象素养的培养对学生发展起着至关重要的作用，但在教学过程中往往被忽略.针对以上问题，本文将以“函数的导数”为例，探讨数学抽象素养在课堂教学中的培养策略．

3 课堂教学中数学抽象素养的培养策略

高中课堂教学中，教师需要灵活运用数学教材，通过一定的教学设计，落实数学抽象素养的培养策略．在教学过程中，要以学生为主体，改变其完成任务式的学习，与课堂融为一体．教师要采取一定的教学策略，培养学生的数学抽象素养.针对以上问题，本文将从课堂教学中的教与学两个方面，讨论数学抽象素养在课堂教学中的培养策略．

3.1 教学策略

为了实现高效的课堂教学，教师要在理解教学的基础上，结合情境，融合数学史，帮助学生掌握抽象概念；在理解技术的基础上，运用信息技术直观展示抽象内容；在理解数学的基础上，设计思维实验、变式训练，让学生感悟数学抽象的过程．

(1)创设问题情境，感知数学抽象的必要性

数学是高中学习生涯中最主要的科目之一，大多数学生对于数学的学习会存在学起来吃力、厌学这一系列问题，随着时间的推移，学生两极分化严重．产生这方面问题的因素最主要还是因为数学的本质具有抽象的特征．为此，教师在课堂教学中，需要引入情境性问题，结合生活实际来进行教学．

以选修2-2中导数概念内容为例，由于导数概念本身比较抽象，在实际教学中，教师不能直接给出定义，可以通过引入气球的膨胀率、高台跳水运动员跳水的平均速度及瞬时速度等生活实例，让学生体会极限的思想，最后再引导学生思考从平均变化率到瞬时变化率的过程，从原有的知识基础上抽象概括出导数的概念．其目的是让学生从情境中感受数学的本质，学会用数学眼光分析实际问题，并用数学语言描述解决问题．通过情境的引入，帮助学生理解掌握概念．

(2)融合数学史，了解数学抽象的价值

数学概念通常是比较抽象的，我们可以将数学史融入数学课堂中，不仅可以让学生更深刻体会数学的本质，了解内容的来源，还可以激发学生在学习过程中的兴趣，感悟数学的价值，更快地融入到课堂之中．

例如，在导数概念中，导数是微积分的核心概念之一，教师可以适当介绍一下微积分的发展历程，微积分的发明权导致英德两个国家的荣誉之争．通过对这一数学史的介绍，让学生感悟数学的魅力和文化价值，激发学生的兴趣，体会到教材上看似简单的公式、定理等都是一代代伟大数学家常年探索才得出来的.在这个过程中，要让学生明白创造、探索知识比接受、学习已有的知识更来之不易．通过数学史的引入，不仅可增加课堂的趣味性，而且通过渗透一定的数学思想，还可激励学生积极主动探索学习，培养学生的发散性思维.与此同时，将抽象的概念具象化，帮助学生理解掌握，间接地提升了学生的数学抽象素养．

(3)巧用信息技术，将数学抽象过程可视化

在传统的授课模式中，教师大多通过口述及板书传授知识，当面临比较抽象复杂的概念时，学生往往难以理解．在信息时代，教师可以借助多媒体辅助教学，化静态为动态，直观地给学生展示概念的形成，促进学生对知识的理解．

例如，在高中数学选修2-2中讲授导数的几何意义时，这一内容较为抽象，学生需要很强的空间想象力以及抽象概括的能力．此时借助多媒体进行教学，显示切线PA与割线PB(图1)．通过动画演示，当点B无限接近点P时，归纳总结出此时割线的斜率就是点P处切线的斜率(图2)．多媒体教学给予学生直观体验，让学生体会割线到切线的变化过程，感受它们的内在联系——某点附近的曲线在很小的范围内可被大致看成直线，且此曲线可以用过此点的切线近似代替.这就是以直代曲的思想方法．这一过程将抽象内容具体化，不仅避免了学生遇到抽象问题时产生的枯燥及厌学感，同时也使其抽象思维能力得到了锻炼．

图1 图2

(4)设计思维实验，经历数学抽象的过程

在教学中，教师可以通过设计一定的思维实验，借助活动帮助学生完成新旧知识之间的同化，将数学活动经验抽象成数学概念问题．在这个过程中，教师需要引导学生独立思考，促进学生将数学知识内化，发挥个体的主观能动性，培养学生抽象概括的能力，理清逻辑抽象概念．

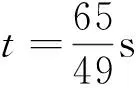
(5)利用变式训练，多方面体会数学抽象的结果

在教学过程中，教师可以采用一题多变的策略，从题中抽象出数学思想，引导学生从不同的视角看待问题，了解数学概念的本质，培养学生的数学抽象素养．

在求解导数切线方程问题时，学生容易将“过某点处的切线”与“在某点处的切线”混淆，难以区分．此时教师就需要采用适当的变式，让学生感悟两者间的不同．

例如，求曲线f(x)=x3-3x2+1在切点(1,-1)处的切线方程.

此类已知切点求切线方程的问题比较简单，大多数学生都能得到正确答案．通过对f(x)求导，再将切点代入，可以求出切线方程y=-3x+2．

变式1 求过曲线y=x3-2x上的点(1, -1)的切线方程.

学生若继续采用上述方法，就会掉入陷阱，算出错误答案．此题是“过”曲线的点，而不是“在”，所以并不代表此点就是切点．由此，不管此点是否在曲线上，都要先设出切点(x0,y0)，再利用条件求出切点，最后利用点斜式求出两个切线方程x-y-2=0或5x+4y-1=0．

变式2 已知曲线f(x)=x3-3x2+2x+a的一条切线方程为y=2x，求实数a的取值．

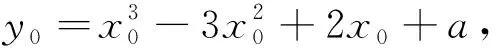
变式1的出现让学生明白处理已知点不在曲线上的问题时，要设出切点．变式2引入了参数a，从多种角度让学生感悟切线方程的题目．在经历了一定变式训练之后，学生才能切实明白概念之间的不同，避免解题时出现看得懂却做不来的问题．在教学中，教师通过题型的变化帮助学生理清问题的脉络，培养学生的发散思维，为提升学生的抽象思维奠定了基础．

3.2 学习策略

为了帮助学生提高学习效率，教师要在理解学生的基础上，培养学生敢于质疑、善于提问的学习方式，养成反思总结的学习习惯．

(1)敢于质疑，善于提问

由于个体差异，每位学生的认知程度与基础理论知识掌握得不尽相同，教师在上课的过程中不一定能全方位考虑到．学生在面对疑问时，要基于自己的想法多角度地思考分析问题，并敢于质疑、提出问题．

在导数概念的形成过程中，学生对于导数概念的理解存在一定的模糊性，多数学生对于变化率、平均变化率以及瞬时变化率之间的概念关系容易产生混淆，导致在实际运用的过程中错误地使用公式，影响计算结果．为了避免这类问题，学生需要总结，对于混淆不清楚的地方大胆向教师提问，理清平均变化率与瞬时变化率的计算方法以及概念的不同，最终明确导数的内涵．在提问的过程中，不仅可提高学生抽象概括的能力，还可培养学生的发散思维与创新思维．

关于导数概念的形成，教材通过创设运动员跳水比赛的情境引入，经历平均速度过渡到瞬时速度的过程，抽象概括出导数的概念．但实际结果是，学生并没有切实领会导数概念的本质，导致不能将其灵活地运用到实际应用题中．其主要原因就是在这个环节中，学生缺少了主动思考、主动提问的过程．在跳水问题中，学生可以结合实际情境提出问题，平均速度如何过渡到瞬时速度?如何将瞬时速度和导数概念相联系?通过问题串的形式强化对知识的掌握，最终加深学生对导数概念的理解，积累从具体到抽象的活动经验．

(2)自主归纳概括，构建认知结构

学生不仅仅要掌握教师所传授的知识，还要养成良好的学习习惯去主动学习．高中数学内容繁多，公式定理也很繁琐抽象．为了产生高效的学习，学生要学会将复杂抽象的知识简单化，自己总结归纳知识，构建框架．

例如，在导数及其应用这一章节学习结束时，大多数学生会混淆一些繁琐的知识点.此时学生需要总结，构建框架体系．在整理时，对于有关导数概念内容可将导数的定义，几何意义划分为一个小分支，将导数的运算分为基本初等函数及复合函数的求导运算，再将导数在函数中的应用、有关导数的单调性、极值与最值划分为另一个分支(图3)．通过框架示意图可以直观地展示这一章节的主要内容，帮助学生有效运用知识、掌握知识.这一过程使得数学内容变得有条理性，将某一系列的内容完整地呈现出来，将知识之间的逻辑性、抽象关系简单化，使得学习过程变得轻松．在整理的过程中也不断地在培养学生的发散思维，将零碎不足的知识系统化，提高学习效率，从而间接提高学生的数学抽象素养．

图3

4 结束语

数学抽象素养的培养对学生的数学学习具有重大的意义，不仅能加强学生对数学符号的敏感程度，还能激发学生对数学本质的探究，养成勤于反思的习惯．