一节概念课的教学实录与思考

佘 丹 (江苏省南京市中华中学 210006)

“代数式”(苏科版《义务教育教科书·数学》七年级上第三章第2节)是一节概念课，它是学生数学学习的一个生长节点，从这一节开始学生的学习由数到式，有了质的飞跃，同时它还起着统领全章的作用，因此对教师的教学提出了较大的挑战.笔者有幸参加了2019年江苏省南京市秦淮区教研室举办的青年教师课堂展示活动，现将自己的教学与思考与各位同行交流.

1 教学实录

1.1 梳理旧知

教师：在上课之前，老师想问大家一个问题，数学可以看作是研究什么的学科？

生(齐)：数.

师：研究它的什么东西？

生1：正数、负数、0、有理数、无理数.研究了数的分类.

生2：研究了数的定义.

生3：有理数的加减乘除，研究了数的运算.

师：(学生边说教师边板书，如图1)很好！关于数，我们研究了定义、分类、运算.

图1

设计意图让学生回顾数的研究方法，后续类比数的研究猜想代数式的研究方法，能够让学生掌握研究问题的一般方法，积累解决问题的经验.

1.2 创设情境

教师出示情境，与学生一起交流讨论.

情境1 如图2，这是用火柴棒搭小鱼的活动，前面已经研究过，从特殊推广到一般，搭n条小鱼需要多少根火柴棒？你有怎样的发现？试着填写下表，交流你的思考.

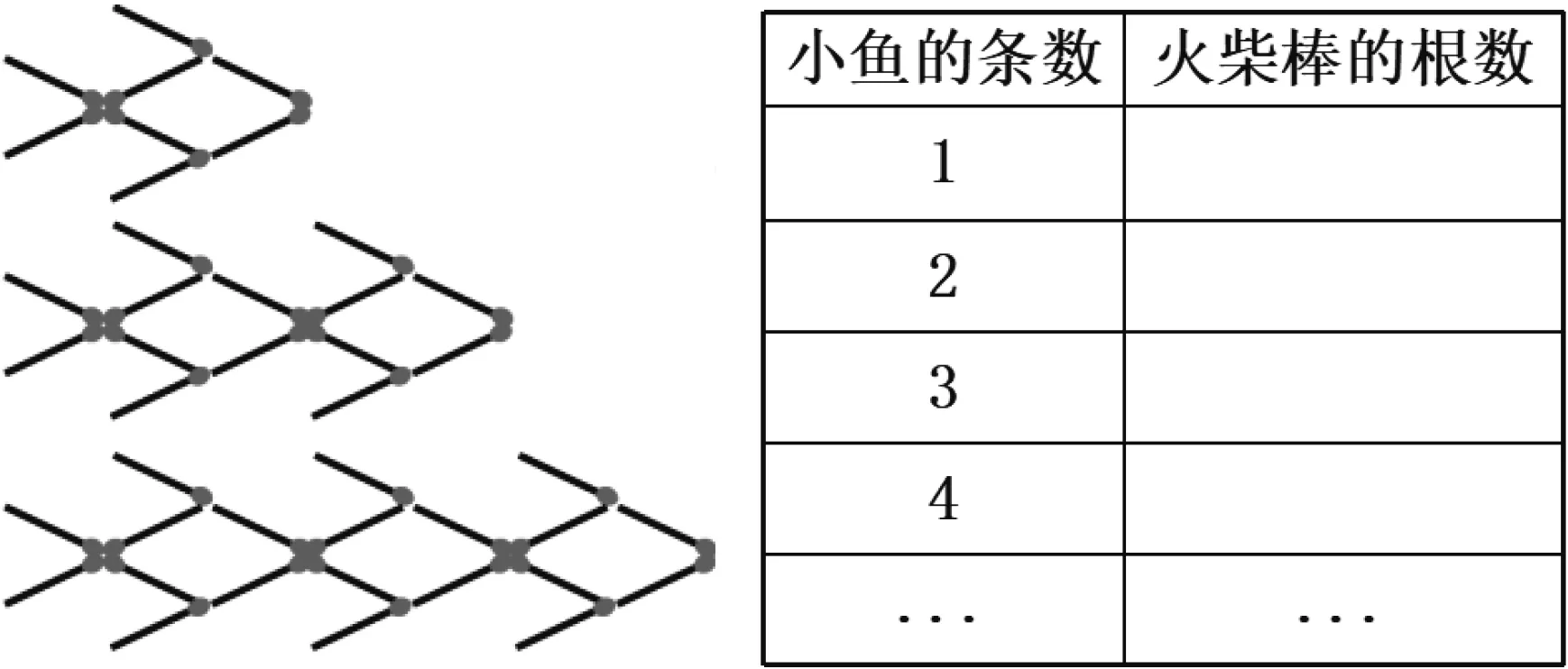
图2

生4：需要6n+2根火柴棒.

情境2 观察图3月历中右上角阴影方框中4个数，它们之间有怎样的关系？

图3

生5：每一列中，下面一个数比上面一个数大7.

生6：每一行中，后面一个数比前面一个数大1.

生7：在2×2方框中，对角线上数字之和相等.

师：很好！这个阴影框中4个数的关系对另外两个阴影方框也成立吗？对其他类似方框呢？

生(齐)：仍然成立.

师：像这样的方框中的4个数，他们两两之间都有关系，那如果我将其中一个数设为m，其他几个数是不是都可以表示出来了？比如设其中最小的一个数为m，则其他数为——

生8：m+1，m+7，m+8.

师：还可以怎么设？如果我以上方右侧的数为标准，设为m，则其他数为——

生9：m-1，m+6，m+7.

师：还可以怎么设？

生10：m-7，m-6，m，m+1.

生11：m-8，m-7，m-1，m.

师：看来，不管将哪一个量用字母来表示都是可以的，我们一般根据需要来选择.

情境3 某航空公司规定，乘坐经济舱的旅客每位可免费携带行李20 kg，超重部分每kg按票价的1.5%付行李费．随着机票价格和行李质量的变化，需付的行李费也将发生变化．

(1)从南京出发，携带行李30 kg乘飞机分别到达下列城市，应付行李费多少元？

(2)如果机票价格为m元，携带行李30 kg，应付行李费多少元？

(3)如果机票价格为m元，携带行李nkg(n>20)，应付行李费多少元？

师：请同学们读题目，分析你读出了哪些信息？

生12：每位可免费携带行李20 kg，行李费=超重部分×票价×1.5%.

师：第(1)问，携带行李30 kg乘飞机分别到达上述城市，应付行李费多少元？

生13：携带30 kg行李到达北京，行李费用为(30-20)×1 010×1.5%=151.5(元)；到达广州，行李费用为(30-20)×1 180×1.5%=177(元)……

师：非常好！找到数量关系之后，相应找到每个量并相乘即可，非常的清晰.看第(2)问，请你先观察，它和第(1)问有什么不同？从第(1)问到第(2)问是一个怎样的过程？

生14：第(1)问票价是具体的数字，第(2)问票价是用字母来表示的，这是从特殊推广到一般.

师：此时票价为——

生15：(30-20)×m×1.5%=0.015m(元).

师：更一般地，如果行李重量也一般化，又该如何？

生16：(n-20)×m×1.5%=0.015m(n-20)(元).

师：这里有个括号，为什么要加括号？如果把括号删掉呢，该怎么做？

生17：如果携带的行李小于等于20就没有行李费了.

师：怎么做才能把括号删掉呢？

生18：此时不知道n到底大不大于20，这要分类讨论，当n≤20时，0元；当n>20时，(n-20)×m×1.5%元；

情境4 某农场有亩产akg的水稻m亩，亩产bkg的水稻n亩，这个农场水稻的平均亩产为kg.

师：亩产是什么意思？

生19：亩产是指每一亩的产量.

师：要求的是什么？平均亩产怎么求？

生19：要求的是这个农场水稻的平均亩产量，平均亩产等于总产量÷亩数.

师：所以这个农场水稻的平均亩产为——

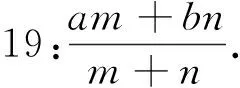
设计意图从实际问题中抽象出代数式，让学生感受到代数式就是一个从具体到抽象的数学建模过程；设计各种不同的代数式，帮助学生掌握代数式的特征．

1.3 建构概念

师：今天我们通过对实际问题进行分析，抽象出了这么多式子，我们把这样的式子称为代数式.那么它们具有怎样的特点呢？我们看下列式子.

试一试：下列各式中哪些是代数式？

(1)m+5； (2)a+b=b+a；(3)0；

(4)x2；(5)x+y>1； (6)abc；

生20：(2)(5)不是.

师：根据你的感觉，你觉得什么样的式子是代数式？

生21：不含“=”“>”.

生22：我觉得代数式含有字母、数字，还含有加、减、乘、除、乘方.

师：m和151.5是不是代数式？

生(齐)：是.

师：注意单独的一个数或字母也是代数式.

设计意图代数式是一个比较上位的概念，只观察代数式难以感悟代数式的共同特征，先让学生感受各种不同的代数式，然后根据自己的经验进行辨析，这个过程能让学生逐渐明晰代数式的特征，从而自主建构概念.

1.4 例题精练

教师出示例题，学生先动手做，再用希沃投影答案，并请学生逐个讲解.

(2)林老师用分期付款的方式购买汽车：首期付款a元，以后每月付款1 500元，直至付清欠款，x个月后，林老师共付款元.

(3)直角三角形两直角边长分别为acm、bcm，斜边长为5 cm,它的面积是cm2，斜边上的高是cm.

(4)一个两位数，个位数是x，十位数是y，这个两位数为，如果个位数字与十位数字对调，所得的两位数是.

师：请同学讲解第(1)题.

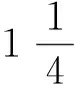
生(齐)：乘号.

生(齐)：加号.

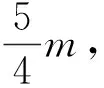
生24：首期付款a元，每月付1 500，x个月付1 500×x，一共a+1 500×x元.

师：非常好！那你看这个写法有没有问题？

生24：可以再简洁一点，直接写成a+ 1 500x元.

师：很好！数字与字母相乘时，乘号省略或者用小圆点表示，否则我们同学写的时候1 500×x，不知道这里是×还是x，所以直接省略(1 500x)或用小圆点表示(1 500·x)，并且把数字写在字母前面，而不能写成x1 500.还有要注意，如果这里是加减连接并且后面有单位，必须加括号，否则我们不知道元是1 500x的单位还是a+1 500x的单位.但是乘除要不要加括号，比如(1 500xy)元？不用，乘除我们已经默认它是一个整体了，就是这个整体的单位．再看第(3)题.

师：很好！同样注意写法，字母与字母相乘，乘号可以省略或者用小圆点表示.数字与数字相乘乘号可不可以省略？

生(齐)：不可以.

师：比如2×3，省略就变成23了，不行.可不可以用小圆点？

生(齐)：不行.

生26：十位数是y，就是10y,个位数是x，一共是10y+x，个位数字与十位数字对调，就是十位是x，是10x+y.

师：这里应该写成——

生26：乘号省略，10y+x和10x+y.

师：通过解决这道题，你有什么体会？我们在书写代数式的时候有什么要注意的？(学生说，教师板书.)

生27：数字与字母相乘，字母与字母相乘时，乘号省略或用小圆点代替；数字与字母相乘时，数字写在前面，字母写在后面；除法要写成分数线的形式；有加减且后面有单位时，代数式要加括号.

例2(1)一根弹簧长10 cm，每挂质量为 1 kg物体，弹簧伸长0.5 cm，则10+0.5x表示;

(2)说出右边代数式的意义：a+2b，2(a-b);

(3)你能选择其中一个代数式，说说它能表示什么实际意义吗？

(说明：例2由学生讲解，教师进行点评.)

设计意图因为例1主要让学生自己练，所以教师故意将学生不规范的书写呈现出来，然后再作强调，帮助学生规范书写并理解其中原由.例2让学生发现同一个代数式可以有不同的实际背景，有助于强化学生的符号感，为后继方程的教学作铺垫．

1.5 小结提升

师：通过这节课的学习，你有什么收获？

生29：我知道了代数式的定义，是用基本的运算符号(加、减、乘、除、乘方等)将数、表示数的字母连接起来的式子，并且单独的一个数或字母也是代数式.

生30：我知道了代数式的书写规范，数字与字母相乘，字母与字母相乘时，乘号省略或用小圆点代替；数字与字母相乘时，数字写在前面，字母写在后面；除法要写成分数线的形式；有加减且后面有单位时，代数式要加括号.

生31：同一个代数式可以有不同的实际意义.

师：到这里，老师又有个疑问了，这节课我们研究的还是数吗？

生(齐)：代数式.

师：因此，从这节课开始我们的学习有了一个质的飞跃，从数到式，这是一个从具体到抽象的过程.那么，类比数的研究，你觉得我们要研究代数式的哪些东西呢？

生(齐)：定义、分类、运算.

师：(教师板书，如图4)非常好，这一章我们将去研究这些问题.

图4

设计意图让学生对所学知识进行梳理、归纳和总结，类比数的研究方法猜想式的研究方法，体会类比的思想，学会研究问题的一般方法.

1.6 知识延伸

我们知道，按图2中方式，搭n条“小鱼”需要(6n+2)根火柴棒.

师：对于这个情境，你觉得还有哪些问题是我们未来要研究的？

提出问题，供学生课后思考探讨.

设计意图呼应开头，火柴棒搭小鱼的活动贯穿整个初中阶段，将代数式、方程、不等式、函数串联起来，形成一个体系，有助于学生掌握代数的知识体系.

2 教学思考

在进行了以上教学后，笔者从以下三个方面对本课进行了反思．

2.1 注重数学思想方法教学是培养学生能力的重要手段

数学知识是一个有联系的整体，特别是有些并列的数学知识，它们的研究方法相同，因而学习经验可被相互借鉴.本节课虽不是章节起始课，但对整个代数式的学习起着统领作用，让学生类比数的研究内容猜想代数式的研究内容，学生很快能够建构代数式的知识框架，这就学会了研究问题的方法．

2.2 自主建构知识是数学课堂教学的最高目标

数学活动是师生积极参与、交往互动、共同发展的过程，有效的教学活动是学生的学与教师的教的统一，学生是学习的主体，教师是学习的组织者、引导者、合作者[1]，只有学生自主建构知识，才能将其内化成自己的东西．本节课的教学中，代数式的概念不是直接告诉学生，而是在学生对代数式有一定感性经验的基础上，让学生凭经验辨析，体会什么样的式子是代数式，自主建构代数式的概念[2]．在代数式的书写规范上，允许学生犯错，然后通过启发和引导，促使其去思考和理解．

2.3 精讲精练是高效教学、训练思维的重要途径

数学的教学应激发学生兴趣，调动学生学习积极性，引发学生的数学思考，鼓励学生的创造性思维，形成核心素养．这需要教师打开学生的思考，以问题引领教学，避免“题海战术”．在本节课的教学中，问题情境中的四道题分别以表格、图形、文字的方式呈现，且涵盖各种代数式，在情景3的教学中，挖得比较深，引导学生思考每一问之间的关系，对于题目的条件(n>20)是否可以不要，如果不要又该如何，渗透了从特殊到一般的思想以及分类讨论的数学思想，并培养学生提出问题的能力．