模糊论辩框架的数学表示

王宗顺 吴家超

( 山东师范大学数学与统计学院, 250358，济南 )

1 引 言

形式论辩理论是涉及数学、计算机科学以及哲学等多门学科领域的研究主题.1995年，Dung[1]首次提出论辩框架(Argumentation Framework,AF)理论.该理论开创性的将论辩与逻辑编程、非单调推理等推理手段联系起来，形式论辩理论由此开始飞速发展.论辩框架理论作为形式论辩理论的一个重要概念，在非单调逻辑等研究中扮演着重要角色，目前已经成为了人工智能领域的一个重要话题.

在论辩框架的研究中，自然语言论辩情境中论证(Argument)的内部结构被忽略，仅保留论证间的冲突关系(通常称为攻击关系，attack relation between the arguments)，论辩情境被高度抽象化为一个数学模型，进而对建模后系统中的论证进行合理性的评估.在Dung的开创性工作后，论辩框架的各种扩展概念被相继提出，如偏好[2]，高阶攻击[3]，支撑关系[4]等.近年来，为了更好地刻画自然语言中的不确定性，添加数值的论辩框架逐渐吸引了更多的目光，如权重论辩框架，概率论辩框架，模糊论辩框架，权重双极论辩框架等等.在权重论辩框架中，Dunne等人[5]将攻击关系赋予数值来表示攻击的权重.在概率论辩框架中，Li等人[6]将概率分配给论证以及攻击关系来解释论辩框架中的不确定性，Hunter等人[7]对概率论辩框架进行了实例化建模.在模糊论辩框架中，Pereira等人[8-11]将模糊度与论证及攻击关系相结合来表示论证与攻击关系的信任度.在权重双极论辩框架中，Amgoud等人[12-14]将数值赋予论证来表示论证的信任度，并且加入了支撑关系.

本文主要关注的是模糊论辩框架.许多学者已经对模糊论辩框架做了深入的研究，本文将会对模糊论辩框架的数学形式进行一些讨论.首先，将会给出模糊论辩框架的两种数学定义，并且用模糊有向图和矩阵来表示有限论证的模糊论辩框架.然后，揭示这两种模糊论辩框架的数学表达形式与其它量化的不确定性论辩框架的联系.

2 模糊论辩框架的研究

目前，模糊论辩框架已经引起许多学者的关注.Pereira等人[8]提出了一种带有量化数值的论辩框架，其中论证被赋予实区间[0,1]上的模糊度来表示主体对于论证来源的信任度，但攻击关系仍为常规论辩框架下清晰的攻击关系.Janssen等人[10]提出了一种论证为常规论辩框架下清晰论证的模糊论辩框架，其中攻击关系被赋予实区间[0, 1]上的模糊度来表示主体对于攻击关系的信任度.Wu等人[11]提出了论证以及攻击关系均被赋予模糊度的模糊论辩框架，并且以模糊集的形式引入了外延语义.综合上述研究成果，本文将提出模糊论辩框架的两种数学表示形式，以便统一刻画各种赋予模糊度的论辩框架.

2.1模糊论辩框架的两种数学定义通过借鉴一些现有的关于论证或攻击关系与数值相结合的论辩框架理论的工作，本节将会提出模糊论辩框架的数学形式定义.为了不失一般性，把关注的重点放在论证以及攻击关系都被赋予模糊度的模糊论辩框架上.在给出模糊论辩框架的数学形式之前，首先简要介绍Dung的常规论辩框架的相关理论.

定义1一个论辩框架AF是一个二元组(Ar,Att)，其中，Ar是一组论证的集合，Att⊆Ar×Ar是一组论证间的二元攻击关系的集合.一个论证A攻击论证B当且仅当(A,B)∈Att.

Dung提出的经典论辩框架的数学模型是一个有向图，在这个有向图中，节点代表论证，箭头代表攻击关系.例如，Float模型AF=(Ar,Att)=({A,B,C,D},{(A,B),(B,A),(A,C),(B,C),(C,D)})可以由图1表示(红色字母代表论证，蓝色箭头代表论证间的攻击关系).

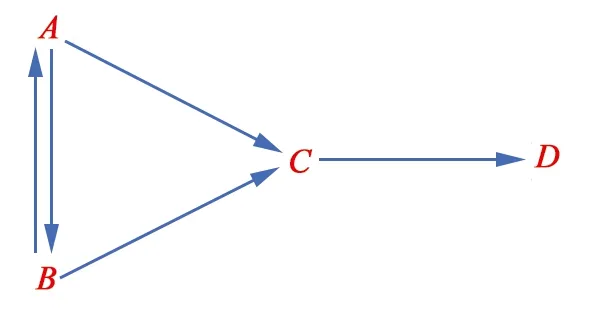
图1 Float模型

现在提出模糊论辩框架的两种数学定义形式.第一种形式是首先给定一个论辩框架，再将该框架中的每个论证以及攻击关系都赋予模糊度.这种定义方式是建立在常规论辩框架下的并且是易于理解的，具体如定义2所示.

定义2(第一种数学形式)给定Dung提出的论辩框架AF=(Ar,Att).FAF=〈A,ρ〉是AF上的模糊论辩框架，其中，A:Ar→[0, 1]是一组模糊论证的集合,ρ:Att→(0, 1]是攻击关系的模糊集.

模糊论辩框架的第二种数学形式不再局限于一个论辩框架内，而是对所有论证以及所有论证间的攻击关系都赋予信任度，即为每一个论证及攻击关系都赋予模糊度.这种定义方式在数学意义上更为严谨且合理，有着完整的模糊集的定义，具体如定义3所示.

定义3(第二种数学形式)任给一组论证Ar，模糊论辩框架是一个二元组FAF=〈A,ρ〉，其中，A:Ar→[0, 1]是论证的模糊集,ρ:Ar×Ar→[0, 1]是攻击关系的模糊集.

在提出模糊论辩框架的两种数学形式后，需要说明一下这两种数学形式之间的关系.虽然两种数学形式所构造成的模糊论辩框架从定义上看是存在差异的，但是这两种数学形式是可以相互表出的.下面的定理1证明了这两种数学定义方式是等价的，只是数学形式有所区别.

定理1定义2与定义3中的两种模糊论辩框架的数学形式可以相互表示，从而两种模糊辩论框架的数学表示形式是等价的.

证对于任意的符合定义3的模糊辩证框架FAF=〈A,ρ〉，其中，A:Ar→[0, 1]是模糊论证集,ρ:Ar×Ar→[0, 1]是攻击关系的模糊集，只要找到一个符合定义2的模糊论辩框架FAF′使得它与FAF完全等价，即可证明FAF可以由FAF′表出.首先取一个常规论辩框架AF=(Ar′,Att)，其中Ar′=Ar，Att={(A,B)|(A∈Ar)∧(B∈Ar)∧(ρ(A,B)≠0)}⊆Ar×Ar.简单来说就是把Att取作是FAF中的模糊攻击关系集ρ的支撑集.令AF上的模糊论辩框架FAF′=〈A′,ρ′〉，其中A′={(A,a)|A∈Ar∧a=A(A)}以及ρ′={((A,B),r)|(A,B)∈Att∧r=ρ(A,B)}.那么A′与A显然是完全相等的模糊集，而ρ′与ρ的支撑集中的元素的模糊度是完全相等的，而支撑集以外的论证的模糊度又是0，显然ρ′与ρ也是相等的.不难看出FAF′与FAF是等价的.

给定一个论辩框架AF=(Ar,Att)，对于任意的符合定义2的AF上的模糊辩证框架FAF=〈A,ρ〉，其中，A:Ar→[0, 1]是论证模糊集，ρ:Att→(0, 1]是攻击关系的模糊集.下面需要找到一个符合定义3的模糊论辩框架FAF′与FAF完全相等，为此令FAF′=〈A′,ρ′〉，其中，

A′={(A,a)|A∈Ar∧a=A(A)}，

(1)

ρ′={((A,B),r)|(A∈Ar)∧(B∈Ar)∧((A,B)∈Att⟹r=ρ(A,B))∧((A,B)∉Att⟹r=0)}.

(2)

那么A′与A显然是完全相等的模糊集，ρ′就是ρ的一个简单的扩张，并且加上了Att以外的那部分模糊度为0的攻击关系.所以FAF′与FAF是等价的.

综上所述，定义2与定义3中的两种模糊论辩框架的数学形式是等价的.

2.2用图和矩阵表示有限模糊论辩框架在实际应用中，论辩框架中论证的个数都是有限的.对于具有有限论证的模糊论辩框架，有着更形象的表达形式.在本节中，提供两种表示方法：一种是图示法，运用模糊有向图表示模糊论辩框架；另一种是利用矩阵表示，在后续的研究中，可应用矩阵的各种性质，丰富语义探讨的数学手段.

第一种表示有限模糊论辩框架的方法是常规的图示表示方法，称之为模糊论辩框架的模糊有向图.

定义4在模糊论辩框架模糊有向图中，图中的连接点代表论证，连接点的下标代表节点的模糊度，箭头代表攻击关系，箭头上方的数值代表该攻击关系的模糊度.

例1一个为Float模型赋予模糊度的模糊论辩框架FAF为

〈{(A,0.8),(B,0.7),(C,0.9),(D,0.8)},{((A,B),0.8),((B,A),0.7),((A,C),0.6),((B,C),0.6),((C,D),0.8)}〉，则该模糊论辩框架的模糊有向图如图2所示(红色部分代表模糊论证，蓝色箭头部分代表攻击关系)。

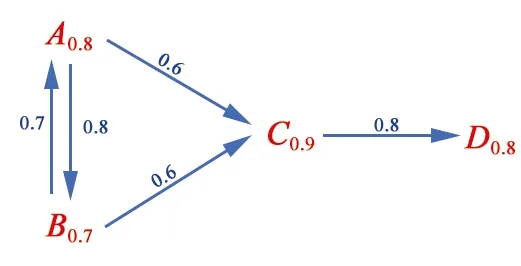
图2 模糊有向图下的Float模型

第二种表示有限模糊论辩框架的方法是矩阵的表示方法，称之为模糊论辩框架的矩阵.

定义5在模糊论辩框架的矩阵中，模糊论证被分别列在每行每列，矩阵的第i行第j列的元素表示第i行的论证对第j列的论证的攻击关系的模糊度.

以例1中的模糊论辩框架为例，该模糊论辩框架的矩阵表示如图3所示(红色部分代表论证，蓝色部分代表攻击关系).

图3 矩阵下的Float模型

矩阵的表示方法对于Janssen等人提出的模糊论辩框架更加有力，因为在这种框架中，可以舍去行列的论证，仅用一个矩阵就可以表示该论辩框架.

2.3相关的论辩框架与本文的两种数学形式之间的联系在已有的关于论辩框架理论的研究中，有许多理论与本文提出的模糊论辩框架的两种数学形式是相近的，并且可以用本文提出的两种数学形式进行表示.

Dunne等人[5]提出了给攻击关系赋予权重的权重论辩框架，其中论证是一般的清晰论证，而所有的攻击关系都被赋予一个(0,1]间的数值，具体如定义6所示.

定义6Dunne提出的权重论辩框架是一个三元组WAF=(Ar,Att,w)，其中(Ar,Att)是一个常规论辩框架，w:Att→(0, 1]是一个给攻击关系赋值的函数.

根据定义2，容易验证下述定理2成立.

定理2Dunne等人提出的权重论辩框架可以由定义2中的第一种数学形式刻画，只需要满足下述条件：

1) 对A进行限制，A:Ar→{0, 1}；

2)ρ:Att→(0, 1].

证对A进行限制以后，得到A:Ar→{0, 1}.可知该模糊集中的所有论证的模糊度都是0或1，这与经典集合理论中的元素是一致的，从而由模糊的转换成了清晰的.进一步由ρ:Att→(0, 1]可知所有的攻击关系都存在一个大于0的模糊度来表示其权重.因此本文提出的第一种数学形式可以用来刻画Dunne等人提出的权重论辩框架.

Pereira等人[8]提出了一种模糊论辩框架，其中论证的信任度由0到1之间的模糊度表示，也就是将常规论辩框架中的论证集替换为了模糊集A:Ar→[0, 1]，攻击关系为常规论辩框架下清晰的攻击关系.只需要将其攻击关系的模糊度限制到0与1两个元素上，Pereira等人提出的模糊论辩框架就可以看作是本文提出的模糊论辩框架攻击关系的模糊度恒为0或1的特殊情况.

根据定义3的数学形式，易证下述定理3成立.

定理3Pereira等人提出的模糊论辩框架可以由定义3中的数学形式刻画，只需要满足下述条件：

1) A:Ar→[0, 1]；

2) 对ρ进行限制，ρ:Ar×Ar→{0, 1}.

证对ρ进行限制以后，ρ:Ar×Ar→{0, 1}.可知该模糊集中的所有论证间的攻击关系的模糊度都是0或1，于是攻击关系就由模糊的转换为清晰的.因此本文提出的模糊论辩框架的第二种数学形式经过限制以后，其论证是量化的带有模糊度的，而攻击关系是清晰的，这与Pereira等人提出的模糊论辩框架是一致的.

在Janssen等人[10]提出的模糊论辩框架中，论证恒为常规论辩框架下的清晰论证，攻击关系被赋予实区间[0, 1]上的模糊度来表现攻击的强度，具体如定义7所示.

定义7Janssen等人提出的模糊论辩框架是一个二元组AF=(Ar,→)，其中，Ar是一组论证的集合，而→是Ar上的模糊攻击关系.

容易看出Janssen等人提出的模糊论辩框架是定义3中论证的模糊度恒为0或1的特殊情况.根据定义3，容易验证下述定理4成立.

定理4Janssen等人提出的模糊论辩框架可以由定义3中的第二种数学形式刻画，只需要满足下述条件：

1) 对A进行限制，A:Ar→{0, 1}；

2)ρ:Ar×Ar→[0, 1].

证对ρ进行限制以后，ρ:Ar×Ar→[0, 1].可知该模糊集中的所有论证的模糊度都是0或1，这与经典集合理论中的元素是一致的，于是论证就由模糊的转换为清晰的.因此本文提出的模糊论辩框架第二种数学形式经过限制以后，其论证是清晰的，而攻击关系是量化的带有模糊度的攻击关系，这与Janssen等人提出的模糊论辩框架是一致的.

实际上，进一步观察Dung提出的常规论辩框架，论证与攻击关系皆是清晰的.因此，若将本文提出的模糊论辩框架数学形式中的论证以及攻击关系的信任度都限制到0或者1，则Dung提出的常规论辩框架也可以由本文提出的数学形式所表达.

3 模糊论辩理论的研究进展

模糊论辩框架已经有诸多学者进行研究,在此指出本文的研究工作与前人相关工作的异同.在Pereira等人[8]提出的模糊论辩框架中，论证间的攻击关系是模糊的，但是论证是常规论辩框架下的清晰论证.在Janssen等人[10]提出的模糊论辩框架中，论证的信任度是模糊的，但是论证间的攻击关系是常规的清晰的攻击关系.另外，在Dunne等人[5]提出的权重论辩框架中，攻击关系带有大于0的权重，论证是常规的清晰的论证.定理2、定理3以及定理4表明了上述三种论辩框架都可以由本文提出的模糊论辩框架的数学形式表出.除此之外概率论辩框架[6]、哥德尔模糊论辩框架[11]等诸多具有不确定性的量化论辩框架都可以由本文提出的两种数学形式表出，证明过程都是类似的.

在上述数值和论证与攻击关系相结合的论辩框架中，一个重要的任务是对框架中的论证进行合理性的评估，也就是寻找框架中论证的合理性程度.这项工作的主要解决方法是论辩语义[15]，也就是寻求论证的合理性程度时所需要遵循的一些准则.目前已经有了一些相关工作.Janssen等人[10]以模糊论证所构成的模糊集的形式提出了模糊论辩框架的外延语义，包括可容许外延、优先外延、稳定外延.类似的，Wu等人[11]提出的模糊集的形式类似于Dung提出的外延语义，包括无冲突集、可容许集、完备外延、基础外延、优选外延、稳定外延.除此之外，Pereira等人[8]提出了模糊标签理论(Fuzzy-AF-Labelling).在该理论中，每一个论证都被赋予一个信任度作为可接受程度，并且可以通过一个迭代的算法求出论证的合理性可接受程度.另外，近些年来，Amgoud等人[12-14]在权重双极论辩框架中的工作也是具有突破性的，其模型与本文提出的模糊论辩框架基本一致，但是在权重图的基础上加入了支撑的工作，并且提出了语义所需要满足的基本公理，这也是模糊论辩框架的一个未来的研究方向.本文提出的论辩框架的两种数学形式是对已有模糊论辩框架相关工作的一个总结，为论辩语义学的进一步探讨奠定了数学基础.在将来可以沿着这两种数学形式来探索各种语义准则或者寻找新语义[15].

4 结 语

本文对于模糊论辩框架的数学形式进行了一些探讨.对于论证以及攻击关系都被赋予信任度的模糊论辩框架，提出了两种数学表达形式：一种具有严格的数学定义，是对系统中的所有论证及攻击关系赋予信任度；另一种更为直观，是对常规的论辩框架中的论证及攻击关系赋予信任度.对具有有限论证的模糊论辩框架，给出了模糊有向图和矩阵的数学表示方法.另外，还进一步说明了这两种模糊论辩框架的数学形式与现有的其他不确定性论辩框架之间的联系，证明了Pereira等人提出的模糊论辩框架，Janssen等人提出的模糊论辩框架以及Dunne等人提出的权重论辩框架都可以看作是本文提出的模糊论辩框架的特殊形式，都可以利用定义2或定义3来表示.

在未来的研究中，将会利用这两种数学形式来探讨模糊论辩框架的论辩语义，包括外延语义以及标签语义.另外比较重要的工作是如何利用现实的信息来构造模糊论辩框架，因为只有实现模糊论辩框架的实例化建构才能将人类推理与模糊论辩框架推理工作联系起来，才能充分发挥模糊论辩框架的推理作用.