基于小波框架的稀疏正则化方法及其在图像复原中的应用

袁存林 宋义壮

( 山东师范大学数学与统计学院，250358，济南 )

1 引 言

实际获取的图像总是受到模糊和噪声的干扰，这种干扰降低了图像的质量. 因此，直接从成像设备中得到的图像总是为退化图像. 在一些诸如医学成像的领域中，这种退化图像会影响医生的诊断，甚至可能会导致误诊而引起医疗事故.因此，从含有模糊和噪声的退化图像中复原原始图像有着重要的应用价值.

记u∈Rm1×m2为原始图像，观测的低质量图像f∈Rm1×m2由图像u受模糊和噪声的干扰而形成.在数学上，图像复原可表示为以下问题的反问题：

f=Au+η,

(1)

其中η为高斯白噪声，A为与模糊算子对应的矩阵.

本文旨在从观测图像f重建高分辨率图像u，该问题可通过求解问题(1)的最小二乘问题

(2)

来求解.问题(2)通过变分法可以转化为

ATAu=ATf.

(3)

而矩阵ATA是病态的，其最小特征值在零附近，在受噪声干扰的情况下，直接求解(3)式会放大噪声.

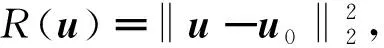
(4)

其中，第一项为保真项，第二项为正则化项，权重参数λ>0.这是一个N-P难问题.

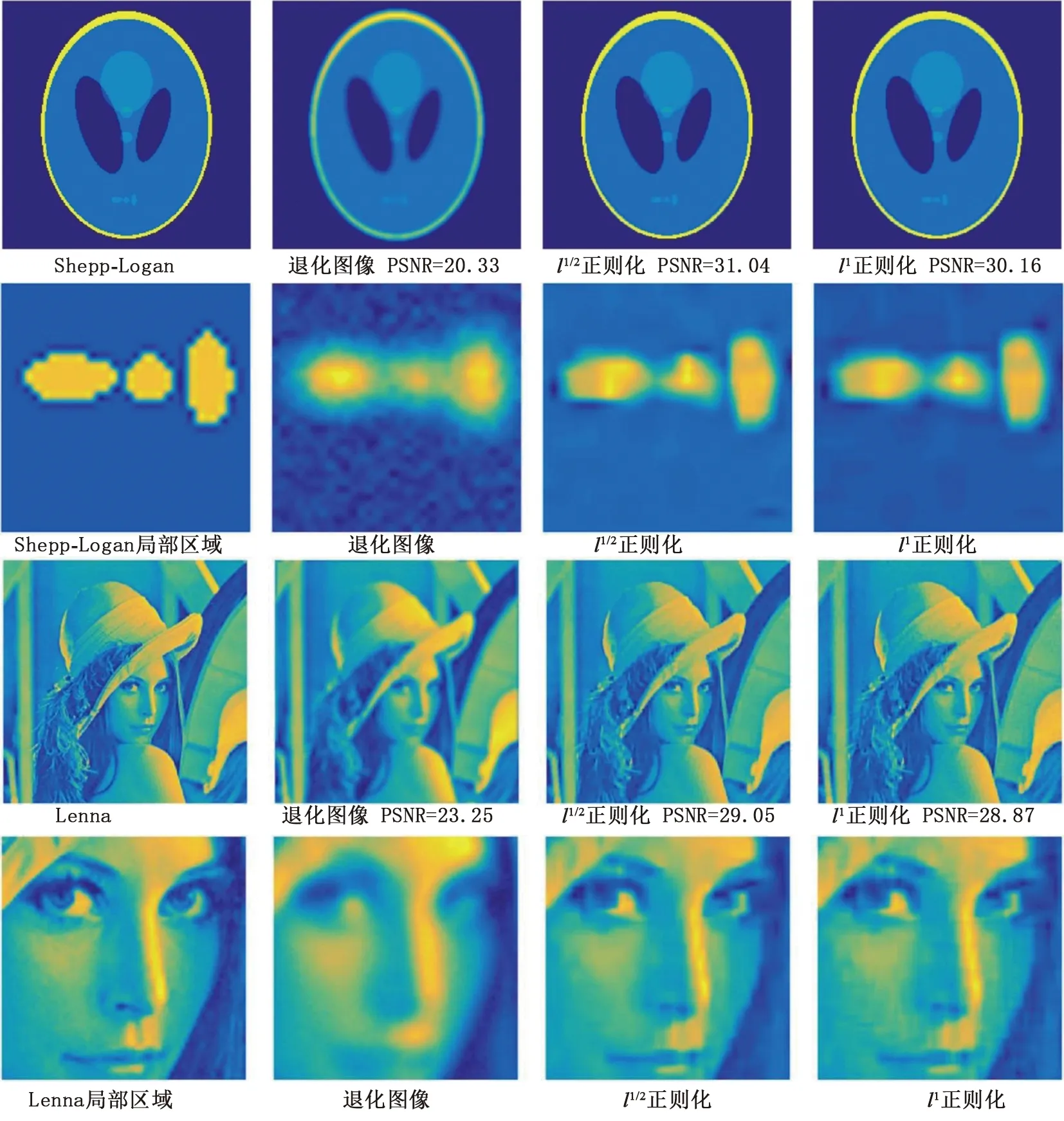
使用l1或lq(0

(5)

小波框架变换W一般可表示为以下形式：

(6)

图像u在小波框架下分解，得到系数Wαu，其中α∈Λ={(α1,α2)∈Z2|0≤α1,α2≤r}.当α=0时，W0,0u为稠密系数，它刻画了图像的全局特征，即每个像素取为局部像素的加权平均；当α≠0时，由于Wαu中大部分元素为零或集中在零附近，称Wαu为稀疏系数，它刻画了图像的局部特征，即图像的奇点或细节特征，比如边缘和隐式边缘.系数大部分为零或集中在零附近的现象称为稀疏性.模型(5)中参数γ的选取需要反映系数Wu的稀疏性，在本文中，当α=(0, 0)时，Wαu为刻画图像全局特征的稠密系数，取γ[α]=0;当α≠(0, 0)时，Wαu为刻画图像局部特征的稀疏系数，取γ[α]=1.

下面将使用交替方向乘子法(Alternating Direction Method of Multipliers，ADMM)[7]求解模型(5).

2 模型求解

对于小波框架模型(5)，取d=Wu，则模型(5)可转化为具有约束条件的极小化问题：

(7)

问题(7)的增广拉格朗日函数为

(8)

其中y称为拉格朗日乘子，ρ>0为惩罚参数.对(8)式适当变形有

(9)

极小化问题(9)的ADMM型算法(算法1)如下：

(10)

(11)

yn+1=yn+ρ0(Wun-dn),

(12)

ρn+1=ρn·C.

(13)

其中，初始参数ρ0>0，常数C>1，y0,d-1为给定初值. 在上述算法1中，第1步与第2步相当于交替更新变量u,d求Lρn(u,d,yn)的最小值解，第3步使用梯度上升法不断更新拉格朗日乘子y，第4步使参数ρ趋于无穷以保证算法的稳定性，这一点将在数值实验中体现.

对(10)式右端求Fréchet导数，并令左端为零，可得

(14)

由d=Wu及(6)式中W的定义，可知dα=Wαu，其中α∈Λ.故而(11)式可写为以下形式：

(15)

当α=(0, 0)时，由于γ[α]=0，可得

(16)

当α≠(0,0)时，γ[α]=1，对(15)式使用半阈值公式[5]求解可得

(17)

(18)

接下来将给出图像恢复领域常用的基于小波框架的l1正则化模型[6]，用以衡量小波框架下l1/2正则化模型(5)对图像的恢复效果.小波框架下l1正则化模型如下：

(19)

求解模型(19)的ADMM算法(算法2)如下：

(20)

(21)

yn+1=yn+ρ0(Wun-dn).

(22)

(20)式可通过求Fréchet导数求解，(21)式可使用软阈值公式求解. 在接下来的数值实验中，将对比算法1和算法2对图像的恢复效果，以验证小波框架下l1/2正则化方法的可行性.

3 数值实验

首先介绍一下数值实验中使用的小波框架和衡量图像恢复效果的标准. 小波框架使用B样条紧小波框架[6]，在一维情况下，有滤波器

二维情况下的滤波器qα可通过一维情况下的滤波器做张量积得到qα[k1,k2]=qα1[k1]qα2[k2]. 小波框架变换Wα作用于图像u相当于滤波器qα与图像u做卷积：Wαu=qα[-·]*u，*为循环卷积. 图像的恢复效果通过峰值信噪比(Peak Signal to Noise Ratio，PSNR)衡量，峰值信噪比PSNR定义如下：

PSNR=10×log10((max(u))2/MSE),

接下来将探究l1/2、l1两种正则化方法对图像的恢复效果. 四幅测试图像分别为Shepp-Logan、Cameraman、Lenna和Fingerprint(图1)，图像大小均为256×256，对其施加模糊核大小为7×7且标准差为4的高斯模糊以及40 dB的高斯白噪声.

图1 测试所用图像

由表1可以看出，四幅图像使用l1/2正则化方法所耗用的时间均低于使用l1正则化方法. 在恢复效果上，Fingerprint图像使用l1正则化方法的恢复效果略好一些，Shepp-Logan、Cameraman和Lenna三幅图像使用l1/2正则化方法的恢复效果较好，且Shepp-Logan图像使用l1/2正则化方法有着较大的优势, 这种现象可能与图像的稀疏程度有关. 文献[8]使用图像的梯度特征衡量其稀疏程度，考虑到小波框架下滤波器可以沿不同方向捕获图像的各类型局部特征，在本文中，使用稀疏度S(u)衡量图像u的稀疏程度，S(u)定义如下：

表1 小波框架下l1/2、l1正则化方法的恢复效果(PSNR值)及耗用时间

其中m1×m2为图像像素的总个数，指标集K={(i,j)∈Z2|0≤i,j≤r,i2+j2≠0}，(r+1)2-1为集合K中元素的个数，Γ(Wαu)为Wαu中绝对值小于或等于1的元素总个数(图像像素值在0到255之间).通过上述定义可知，稀疏度S(u)衡量了图像u在变换域中系数的稀疏程度，S(u)越大，说明变换域中的系数越稀疏.为衡量两种正则化方法间的相对恢复效果，定义某图像l1/2的离差为使用l1/2正则化方法恢复的PSNR值与使用两种正则化方法得到的PSNR均值之间的差，类似可定义l1的离差. 离差越大，表示该正则化方法的相对恢复效果越好.

表2给出了各图像的稀疏度及l1/2、l1的离差，并通过图2展示了l1/2、l1的离差随着图像稀疏度的变化趋势. 通过表2和图2可以发现，图像的稀疏度和l1/2的离差呈现出正相关性，即随着稀疏度的增加，l1/2正则化方法的恢复效果(PSNR值)逐渐超越l1的恢复效果，并且优势越来越大.l1的离差和图像的稀疏度呈现出负相关性，对于稀疏度低的图像，l1正则化方法具有一定的优势. 从而可以根据图像稀疏度这一先验信息，选择合适的正则化方法进行图像恢复：对于稀疏度低的图像，选择l1正则化方法更合适；对于稀疏度高的图像，选择l1/2正则化方法更合适.

表2 各图像的稀疏度及在不同正则化方法下的离差

图2 稀疏度与离差关系图

图3给出了Shepp-Logan和Lenna图像在两种正则化方法下的恢复图像. 为了进一步对比小细节的恢复效果，本文对Shepp-Logan和Lenna图像的局部区域进行放大(图3第2排和第4排). 可以看出，对于Shepp-Logan图像的细节特征，l1/2正则化方法能更好地兼顾降噪和去模糊，局部图案的去模糊效果更好一些，图案以外区域降噪效果更明显；对于Lenna图像，l1/2正则化方法对其脸部轮廓的恢复效果更好. 鉴于l1/2正则化方法在恢复图像细节特征方面的表现，对于小细节要求较高的图像恢复工作，l1/2正则化方法是一个可行的选择. 对于实验中使用的数据，C取为2，初值y0,d-1为零，求解l1/2、l1正则化模型的两种算法的迭代次数分别为20与100. 不同图像使用的参数λ,ρ0在表3中给出.

图3 恢复图像对比图

表3 不同图像使用的初始参数λ,ρ0

最后，为了验证求解l1/2正则化模型的算法1的稳定性，定义误差Ek+1=‖uk-u‖2/‖u‖2，uk由算法1在第k+1次迭代时生成，k≥0，u为真实图像.图4展示了误差随迭代次数的变化趋势，可以看出，随着迭代次数的增加，误差不断减小，并逐渐达到稳定状态，从而证实了算法1的稳定性.

图4 误差随迭代次数的变化趋势

由实验可知，在小波框架下，用以求解l1/2正则化模型的算法是稳定的.同时，l1/2和l1两种正则化方法之间的相对恢复效果和图像在小波变换域中系数的稀疏程度呈现出明显的相关性：图像在小波变换域中的系数越稀疏，l1/2正则化方法的相对恢复效果越好.对于图像中受干扰的细节特征，l1/2正则化方法相比于l1正则化方法能够更好地兼顾降噪和去模糊，从而更好地恢复图像的细节特征.