多跨距无刷双馈电机转子绕组设计及特性分析

戈宝军，牛焕然，林鹏，肖芳，毛博，温亚垒

(哈尔滨理工大学 电气与电子工程学院，哈尔滨 150080)

0 引 言

无刷双馈电机(brushless doubly-fed machine，BDFM)是一种新型结构的的感应电机，其定子有两套不同极对数的绕组组成，同时具有同步电机和感应电机的运行特点。定子功率绕组直接与电网相连，承担电机的主要功率部分，定子控制绕组通过变频器与电网相连，其中控制绕组电压较低，主要承担电机的转差功率，其功率较小，所需的变频器容量也较小[1-2]，特别是在高电压等级场合，较小的变频器容量，可以有效地降低调速系统的成本，作为传统有刷双馈电机的取代方案，无刷双馈电机在风能发电和高压电机领域具有良好的应用前景。

为提升无刷双馈电机的性能，国内外学者做了大量的研究工作，文献[3]给出了一种双正弦的转子绕组设计方法，并设计了一台64 kW的样机，分析了电机带载情况下电机谐波磁势及整机效率的问题。文献[4]给出了一种加导磁条的新型转子结构，并对比分析了不同转子结构对无刷双馈电机不同工况下的性能影响；文献[5]基于齿谐波和双正弦原理给出了一种等跨距不等匝的双层绕组设计方法，并对比分析了不同结构的转子谐波磁动势问题。本文提出了一种多跨距不等匝多层绕组的设计方法，这种绕组设计方法能够针对指定次谐波进行线圈匝数和跨距的灵活选取，可以有效地提高转子绕组导体利用率，削弱整机谐波含量。

无刷双馈电机具有良好性能的关键在于转子，转子的结构好坏直接影响了电机的整体性能，因此，对于无刷双馈电机转子设计研究至关重要，本文基于磁阻与绕线混合式转子结构提出了一种新型转子绕组设计方法，并结合具体示例对于多跨距复合式绕组的原理及设计原则进行了详细的说明，最后给出了一套低谐波的无刷双馈电机转子绕组设计方案。并通过建立Maxwell 2D有限元模型，对多跨距混合式转子的无刷双馈电机和普通双正弦转子的无刷双馈电机进行了相关的对比分析。

1 BDFM基本结构及运行原理

无刷双馈电机相对于传统的有刷双馈电机在于其定子由两套不同极对数的绕组组成，两套不同极对数的绕组之间不能直接进行能量传递，须通过转子实现间接的能量传递，这就要求无刷双馈电机的转子能够同时调制出两种不同极对数的旋转磁场，这对于转子的性能要求较高，同时也限制了无刷双馈电机的发展，目前对于无刷双馈电机的研究还处于实验室测试阶段，还未进入规模化的工程性应用。

无刷双馈电机双馈运行时，定子两套绕组将同时产生两个不同的旋转磁场，两套旋转磁场的方向与定子和电网的联接方式有关。当功率绕组和控制绕组均正相序与电网相连时，两套旋转磁场的旋转方向一致，此时电机处于超同步运行状态；当功率绕组和控制绕组分别以正相序和反相序与电网相连时，两套旋转磁场旋转方向相反，此时电机处于亚同步运行状态。

对于功率绕组极对数为pp，频率为fc；控制绕组极对数为pc，频率为fc的无刷双馈电机，当功率绕组直接与电网相连，控制绕组通过变频器与电网相连，电机实现双馈运行时，电机转速为

(1)

其中:“+”表示控制绕组产生的磁场旋转方向和功率绕组产生的磁场旋转方向相同，此时电机处于超同步运行状态；“-”表示定子两套绕组产生的旋转磁场方向相反，此时电机处于亚同步运行状态；当fc=0时，即电机控制绕组接入直流电时，电机处于同步运行状态。

2 双正弦绕组及多跨距复合式绕组

2.1 基于齿谐波的双正弦绕组原理

根据交流电机绕组理论，对于极对数为p，槽数为Q的m相对称转子绕组，转子中除了产生极对数为p的基波磁动势外，还会产生极对数为v=2mq±1的齿谐波磁动势,其绕组系数与基波绕组系数相等。同时基于齿谐波原理的多相转子绕组可以通过归算为三相绕组进行计算，归算后的三相转子绕组v对极谐波磁动势可以表示为：

(2)

式中Fφv为v对极谐波磁动势幅值。

根据电机学原理可知，转子绕组归算后的三相合成磁动势表达式为

(3)

当v=2mq+1时，三相合成的磁动势表达式为

(4)

同理，当v=2mq-1时，三相合成的磁动势表达式为

(5)

通过式(3)、式(4)和式(5)可知，齿谐波绕组中v=2mq+1次谐波磁动势和v=2mq-1次谐波磁动势旋转方向相反。

无刷双馈电机要求转子能够同时产生两种不同极对数的磁动势，并且旋转方向相反，根据上述理论，基于齿谐波原理设计的转子绕组能够满足无刷双馈电机转子同时产生两种主要基波磁动势的要求。

基于齿谐波原理设计的转子绕组，如果转子槽数仅选择Q=pp+pc时，由上述分析可知，其高次齿谐波磁动势与基波相当，电机整体谐波较大，电机不具备实用性。依据电机学原理可以对转子槽数进行适当的扩展使其既可满足齿谐波原理，又能兼顾削弱其他次谐波的要求，根据上述理论扩展后转子槽数需满足

Z2=k(pp+pc)。

(6)

式中：Z2为扩展后转子槽数；k为正整数。

基于齿谐波原理设计的正弦绕组为使气隙磁动势接近正弦，转子槽导体数采用正弦规律排布，即每相导体数分布规律为中间槽号导体多，两侧槽号导体少，这种特殊的导体分布规律可以使电机气隙磁动势趋近于正弦，对于电机内谐波有较好的抑制作用，但其对线圈匝数依赖较大，对于转子匝数较少的电机来说，其正弦排布规律优势不明显。

2.2 多跨距复合式绕组

文献[3]给出的双正弦转子绕组设计方案对于大功率电机及转子绕组匝数较小的电机来说优势并不明显，对与主要基波极对数相近的谐波抑制能力有限。且基于文献[3]设计的转子绕组，转子每相相邻槽号匝数不等，电机制造过程中绕组嵌线工艺较为复杂。

针对正弦绕组每相各槽号不等匝线圈设计带来的电机下线工艺复杂，以及对于大功率电机转子匝数较少，匝数按正弦规律排布时与基波极对数相近的齿谐波削弱效果不明显的问题，对基于齿谐波的正弦绕组进行了改进。提出了一种具有多种跨距的复合式绕组结构，其具体排布如图1所示。

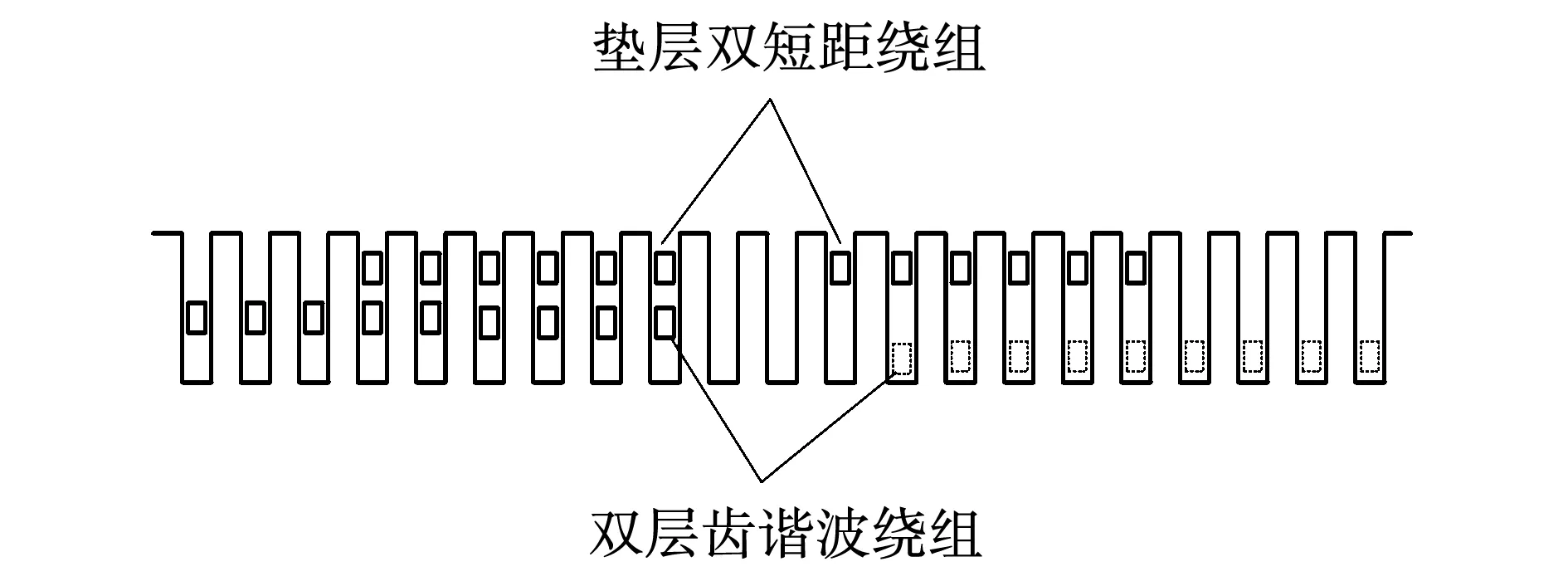
图1 转子槽导体分布图Fig.1 Distribution of conductors in rotor grooves

如图1所示的转子绕组共分为三层，转子槽底部的两层线圈按上节所述的齿谐波绕组原理正常排布，其与正弦绕组区别是底部的双层齿谐波绕组为等匝等距排布，位于转子槽顶部的单层绕组的跨距和匝数均与下层的齿谐波绕组不相等，每相不同层的线圈依次串联。这种绕组排布方式不仅能够起到不等匝绕组对谐波的抑制效果，还在一定程度上简化了绕组的下线工艺难度。

单层双短距绕组能够做到一套绕组同时具有两种跨距，根据交流电机绕组理论其同时具有两种短距系数，根据合理设计能够同时削弱多种不同的谐波。其设计原则为：

1)将转子槽数缩小为原先的一倍，将两种跨距的绕组分别按普通三相绕组单独排布，由于基于齿谐波绕组的无刷双馈电机转子绕组不具备固定的极对数，基于单层双短距设计的绕组可以摆脱单层绕组对线圈跨距的限制，可以根据需要合理的选取合适的跨距。

2)将两套绕组分别排布在奇数槽和偶数槽内，两套绕组之间的相对位置可以根据需要灵活调节。

3)可以根据需要将两套不同跨距的绕组采用顺接或反接串联起来。

将齿谐波绕组和单层双短距每相依次串联在一起，便组成了多跨距复合式转子绕组。这时除了原来的每套绕组中存在的短距线圈作用之外，还增加了一个由于不同绕组之间的空间相位差引起的短距效应，可以同时用来削弱多个谐波，进而显著地降低了电机谐波磁势含量，多跨距复合式转子绕组其中一相具体排布如图2所示。

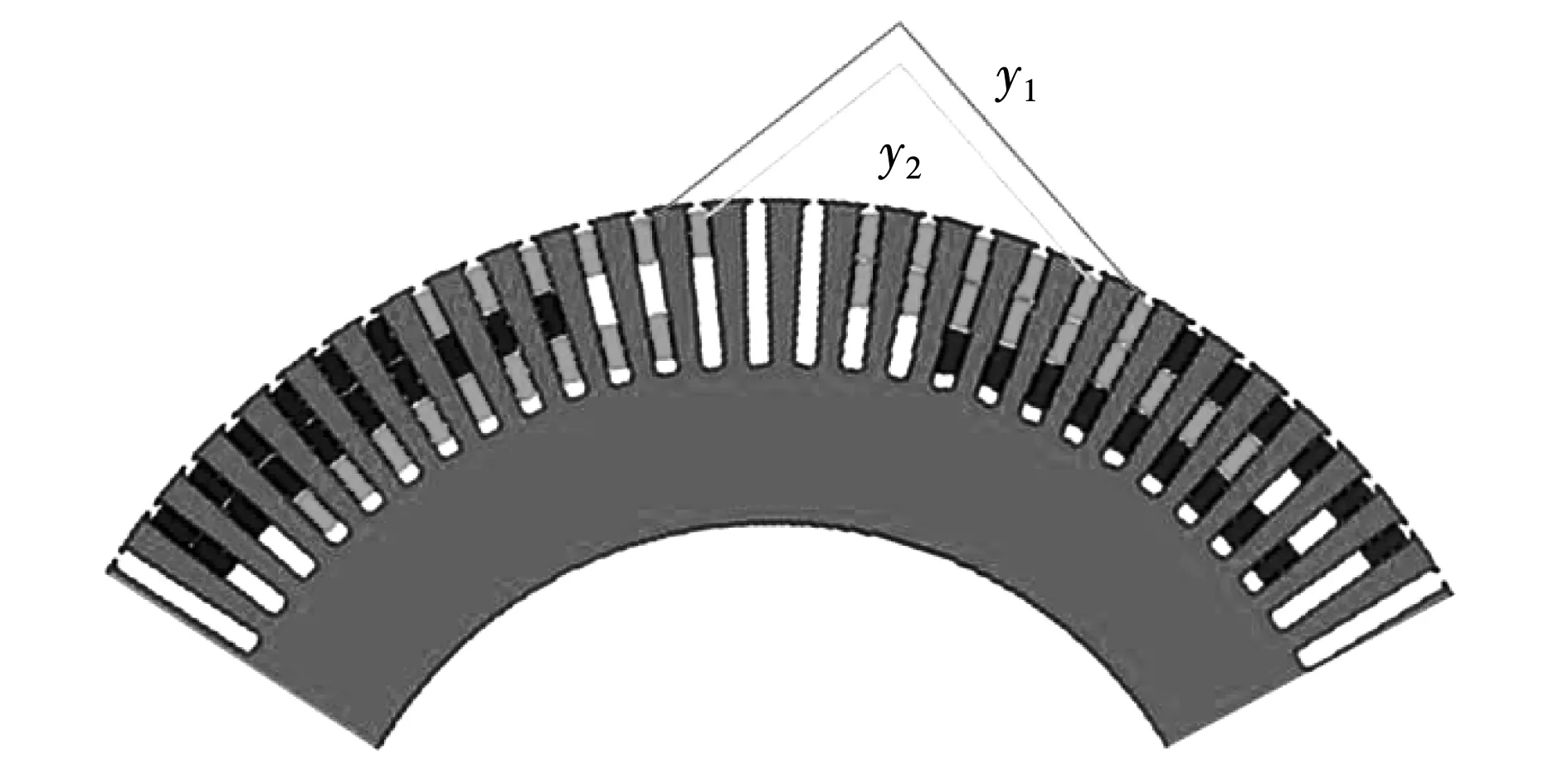
图2 多跨距绕组单相分布示意图Fig.2 Schematic diagram of multi-span winding distribution

如图2所示的不同跨距的线圈在转子槽的连接图，每相绕组由3种不同跨距的线圈组成，每相不同层线圈沿中心线对称分布，每种跨距线圈导体数相同，每相不同跨距线圈之间可以根据需要采用顺接串联或反接串联，对于多层线圈等匝数组成的复合式多跨距转子绕组，能够起到使电机磁动势趋近正弦的目的，同时对于与基波极对数相近的谐波有明显的削弱作用。

2.3 转子绕组谐波磁动势分析

常规电机绕组大多采用等匝线圈绕制，因此基于传统的电机绕组磁动势及绕组系数的计算方法并不适用于非常规线圈绕组，在基于常规计算绕组分布系数的基础上给出了适用于多种线圈的绕组分布系数计算方法。

假设转子绕组第m相第j槽包含的导体数为Nj，在不考虑槽口系数的条件下，则第j(j=1，2，3，…，q)个线圈的v次合成磁动势可表示为

(7)

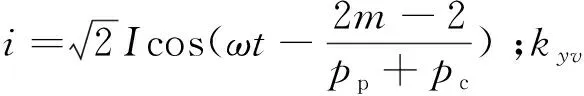
对于转子绕组第m相实际选用的q个线圈组，v次谐波合成磁动势为

(8)

第m相实际选用的q个线圈组，v次谐波合成磁动势的矢量和可表示为

(9)

则转子绕组第m相实际选用的q个线圈组v对极下的分布系数可以表示为

(10)

同时由于转子绕组每相的连接方式相同，即转子绕组每相的绕组分布系数均相等，即kqmv=kqv。

则其绕组系数可以表示为

kωv=kqvkyv。

(11)

其中绕组短距系数kyv的计算方法参阅了文献[7]中多跨距线圈的计算方法，其详细推导过程不再赘述。

3 多跨距复合式绕组设计示例

依据上述理论分析，结合具体示例阐述基于混合式转子的多跨距复合式转子绕组的设计方法，选取一台功率绕组极对数pp=2，控制绕组极对数pc=4，定子槽Z1=72，转子槽Z2=84的无刷双馈电机为例，转子绕组相数m=pp+pc=6，由扩展后转子槽数为84，可知，转子槽可以划分为6组，每相最大转子槽数为14。

为消除转子不等节距绕组需要若干特殊跨接线的突出缺点，转子绕组采用部分空槽设计方案，并将转子结构设计成外反应式磁阻转子与绕线转子相结合的新型混合式转子结构，其转子结构如图3所示，该混合式转子的直轴数为n=pp+pc，即控制绕组和功率绕组极对数之和，即定子绕组极对数为2/4的无刷双馈电机直轴数为6。

转子绕组方案，由于转子结构采用磁阻和绕线的混合式结构，转子虚拟槽数为84槽，实际槽数为72槽，其每相具体槽号分布如图3和图4所示。

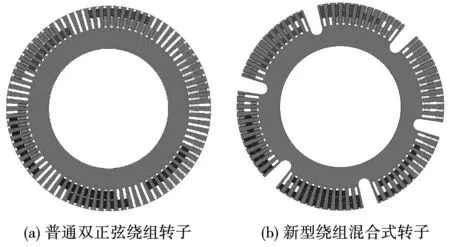
图3 不同转子绕组结构电机模型Fig.3 Motor models with different rotor windings

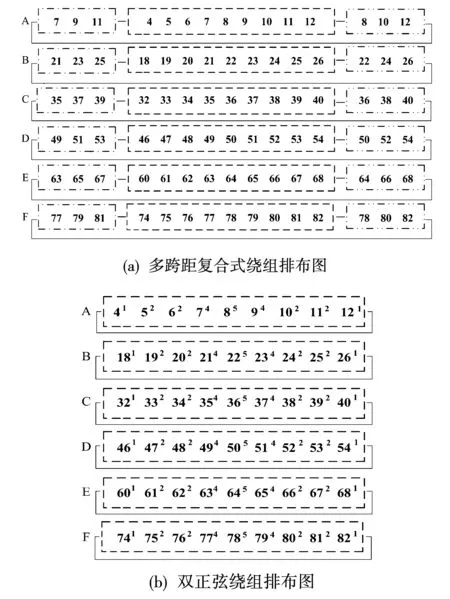
图4 不同绕组结构排布图Fig.4 Layout diagram of different windings

由于基于齿谐波原理设计的转子槽扩展后会导致基波绕组系数降低，为提高绕组系数，通常选用舍弃部分槽号的设计方法，丢弃某些边缘槽号后，部分绕组磁动势会相互抵消[11]，因此，为了提高导体利用率及综合绕组系数，每相选用连续的9个槽号,其中单层双跨距绕组槽号选取原则为，确保其上下层边和双层齿谐波绕组沿中心线对称分布时合理的选取跨距和槽号，奇数槽和偶数槽在电机转子槽中的分布如图3所示。

依据上述原理，设计的无刷双馈电机转子绕组如图4(a)所示，包括6个自闭合回路，其中A和D，B和E，C和F同相位，其中图4(a)中虚线内双层齿谐波绕组跨距为12，每槽线圈数为5。单层双短距绕组部分，点划线内跨距为9，线圈匝数为2，双点划线内跨距为7，线圈匝数为2，这3种跨距线圈依次顺接串联后再做短路连接。

双正弦绕组具体排布如图4(b)所示，图中上标表示匝数，每槽线圈匝数依次为1,2,2,4,5,4,2,2,1按照正弦规律排布，每相选用连续的9个槽号然后自闭合短路连接。

其中双正弦不等匝绕组匝数计算参阅了文献[3]和文献[5]的设计方法，多跨距复合式绕组匝数配合参阅了文献[7]低谐波非等元件匝数计算方法，详细推导过程本文不再赘述，其具体分布如图4所示。

为验证多跨距复合式绕组的谐波特性，将如图4(b)所示的双正弦绕组作为对比，在保证两套绕组匝数槽号相等的条件下，结合前节给出的多跨距绕组磁动势分析方法，以控制绕组4对极的基波磁动势为基准波，则转子多相合成的v对极谐波磁动势相对于基准波的磁动势比值为

(12)

式中：F1表示基准波的磁动势；Fvp表示v对极谐波的磁动势。

绕组各次谐波磁动势百分比含量及绕组系数分析结果如表1所示，其中合成磁势百分比中相对于4对极基准波旋转方向的正向和反向分别用“+”和“-”表示。

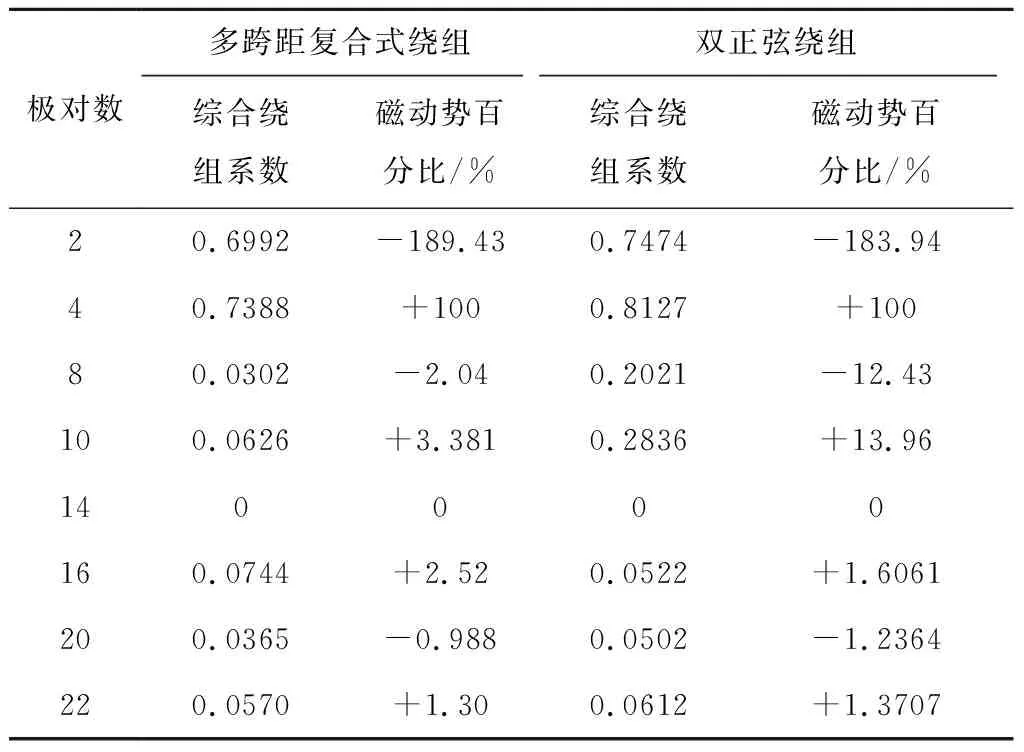
表1 两种转子绕组结构谐波分析结果对比

由表1可以看出正弦绕组的基波2/4对极的绕组系数较高，同时对高次齿谐波的抑制作用较为明显，但与基波极对数相近的8和10对极的谐波较大，谐波抑制效果不明显。复合式多跨距绕组虽然基波绕组系数相较于双正弦绕组稍低，但与基波极对数相近的8/10对极谐波得到了有效的抑制，同时对高次齿谐波的抑制作用也较为明显，最大谐波含量控制在3.4%以下，整体谐波含量较低。

4 性能对比分析

无刷双馈电机参数如表2所示，其中电压/电流大小均为有效值，根据电机参数建立的Maxwell有限元模型如图5所示，控制绕组为双层绕组跨距为8，功率绕组为单层绕组跨距为15，其中功率绕组采用角接，控制绕组采用Y接方式。

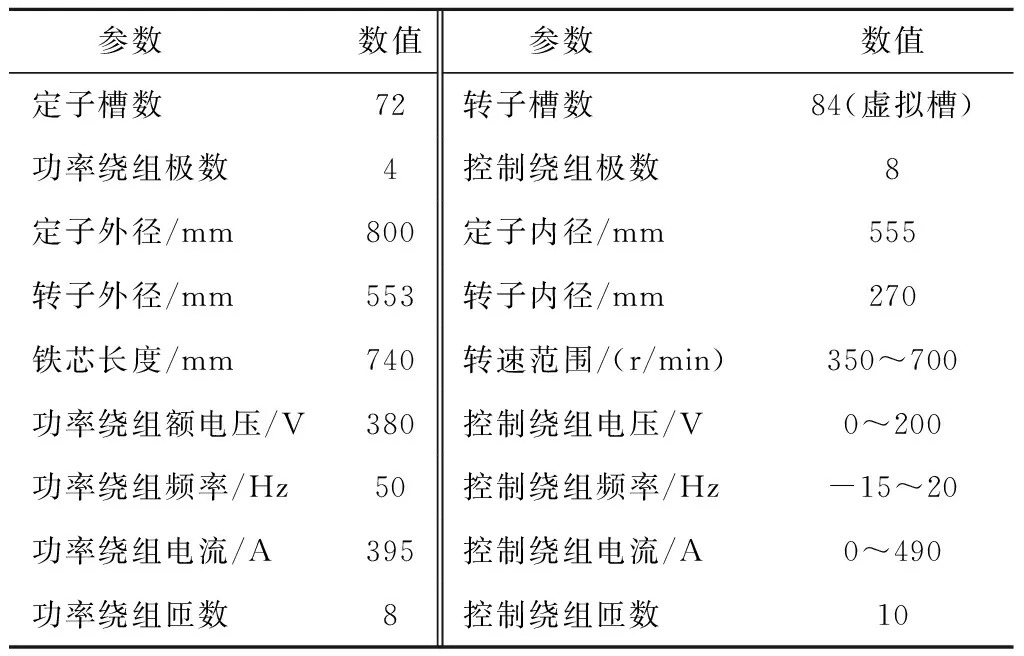
表2 无刷双馈电机主要参数

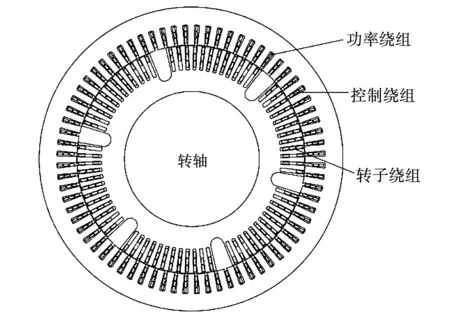
图5 无刷双馈电机有限元模型Fig.5 Finite element model of brushless doubly-fed machine

为了分析不同绕组结构的无刷双馈发电机在不同工况下的发电性能，同时为保证电机恒压恒频发电，对功率绕组端接450 kW负载下进行有限元仿真分析，同时控制绕组侧接三相电压源激励，其中控制绕组、功率绕组和转子绕组均通过外电路施加激励。

无刷双馈电机在不同工况下运行时，除控制绕组所加电压和频率不同外，不同工况下的运行特性相似，避免赘述本文仅以超同步600 r/min为例，对比分析电机在不同绕组结构下的发电性能。

4.1 发电电压谐波及输出功率分析

输出功率及谐波含量的大小是衡量电机性能的重要指标，利用有限元法对不同结构的电机输出功率及发电电压谐波进行分析，为保证结果可信，在保证定子结构，励磁电压和负载完全相同的情况下进行对比分析。此时无刷双馈电机控制绕组励磁相电压126.8 V，转速600 r/min，频率10 Hz，功率绕组侧带0.32 Ω纯电阻负载。

不同转子绕组结构下的发电电压波形和谐波分析如图6所示。电机作为发电机运行时对于功率绕组的电压输出波形要求较高，电压总畸变率是检验发电电压波形好坏的重要指标，电压总畸变率为

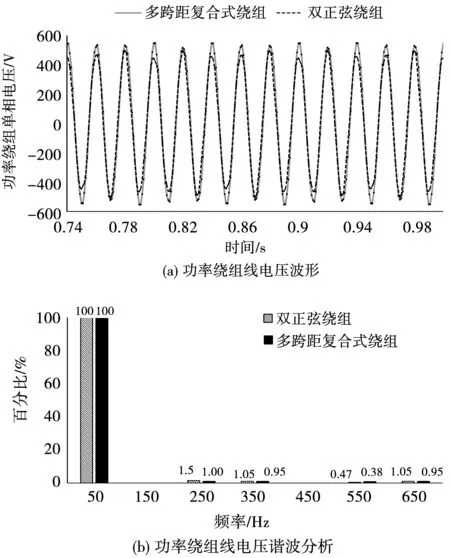
图6 不同条件下功率绕组线电压波形及谐波分析Fig.6 Line voltage waveform and harmonic analysis of power winding under different working conditions

(13)

式中:Un为第n次谐波电压有效值；U1为基波电压有效值。

转子结构分别采用基于混合式转子的复合式多跨距绕组结构的电机和普通绕线双正弦绕组电机的对比分析，线电压谐波情况如图6所示，双正弦绕组电机功率绕组侧5、7、11和13次谐波百分比分别为1.50%、1.04%、0.47%和1.05%，其电压总畸变率为2.16%。多跨距复合式绕组结构的电机对应于不同频率下的谐波百分比分别为1.00%、0.95%、0.38%和0.95%，其电压总畸变率为1.72%。由图6可知，多跨距复合式绕组电机发电电压的谐波含量小，正弦性较好；双正弦绕组电机发电电压谐波含量较高，同等励磁电压条件下，其功率绕组发出频率为50Hz的线电压有效值仅317 V。

不同转子结构下的电机功率绕组侧输出的三相瞬时功率如图7所示，由图7中不同绕组结构下的瞬时有功功率，可以计算出多跨距复合式绕组三相瞬时功率平均值为448.2 kW，双正弦绕组瞬时功率平均值为308.4 kW，同等励磁条件下基于混合式的多跨距绕组结构的电机相较于普通双正弦结构的电机输出功率约增加31.2%。可知在控制绕组给定相同励磁电压情况下，新绕组结构电机比普通双正弦绕组电机输出功率更高。

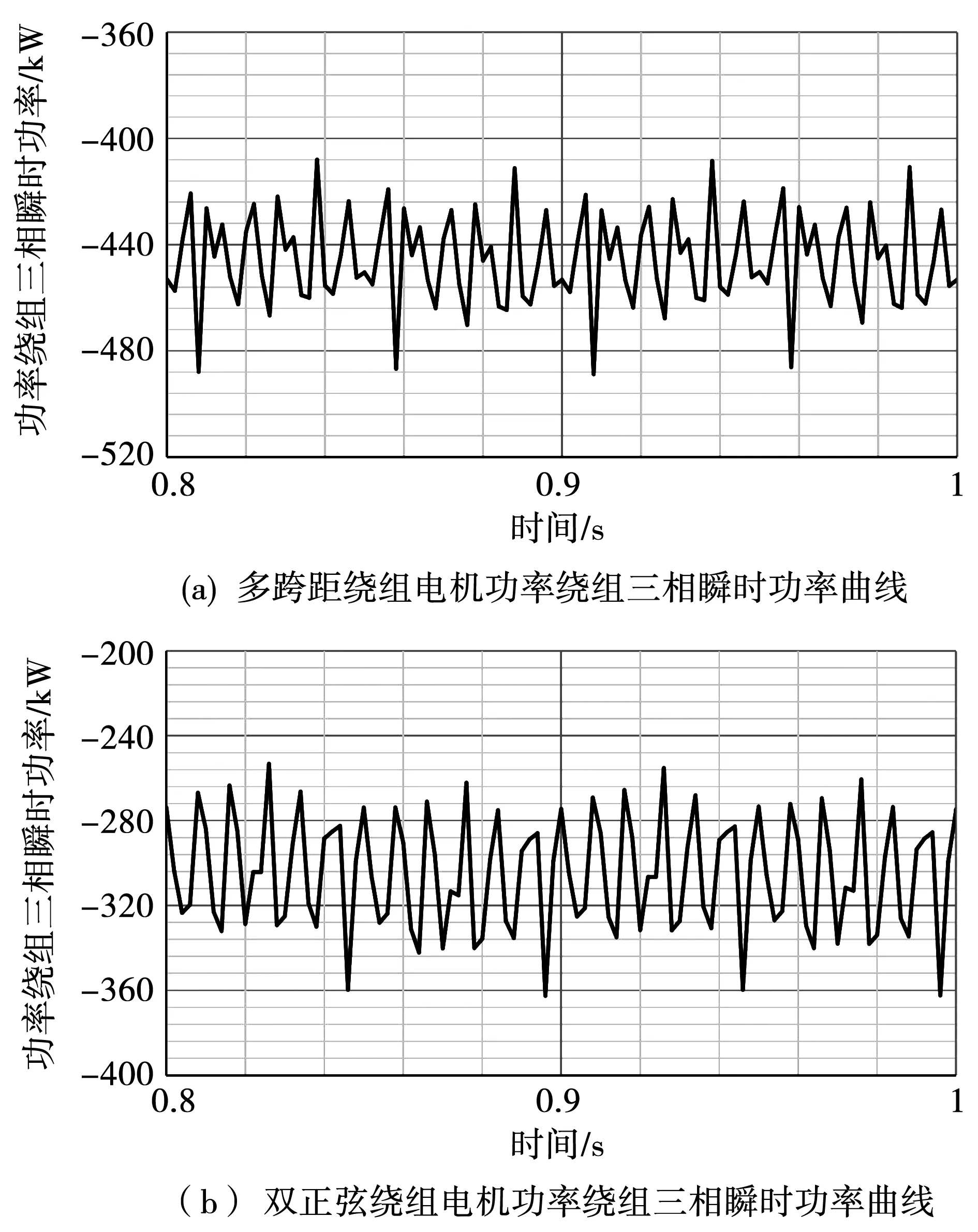
图7 不同转子绕组结构的电机输出功率对比Fig.7 Comparison of output power of motor with different rotor windings

4.2 磁场分布及气隙谐波对比分析

为研究不同转子绕组结构对电机性能的影响，在定子侧结构完全相同，控制绕组通相等励磁电压的情况下，采用场路耦合有限元分析方法，分别对转子采用基于混合式转子结构的多跨距绕组电机和普通绕线双正弦绕组结构的电机进行对比分析。

普通绕线转子结构的无刷双馈电机由于其转子绕组能够同时感应出两种不同极对数的磁动势，使得无刷双馈电机内部的磁场关系非常复杂，相较于普通异步电机，无刷双馈电机的磁场分布不具有明显的固定极对数，磁力线无固定形状。提出的磁阻绕线混合式转子结构，由于特殊的设计，磁力线分布沿着外凸极规定的方向，其内部磁力线分布较为规则，新型转子结构对电机磁力线分布具有引导作用。

不同转子绕组结构的无刷双馈电机气隙磁密曲线如图8(a)和8(b)所示，由图8和图9可知无刷双馈电机相较于普通异步电机，其气隙中谐波较为丰富，这是由于无刷双馈电机内部同时存在着多种频率的激励源以及转子绕组中同时存在着不同极对数的磁动势，导致无刷双馈电机气隙谐波较大，这也是磁场调制电机的特点。

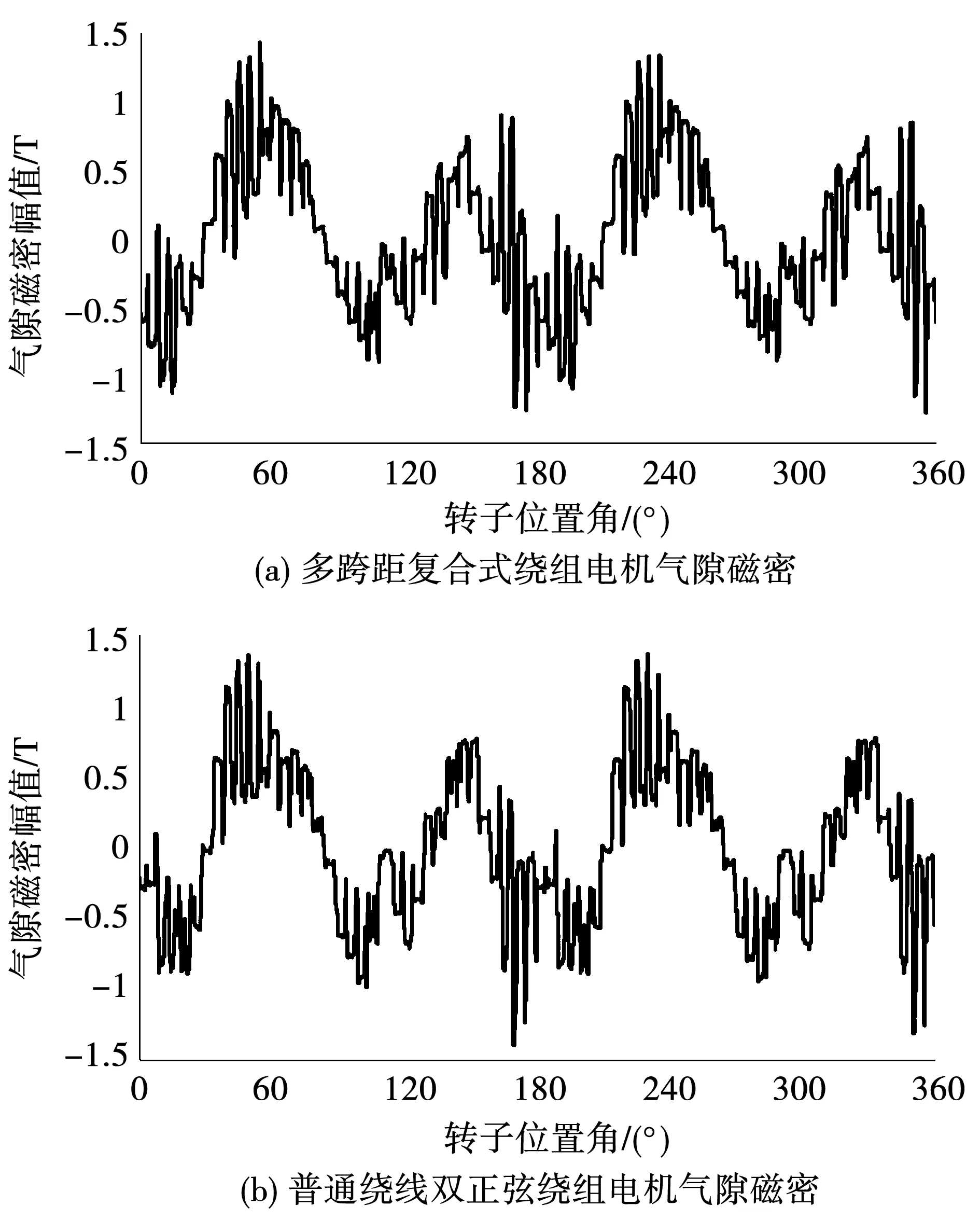
图8 不同绕组结构下电机气隙磁密分析Fig.8 Magnetic density analysis of air gap of motor with different winding structures

由图9电机气隙磁密快速傅里叶结果可以看出，给出的多跨距复合式绕组对于与主要基波极对数2/4对极相近的8/10对极谐波削弱明显，采用普通双正弦绕组设计的转子结构，气隙中8/10对极谐波较大分别为0.06 T和0.25 T，其谐波磁动势占4对极磁动势的比值为10.2%和42.1%。混合式多跨距转子结构中8/10对极谐波分别为0.05 T和0.06 T，其谐波磁动势占4对极磁动势的比值为8.4%和11.5%，可见新绕组结构对于与主要基波极对数相近的谐波削弱效果明显，这一点与前节理论分析一致，理论计算和仿真结果与文献[4]基于混合式转子设计的无刷双馈电机以及文献[16]基于多层转子绕组设计的无刷双馈电机的实验结果一致，验证了结果的正确性以及新型转子结构的电机性能在输出电压、输出功率和效率方面较为优越。

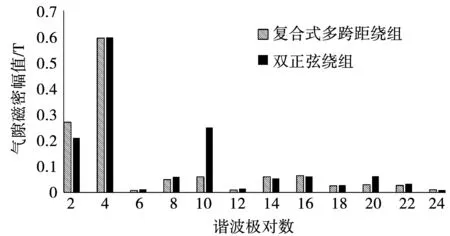
图9 不同转子绕组结构下气隙磁密谐波分析Fig.9 Harmonic analysis of air gap flux density under different rotor winding structures

同时给出的新型的磁阻绕线混合式转子结构，由于特殊的结构设计，基波主要极对数2对极相较于普通绕线转子电机有明显的增强，由图9可以看出双正弦绕组电机2对极气隙磁密幅值占4对极气隙磁密幅值的33.5%，设计的新型绕组结构电机这一比例为45.5%，可以看出提出的新型转子绕组结构相对于普通双正弦转子绕组结构能较好地增强无刷双馈电机的转子调制能力。

5 结 论

针对无刷双馈电机谐波含量大，效率低的问题，本文提出了一种基于混合式转子结构的多跨距复合式转子绕组设计方案，该结构能有效的解决无刷双馈电机导体利用率低，谐波含量大问题。

本文对多跨距复合式转子绕组结构的原理、设计步骤和规律进行了说明，并结合具体的示例进行了相关分析。同时与双正弦转子绕组进行了对比分析，结果表明该绕组结构的无刷双馈电机能有效的削弱与主要基波极对数相近的谐波含量，增强无刷双馈电机转子调制能力。

通过场路耦合有限元计算对比分析了在同等励磁电压条件下电机的谐波含量以及功率特性，结果证实了该绕组结构的电机具有输出功率大，谐波含量低，效率高的特点。