三相交流电动机不对称供电工况下磁动势的变化规律

董锋斌， 皇金锋

(陕西理工大学 电气工程学院， 陕西 汉中 723000)

电机是以磁场作为平台进行机电能量转换或传输的设备，对电机中磁场的理解影响着对电机机理的理解。磁动势是磁场中很重要的一个概念，电机的电磁转矩是定子、转子磁动势相互作用的结果，磁动势是产生转矩的直接原因[1]。交流电机电枢绕组的磁动势既与时间有关[2]，又与空间有关。在文献[3-5]中描述m相对称绕组流入m相对称电流，会在空间产生一个幅值为常数、转速恒定的圆形旋转磁动势。如果绕组不对称或电流不对称，会在空间产生一个幅值变化、转速不定的椭圆形旋转磁动势。但如何证明其幅值按照椭圆规律变化,并未给出。文献[6-7]虽然讨论了电压不对称的工况下电机旋转磁动势的特点，但主要针对缺相而展开的。文献[8]利用三相不对称系统的对称分量法将三相不对称电流分解为正序，负序和零序三组对称矢量，讨论了基波合成磁势的特点，但未分析各个区间转速变化规律。为了更清楚地分析三相交流电动机对称绕组不对称供电工况下磁动势特点，本文针对不对称供电工况下磁动势的空间运动轨迹、磁动势角速度的变化特点和磁动势角加速度的变化趋势等进行讨论，研究不同区间磁动势的变化规律，期望能给交流电机学习或研究人员提供一些思路。

1 三相交流电动机对称绕组不对称供电工况

三相交流电动机包括异步电动机和同步电动机，其定子绕组在制造工艺上一般能保证三相绕组对称，即匝数、分布系数、短距系数相同，在空间相差120°电角度。在低压配电网中，输电线路一般采用三相四线制，实际运行时三相系统各相负载很难平衡时，因内阻抗的不同，供给三相交流电机的电压实际上是不对称的，也就是说产生严格意义上的圆形旋转磁动势的条件很难满足。如图1所示，三相对称的复杂绕组可以用等效的整距绕组来代替，三相空间分布绕组的坐标用同一个坐标，原点选在A相绕组的中心轴线上。

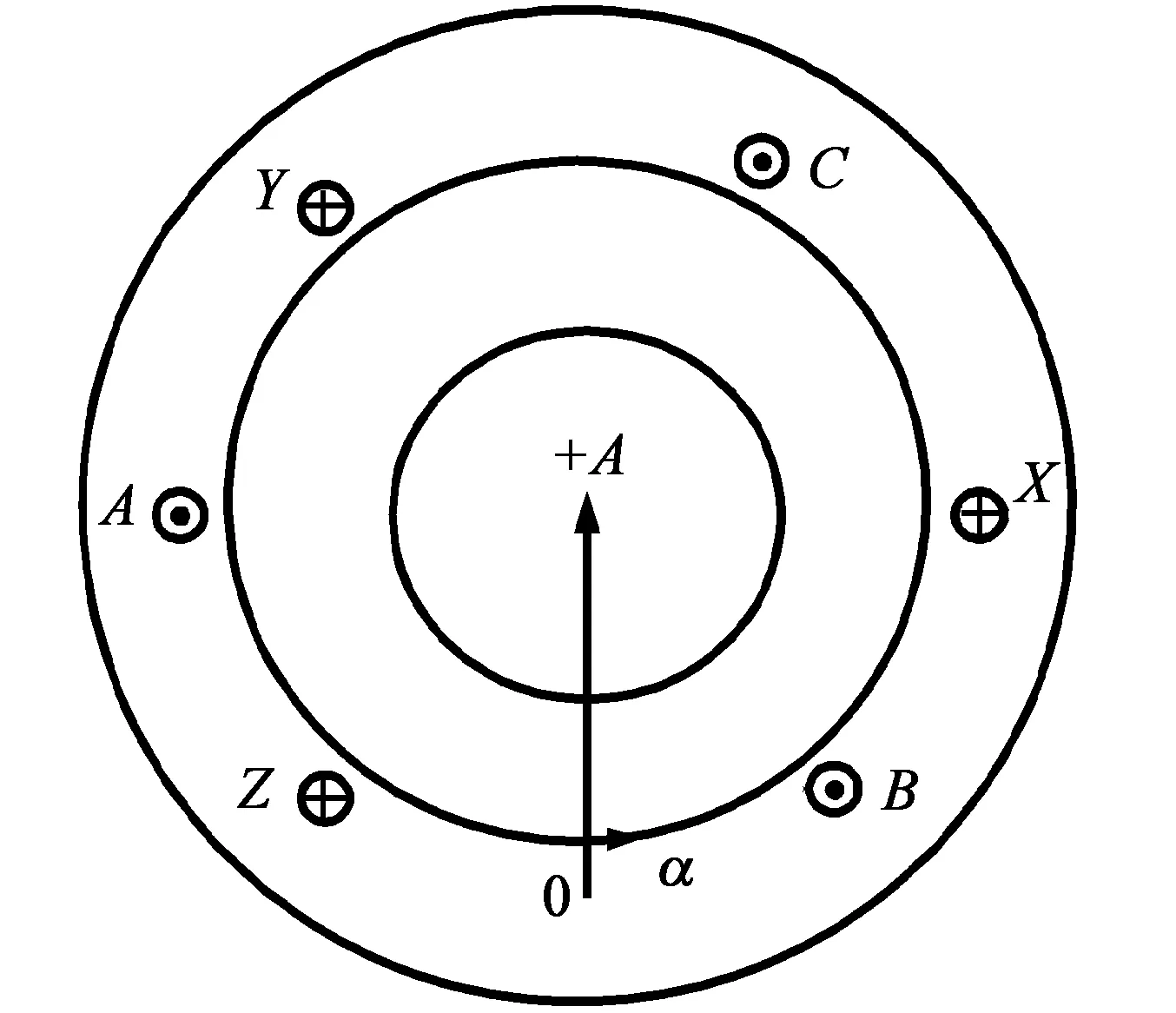
图1 等效的三相绕组

三相绕组对称，但供电电源不对称，三相绕组流过的电流依次为

其中I1、I2、I3分别为电流有效值。

三相电流在电机气隙圆周方向上产生的基波磁动势依次为

(1)

FφBcos(ωt-120°)cos(α-120°),

(2)

(3)

其中N为每相绕组串联的匝数，kdp1为绕组系数，p为电机极对数，ωt为时间电角度，α为空间电角度，FφA、FφB、FφC分别为三相基波磁动势的幅值。

2 三相交流电机对称绕组电流磁动势分析

2.1 三相交流电机基波磁动势合成

将三个单相的脉振磁动势利用三角积化和差公式、和角公式、差角公式分别分解为

(4)

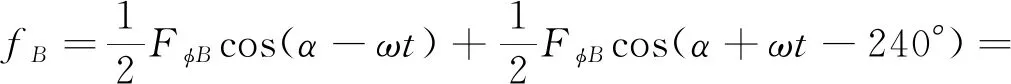
(5)

(6)

则三相合成基波磁动势为

f=(FφA+FφB+FφC)cos(α-ωt)+

F1cos(α-ωt)+F2cos(α+ωt)+F3sin(α+ωt)=f1+f2+f3,

(7)

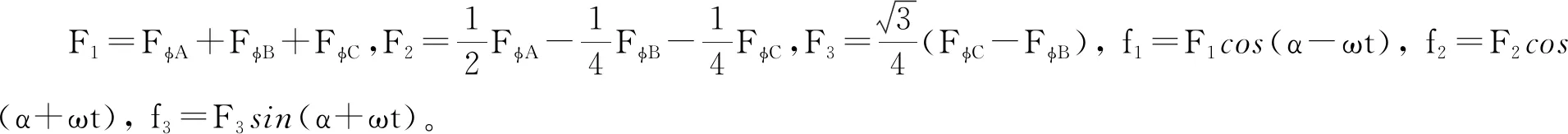
由式(7)知，合成基波磁动势由三个分量组成，f1为逆时针旋转的磁动势，f2为顺时针旋转的磁动势，f3为顺时针旋转的磁动势。

当三相电源为对称电源时，有I1=I2=I3则f=f1=F1cos(α-ωt)=1.5FφAcos(α-ωt)合成基波磁动势为逆时针旋转圆形的磁动势,此时F2=F3=0。

当三相电源为不对称电源时，F2≠0,F3≠0，合成基波磁动势为圆形磁动势还是椭圆磁动势？对此情形将进行下面的推演。

2.2 三相电源不对称分析

实际工况中分两种情况，第一种情况是有两相电流近似相等或相等，第二种情况是有三相电流均不相等。

2.2.1 两相电流近似相等或相等情形

针对第一种情况，为讨论问题方便，不妨以I1≠I2、I2=I3为例来分析合成基波磁动势的特点。

当I1≠I2、I2=I3时，F2≠0,F3=0，此时有

f++f-=F+cos(α-ωt)+F-cos(α+ωt)，

(8)

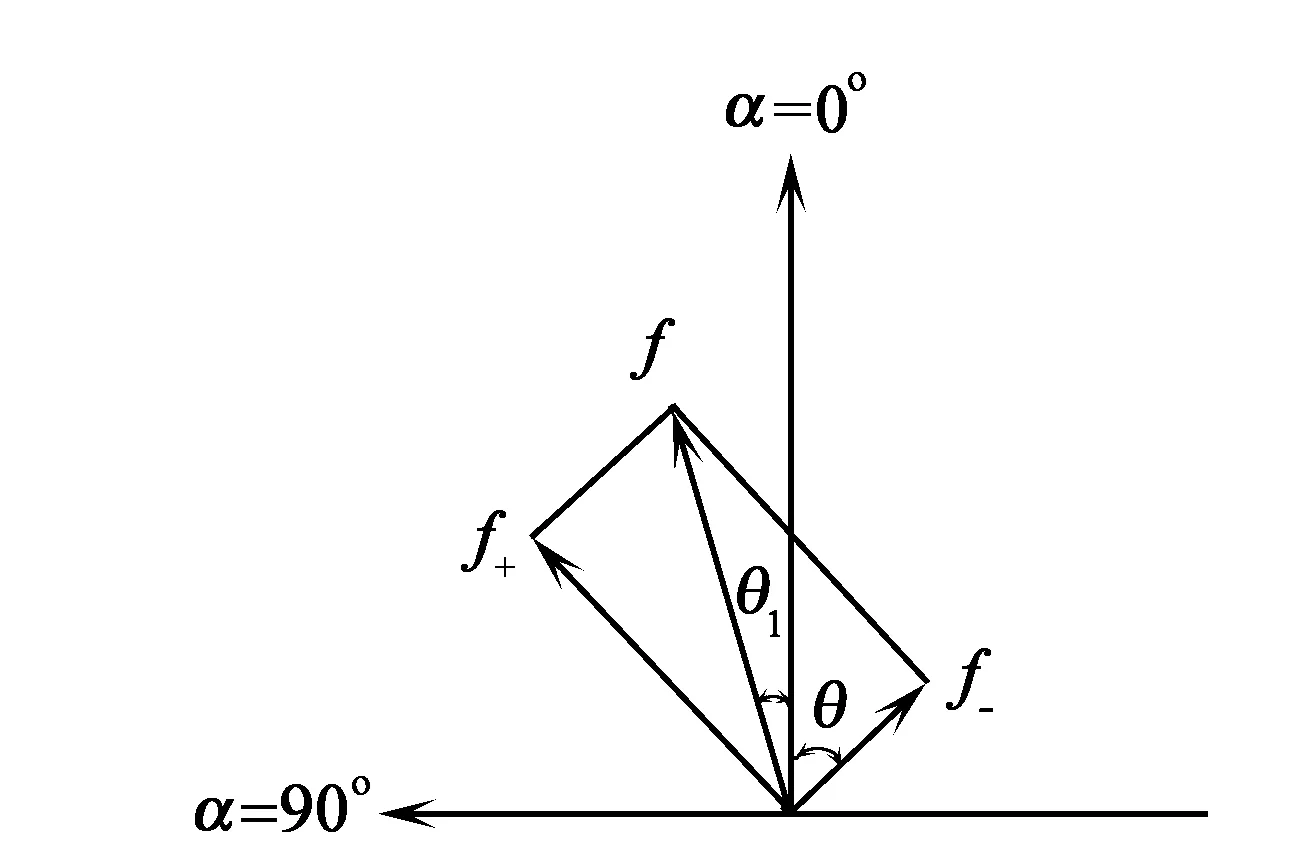
图2 磁动势向量图

(9)

其中k为三角形外接圆的直径。

f在α=0°轴线上的分量为Fcosθ1，在α=90°轴线上的分量为Fsinθ1。

由式(9)知，F+=ksin(θ+θ1),F-=ksin(θ-θ1)，F=ksin2θ。则

(10)

由式(10)知，f的运动轨迹为椭圆，其长轴为F++F-，短轴为F+-F-。用同样的方法也可证明在α∈(90°,180°)、α∈(180°,270°)、α∈(270°,360°)时f的运动轨迹均为椭圆。

f的运动速度，在α∈(0°,90°)，有θ1<θ，所以ω1<ω。一般设磁动势逆时针旋转为正，则有ω>ω1>0。

下面讨论速度的变化，由式(9)得

F+sin(θ-θ1)=F-sin(θ+θ1),

(11)

求导得

F+cos(θ-θ1)(ω-ω1)=F-cos(θ+θ1)(ω+ω1)。

(12)

在图2中根据余弦定理有

(13)

(14)

将式(13)和(14)代入式(12)中可得

(15)

从式(15)可以看出，当F+、F-、ω为定值时，磁动势的旋转速度与合成磁动势幅值的平方成反比。在α=90°时最大，在α=0°时最小。磁动势的旋转速度的最大值、最小值分别为

(16)

(17)

由式(15)知，当F+2=F2-F-2时，ω1=ω。此时对应的角度为

(18)

对式(12)求导得

(19)

因为ω是定值，则其导数为0，化简式(19)得到

(20)

由于F+>F-，θ>θ1，在θ∈(0°,90°)有cos(θ-θ1)>cos(θ+θ1)，sin(θ-θ1)>0，故dω1/dt>0。说明在此区间，ω1是变化的，而且ω1是增加的。

用同样的方法可以推导出在α∈(90°,180°)运动区间，当ω1=ω对应的角度为

(21)

在α∈(180°,270°)运动区间，当ω1=ω对应的角度为

(22)

在α∈(270°,360°)运动区间，当ω1=ω对应的角度为

(23)

在一个周期内，磁动势旋转速度的平均值和ω相等。综上所述可得到不同区间磁动势的变化规律如表1的结论。

表1 不同区间磁动势的变化规律

2.2.2 三相电流均不等情形

对于第二种三相电流均不相等的情况，f2和f3是幅值固定且有相同速度的顺时针旋转磁动势，其合成磁动势为幅值固定、速度恒定的顺时针旋转磁动势，和第一种情况下的f-性质类似。这种工况下的基波合成磁动势分析过程和第一种情况下雷同，这里不再讨论。

3 结论

当三相电源为不对称电源时，其合成基波磁动势则为椭圆磁动势。基波磁动势的旋转速度在变化，在不同的象限区间内速度或增或减，但其转速在一个周期的平均值和圆形旋转磁动势的速度有ω相等。虽然以I1≠I2、I2=I3为例来分析合成基波磁动势的特点，但对于I1≠I2≠I3的工况其上述结论仍然适用。三相电机在不对称电压下运行，其合成基波磁动势则为椭圆磁动势会导致电机过载能力和效率降低，温升提高，所以应尽量使电机在对称三相电压下运行。