双螺杆空压机壳体结构振动特性研究

何亚银， 高卫丽， 梁智鸿

(1.陕西理工大学 机械工程学院， 陕西 汉中 723000；2.陕西省工业自动化重点实验室， 陕西 汉中 723000)

双螺杆空压机由一对阴阳转子、壳体和轴承等零部件组成，工作循环可分为进气、压缩和排气3个过程，随着转子旋转，每对相互啮合的齿相继完成相同的工作循环[1]。由于双螺杆空压机可靠性高、操作维修方便、动力平衡性好、适应性强，可广泛应用于矿山、化工、动力、冶金、建筑、机械、制冷等工业领域[1-2]。因此，双螺杆空压机已经成为制造业的主要动力能源。

空压机作为提供动力的核心装置，其壳体是其重要的承载部件，在使用过程中受到了各方面的振动激励作用，一旦发生共振，将产生极大的动载荷，破坏空压机系统工作时的稳定性和降低壳体使用寿命，严重时导致断裂失效。因此，为了能够保证空压机壳体强度和刚度，研究壳体的振动特性很有必要。

国内外学者对双螺杆空压机在力学性能、仿真分析和振动分析等方面开展了一系列的研究，取得了一些研究成果。如张天翼等[3]对螺杆压缩机壳体结构进行设计和优化；尹辉俊等[4]利用有限元分析和试验测试的分析方式对空压机车架结构的振动特性进行了研究；吴慧媛等[5]对双螺杆压缩机进行了流场动力学特性分析；赵佳磊等[6]对螺杆转子进行建模及模态分析；丁一[7]对滚动转子压缩机空调系统进行了振动与结构的有限元分析；杨胜梅等[8]对螺杆压缩机壳体进行了设计优化；赵宁等[9]对螺杆转子进行动力学性能有限元分析；冯博琳[10]对螺杆转子进行了基于模态分析的结构仿真；Ferraris G等[11]利用转子动力学、有限元方法和影响系数法以减少压缩机转子与定子部分的振动；Kim S G等[12]使用有限元分析方法，降低了压缩机的振动和噪声。

上述文献多数是对空压机的动力学、静力学和结构设计研究，而在双螺杆空压机工作过程中，由于转子啮合转动、驱动电机工作及空压机支撑架引起壳体振动产生裂纹，甚至遭受破坏，将会导致整个空压机工作进程停止，产气质量下降。因此，需要对双螺杆空压机壳体的振动动态特性进行分析，从而为双螺杆空压机的合理工况参数的设定提供依据。

本文采用有限元分析方法，对双螺杆空压机壳体的结构振动特性进行研究，计算壳体模态，得到各阶固有频率，利用模态分析结果，对壳体进行振动谐响应分析，确定动态性能影响最大的模态频率，并对结果进行分析。

1 模态分析及谐响应理论基础

对于一个多自由度系统，其整体动力平衡方程为[13]

(1)

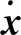
模态分析是分析结构的固有动力学特性，与结构所受载荷形式无关，其目的是得到结构固有频率和相应的模态振型，模态分析是在施加零位移约束的前提下，求解结构的固有频率及相应的模态振型[14]，方程变为

(2)

谐响应分析是一种线性分析技术，分析结构在不同频率荷载下的振动特性，它要求结构所受载荷全部是简谐荷载，并且在分析过程中需要设定荷载的频率范围，通过对结构件的谐响应分析，可以得到结构的稳态动力特性，从而使设计人员能够验证其是否产生共振或受其它外界影响产生振动，进而改进设计。谐响应分析是在发生谐振动时，即x=Xsin(ωt)时，对结构输入一个随时间按正弦规律变化的动载荷，求解结构的振动响应[15]，即将x=Xsin(ωt)代入式(2)，可得

(3)

式中ωi为固有圆周频率，φi为振型。

2 建立空压机壳体有限元模型

2.1 空压机壳体的几何模型建立

本文的研究对象为YSJ-03型双螺杆空压机壳体，其中空压机电机转速为2950 r/min，功率为22 kW，排气压力为0.8 MPa，压缩机排量为3 m3/min。由于双螺杆空压机壳体结构复杂，为方便网格划分、节约计算资源、缩短计算时间，在符合实际要求和不影响计算准确性的条件下，对壳体的三维实体建模过程做了适当的简化处理，设计参数如表1所示，利用UG建立壳体的三维实体模型如图1所示。

表1 双螺杆空压机壳体设计参数

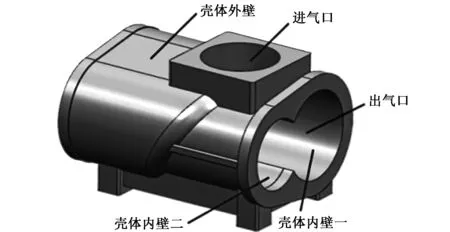
图1 壳体三维实体简化模型

2.2 网格划分及边界条件

本研究采用的双螺杆空压机壳体的材料为灰铸铁HT250，其主要相关材料属性如表2所示。根据双螺杆空压机壳体结构及性能要求，选取单元尺寸为5 mm对模型进行离散。最终的网格划分结果共得到了131 050个节点，75 601个网格单元，整体网格质量为0.723 29，壳体网格划分模型如图2所示。

图2 壳体网格划分模型图

表2 HT250主要相关属性参数

对壳体施加约束，由于模态分析是针对系统的固有特性，与系统所受载荷无关，只需要对壳体底部施加固定约束，而且由模态分析相关理论可知，在结构振动过程中起主要作用的是低阶模态，而高阶模态影响较小，且下降速度很快，所以将模态数目设置为6阶；谐响应振动分析，通常作用于壳体上的载荷一个是转子啮合转动对壳体产生的压力，另一个是进气端口和出气端口对壳体的动载荷，考虑双螺杆空压机的实际情况，对出气口施加压力载荷0.8 MPa，并结合模态分析结果对双螺杆空压机壳体谐响应分析施加激振频率范围。

3 空压机壳体仿真分析结果

3.1 模态分析

根据本文模型特点，采用分块兰索斯法(Block Lanczos)作为壳体的模态提取方法。模态振型如图3所示，最终模态分析得到壳体的前6阶固有频率如表3所示。

图3 壳体前6阶模态振型图

表3 壳体前6阶模态振型特点

通过对前6阶模态分析结果可以看出，1阶振型下的壳体在出气口处产生绕Z轴摆动的振动；2阶振型下的壳体不仅出现出气口处产生绕Z轴摆动的振动，而且壳体局部也开始弯曲变形；3阶振型下的壳体上侧进气口变形严重，壳体两侧向内凹陷，电机端开始变形；4阶振型下的壳体的出气端开始在XY平面发生扭转；5阶振型下的壳体出气口严重扭转弯曲，进气口变形，壳体局部发生弯曲；6阶振型下的壳体在XZ平面发生凹陷，出气口扭转。综上所述，壳体主要是发生了一些弯曲、摆动和扭转振动变形，且壳体低阶模态分析变形较大的区域主要集中在进气口和出气口，这两个地方变形较大，易产生大的应力，容易造成疲劳裂纹和断裂的现象。因此，双螺杆空压机壳体在设计时应加强出气口和进气口这两部分的刚度及强度。

3.2 谐响应分析

鉴于双螺杆空压机的工作特点，由电机带动转子啮合转动，从而引起壳体振动，产生噪声影响空压机的工作效率；此外由于空压机机头放置在车架上，电机转动引起车架振动，从而对空压机机头产生影响，因此对壳体在工作过程中产生振动现象进行谐响应分析研究。经过对双螺杆空压机的运行环境等综合因素考虑并对几种方法优缺点比较，本文采用模态叠加法对空压机壳体进行谐响应计算，对出气口施加压力0.8 MPa,由模态分析确定所施加的激振频率范围设置为700～2400 Hz，求解间隔为50 Hz。进行谐响应分析后查看结果得到壳体X、Y、Z三个方向的位移、应变、应力与频率之间的具体关系，如图4所示。

图4 壳体的振动位移、应变、应力-频率曲线图

从图4中可以看出：(1)当频率达到1074 Hz时，壳体在Y方向和Z方向上出现最大的位移峰值；当频率达到1448 Hz时，Y方向和Z方向出现第二次位移峰值，但其峰值明显小于1074 Hz时的位移值；当频率达到2366 Hz时，在Y方向和Z方向又出现较大的位移值。(2)当频率达到1074 Hz时，壳体在X、Y、Z方向上出现最大的应变，且Y方向的应变大于X、Z方向的应变；当频率达到1448 Hz时，X、Y、Z方向出现第二次应变峰值，但其峰值明显小于1074 Hz时的应变值；当频率达到2366 Hz时，在X、Y、Z方向出现较大的应变值。(3)当频率达到1074 Hz时，壳体在X、Y、Z方向上出现最大的应力，Y方向的应力大于X、Z方向的应力；随着频率达到1448 Hz，X、Y、Z方向出现第二次应力峰值，但其峰值明显小于1074 Hz时的应力值；当频率达到2366 Hz时，在X、Y、Z方向出现较大的应力值。

从壳体的振动位移、应变、应力-频率曲线图可以看出，随着激振频率的不断增大，振动位移、应力和应变在1074、1448、2366 Hz这3个频率下出现了峰值，且频率对应与模态分析的第2阶、第3阶及第6阶固有频率接近。图5为响应频率为1074 Hz时，即响应最为强烈时的应力、应变振动云图。

图5 壳体在频率1074 Hz下的应力、应变振动云图

壳体在工作过程中不仅受到转子啮合振动，还受到了空压机车架的振动，很容易在应力变形较大的地方发生共振产生破坏。观察图5可以看出壳体最大变形结果发生在壳体出气口及进气口，因此可以推断出在壳体的第2阶、第3阶及第6阶固有频率下，极有可能出现共振问题，在设计时应避免这3个频率。

4 结论

(1)通过对壳体的模态分析，可知变形较大的区域主要集中在进气口和出气口，这两个地方易产生大的应力，造成疲劳裂纹和断裂的现象，且壳体铸造件一般为灰铁件，属于脆性材料。因此，双螺杆空压机壳体在结构设计时应加强出气口和进气口这两部分的刚度及强度，提升产品质量，此外还可以选取强度和刚度较高的材质进行壳体的加工制造。

(2)在频率1074、1448、2366 Hz这3个频率下应力变形比较大，且壳体的动态性能影响较大，极有可能出现共振问题。由于壳体受到电机和螺杆转子的共同激励，因此为了保证正常工作应尽可能避免与此频率相同。此结果可为后续优化壳体结构、解决壳体振动问题提供参考依据。