双螺杆真空泵螺杆转子热力耦合分析

王智博， 李志峰， 晁 瑞， 朱博文

(陕西理工大学 机械工程学院， 陕西 汉中 723000)

螺杆真空泵由于其优越的性能，在微电子、半导体以及制药等多个领域备受青睐。螺杆真空泵利用一对相互啮合的螺杆在泵腔内进行同步高速反转而产生吸气和排气作用，螺杆转子在运转时转子之间以及转子与泵腔之间留有一定间隙，处于非接触状态。然而，螺杆在运转过程时会对气体做功，从而产生很多热量，导致转子温度快速升高，从而使其产生热力变形，导致两转子卡死，泵不能正常工作。因此研究螺杆转子的热力变形，合理设置阴阳转子的装配间隙，成为研究螺杆转子性能的关键。

刘春姐等[1]考虑螺杆转子传热和对流换热，利用有限元分析方法，对干式螺杆真空泵转子温度场进行研究，得出螺杆转子温度分布规律；孙瑾亭等[2]对螺杆真空泵主动转子的温度场和热变形进行分析，得到转子的温度分布规律；徐建宁等[3]利用有限元分析建立同步式双螺杆泵螺杆的温度场及热变形分析模型,对螺杆转子在工作过程中的的温度场和热变形进行模拟分析；张庆东等[4]以3种不同冷却结构转子为研究对象，建立温度场有限元模型，计算了3种冷却结构转子的温度场和热变形，分析了不同冷却结构对转子热形变量的影响；魏静等[5]以某新型双螺杆捏合机螺杆转子为研究对象,实现热—流—固耦合的数值模拟，得出热变形是转子实际工作中变形的主要原因；张强等[6]以螺杆泵定子衬套为研究对象，建立定子衬套摩擦生热的双向热力耦合模型,得出配合关系和摩擦系数超过某一数值时的温度分布规律;唐远富等[7]计算出转子的对流换热系数并施加边界条件进行有限元热结构间接耦合分析，得出转子启动过程的应力分布规律和应力集中的部位;叶振环等[8]考虑圆柱滚子轴承运转过程中存在热力相互作用的影响，建立热力耦合分析模型，对比分析了考虑到热力耦合与不考虑热力耦合作用下温度分布；刘玲[9]通过研究矿用带式输送机鼓式制动器，建立有限元分析模型并进行热力耦合分析，得出网格划分尺寸大小对制动温度场影响比较大,材料物料参数对制动温度场也有一定程度上的影响；张深远等[10]以等螺距螺杆转子为研究对象，对3种不同冷却结构的螺杆转子进行热力耦合分析，得出螺杆转子的温度场分布规律和热力形变分布规律。

诸多学者对螺杆真空泵螺杆转子的稳态温度场分布和热变形分布规律进行研究，为螺杆真空泵螺杆转子热学分析做出很多贡献。然而以往研究仅仅局限于对螺杆真空泵螺杆转子进行温度场和热形变分析，未考虑螺杆转子热力耦合作用，没有贴近螺杆真空泵真实工作情况，不能对螺杆转子变形量做出合理分析，从而不能给出螺杆转子合理装配的设计间隙。

针对上述问题，考虑到螺杆转子热力相互作用，本研究利用ANSYS Workbench分析软件，先对螺杆转子施加温度载荷进行温度场仿真计算，得到螺杆转子温度变化；再将温度变化加载在螺杆转子表面进行应力场的分析计算，从而获得螺杆转子热力变形云图并进行分析，为转子转配间隙的合理设计提供理论依据。

1 数学模型

1.1 热力学模型

基于传热理论和热弹性分析理论，利用有限元分析软件对螺杆真空泵螺杆转子的传热问题进行分析求解，得到螺杆转子的温度变化分布情况以及热变形和热力耦合变形结果。

稳态热力学分析一般方程：

[K]{I}={Q}，

(1)

式中{Q}表示节点热流向量，[K]表示传导矩阵，{I}表示节点温度向量。

在稳态热分析中温度不随时间变化而变化，其中对流换热系数和热流量也不随时间变化，流入系统中的热量等于流出系统的能量。在笛卡尔直角坐标系中，温度场可以用温度T关于位移和时间的函数表示：

T=f(x,y,z,t)，

(2)

式中T表示温度，单位为℃；x、y、z表示三维空间坐标，单位为m或mm；t表示时间，单位为s。

假设螺杆转子介质连续均匀、各向同性，在稳态、无内热源条件下，导热微分方程简化为

(3)

完全接触的两个物体或者一个物体的不同部分之间由于温度梯度而引起的内能交换，称之为导热[11]。螺杆转子各个轴段温差引起的内部能量交换，遵循傅里叶公式：

(4)

由于螺杆转子输送的是有一定温度的气体介质，能与螺杆转子表面进行强制对流换热。对流换热可以用牛顿冷却定律方程描述：

q=h(TB-Tf),

(5)

式中q表示螺杆转子的热流密度，单位为W/m2；h表示螺杆转子与空气的对流换热系数；TB表示螺杆转子表面的温度；Tf表示螺杆转子周围气体的温度。

1.2 力学模型

基于经典力学理论哈密尔顿法则，建立真空泵螺杆转子的运动方程：

(6)

2 有限元模型前处理

以螺杆转子为研究对象，通过Pro/E建立螺杆转子的几何模型，将几何模型导入ANSYS Workbench有限元分析软件中，计算求解得到稳态温度场，并与应力场进行间接耦合，得到螺杆转子的温度场分布云图以及热形变云图。

2.1 几何模型建立

本研究所选用的螺杆转子材料是30CrMnTi合金，含碳量为0.24%～0.32%，渗碳及淬火后具有耐磨性好、静强度高的特点，可用于制造心部强度特高的渗碳零件，如齿轮轴、齿轮、蜗杆等，其物理参数如表1所示。

表1 30CrMnTi材料参数

螺杆转子端面型线由多段不规则的曲线组成，其中包括摆线、渐开线、齿顶圆和齿根圆弧线等组成，仅靠ANSYS软件自带建模工具难以完成螺杆转子的建模，因此要借助于三维建模软件进行几何模型的建立。常用的的几何建模软件有UG、SolidWorks和Pro/E等。本文通过将某一型号阴、阳螺杆转子端面型线离散数据点分别导入Pro/E，生成各自端面型线，再建立螺旋线，扫掠生成阴、阳转子，完成螺杆转子的三维建模，并对其进行装配和干涉检查，保证工作运转正常。

2.2 网格划分及边界条件

对几何模型进行有效地网格划分是ANSYS仿真分析的前提，网格尺寸及等级的大小直接对仿真结果造成影响。将Pro/E建立螺杆转子的几何模型导入ANSYS有限元分析软件中，为高效准确地进行网格划分，需要对螺杆转子模型进行简化，省略螺杆轴上的倒角。对螺杆转子的网格划分类型是实体四面体单元，对螺杆表面进行加密划分，优点是四面体网格划分相对较为简单，网格划分时能考虑到几何体边界层上网格的设置等。如图1所示，划分后的网格节点数为629 944，网格单元数为397 403。

图1 螺杆网格单元划分

螺杆转子的结构是一个回转体，在任何机械结构中均采用简支梁的支撑约束，因此，安装轴承时要确保螺杆转子的一端固定，螺杆转子的另一端能够自由伸缩。为了保持排气端与壳体的距离恒定，减少容积气体泄漏和避免螺杆轴端面磨损，螺杆转子在排气端采用轴向定位，确保排气端有着恒定的最小轴向间隙，而进气端有较大的轴向间隙，使进气端能够自由伸缩。在螺杆转子的进气端，限制沿x、y方向位移自由度、绕x、y轴旋转自由度和沿z方向位移自由度；在螺杆转子的排气端，限制沿x、y、z方向位移自由度、绕x、y轴旋转自由度，保留沿z方向位移自由度和绕z轴旋转自由度。

由工厂测量得出，双螺杆真空泵进入稳定工作状态后，在设有冷却系统的情况下，进气端温度能够稳定在25 ℃，排气端温度稳定在85 ℃。以输送气体的温度为30 ℃，环境温度为25 ℃，对螺杆转子施加温度载荷：第一类边界条件为螺杆转子温度施加在螺杆转子的进气端与排气端，取螺杆转子进气端温度为35 ℃、排气端温度为85 ℃；第二类边界条件由经验值采用热流密度q=20 W/mm2，加载在外螺杆转子表面；第三类边界条件取对流换热系数80 W/(m2·℃)，流体温度为气体温度30 ℃，加载在螺杆转子外表面。

3 仿真结果及分析

3.1 稳态温度场的变化

在ANSYS稳态温度场仿真计算结果中，得到转子温度场分布云图以及螺杆转子温度场轴剖图，分别如图2和图3所示。

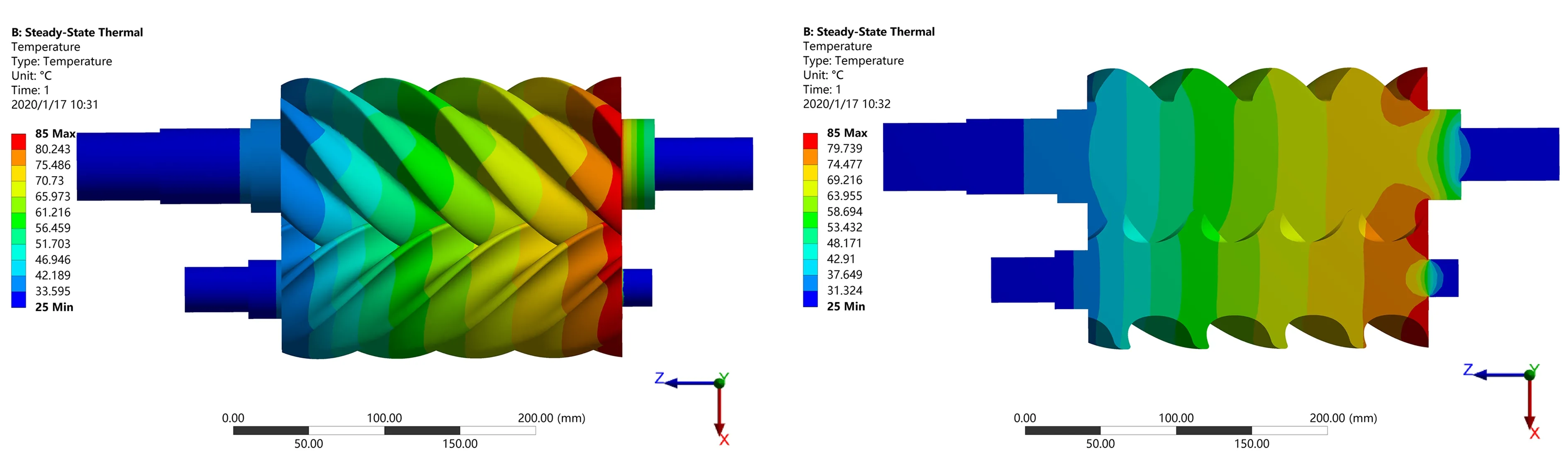
图2 螺杆转子温度场分布云图 图3 螺杆转子温度场轴剖图

由图2可发现，螺杆转子进气端温度在25 ℃左右，排气端温度在85 ℃左右，螺杆转子整体温度变化较为均匀，基本呈线性变化，阴、阳转子的温度场分布规律也近似，纵向跨度均匀。温度场变化趋势沿轴向从进气端向排气端逐渐上升，这是因为转子材料具有的良好的物理参数和自身几何结构对称的特点决定的。

由图3可知，加载温度为35 ℃的进气端附近，齿面的温度略低于轴心的温度；转子的中间部分齿面温度与轴心温度无明显差异；加载温度为80 ℃的排气端附近，轴心的温度略低于齿面的温度。处于同一轴截面上，齿面可以直接与热源接触，可以更好地从热源吸收热量，而轴心通过齿面传导热量，吸收热量相对齿面较慢、较少，但是螺杆转子所处的环境温度为35 ℃，齿面的温度散失也比较快。在螺杆转子排气端附近，齿面从热源吸收热量的优势大于散热的劣势，以致于转子的齿面温度高于轴心的温度。在螺杆转子的进气端附近，齿面从热源吸收热量的优势较排气端吸热优势较差一些，齿面散热的劣势仍然不变，导致转子齿面温度略低于轴心的温度。另外在一定程度上，材料的导热率随温度变化而变化。

3.2 温度场作用对螺杆转子的变形影响

图4所示为螺杆转子各个方向的热变形曲线图和总热变形云图，可以看出螺杆转子在x、y轴方向的变形趋势相似，且沿x、y轴方向的变形量大于沿z轴方向的变形量，各个方向最大变形量和最大总变形量位于阴转子的齿顶圆位置。由图4(a)、(b)可知，螺杆转子在x、y轴方向的阴转子变形量明显大于阳转子，x轴方向最大变形量为0.527 44 mm，y轴方向最大变形量为0.338 52 mm；螺杆转子在z轴方向上变形量较均匀，进气端变形量大于排气端变形量，最大变形量为0.200 11 mm；由图4(c)可知，螺杆转子阳转子总变形量小于阴转子总变形量，最大变形量为0.584 31 mm。

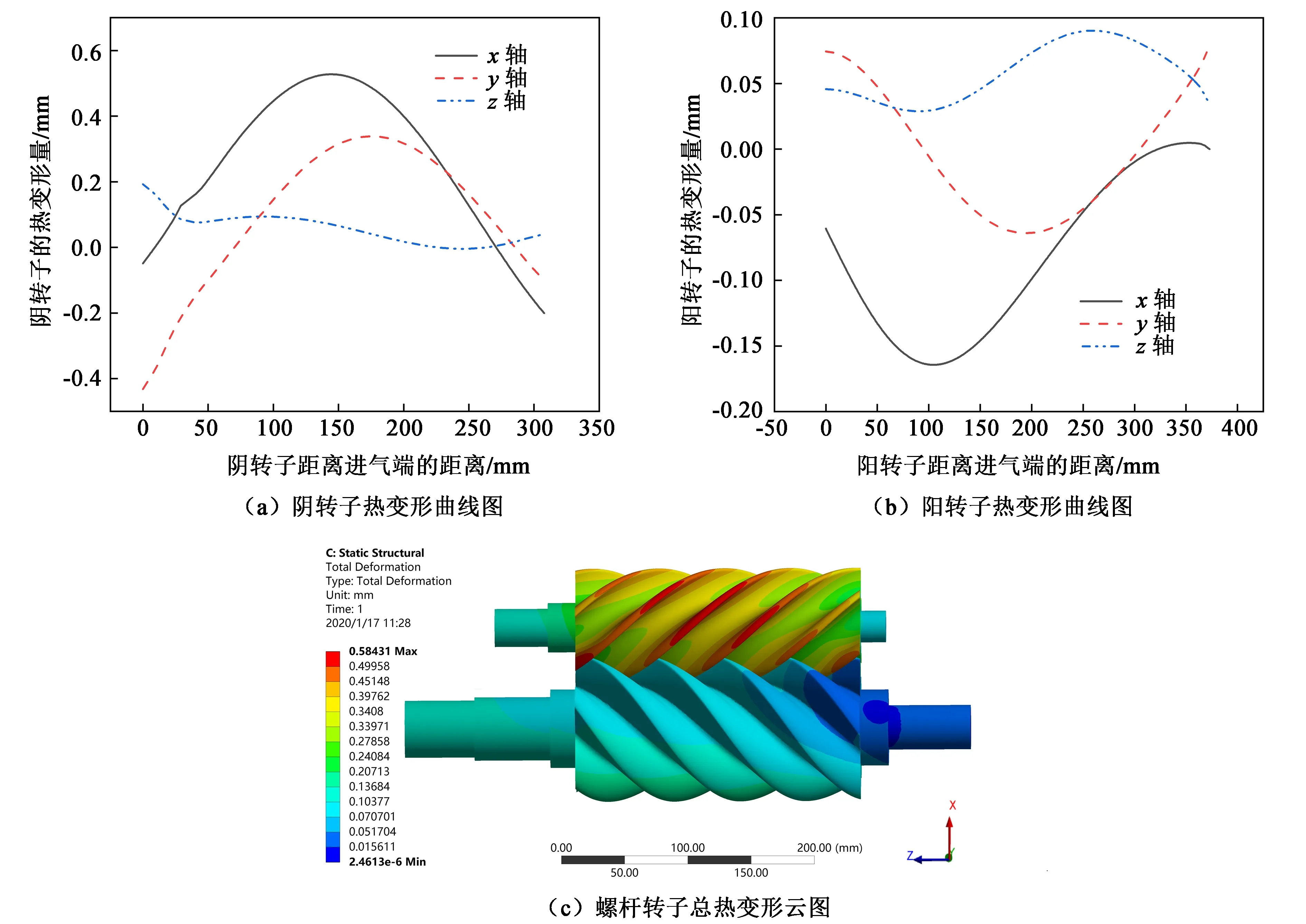
图4 螺杆转子各方向热变形云图

3.3 热力耦合作用对螺杆转子的变形影响

将温度场作为外载荷施加在螺杆的表面，再对螺杆加载工作约束条件，通过数值模拟分析螺杆转子各个方向的热力变形曲线图和总热力变形，如图5所示。

图5 螺杆转子各方向热力变形云图

结合表2数据可以看出螺杆转子在各个方向热力变形变化规律与热变形的变化规律相同，变形量略大于热变形，说明温度是影响螺杆转子变形的主要因素。由图5(a)、(b)、(c)以及表2可知，螺杆转子在x方向上最大热力变形量为0.527 59 mm，比热变形增加了0.000 15 mm；螺杆转子在y方向上最大热力变形量为0.338 67 mm，比热变形增加了0.000 15 mm；螺杆转子在z方向上最大热力变形量为0.200 13 mm，比热变形增加了0.000 02 mm；螺杆转子最大总变形量0.584 46 mm，比热变形增加了0.000 15 mm。

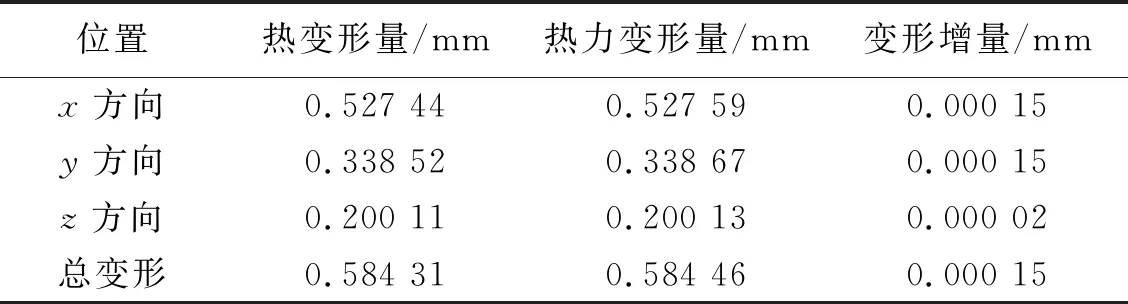
表2 热变形量及热力变形量表

由图6可知，阳转子轴心形变量曲线变化较为平缓，阴转子轴心形变量曲线变化较大，热变形量和热力变形量曲线基本重合，阴转子轴心变形量明显大于阳转子的轴线变形量，进气端的变形量高于排气端变形量，这都与热变形云图和热力变形云图相符合。

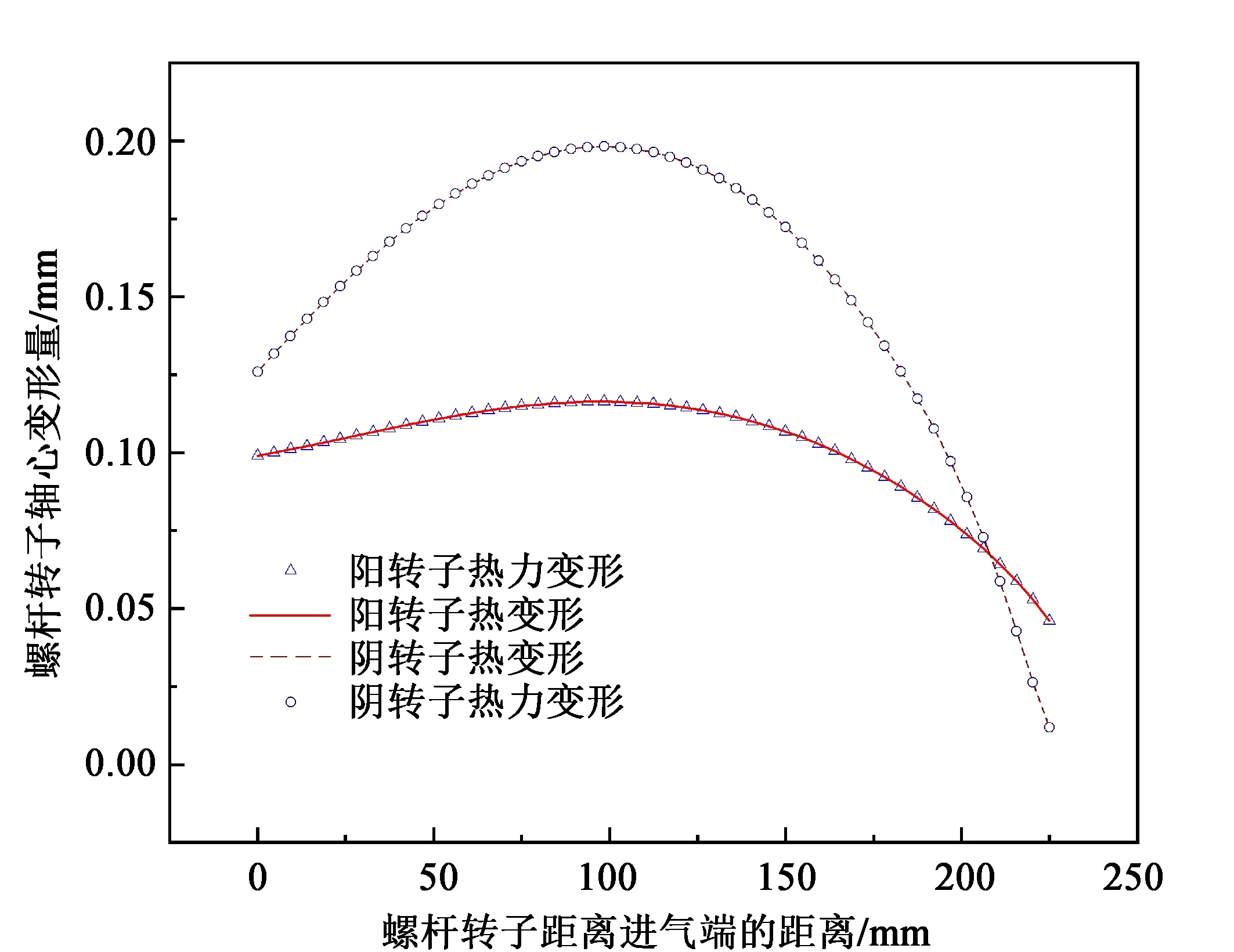
图6 螺杆转子轴心形变量曲线图

4 结语

本文利用ANSYS Workbench对双螺杆真空泵螺杆转子进行热力耦合分析，主要得到以下结论：

(1)从稳态温度场计算结果可知，温度变化从进气端向排气端逐渐增加，进气口温度比较低，排气端温度最高，且进气端齿面温度低于轴心温度，排气端齿面温度高于轴心温度。

(2)通过热变形量和热力变形量结果可得，阴转子变形量大于阳转子的变形量，对比热变形量和热力变形结果发现温度是影响螺杆转子变形的主要因素。

(3)考虑到双螺杆真空泵工作过程中存在热力相互耦合作用，建立数值模拟模型并进行分析，确定了螺杆转子最大变形量，为螺杆转子啮合装配间隙提供了理论依据。