考虑谐波磁动势的双边直线感应电机推力特性计算
刘慧娟,王 宇,张 千,吕 刚
(北京交通大学电气工程学院,北京 100044)
直线电机具有结构简单、稳定性强、运行速度快等特点,可以直接将电能转换为机械能,因此被广泛地应用在机械传输、电磁弹射、交通运输等领域[1].短初级DLIM 因其初级长度短、制造成本低等特点,在轨道交通等领域具有独特的应用优势[2].目前对直线感应电机的优化设计和电磁性能计算主要采用解析法和有限元法[3-4],从控制策略和结构优化等方面提升电机的电磁性能[5-6].
直线电机的推力特性是衡量其性能优越的重要指标,由绕组产生的磁动势是影响电磁推力的重要因素.磁动势分布随绕组结构的变化而变化,目前常见的绕组形式有分布式绕组、集中绕组、环形绕组[7],绕组外部连接方式主要有三角形连接、星形连接和开放式连接等[8].文献[9]提出了一种不同于传统双层绕组的新型双层无槽集中绕组,提高了绕组系数和推力密度.文献[10-11]依据绕组结构,对比分析了间隔绕组、全齿绕组,集中绕组、分布绕组对直线电机推力的影响.
电机实际运行时,初级绕组中通入三相对称电流,会产生周期性阶梯形磁动势波[12],可分别采用矢量法和积分法求取交直流电机的磁动势值[13].在实际计算过程中,为了简化计算过程,通常忽略了磁动势谐波作用,只考虑基波磁动势对电机性能的影响.在未考虑谐波磁动势时,文献[14]针对三相交流电机不对称供电的实际工况,分析了磁动势空间运动轨迹以及不同区间磁动势的变化规律.文献[15]采用解析法设计了一种用于分析直线感应电机磁动势分布的数学模型,并基于此模型求取了电机的推力、效率、功率因数等基本性能.文献[16]根据不同的绕组排列方式,分析了合成磁动势基波的时间和空间特性,用以提高直线感应电机的运行效率.
为了准确计算绕组磁动势对电机性能的影响,国内外学者对磁动势谐波进行了相关研究.针对分数槽集中绕组磁动势谐波含量大的问题,文献[17-18]通过改变定子槽深、绕组分布、齿槽结构等方法降低了磁动势谐波含量,提高了电机效率.文献[19]采用在绕组中注入谐波电流的方法,用以减小绕组磁动势谐波含量,进而减小电机的转矩脉动.文献[20]计算了直线感应电动机的谐波磁动势分布,确定了磁动势高次谐波值等于零或显著降低的条件,提高了电磁推力.
电机绕组形式不同时,磁动势波形及其谐波含量均不相同,为了探究不同谐波含量的磁动势对电机推力特性的影响,本文作者在保证绕组磁动势安匝数一致的情况下,设计了3 种绕组形式(42 槽双层整距绕组、41 槽双层短距绕组、36 槽单层整距绕组)的短初级DLIM,计算了3种绕组产生的磁动势.在考虑谐波磁动势的前提下,推导出电磁推力的解析表达式,计算出考虑谐波磁动势时的平均推力.最后建立了有限元仿真模型,对电机的推力特性进行计算和分析,用以验证解析结果的正确性.
1 短初级双边直线电机绕组磁动势
1.1 绕组形式
绕组作为电机的重要组成部件,只有分析绕组的构成及连接方式,才能更好地研究电机的工作原理及运行特性.交流电机绕组有多种形式,并且可以采用多种标准进行分类.根据电机相数,可以分为单相及多相绕组;根据每极每相槽数,可以分为整数槽和分数槽绕组;根据槽内绕组层数,可以分为单层和双层绕组;单层绕组又可分为链式绕组、同心式绕组、交叉式绕组等;双层绕组又可分为叠绕组和波绕组.图1给出了短初级DLIM 常用的三种绕组类型和单边初级铁心模型,其中(a)为7 极42 槽双层整距绕组、(b)为7 极41 槽双层短距绕组、(c)为6 极36 槽单层整距绕组,它们的等效极数均为6.
1.2 磁动势分布
与旋转电机类似,直线感应电机通入三相对称电流时,将产生正弦分布沿着运动方向向前推移的行波磁场,在磁场和次级涡流的作用下,产生推力,而气隙磁场由磁动势产生,因此磁动势的分布情况会影响电机的推力性能.
以各项参数如表1 所示的3 种短初级DLIM 为研究对象,电机绕组采用分布式结构,每极每相槽数为2.
42、41 槽绕组两端半填充槽中的导体数为66,中间全填充槽中的导体数为132,36 槽单层绕组的每槽导体数为132.以上3 种电机绕组的每相串联匝数一致,3 种绕组的合成磁动势安匝数相同.在绕组中通入式(1)所示的三相交流电源.
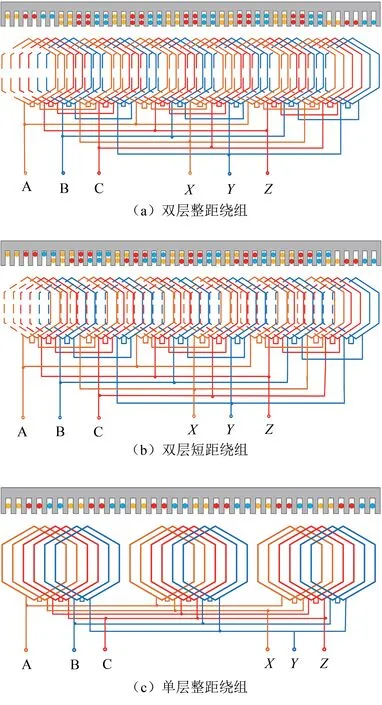
图1 绕组连接方式Fig.1 Winding connection types

表1 电机种类Tab.1 Motor types

在ωt=0°时,以B、C 相磁动势幅值为基值,得到3 种绕组各相磁动势和合成磁动势的标幺值分布如图2、图3 所示,并以运动方向上初级第1 个槽的中心为横轴坐标原点.

图2 三相磁动势分布Fig.2 Three-phase magnetomotive force distribution
由图2 可得,沿着初级x方向,三相磁动势波形为矩形波且各不相同.在ωt=0°时刻,A 相绕组磁动势幅值是B、C 相绕组磁动势幅值的2 倍.同理,当ωt分别为120°、-120°时,B、C 相磁动势幅值将达到最大且为另外两相的2 倍.
合成磁动势分布如图3 所示,其中双层整距、双层短距、单层整距绕组的磁动势幅值分别为4、3.5、4.由于短距绕组上下两层导体产生的磁动势存在抵消作用,导致其合成磁动势幅值低于整距绕组的合成磁动势幅值;因为绕组的每槽导体数相同,所以两种整距绕组的合成磁动势幅值也相等;根据图3(a)、(b)可得,双层绕组两端存在半填充槽,导致绕组两端的磁动势波形发生畸变,从而使绕组中部的磁动势对称分布,而两端磁动势则呈不对称分布;单层绕组不存在半填充槽,其磁动势波形在任意位置均为对称分布,如图3(c)所示.

图3 合成磁动势分布Fig.3 Synthetic magnetomotive force distribution
对三相合成磁动势进行谐波分解,得到其各次谐波幅值分布如图4 所示.42 槽和41 槽等双层绕组由于两端存在半填充槽、极数为7,导致其合成磁动势并非完全呈周期性变化,且谐波分解后主要存在3、4 次谐波(42、41 槽绕组3、4 次谐波的合成磁动势相当于其基波磁动势)以及在3、4 次谐波附近的低次谐波,除此之外,还含有38、39、44、45 等高次谐波;36 槽单层整距绕组的磁动势主要分解为3 次谐波(此时36 槽绕组的3 次谐波磁动势相当于其基波磁动势),还包括33、39 等高次齿谐波.按照上述的分解方法,下文所述的“基波磁动势”即为42 和41 槽绕组3、4 次谐波的合成磁动势或36 槽绕组的3 次谐波磁动势.

图4 谐波幅值分布Fig.4 Harmonic amplitude distribution
结合图4 分析,由于双层绕组存在半填充槽,合成磁动势波形两端发生畸变,导致其谐波含量多于单层绕组的谐波含量;另外由于短距绕组的节距为5τ/6(τ为极距),具有削弱高次谐波的作用,因此41 槽双层短距绕组的谐波含量低于42 槽双层整距绕组的谐波含量.

图5 磁动势波形分解Fig.5 Magnetomotive force waveform decomposition
为了对比分析考虑不同次谐波时磁动势的波形分布,图5 给出了三种绕组各次谐波的总合成磁动势、3 至4 次谐波合成磁动势或3 次谐波磁动势(基波磁动势)、1 至6 次谐波合成磁动势的分布情况.其中绕组为36 槽单层整距时,由于磁动势低次谐波含量较少,所以3 次谐波磁动势波形与1 至6 次谐波磁动势波形重合.绕组为双层整距和双层短距时,考虑1至6 次谐波的磁动势波形要更接近于原始阶梯形波.
2 电磁场求解
2.1 模型建立
在考虑谐波磁动势的情况下,对电机进行解析计算.以初级铁心为静止参考坐标系的短初级DLIM 的数学模型如图6 所示,模型分为初级与次级耦合区域Ⅰ,无初级两端非耦合区域Ⅱ和区域Ⅲ.当电机气隙与极距的比值小于0.25 时,可采用一维场理论分析,计算结果完全满足精度要求[21].对于具有上述3 种绕组的直线感应电机,对其进行解析计算,为了便于分析,作如下基本假设:1)忽略横向边端效应;2)电流沿z轴方向流动;3)初级铁心的磁导率为无限大,不计铁心饱和,电导率为零;4)气隙长度为常数;5)次级沿x方向无限长,铁心y方向高度无限大.

图6 短初级DLIM 电机数学模型Fig.6 Mathematical model of short primary DLIM
利用电磁场理论进行一维场解析计算,将开槽的初级铁心用表面光滑的铁心替代,并依据磁动势相等原则,用一无限薄的电流层代替实际初级绕组电流,线电流密度幅值为
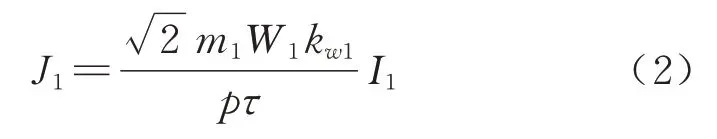

式中:L1为初级长度;y1为节距;q1为每极每相槽数;τn、φn、J1n分别为初级n次谐波的极距、初始相位、电密幅值;f为电流频率;ω为角频率.
为了便于计算,将线电流密度用复指数形式表示为

由于各次谐波的极距不同,n次谐波移动的滑差率为



2.2 边界条件

式 中:M1n、N1n、P1n、Q1n、M2n、N2n、P2n、Q2n的 解 析 式如下

因此可根据式(16)、式(17)、式(18)得到耦合区域(0<x<L1)气隙磁密、电场强度、次级电密的表达式.非耦合区域的气隙磁密可由式(20)求得,根据▽×H=J,得到区域Ⅱ、Ⅲ的电流密度解析式,如下

2.3 推力计算
通有三相对称正弦电流源的短初级DLIM,依据洛伦兹力公式,其平均电磁推力Fem可由次级电流层线密度j2的共轭和气隙磁密By乘积取积分得到.电机稳态运行时的推力表达式为

由2.2 节解析计算可得,次级电密和气隙磁场均为分段函数,次级电密可分为耦合区域电密j21、入端非耦合区域电密j22、出端非耦合区域电密j23,因此,电磁推力的解析式可用式(28)表示.Fem1、Fem2、Fem3分别为各个区域产生的电磁推力.
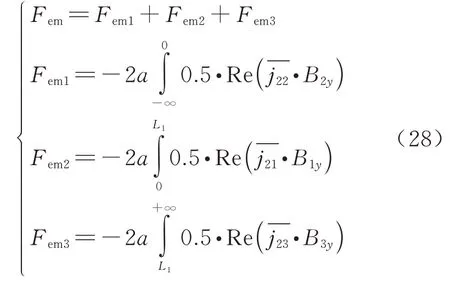
电机在实际运行时,非耦合区的气隙磁密较小,其产生的电磁推力相对于耦合区域的推力而言可以忽略不计.因此电磁推力可由耦合区域中各次谐波产生的推力叠加而成,其解析式为

3 推力特性验证
根据上一节得到的推力表达式,计算不同频率下考虑磁动势谐波时的推力特性曲线.并建立有限元模型,比较解析法与有限元法计算得到的推力大小,验证解析计算的正确性.
3.1 同一绕组考虑不同次谐波的推力
首先验证谐波磁动势对电机推力的影响.根据1.2 节磁动势分解结果,针对上述3 种绕组形式,分别解析计算不同频率下,仅考虑基波磁动势(42 槽、41 槽绕组的基波磁动势为3、4 次谐波的合成磁动势,36 槽绕组的基波磁动势为3 次谐波磁动势)时的电磁推力和考虑各次谐波磁动势时的电磁推力,并比较分析两种情况下得到的推力值.
图7 为解析计算得到的短初级DLIM 的推力特性曲线,结合图7 分析,比较不同工况下谐波磁动势S对推力的影响.当电机工作在临界转速时,仅考虑基波磁动势和考虑各次谐波磁动势,两种情况下计算得到的推力值相差最大,因此在临界转速时谐波磁动势对推力的作用最明显;当速度高于临界转速时,电机处于稳定运行状态,两种情况下计算的推力曲线近似重合,可得在稳态时谐波磁动势对推力的影响较小;速度低于临界转速时,电机处于不稳定状态,42、41槽双层绕组的电机考虑谐波磁动势后产生的推力高于只考虑基波时产生的推力,谐波磁动势产生有利于电机运动的推力.36槽单层绕组的电机在考虑谐波磁动势后产生的推力低于只考虑基波时产生的推力,此时谐波磁动势产生阻碍电机运动的制动力.
随着工作频率的增加,三种绕组的电机计算得到的最大电磁推力均略有降低,堵动时的推力呈下降趋势.整体来看,虽然各个绕组产生的谐波含量不同,但在只考虑基波磁动势和考虑谐波磁动势两种情况下,推力差值最大均不超过5 N,误差在6%以内.由此可得,谐波磁动势在一定程度上可以影响推力大小,在轨道交通等大推力控制精度要求高的场合,需要考虑谐波磁动势产生的电磁推力.
3.2 不同绕组推力解析与仿真结果对比

图7 磁动势谐波作用下的推力曲线Fig.7 Thrust curves under harmonic MMF
为了验证解析计算的正确性,通过有限元软件建立短初级DLIM 的仿真模型,图8 为42 槽双层整距绕组的二维有限元模型.绕组中通入有效值为6.85 A,频率为60 Hz 的三相对称正弦电流,仿真计算3 种电机不同工况下的平均推力.采用1~6 次谐波磁动势解析计算不同滑差下的电机推力,并比较有限元法与解析法计算得到的平均推力值.

图8 有限元仿真模型Fig.8 Finite element simulation model
图9 为采用两种方法计算得到的平均电磁推力随滑差率的变化曲线,所有推力曲线的变化趋势保持一致.为了验证磁动势波形对推力的影响,针对3 种不同绕组形式的电机,分别比较解析法和有限元法计算得到的3 条推力曲线.首先对比解析法得到的3 条曲线:当滑差率在0 至临界值时,电机处于稳定运行状态,双层整距绕组的电机产生的推力最大.根据式(29)分析,由于整距绕组的磁动势幅值高于短距绕组的磁动势幅值,且42 槽双层绕组的初级长度大于36 槽单层绕组的初级长度,所以42槽整距绕组的电机产生的推力略高于其他两种电机产生的推力;当滑差率大于临界值时,电机处于不稳定运行状态,推力随滑差的增大逐渐减小,此时36槽单层整距绕组的电机产生的推力略高于其他两种电机产生的推力.接着比较有限元仿真得到3 条推力曲线:在滑差率未达到临界值之前,3 条推力曲线的吻合程度较好,说明当电机处于稳定状态时,在保证磁动势安匝数相同的情况下,磁动势波形分布对推力的影响较小,3 种绕组形式的电机产生的推力近似相同;滑差率大于临界值时,推力的大小与磁动势波形的正弦性成正比,此时36 槽单层整距绕组的电机产生的推力最大.

图9 稳态推力曲线Fig.9 Steady thrust curves
为了验证解析法的正确性,针对同一绕组形式的电机,比较两种方法计算的推力曲线.由于解析计算时初级电流采用等效电流层替代、铁心磁导率近似为无限大,导致电磁推力的解析值与有限元仿真值存在一定的误差,滑差率为0 时,两种方法计算得到的误差较大.滑差率在0 至临界值时,稳定运行状态下的电机由两种方法计算的推力偏差低于7 N,误差在8%以内.在精度要求不高的情况下,可以近似认为两种方法得到的推力相同,两种方法具有较好的一致性,有限元法充分验证了解析理论的合理性,保证了解析结果的正确.
4 结论
1)双层绕组含有半填充槽,相较于无半填充槽的单层绕组,其合成磁动势中谐波含量较多,磁动势波形正弦性较差;由于短距绕组具有削弱谐波的作用,其磁动势波形中谐波含量少于整距绕组.
2)7 极双层绕组的合成磁动势分解后主要包含3、4 次谐波,6 极单层绕组的合成磁动势分解后主要包含3 次谐波.当电机工作在稳定状态时,谐波磁动势对推力的影响较小;当电机工作在非稳定状态时,双层绕组的谐波磁动势可以产生有利于电机运动的推力,单层绕组的谐波磁动势产生阻碍电机运动的制动力.谐波磁动势可影响推力大小,且不同次谐波对电机推力的作用不同.
3)解析法计算的推力大于有限元法计算的推力.电机工作在稳定状态下,解析计算时双层整距绕组的电机产生的推力最大,有限元法计算时3 种绕组的电机推力近似相同;电机工作在非稳定状态下,单层绕组的电机产生的推力最大,整距绕组电机产生的推力高于短距绕组电机产生的推力.
参考文献(References):
[1]叶云岳. 直线电机原理与应用[M]. 北京:机械工业出版社,2000.
YE Yunyue. Principle and application of linear motor[M].Beijing:China Machine Press,2000.(in Chinese)
[2]龙遐令. 直线感应电动机的理论和电磁设计方法[M].北京:科学出版社,2006.
LONG Xialing. Theory and method of electomagnetic design for linear induction motors[M]. Beijing:Science Press,2006.(in Chinese)
[3]邸珺,范瑜,刘亚静. 基于等效次级的直线感应电机的电磁分析与参数辨识[J]. 电工技术学报,2017,32(11):145-154.
DI Jun,FAN Yu,LIU Yajing.Electromagnetic analysis and parameter estimation for the linear induction motor based on equivalent secondary[J]. Transactions of China Electrotechnical Society,2017,32(11):145-154.(in Chinese)
[4]宫金林,王秀和. 基于多目标有效全局优化算法的直线感应电动机优化设计[J]. 电工技术学报,2015,30(24):32-37.
GONG Jinlin,WANG Xiuhe. Optimal design of a linear induction motor using multi-objective efficient global optimization[J]. Transactions of China Electrotechnical Society,2015,30(24):32-37.(in Chinese)
[5]杨通. 高速大推力直线感应电机的电磁理论与设计研究[D].武汉:华中科技大学,2010.
YANG Tong. Theoretical study and electromagnetic design for high-speed and high-thrust linear induction motor[D].Wuhan:Huazhong University of Science and Technology,2010.(in Chinese)
[6]王江波,李耀华,严陆光. 长初级双边直线电机高性能控制策略[J].电工技术学报,2011,26(5):126-131.
WANG Jiangbo,LI Yaohua,YAN Luguang. High performance control strategy for long primary double sided linear motors[J]. Transactions of China Electrotechnical Society,2011,26(5):126-131.(in Chinese)
[7]BIAN F F,ZHAO W X,JI J H,et al. Mechanism investigation of ring type winding in linear permanent magnet vernier machine for improving force density[J]. IEEE Transactions on Vehicular Technology,2020,69(3):2588-2597.
[8]HAN Z Q,XU J,RUI W Z,et al. Effect of winding connections on thrust and current asymmetry of linear induction machines considering end effect[J]. IEEE Transactions on Plasma Science,2020,48(8):2816-2821.
[9]梅威虎,卢琴芬. 一种新型双层绕组无铁心永磁直线电机的优化设计[J].微电机,2019,52(5):1-5.
MEI Weihu,LU Qinfen. Optimization design of a novel double-layer winding ironless permanent magnet linear motor[J].Micromotors,2019,52(5):1-5.(in Chinese)
[10]WANG S P,WANG Y H,LIU C C,et al. Comparative study of linear superconductivity machine with different dtator and winding configurations[J]. IEEE Transactions on Applied Superconductivity,2019,29(2):1-4.
[11]LIU C C,WANG D Y,WANG S P,et al. Design and analysis of a new permanent magnet claw pole machine with s-shape winding[J]. IEEE Transactions on Magnetics,2021,57(2):1-5.
[12]汤蕴璆.电机学[M].5 版.北京:机械工业出版社,2014.
TANG Yunqiu. Electric machinery[M]. 5th ed. Beijing:China Machine Press,2014.(in Chinese)
[13]程恳,程小华. 交、直流电机绕组磁动势求取方法之比较[J].防爆电机,2016,51(6):1-3.
CHENG Ken,CHENG Xiaohua. Comparison of solving methods between winding MMFs of AC machine and DC machine[J].Explosion-Proof Electric Machine,2016,51(6):1-3.(in Chinese)
[14]董锋斌,皇金锋. 三相交流电动机不对称供电工况下磁动势的变化规律[J]. 陕西理工大学学报(自然科学版),2020,36(4):25-29.
DONG Fengbin,HUANG Jinfeng. Variation law of magnetic motive force of the three-phase AC motor under the condition of asymmetric power supply[J]. Journal of Shaanxi Shaanxi University of Technology(Natural Science Edution),2020,36(4):25-29.(in Chinese)
[15]LYU G,ZENG D,ZHOU T. A novel MMF distribution model for 3-D analysis of linear induction motor with asymmetric cap-secondary for metro[J]. IEEE Transactions on Magnetics,2017,53(9):1-7.
[16]ZHOU D J,MA J Q,ZHAO L F,et al. The time and space characteristics of magnetomotive force in the cascaded linear induction motor[J]. Journal of Modern Transportation,2013,21(3):194-199.
[17]段谟海,林荣文.基于分数槽集中绕组永磁电机的绕组磁动势谐波优化[J].电气开关,2020,58(6):14-17.
DUAN Mohai,LIN Rongwen. Optimization of winding MMF harmonics based on fractional slot concentrated winding permanent magnet motor[J]. Electric Switcher,2020,58(6):14-17.(in Chinese)
[18]郑军强,赵文祥,吉敬华,等. 分数槽集中绕组永磁电机低谐波设计方法综述[J]. 中国电机工程学报,2020,40(增1):272-280.
ZHENG Junqiang,ZHAO Wenxing,JI Jinghua,et al.Review on design methods of low harmonics of fractional-slot concentrated-windings permanent-magnet machine[J]. Proceedings of the CSEE,2020,40(S1):272-280.(in Chinese)
[19]ZHANG M,WU Y,SUN L,et al. Torque ripple reduction of a doubly salient electromagnetic machine using harmonic current injection with optimized magnetomotive force[C]// IEEE 9th International Power Electronics and Motion Control Conference.Beijing,2020:2247-2253.
[20]PERNEEL L,FAYYAD-KAZAN H,TIMMERMAN M,et al. The harmonic structure of the magnetomotive force of the linear induction motor with transverse magnetic flux[J]. International Journal of Theoretical and Applied Mechanics,2018,13(1):61-72.
[21]上海工业大学,上海电机厂. 直线异步电动机[M]. 北京:机械工业出版社,1979.
Shanghai University of Technology,Shanghai Electric Machinery Factory. Linear induction motor[M]. Beijing:China Machine Press,1979.(in Chinese)

