基于Sepic的单开关高增益DC/DC变换器

赵世伟，高双，丁杰

(华南理工大学 电力学院，广州 510000)

0 引 言

近年来，随着可再生能源在分布式系统的不断应用与发展，高增益DC/DC变换器在直流母线与微源之间得到了广泛应用。直流微网母线的总线电压一般需要达到220 V或380 V，某些应用场合中会要求达到400 V[1-2]。然而以光伏电池、燃料电池为代表的多种微源只能输出较低的直流电压，因此研究高增益直流变换器在这些系统中的应用有着重要的实际意义。

非隔离电流型DC/DC变换器由于具有输入电流连续、低纹波、低成本和结构简单等优点而被广泛应用于高压场合中。传统拓扑如Boost,Sepic等，在占空比接近100%时，理论上电压增益会达到无限大。当占空比过大时，电路的效率会下降，整个系统的闭环控制稳定性能会变差，并且还会导致开关管和二极管上的高电压应力，因此电压增益一般最高为5倍。然而在实际的应用中，一般期望变换器的电压增益大于或者等于10倍[3]。为进一步提高变换器电压增益，将一些升压技术与经典的变换器拓扑相结合可以得到较高的电压增益，如开关电容与开关电感结合、耦合电感与开关电容结合、交错并联技术等[4-6]。

在光伏并网应用系统中，为了能够实现最大功率点跟踪，一般要求变换器具有连续的输入电流，以便调节其输出功率。文献[7]通过在耦合电感Boost变换器上额外增加两对电容和二极管，实现了更高的电压增益，但是输入电流不连续，不利于光伏并网系统实现MPPT功能，并且二极管反向恢复问题严重。文献[8-9]中利用耦合电感与开关电容相结合的技术使得变换器的输出电压与输入电压之间的比值提高。然而，因为耦合电感漏感的原因，MOS管在断开的的时候其两端会产生较高的电压尖峰，降低了系统的效率和可靠性。文献[10]中增加了无源箝位电路来降低开关管关断过程中产生的过电压。但是这样做在某些情况下会使得输入电流不连续，对实际应用不利。在文献[11-13]中，有学者已经提出了基于Sepic的高增益变换器，但是这些变换器的电压增益均较低。经典的Sepic变换器在输入端连接有电感，因此输入电流纹波会降低，可以减弱电路的EMI效应[14]。本文提出一种基于Sepic的新型高增益DC/DC变换器，如图1所示。保留Sepic变换器优点的同时，还极大的提高了变换器的电压增益，与文献[15-17]中所提出的变换器相比电压增益有了明显提高。文中对变换器在稳态时的工作过程进行详细分析，推导出各个开关器件的电压、电流应力表达式，提供磁性器件参数的计算公式。最后搭建一台200 W的样机，测试出来的实验结果证明所提变换器的有效性。

1 变换器电路原理

1.1 电路拓扑

提出了一种具有高升压比且输入电流连续的DC/DC变换器。将不同的升压方式进行组合，使得该变换器实现了高电压增益特性、并且由于输入端电感的存在，其输入电流是连续的，其电路结构图如图1(a)所示，将耦合电感等效为理想变压器与励磁电感并联后再与漏感串联，匝比为N=NS/NP，励磁电感为Lm，漏感为Lk。假设变换器工作在电感电流连续模式，因此为简化讨论其工作原理，考虑下列假设：

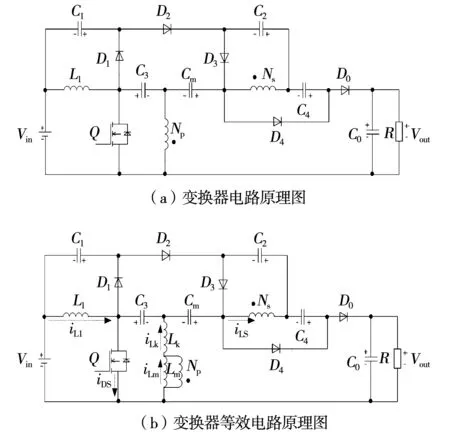
图1 所提变换器电路原理图Fig.1 Schematic diagram of the proposed converter circuit

1)功率开关器件均是理想的，且不考虑发生在上面的功率损耗；

2)电感、电容均为理想型器件，寄生效应忽略不计，且所有的电容足够大，电容上的电压可看做是恒定值；

3)耦合电感的耦合系数K=Lm/ (Lm+Lk)，匝比N=Ns/Np。

1.2 工作原理分析

变换器稳定工作时，在一个开关周期内的波形如图2所示。

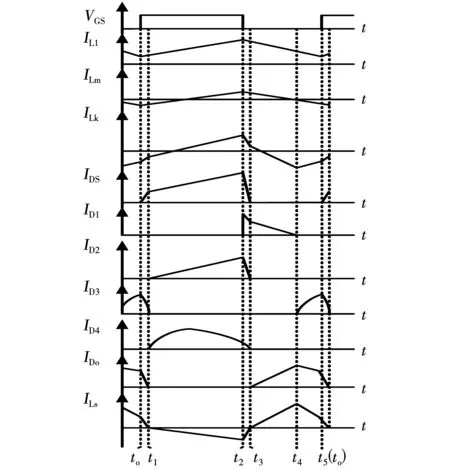
图2 变换器的主要工作波形Fig.2 Main working waveform of the converter

当变换器工作在连续导通模式时，可以看出其在一个开关周期内可分为5种开关模态。励磁电感电流ILk、漏感电流ILk、次级绕组电流ILs三者之间的关系表达式为

(1)

各个开关模态的电路结构图如图3所示。

开关模态1[t0-t1](如图3(a))：在这个工作过程中，开关管Q在t=t0时刻导通，二极管D1、D2、D3、D4均截止，输出二极管D0导通。开关管两端电压VDS开始下降，输入电流Iin与初级绕组的漏感电流均开始上升，耦合电感次级绕组的漏感开始释放能量。漏感两端电压的表达式为

(2)

由于漏感两端电压非常高，但是漏感值很小，因此漏感电流变化率会很大，模态1的时间很短。当初级绕组的漏感电流与励磁电流相等时，模态1结束。

开关模态2[t1-t2](如图3(b))：在这个工作过程中，开关管Q仍然保持导通。此时二极管D2、D4导通，二极管D1、D3截止。当漏感电流值超过励磁电感电流时，副边绕组的电流方向改变，二极管D4导通。直流电压源通过开关管Q对L1充电，电容C3通过开关管S对耦合电感的励磁绕组Lm和漏感Lk充电，同时耦合电感的副边绕组通过二极管D4给倍压电容C4充电，负载R的能量由输出电容C0提供。此时L1与Lm的电压关系为式(3)所示。

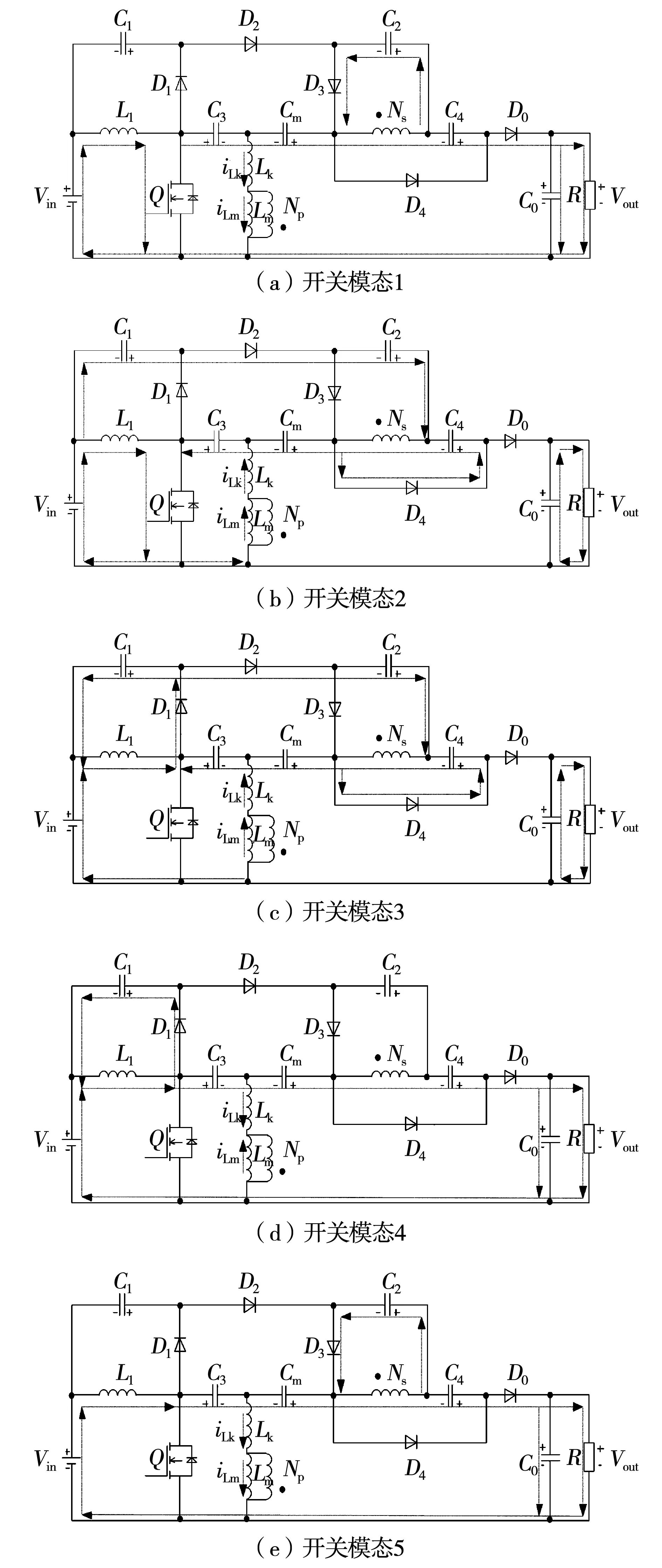
图3 变换器各个开关模态等效电路图Fig.3 Equivalent circuit diagram of each switch mode of the converter

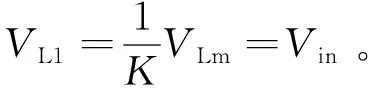
(3)

这个阶段的漏感两端电压、电流表达式为

(4)

式中ILk(t1)表示ILk在t1时刻的值，其他的依次类推。

开关模态3[t2-t3](如图3(c))：在这个工作过程中，开关管在t=t2时刻关断。流过电感L1的电流与初级绕组的漏感电流通过二极管D1对电容C1充电。耦合电感的副边绕组以及电容C2、C3通过二极管D2对倍压电容Cm充电，同时副边绕组在漏感的作用下继续通过D4向倍压电容C4充电，漏感电流逐渐减小。此时漏感两端电压的表达式为

(5)

由于漏感电流值比励磁电流值下降的更快，因此当耦合电感励磁电流与漏感电流下降到其值相等时，二极管D2关断，此时过程3结束。同理其持续时间也很短。

开关模态4[t3-t4](如图3(d))：在这个工作过程中，开关管Q仍然保持关断。电感L1通过二极管D1给电容C1充电。当初级绕组的漏感电流降低至与励磁电流相等时，次级绕组的电感电流方向改变，使得二极管D0导通。另外，直流电压源、电感L1、耦合电感的励磁绕组、倍压电容Cm、C4通过二极管D0向输出电容C0和负载R提供能量，同时也在给电容C3充电。此时L1与Lm两端的电压表达式为：

(6)

开关模态5[t4-t5](如图3(e))：在这个工作过程中，开关管Q依旧保持关断状态。直流电压源、电感L1、倍压电容Cm通过二极管D3向电容C2充电，与此同时，也和倍压电容Cm一起通过二极管D0向输出电容C0和负载R提供能量。

2 变换器稳态特性分析

2.1 电压增益

由于模态1和模态3的时间较短，为了简化分析，只选取模态2、模态4、模态5进行分析，并且假设所提变换器的工作模态处于CCM模式下。

当开关管Q开通时，根据图3(b)可以得到：

VC4=NVLm=NKVin，

(7)

VCm=VC1+VC2+NVLm+VC3+VL1。

(8)

当开关管Q关断时，根据图3(d)可以得到

V0=Vin+VCm+VL1+NVLm+VC4-VC3。

(9)

根据电感L1与Lm的伏秒平衡原理，联立式(3)、式(6)，有如下等式：

(10)

式中：D为开关管的导通占空比；TS为开关周期。

得到C1、C2两端的电压表达式为：

(11)

联立式(3)、式(8)、式(11)可以得到

(12)

联立式(6)、式(7)、式(9)、式(12)得到变换器的电压增益表达式为

(13)

当耦合电感系数K=1时，变换器的电压增益表达式为

(14)

当匝比N=1时，所提变换器与其他文献所提变换器、传统Sepic变换器之间的电压增益对此如图4所示。在占空比相同的的情况下，所提出的变换器电压增益的上升幅度远大于传统Sepic变换器以及文献[15-17]所提出的变换器。

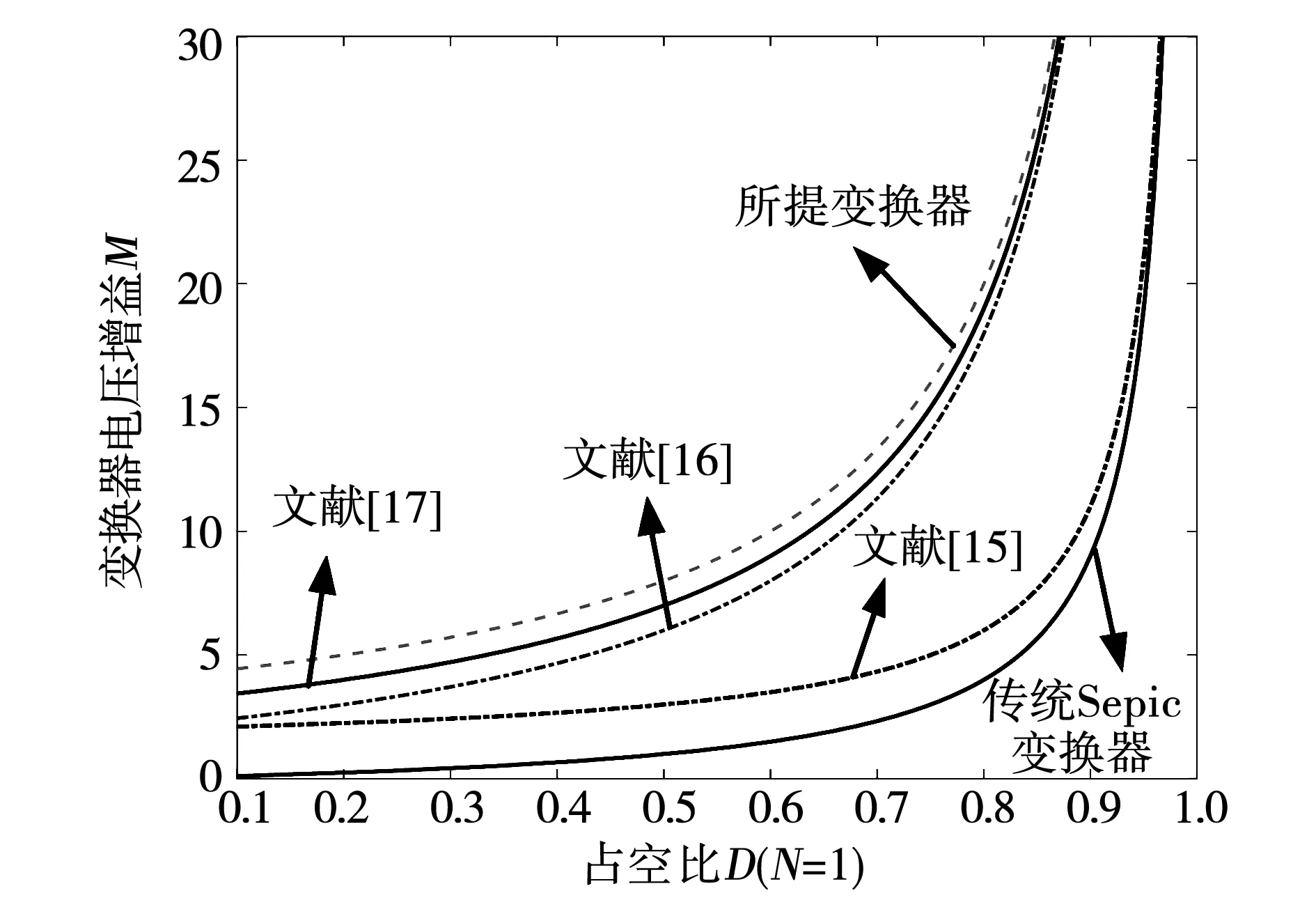
图4 不同变换器的电压增益与占空比之间的关系Fig.4 Relationship between voltage gain and duty cycle of different converters

给定匝比N=2，电压增益随占空比、耦合系数改变而变化的三维图形如图5所示。可以明显看出，当占空比值一定时，耦合系数的值越大，所对应的电压增益越大。

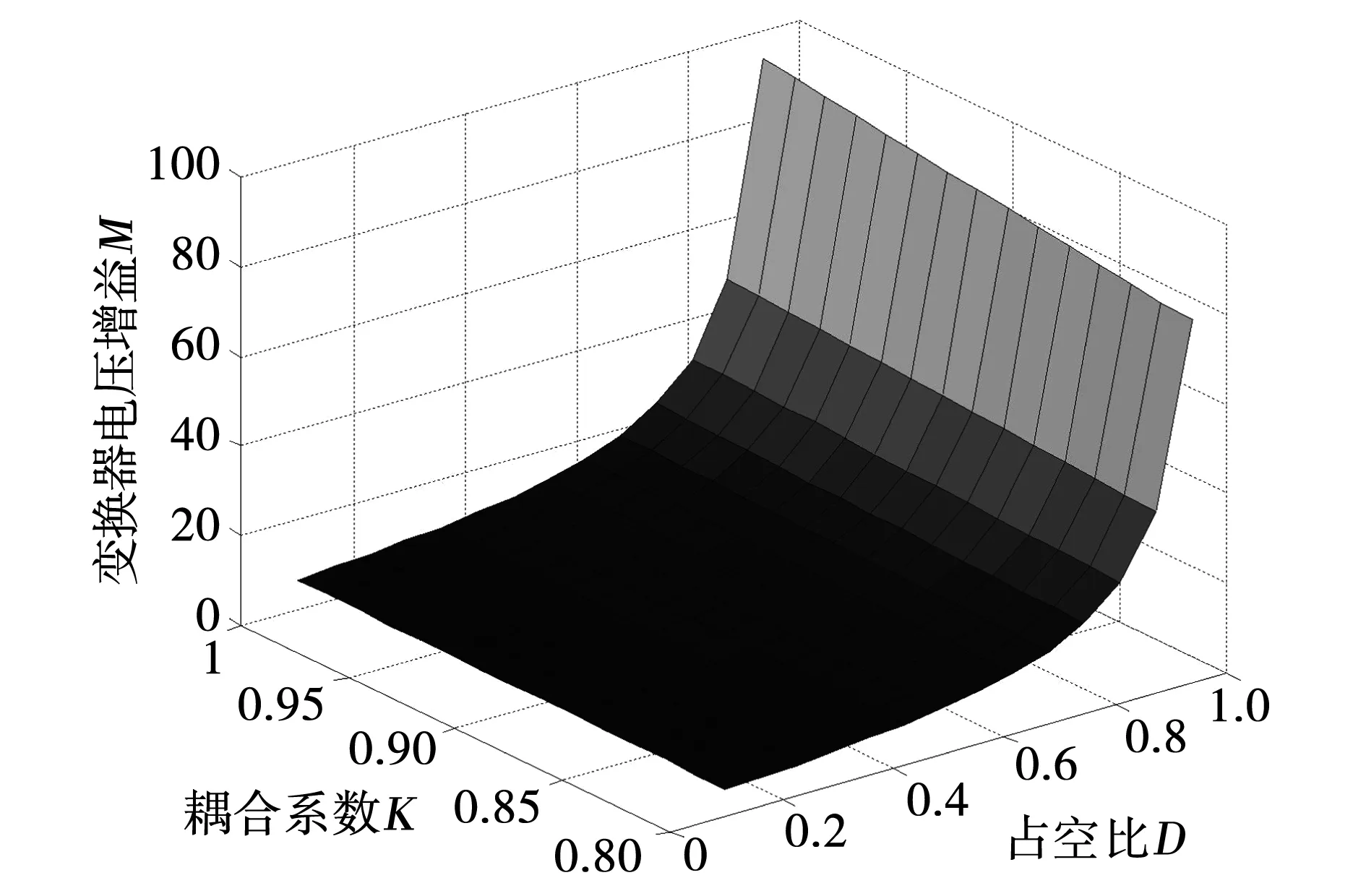
图5 变换器的电压增益与占空比D、耦合系数K之间的关系Fig.5 Relationship among the voltage gain, the duty cycle D and coupling coefficient K

图6给出了当输入电压Vin=30 V、匝比N=1的条件下，输出电阻负载值与占空比发生改变时，对变换器电压增益的影响关系曲线。从图中可以看出，本文所提出的变换器具有较好的带负载能力。

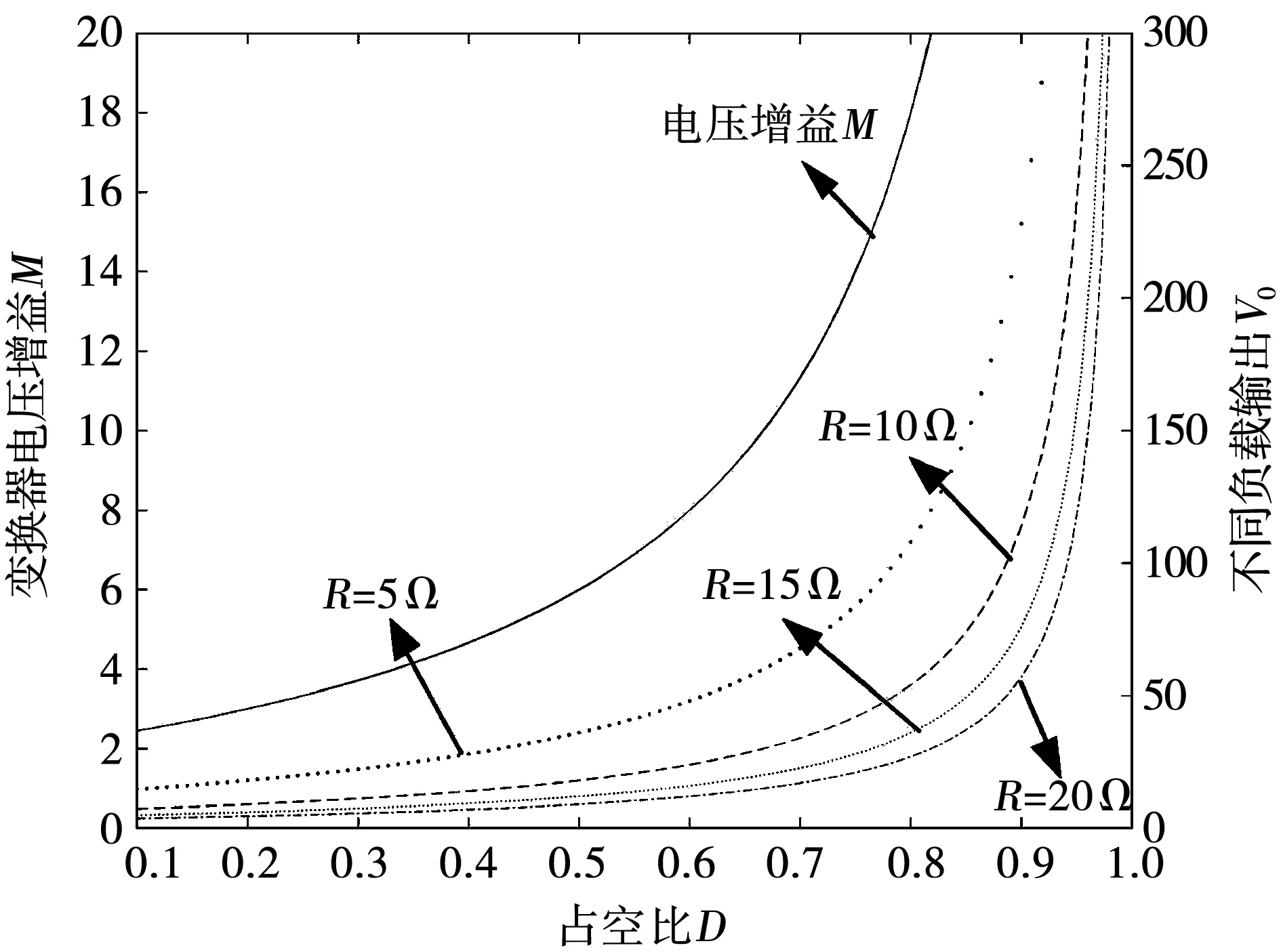
图6 变换器的电压增益与占空比D、不同负载输出之间的关系Fig.6 Relationship among the voltage gain, the duty cycle D and different load output

2.2 电压应力

为简化分析，设定耦合系数K=1，结合各个开关模态的等效电路图，可以得到该拓扑中所用器件的电压应力表达式。

有源开关管Q的电压应力为

(15)

二极管D1的电压应力为

(16)

二极管D2、D0的电压应力为

(17)

二极管D3、D4的电压应力为

(18)

电容C1、C2两端的电压应力分别为：

(19)

电容Cm两端的电压为

(20)

当K=1时，变换器中开关器件的电压应力与输出电压比值同耦合电感匝比之间的关系如图7所示。随着匝比的加大，二极管D3、D4的电压应力是随着匝比的增加而加大的，因此在实际电路设计时切勿将匝比N取得过大。

图7 耦合电感匝比N对功率器件电压应力的影响Fig.7 Influence of coupling inductor turns ratio N on voltage stress of power devices

2.3 电流应力

根据1.2节的分析以及电容的安秒平衡，易知流过二极管的电流平均值与输出电流I0值相等，结合图3可以得到以下等式：

(21)

流过二极管的电流峰值为：

(22)

忽略变换器工作过程中的功率损耗，得到输入电流的平均值表达式为

Pin=Pout⟹VinIL1=V0I0⟹IL1=MI0。

(23)

可得励磁电感电流的平均值为

DILm+(2N+1)I0=(1-D)IL1-I0⟹

ILm=0。

(24)

根据图3(c)可得，流过开关管的电流峰值为

IDS(peak)=IL1(peak)+ID1(peak)。

(25)

结合式(22)、式(23)、式(25)可得

(26)

式中fS为开关频率。

2.4 变换器性能分析

表1为本文所提出变换器与参考文献[15-17]变换器的部分特性对比。该表表明，虽然提出的变换器比文献[15]多了一个电感和电容、比文献[16-17]均增加了二极管和电容的数量，但是提出的变换器电压增益都明显高于这三种变换器，开关管和二极管电压应力也均明显的低于这三种变换器，可以选择VDS低、RDS(ON)小的开关管，能够降低功率器件上的传导损耗，提升变换器效率。由于提出的变换器存在输入电感，所以变换器的输入电流纹波值也会明显低于文献[15]所提的变换器。文献[16]比提出的变换器多了一个开关管和电感，增加了变换器的制作成本且不利于体积的小型化。

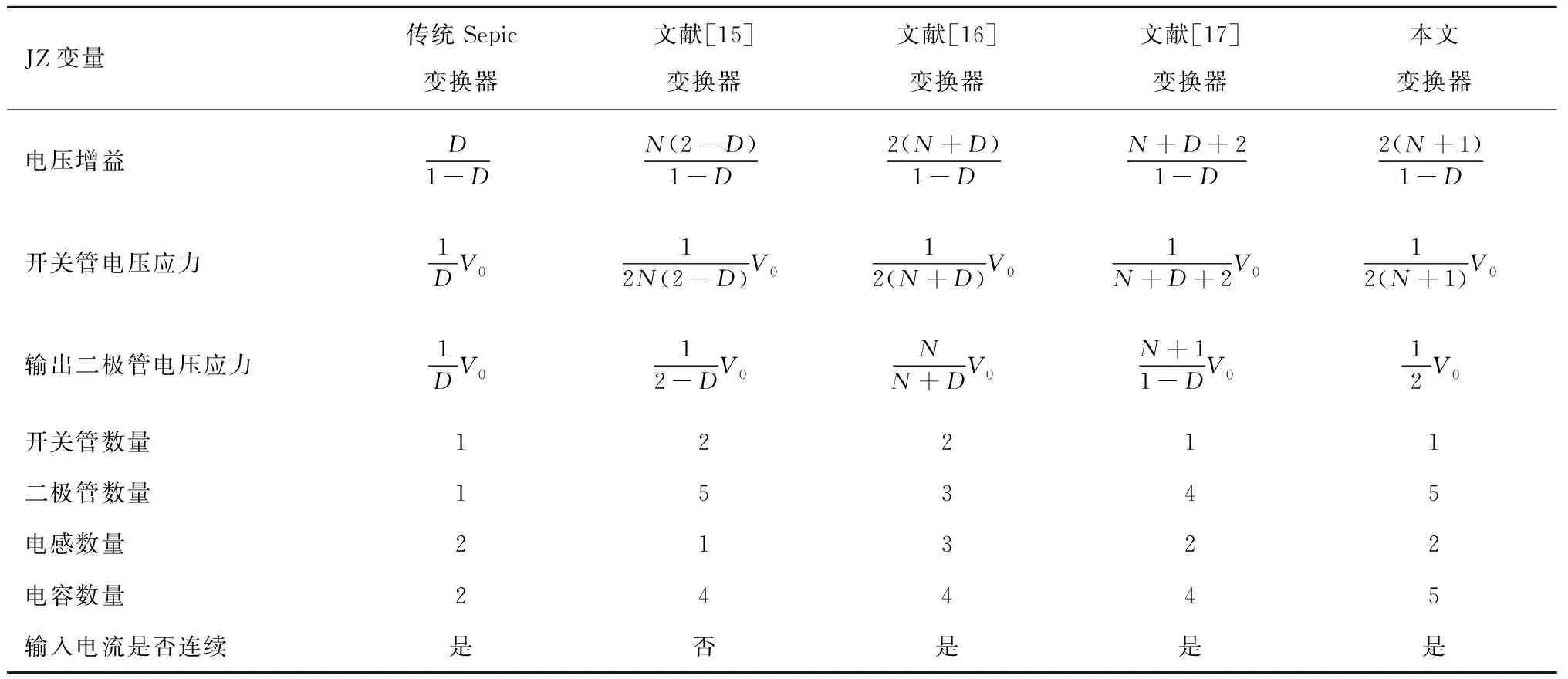
表1 所提出的变换器与其他变换器比较

3 变换器参数设计

3.1 电感参数设计

合适的元器件参数是保证变换器能够正常工作的条件。当变换器工作在电流断续模式时，会存在动态响应慢、二极管的电流应力大等缺点，因此本文所提出的变换器仅考虑在电流连续模式下工作。输入电感L1与励磁电感Lm的电流纹波值应该满足以下表达式：

(27)

如图3所示，输入电感电流与励磁电感电流在t0时刻达到最小值，在t2达到峰值，联立式(23)、式(24)、式(27)可得输入电感电流、励磁电感电流的最小值为：

(28)

因此为保证在整个周期内输入电感工作在电流连续模式下，即IL1(min)>0，其电感值L1应该满足

(29)

当流过输出二极管电流在开关管整个关断周期内不为零时，变换器满足输出电流连续的条件。根据图3(e)可得输出电流与输入电流、励磁电感电流满足以下关系式

(2N+1)ID0=IL1(min)+ILm(min)>0。

(30)

同理，联立式(28)、式(29)可得励磁电感值应该满足

(31)

3.2 电容参数设计

不计电容ESR的影响，为了将输出电压纹波控制在合理的值，电容值应该满足以下关系：

(32)

(33)

4 实验结果分析

为了验证理论分析的正确性与所提出的变换器的可行性，设计制作了一台200 W的实验样机，实验时的变换器规格与元器件参数如表2所示。

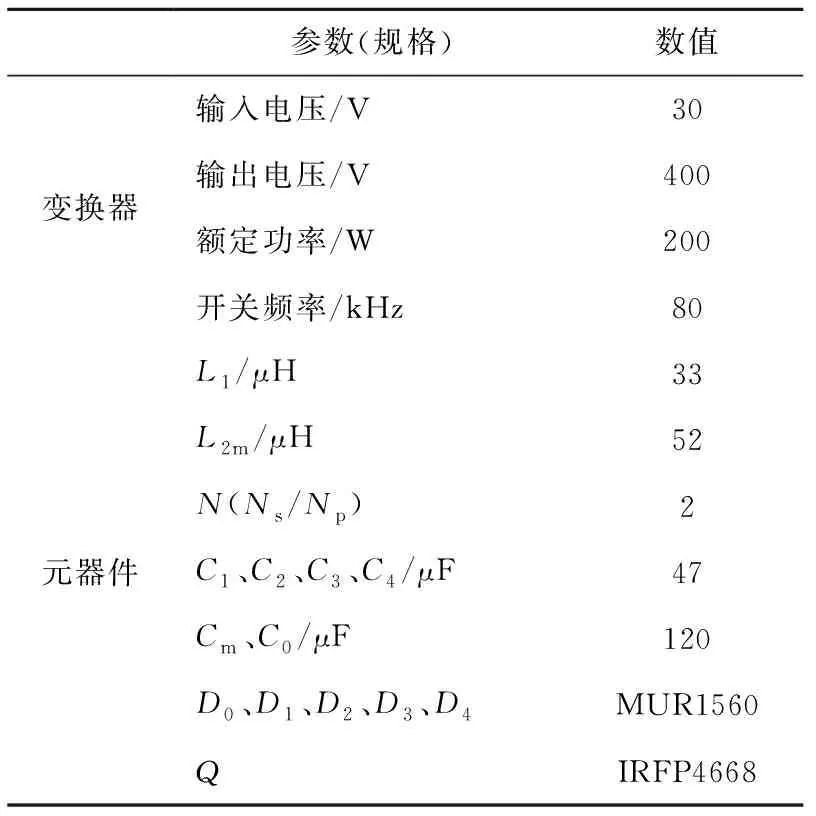
表2 所提变换器规格

开关管电流、电压波形如图8所示。显然，开关管关断期间的漏、源极电压的最大值约为输出电压的1/4，与传统的Sepic变换器相比开关管电压应力明显降低，并且从电流波形中可以看出，开关管接近实现了零电流开通，在一定程度上减小了开关损耗。

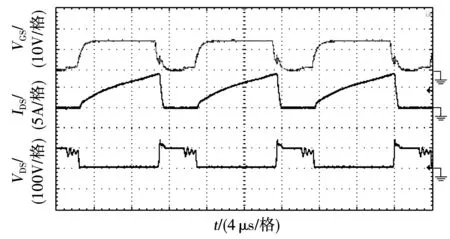
图8 开关管的电流、电压波形Fig.8 Switch current and voltage waveform

输入电流与耦合电感原、副边电流波形如图9所示。输入电流波形是连续的，其平均值约为7.2 A，耦合电感的原、副边电流波形与理论分析的基本吻合。

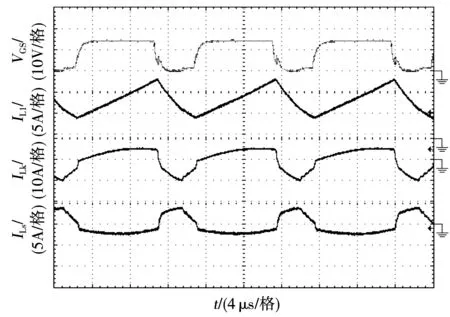
图9 输入电流与耦合电感原、副边电流波形Fig.9 Input current and coupled inductor primary and secondary current waveforms

二极管D1、D2、D4电压和电流波形如图10和图11所示。可以很明显的看到，二极管D1、D2的电压应力比D4的电压应力小，约为输出电压的1/4，而D4的电压应力约为输出电压的1/2。在开关模态2中，当开关管Q闭合时，漏感Lk与电容C3、Cm之间发生谐振，因此二极管D4的电流波形是非线性的，同时二极管均属于自然关断，不存在反向恢复的问题。

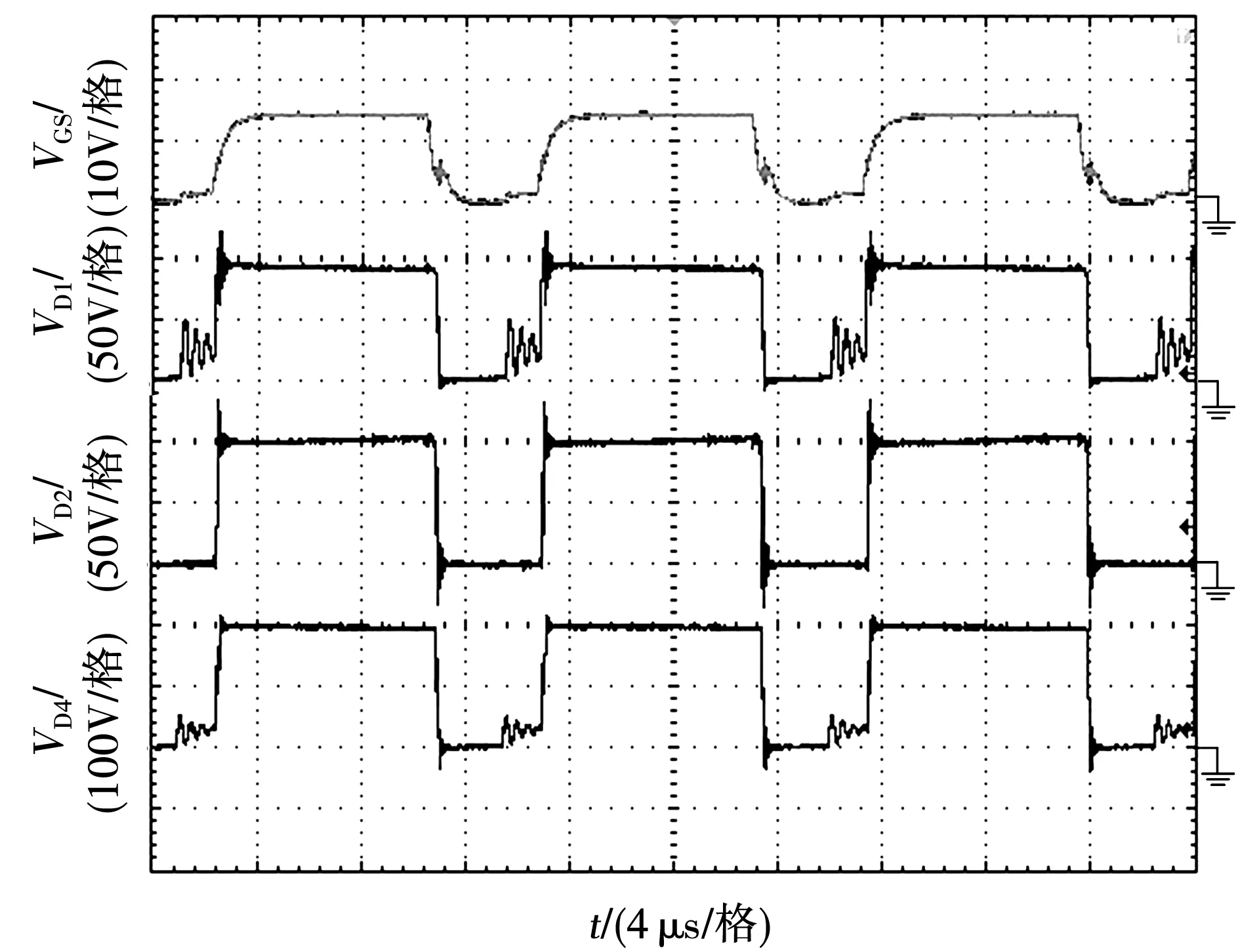
图10 二极管电压波形Fig.10 Voltage waveform across the diode

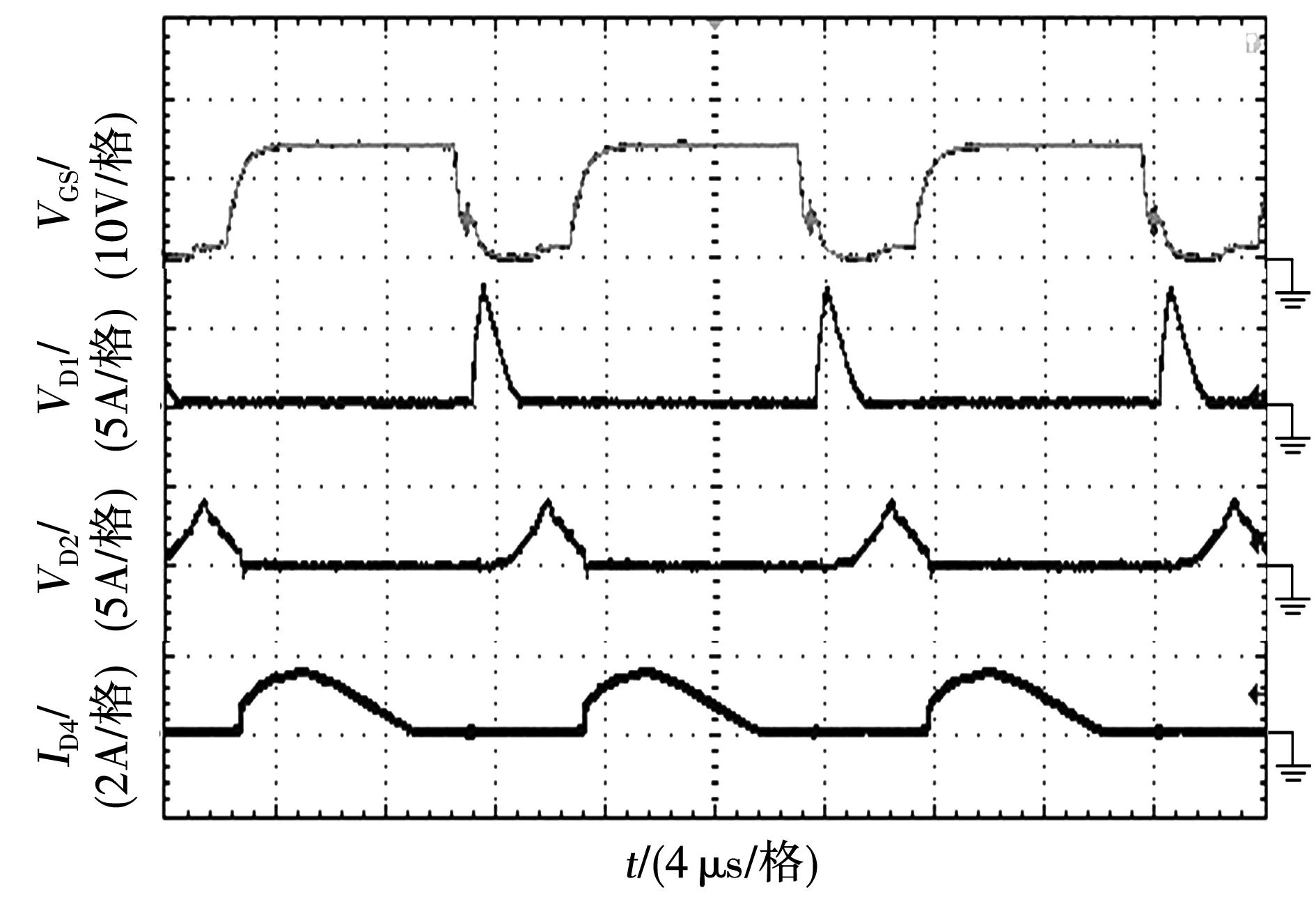
图11 二极管电流波形Fig.11 Current waveform across the diode

电容C1、C2、C4、Cm两端电压波形如图12所示。从图中可以看出，实验结果中电容两端电压的值与理论分析的大致相同。

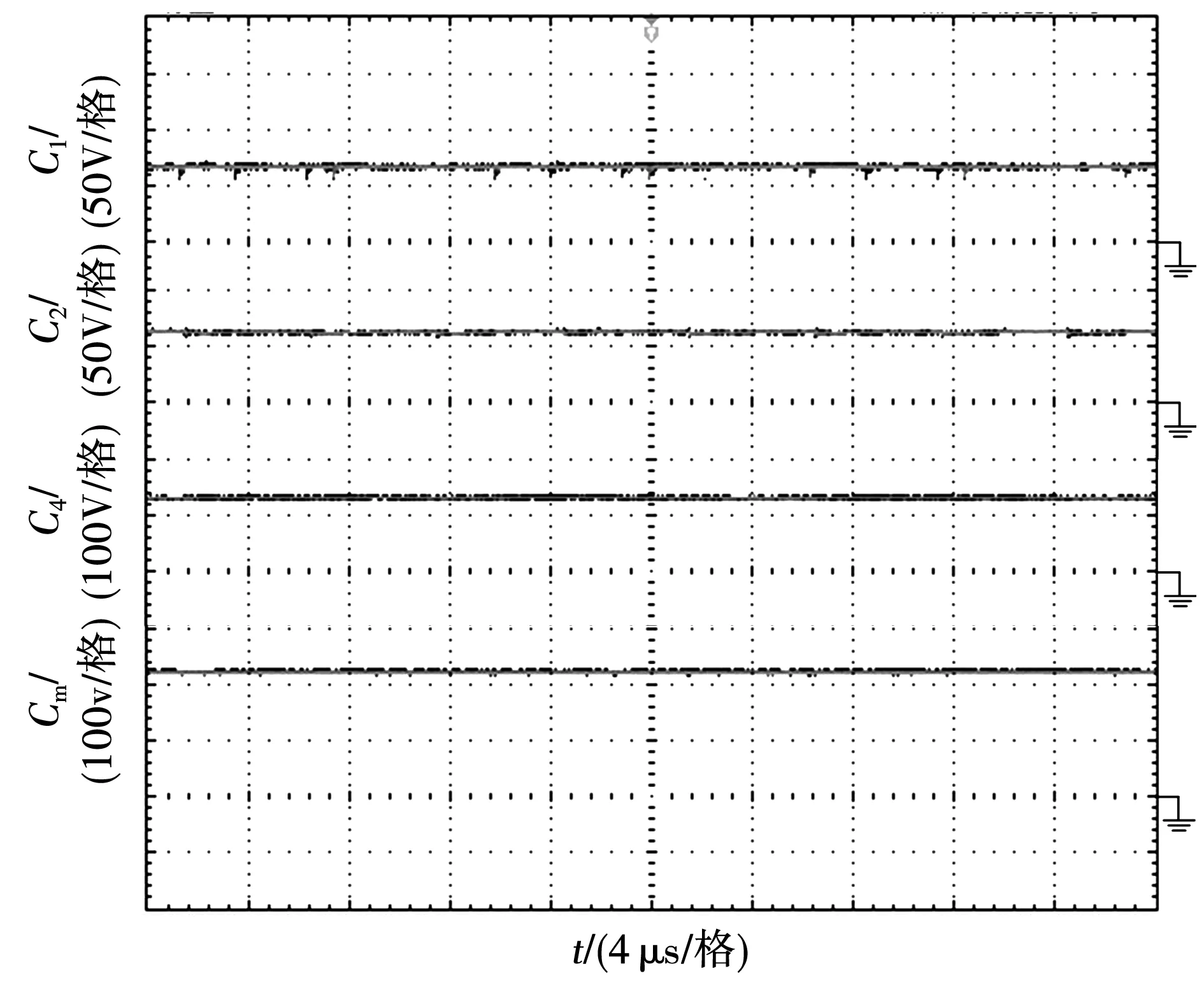
图12 电容C1、C2、C4、Cm两端电压波形Fig.12 Experimental waveforms of VC1、VC2、VC4、VCm

图13为变换器的效率曲线。从图中可以看出，设计的变换器样机在100 W时的效率最高，达到了92.3%。

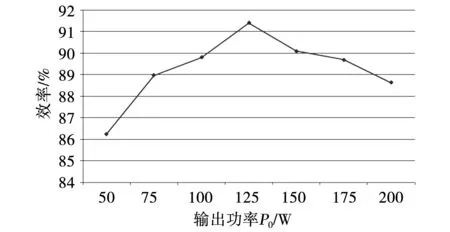
图13 效率曲线Fig.13 Efficiency curve

5 结 论

将开关电容、耦合电感两类倍压单元与传统Sepic变换器相结合，提出了一种新型的高升压比DC/DC变换器 。该拓扑结构具有较高的电压转换比、半导体器件电压应力低等优点。本文讨论了变换器在输入电流连续时的稳态工作情况，并且制作了一台200 W的样机，以验证该拓扑的有效性。测得的实验波形可知，本文提出的变换器具备下列特征：

1)将开关电容与耦合电感两类单元进行组合，在相同条件下，文中所提出的变换器得到的电压增益更高。由于耦合电感的存在，通过调整匝比N也可以提高电压增益比M。

2)开关器件的电压应力低，选择低耐压值、导通电阻小的开关器件，在节约成本的同时提升变换器的效率。

3)保留了Sepic变换器输入电流连续的特点，基本实现开关管的零电流开通，二极管的反向恢复问题较轻。

4)励磁电感是双向励磁，磁芯的利用率更高。