含风力发电的电动汽车充电站区间优化调度

程杉，杨堃，汪业乔，严潇，魏昭彬

(三峡大学 电力系统智能运行与安全防御宜昌市重点实验室，湖北 宜昌 443002)

0 引 言

考虑能源安全和环境保护，风力发电等清洁能源[1-2]和电动汽车(electric vehicle,EV)[3-4]已经在国内外大力推广发展。将EV通过充电站接入电网，对动力电池统一管理，可以有效缓解EV接入电网所带来的负面影响，就地消纳可再生能源，实现真正意义上的低碳，而含有分布式风力发电的EV充电站(charging station with distributed wind power generation,CS-DWPG)是实现的有效途径之一[5-6]。为满足EV的充电需求和CS-DWPG的经济效益，保障电网安全、稳定地运行，科学合理的CS-DWPG调度起着至关重要的作用，解决该问题的基础是实现对风力发电和EV充电负荷的有效预测。

学者们针对风电功率预测模型和算法进行了大量的研究。文献[7]提出了尤其适用于超短期预测的贝叶斯神经网络模型，但并不适用于中长期风电功率预测；文献[8]建立了基于均方根误差的组合预测模型，但由于需要确定各个子模型的权重系数，该模型将会加长预测时的数据处理时间；文献[9]提出了在某些特定气象条件下具有较高精确度和可靠性的基于贝叶斯模型平均和集成学习的确定性预测方法。考虑风速时间序列的非线性、不确定性和随机性以及点值模型的不足和区间算法的优点，文献[10]利用人群搜索算法的核极限学习机区间预测模型，能够快速获得预测区间，但优化时易陷入局部最优而导致预测结果不稳定；文献[11]建立了具有良好预测精确度的基于模糊聚类的区间预测模型，但隶属度函数的选取具有较强的主观性并且计算效率较低。

EV无序充电尤其是规模化接入还可能引起系统峰值负荷增长，进而对系统发电和输电能力造成压力[12]。而EV作为柔性负荷[13]，对其充、放电合理安排对配电网的负荷曲线具有良好的削峰填谷作用[14-17]，如文献[18]提出了基于事件驱动的EV优化调度策略，但该策略不适用于大规模EV入网时的优化调度问题；文献[19]提出了考虑EV充、放电的大规模集群实时优化调度模型。

实际上，无论是风电功率与EV充电需求预测及含风电和EV的电力系统优化调度，都需要考虑风电和EV入网随机性[20-21]所产生的不确定性问题[22-23]。风电出力的间歇性和波动性及负荷的时变性导致电力系统节点的注入功率是在一定的范围内变化的，需要采用不确定性分析方法来描述电力系统并对其运行进行优化。而传统的确定性分析方法只是基于某一时间段面或某确定工况，并不是分析不确定性因素的有效手段。在不确定分析方法中，区间算法备受学者关注，利用区间思想来表示问题的不确定性，文献[24-25]以区间量表征风电等可再生能源的功率预测结果，直观反映了可再生能源等不确定因素对微电网经济运行的影响程度；文献[26]通过引入决策变量的区间偏序将区间线性优化问题转化为确定性的多目标问题进行求解，简单易行，但偏序的定义和阈值的选取有较大的主观性。

本文考虑CS-DWPG中分布式风力发电出力侧和负荷侧EV充电负荷的不确定性，提出一种基于区间算法的CS-DWPG优化调度模型及其求解方法。首先将风电功率和站内基础负荷的预测值用区间量表示，建立以充电站负荷波动最小为目标函数与计及净负荷和EV充电等约束的CS-DWPG区间优化调度数学模型。其次，由于优化模型的决策变量与目标函数间呈非线性相关，并不能通过辅助模型[25]求得目标函数的上、下界，因此提出一种求解优化模型的方法，即通过转换目标函数的方法求解所有决策变量和目标函数的上、下界，通过转换后的目标函数简化模型求解步骤，最终得到EV充电功率的区间值。

1 CS-DWPG的区间优化调度模型

CS-DWPG的基本结构如图1所示，对其区间优化调度即是在考虑源-荷侧的不确定性将风电功率和基础负荷以区间值表示，优化计算EV充电功率的区间值。

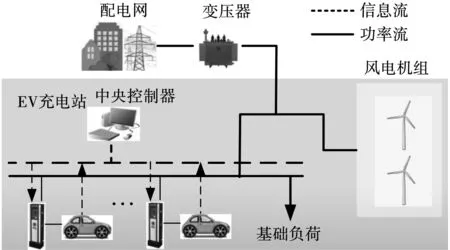
图1 CS-DWPG系统结构Fig.1 Structure of CS-DWPG

1.1 风电功率与基础负荷的描述

由于传统的预测方法并不适用于随机性较大、畸变性较大的序列，因此对风电功率和系统基础负荷的预测采用的是改进灰色马尔科夫预测模型[27]，以提高拟合精确度和预测精确度；同时预测时必然会存在模型误差，所预测出的结果并不能保证完全的准确性，因此采取多场景模拟的方法组成预测区间，以区间形式表示预测结果的不确定性。区间预测流程图如图2所示。

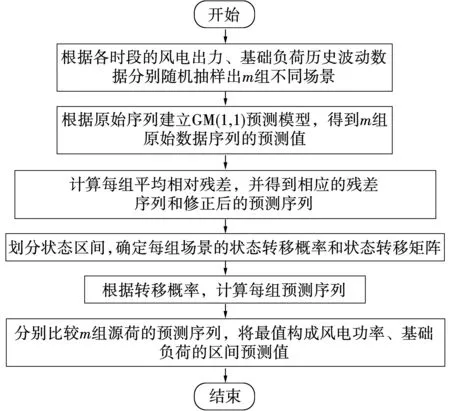
图2 区间预测流程图Fig.2 Interval prediction flow chart

1.2 目标函数

当充电站内源-荷不平衡时，充电站从配电网购电以满足EV充电负荷等需求，为了减少CS-DWPG对配电网运行稳定性的影响，以最小化充电站内负荷波动为目标函数：

(1)

(2)

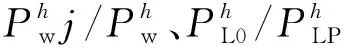
1.3 约束条件

1)基础净负荷约束。

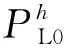
(3)

(4)

(5)

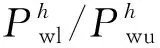
(6)

(7)

(8)

(9)

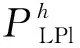
2)EV充电功率约束。

EV的充电功率应保证在可充电的时段内不超过其上限，而在不可充电的时段内，其充电功率应限定为0，即满足：

(10)

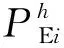
图3 EV可充电时段示意图Fig.3 Schematic diagram of EV charging period

3)充电需求约束。

在Ti2前，EV的充电需求应得到满足即

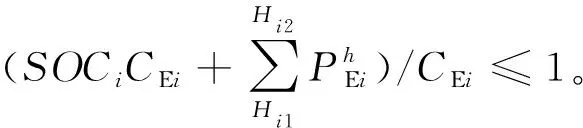
(11)

式中SOCi、SOCie和CEi分别表示第i辆EV在Ti1时的荷电状态、期望荷电状态和动力电池容量。

1.4 区间优化调度模型

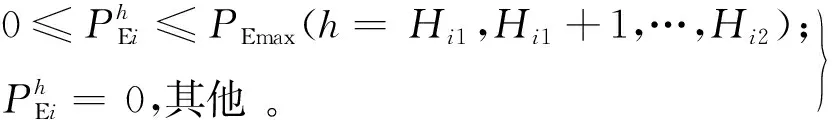
(12)

2 区间优化调度模型的求解方法

由式(12)可见，目标函数与EV的充电功率间无单调性，即EV的充电功率的最值并不对应于负荷波动的最值，因此通过辅助模型直接优化得出的PhEi与目标函数不一定是最优区间。

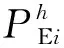
(13)

(14)

根据区间线性优化理论[24,28]，可将模型中的所有区间等式约束转化为确定性约束后，利用线性优化方法进行求解。首先将区间等式约束改写为确定性不等式约束；为了简化计算步骤和方便调用CPLEX优化软件求解，引入权重系数α与β，将式(13)和式(14)的多目标函数分别转换为单目标函数f1和f2，得到两确定性的最值目标函数：

(15)

(16)

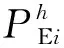
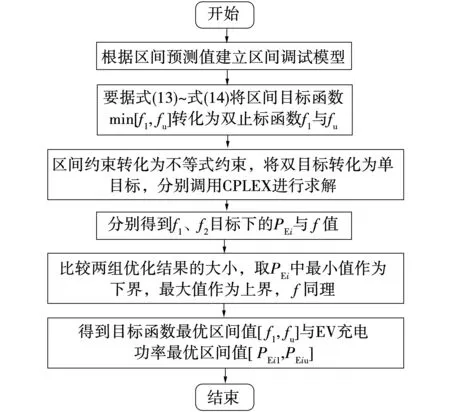
图4 区间线性规划流程图Fig.4 Flow chart of interval linear programming

1)对充电站内的风电功率和系统基础负荷等不确定变量进行区间预测。

2)采用区间值的运算规则把原调度模型转换为区间调度模型，即式(12)。

3)将原区间目标函数转换为两个确定性的双目标函数，即式(13)和式(14)，并将区间等式约束转化为确定性的不等式约束后即式(6)～式(8)，从而得到两个确定性调度模型。

4)根据目标函数的重要程度，引入权重系数把新生成的双目标函数转换为两个单目标函数，即式(15)和式(16)。

5)利用CPLEX分别求解单目标模型，得到EV在各可充电时段内充电功率的上、下限值。

3 算例仿真

设某配电网中一CS-DWPG的风机的数量为2台，在24个调度时段内的风电功率和充电站的基础负荷的区间预测结果如图5(a)和图5(b)所示。假设有10辆EV进行充电，初始荷电状态以及各EV的起始充电时段、最末充电时段如表1所示，各EV的期望荷电状态SOCie=1，车载动力电池的容量CE=50 kW·h，充电功率上限PEmax=20 kW。以参考文献[25]中的区间数据作为灰色马尔科夫预测的历史数据，场景个数m设置为10，最终得到预测结果如图5所示。

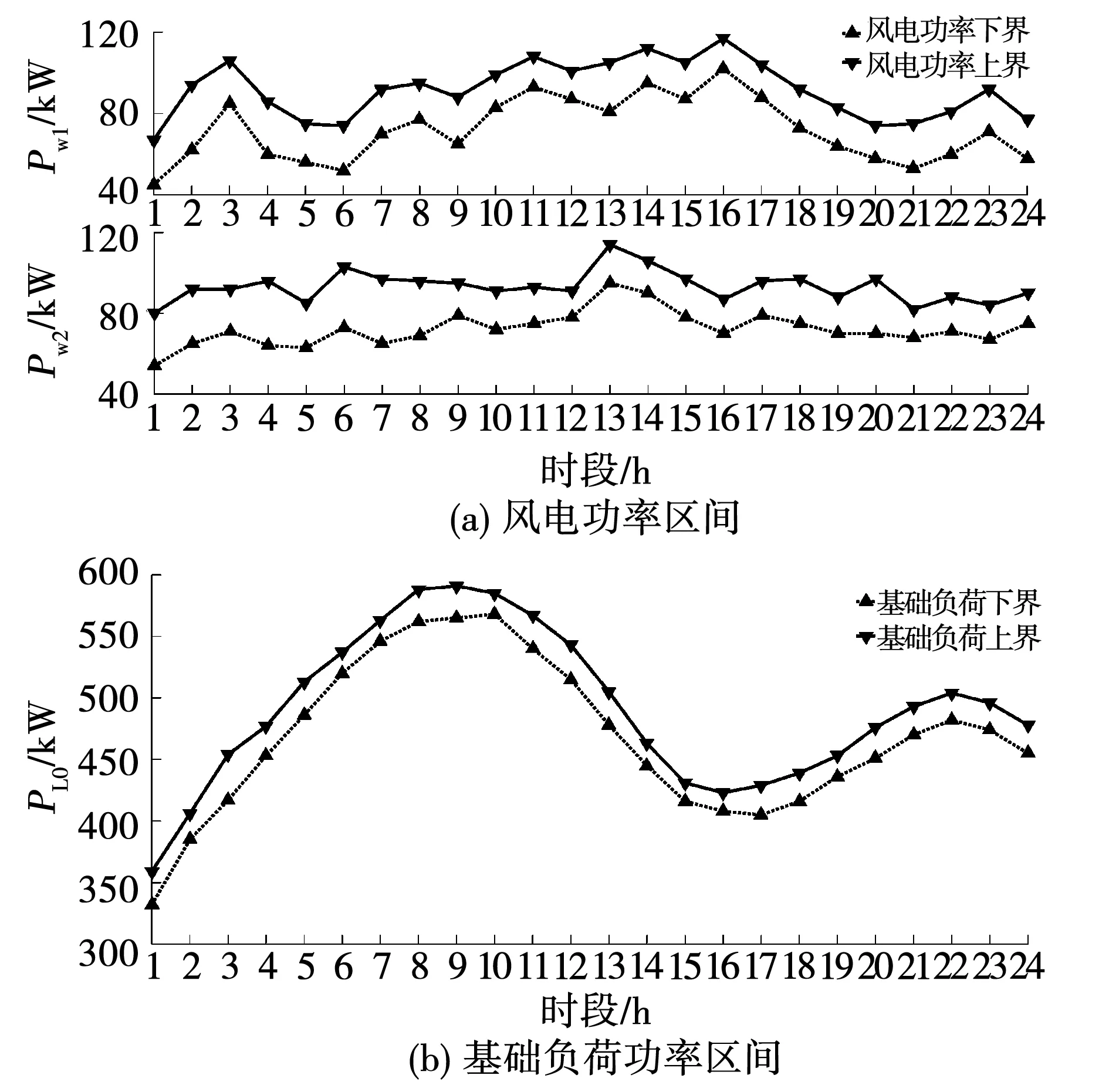
图5 区间功率预测示意图Fig.5 Schematic diagram of interval power prediction

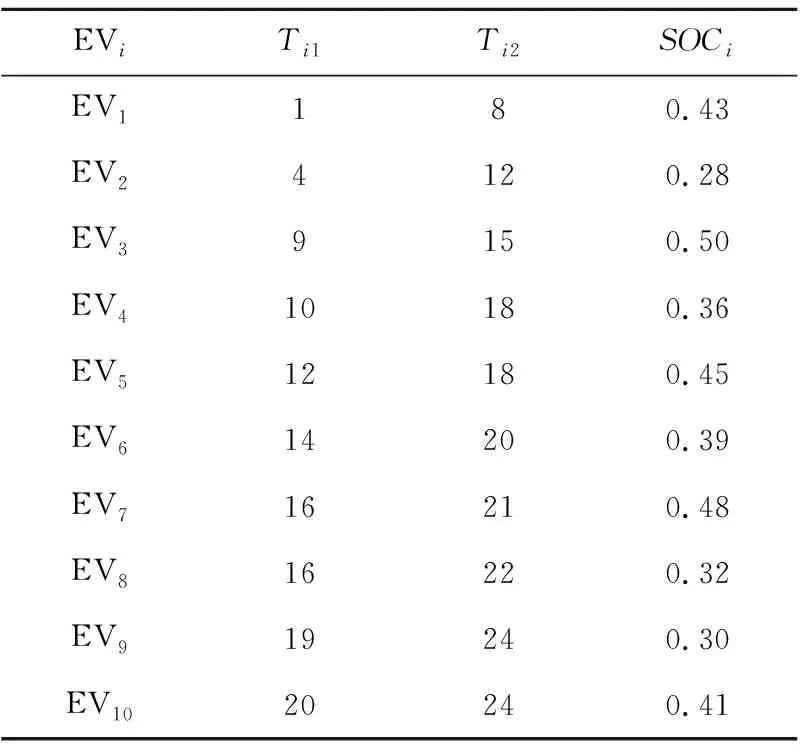
表1 EV的可充电时段及初始荷电状态

3.1 区间调度结果

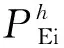
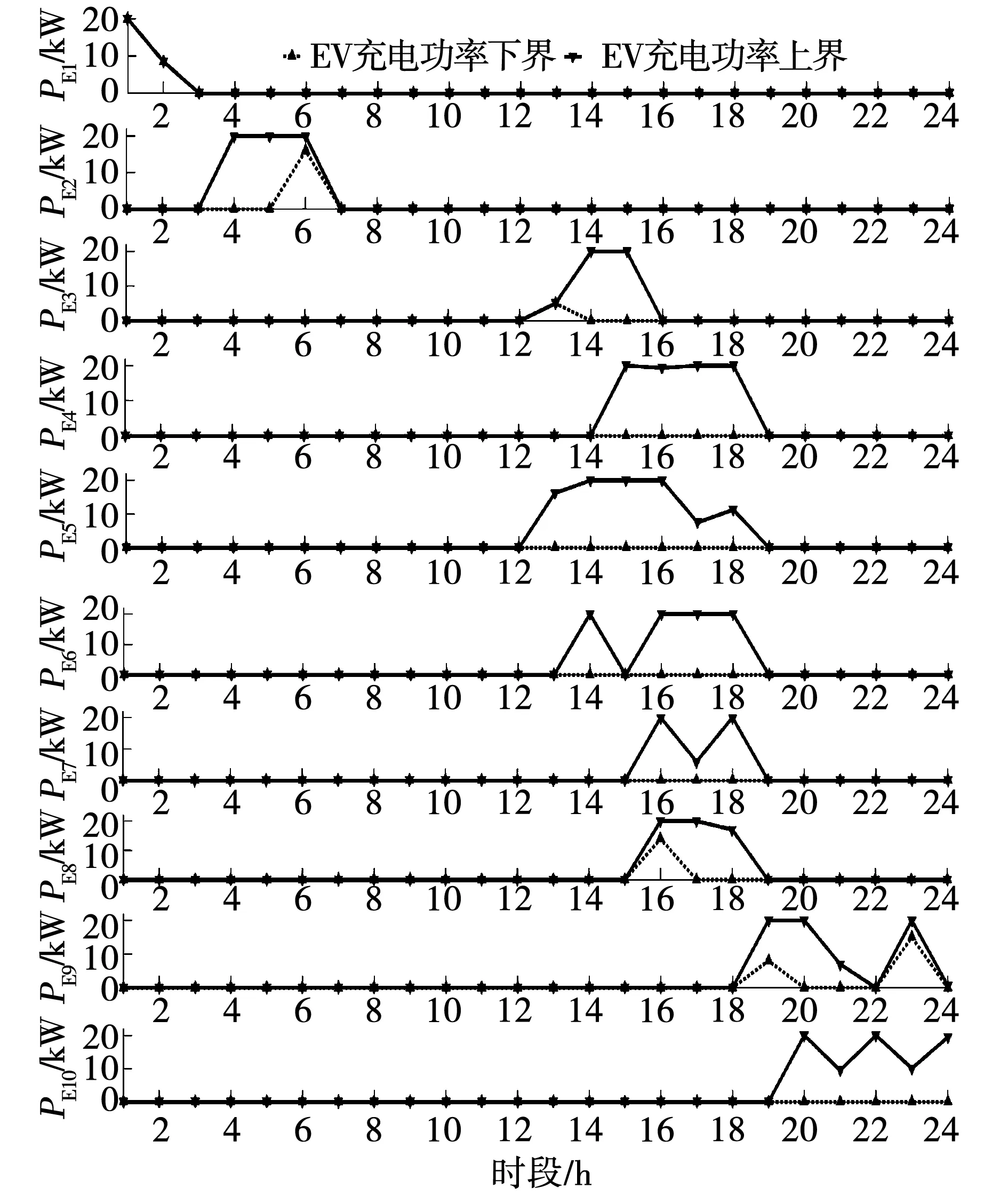
图6 各EV的充电功率区间解Fig.6 Interval solution of charging power for each EV

3.2 基础净负荷的不确定程度对优化结果的影响

为了表明天气变化等不确定性因素对预测偏差的影响，以基础净负荷PLP结果为基准，设置±10%和±20%的波动幅度，对比分析源-荷的不确定程度对CS-DWPG运行的影响，得到的区间调度结果如图8所示。对比图7和图8，可见：当波动幅度为±20%时，14～17时段EV的充电负荷明显减小，几乎无明显的填谷效果；在18和20时段，EV充电负荷陡然增大以致出现了次尖峰。根据图7、图8可得到不同波动范围下调度结果的比较，如表2所示。

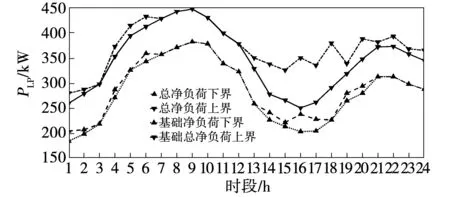
图7 系统基础净负荷与EV充电调度后净负荷Fig.7 System basic payload and EV charging scheduling payload

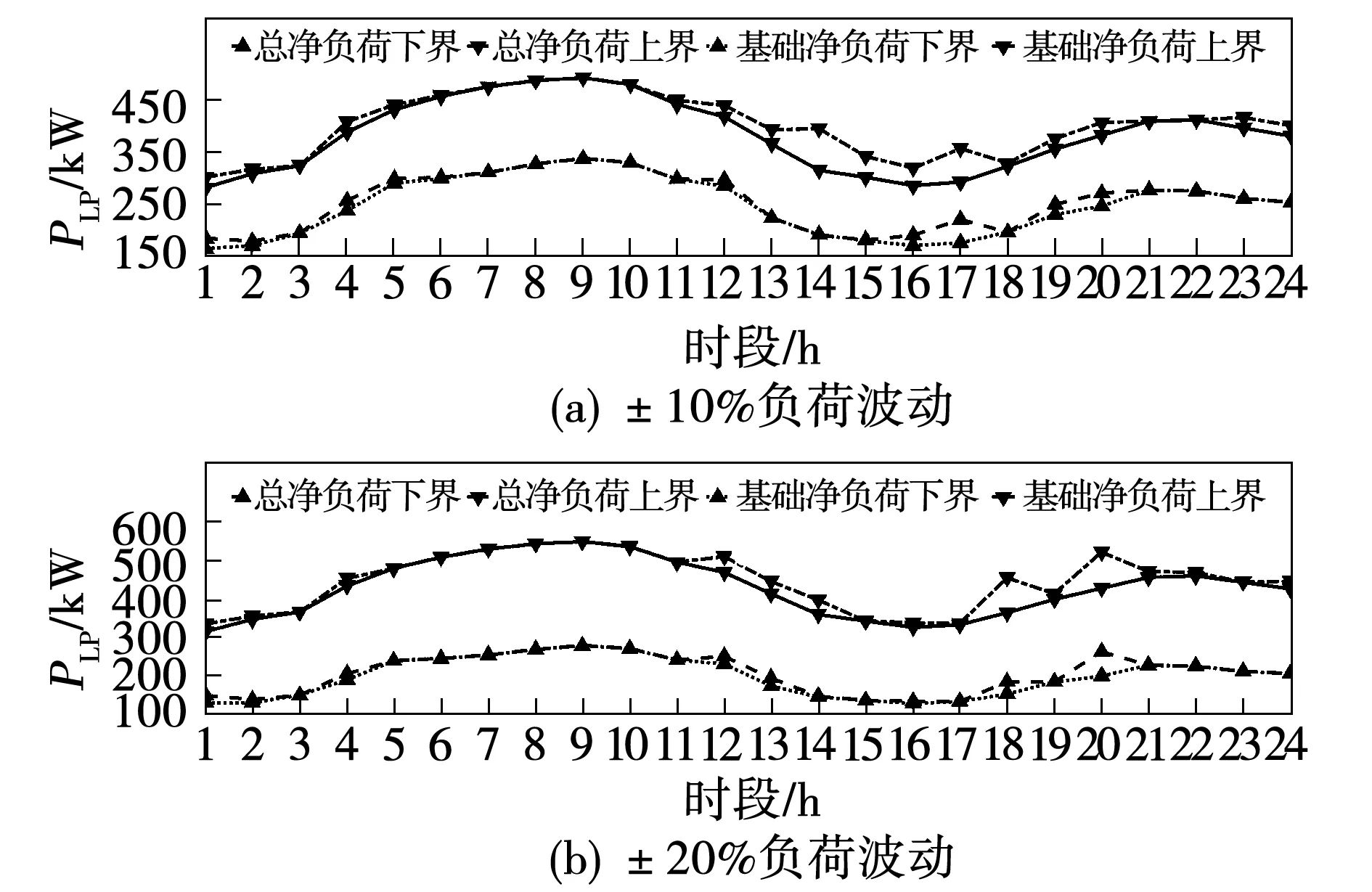
图8 系统基础净负荷与总净负荷调度结果Fig.8 System basic payload and payload

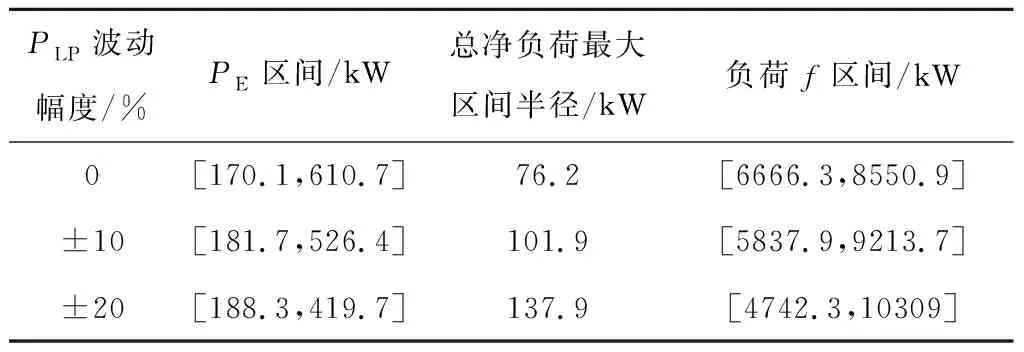
表2 不同波动范围下的调度结果对比

根据表2可看出，随着PLP波动幅度的增大，总净负荷的最大区间半径增大，站内负荷波动区间增大，使充电站运行的波动性变大，运行环境更加恶劣，此外EV可充电负荷区间逐渐减小，使EV充电负荷对站内基础负荷的平抑效果变差。

3.3 与鲁棒优化调度的比较

为突出区间优化方法的优越性，将所提方法与鲁棒优化方法进行对比。由于该区间调度模型可转化为盒型的线性鲁棒优化模型[29]，在3.1小节相同的基础净负荷波动条件下，通过CPLEX求解器对此调度模型进行鲁棒优化求解，最终得到的调度结果如图9所示。

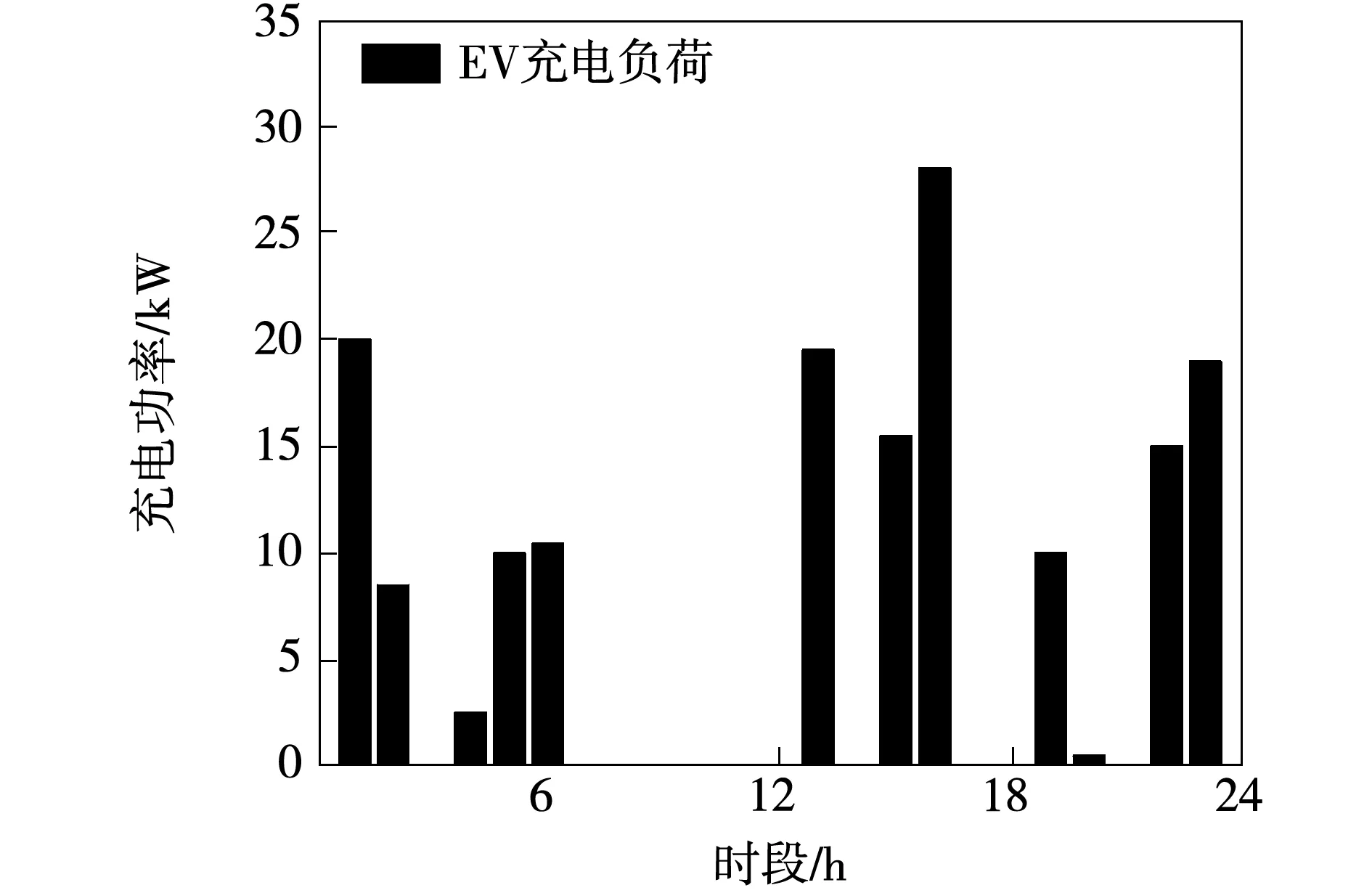
图9 鲁棒优化下的EV充电负荷调度结果Fig.9 EV charging load scheduling by robust optimization

根据图9可知，此时EV充电总负荷为159kW，由于鲁棒优化有较强的保守性，与表2相比，采取的的区间优化策略即使在EV充电总负荷最低的情况下，比鲁棒优化提高了10.1 kW；其次优化结果在鲁棒优化结果填谷最为明显的16时段，EV充电负荷提高了6 kW，说明采用方法的填谷效果更加明显。此外随着基础净负荷的波动范围增大，鲁棒优化的保守性逐渐增大，而区间优化得到的EV充电负荷调度结果最小值有所提高，保守性降低，进一步验证了所提方法在处理不确定性的优越性。

3.4 与确定性点值模型调度的比较

为直观比较区间调度与传统点值调度结果，将3.1小节中已知的区间值分别取其内部的一个点值，组成一个随机的场景，并在该场景下进行优化调度求解。现取两种随机场景,分别如图10、图11所示。

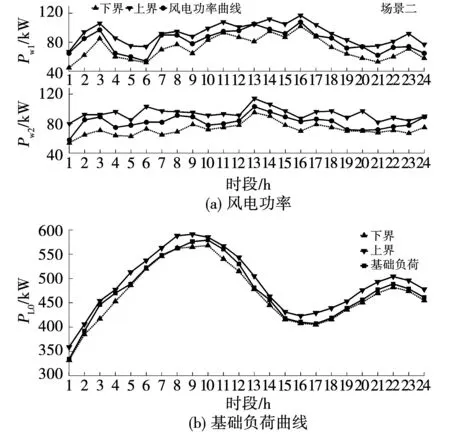
图11 随机场景2下的取值情况示意图Fig.11 Value diagram in random scenario 2

充电站内的风电功率与系统基础负荷在各时段的取值均由场景1与场景2中的点值替代后，通过求解调度模型得到各个EV的充电功率曲线分别如图12和图13所示。

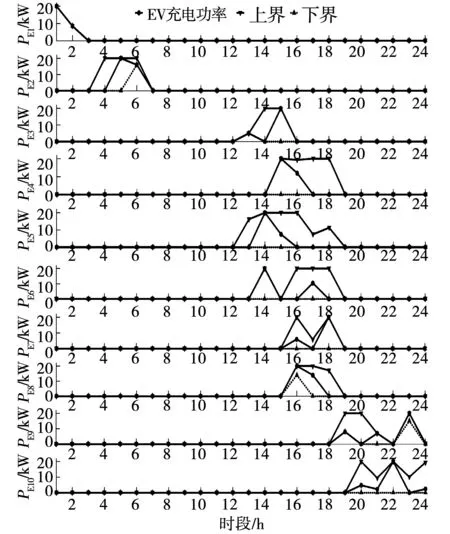
图12 场景1下的各EV的充电功率Fig.12 EV charging power in scenario 1

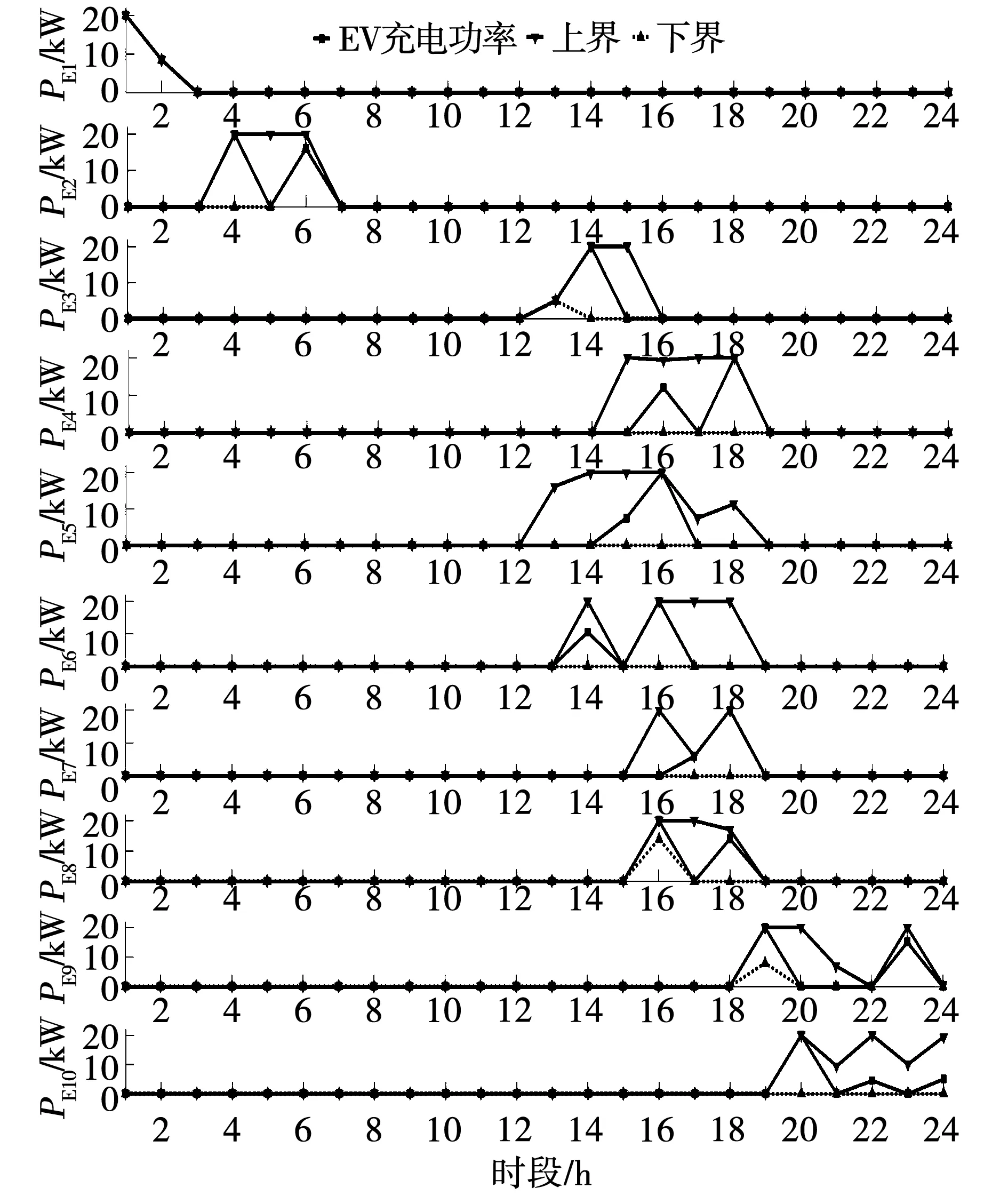
图13 场景2下的各EV的充电功率Fig.13 EV charging power in scenario 2

由图12与图13可见，在两种随机场景下，各EV的充电功率曲线均不超出图6中所示的EV充电功率的区间。此外，对应于场景1和2的系统净负荷曲线的分布如图14中的所示，与图7相比较，两种随机场景下的系统净负荷曲线的分布均不超出净负荷曲线的区间结果，因此两种场景只是区间调度结果的两种特殊运行情况，而负荷区间结果表明了EV充电站所有的运行工况，即充电站负荷波动范围。

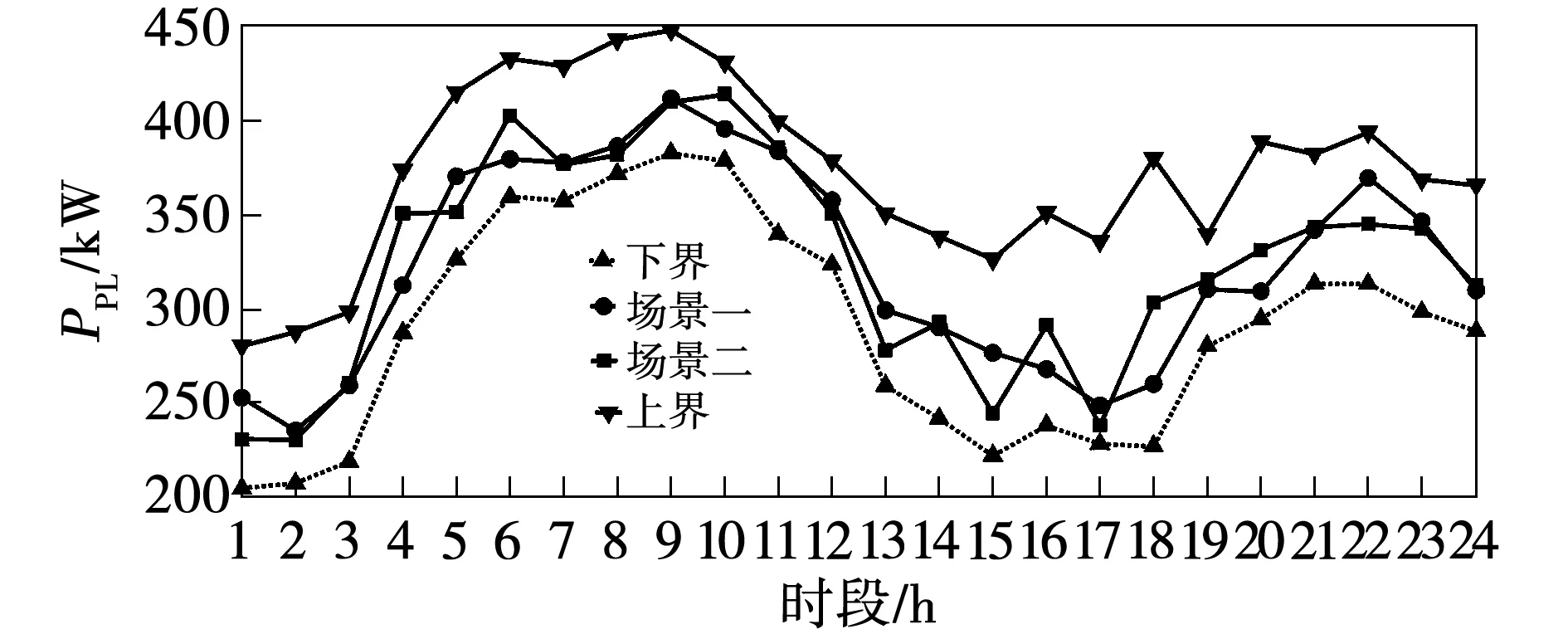
图14 随机场景下的净负荷曲线与其上、下界位置的对比Fig.14 Upper and lower bounds of payload in different scenarios

4 结 论

为解决CS-DPWG源荷双侧功率不确定性对其优化调度的影响，本文提出了含风力发电的充电站区间优化调度方法。通过建模以及仿真结果的比较和分析，可得下面结论：

1)区间法通过上、下界反映了CS-DWPG的“最悲观”的状态，可以考虑风力发电出力和站内基础负荷的所产生的不确定性因素，克服了传统确定性方法以点代面的分析思想。

2)针对提出的区间调度模型，给出了一种计算目标函数与决策变量区间值的方法，方便直接用CPLEX进行求解，避免了目标函数在含有区间绝对值的计算问题。

3)模型考虑了EV充电功率对充电站的影响：随着CS-DPWG源荷的不确定性增大，EV的充电功率区间减小，平抑效果逐渐降低。

4)与鲁棒优化相比，本文方法所得到的调度结果保守性较小，且填谷能力较好。与点值调度相比，区间调度结果完全包含了点值调度结果，能够得到点值调度所没有的信息。

文中所提的目标函数转化方法在求解时具有一定的主观性，其次并未考虑CS-DPWG对配电网的影响，具有一定的局限性，下一步可建立更为详细的主动配电网区间调度模型。