新型双段Halbach阵列轴向永磁联轴器的多目标优化

刘晓，肖罗鹏，崔鹤松，2，黄守道

(1.湖南大学 电气与信息工程学院，长沙 410082；2.机械工业北京电工技术经济研究所，北京 100070)

0 引 言

永磁联轴器[1-2]是传动系统中的一个重要部件。区别于传统的机械接触式联轴器，永磁联轴器利用主、从动转子上的永磁体相对转角实现无接触式传动。永磁联轴器利用静态密封代替传统的动态密封，从根本上解决了工业传动中的泄漏问题，在许多工业场合具有广泛的应用，具有隔离、减震、过载保护和允许对准误差的特性。

永磁联轴器主要结构[1]分成：轴向永磁联轴器和径向永磁联轴器。轴向永磁联轴器[3-4]根据充磁方式不同，分为传统充磁轴向永磁联轴器、Halbach式轴向永磁联轴器(axial magnetic couplings with Halbach array，HAMC)。

与传统的轴向充磁方式相比，理想的Halbach阵列[5-6]建立的磁场波形正弦度大为提高。但在实际生产中，通常采用分段磁块来实现近似的Halbach磁场，分段越多，波形越接近正弦，但结构越复杂[7]。本文将主要研究双段Halbach阵列结构，根据双段Halbach充磁方式不同，分为传统双段HAMC、新型双段[8]HAMC。本文提出的新型双段Halbach阵列结构简单，且气隙磁场波形正弦度高。

作为一种新型的磁力传动装置，转矩与转矩密度是关键指标。在实际设计中，转矩随着永磁体用量增加而增大，但增长速率会下降，造成转矩密度下降。同样，永磁体利用率高能带来高转矩密度，但有时在结构优化后会减小永磁体的用量，造成转矩减小[9]。所以，转矩与转矩密度有时不能同时实现最优，通常需要建立多个目标函数，采用多目标优化方法[10-11]，同时优化两个及以上性能指标。

本文提出一种新型双段HAMC，通过3D有限元法建立新型双段HAMC仿真模型，并且进行参数化分析，研究转矩性能与设计变量的关系。通过仿真得到大量样本点，建立转矩与转矩密度的多项式回归模型。采用非支配排序遗传算法II(NSGA Ⅱ)[12]进行Pareto多目标优化，获得转矩与转矩密度的极大值。最后通过气隙磁密与转矩性能分析，验证新型结构的合理性与优化方法的有效性。

1 双段Halbach阵列分析

轴向永磁联轴器由3部分构成，主动转子、从动转子、气隙。主、从动转子上均安装有永磁体，且极对数和尺寸规格相同，气隙将转子隔开，实现无接触式传动。HAMC的结构示意图如图1所示。

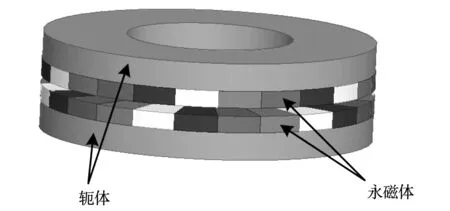
图1 Halbach轴向永磁联轴器Fig.1 Axial magnetic couplings with Halbach array

HAMC转子上的不同充磁角度的永磁体按一定顺序排列，气隙内的磁场强度增大，轭铁处的磁场强度减弱。如图2所示，阵列有磁化角度θ、磁块厚度h、极弧系数α这几个主要参数，图2(a)为传统双段Halbach阵列，磁化角度θ为90deg，图2(b)为新型双段Halbach阵列，磁化角度θ为60deg。

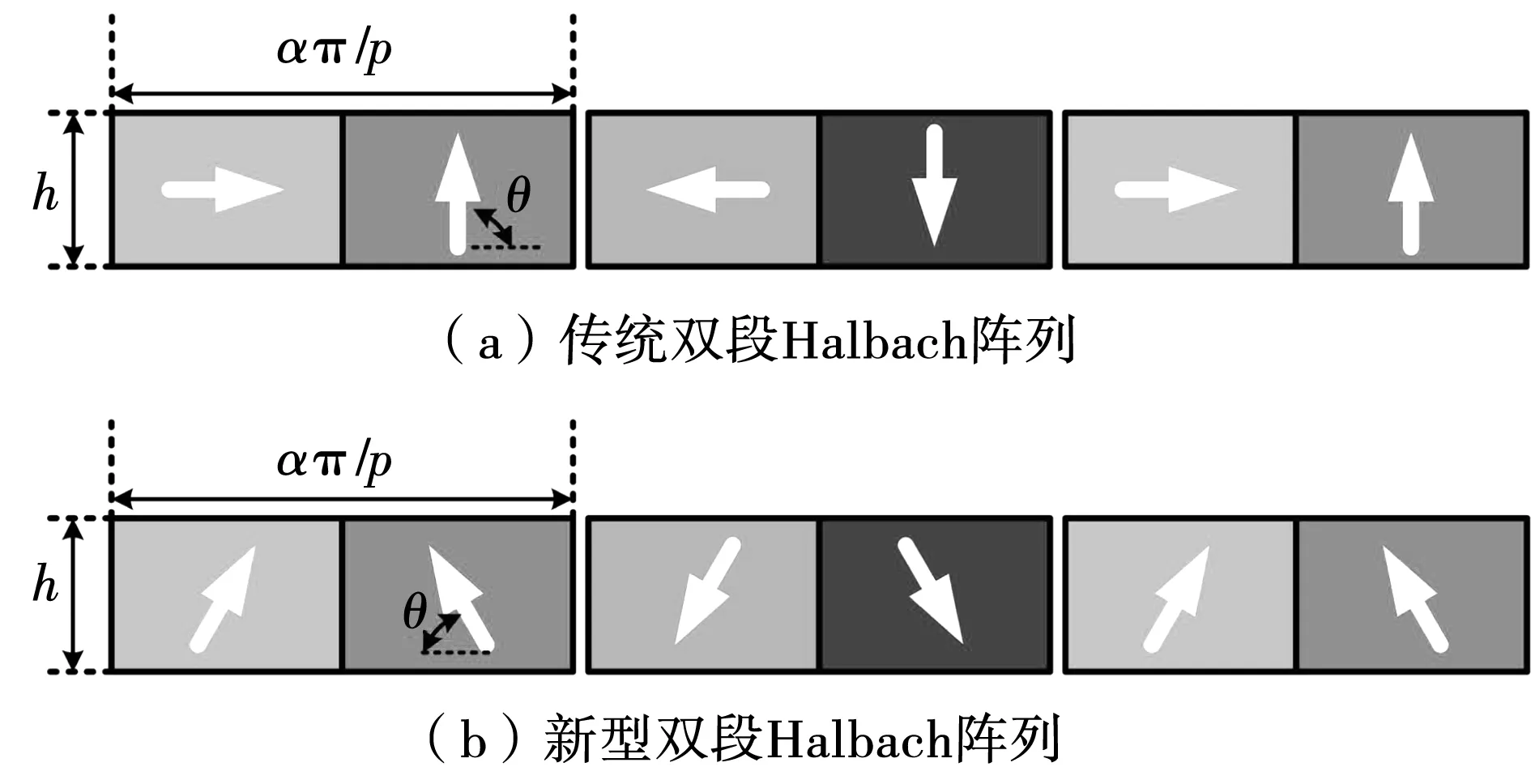
图2 不同充磁方式阵列Fig.2 Different magnetization arrays

由于磁块厚度h、极弧系数α与双段Halbach阵列气隙磁密密切相关[13-14]，所以研究磁化角度θ、磁块厚度h、极弧系数α对HAMC转矩性能的影响，其他未研究的参数保持保留为原始设计。关键设计参数，如表1所示。

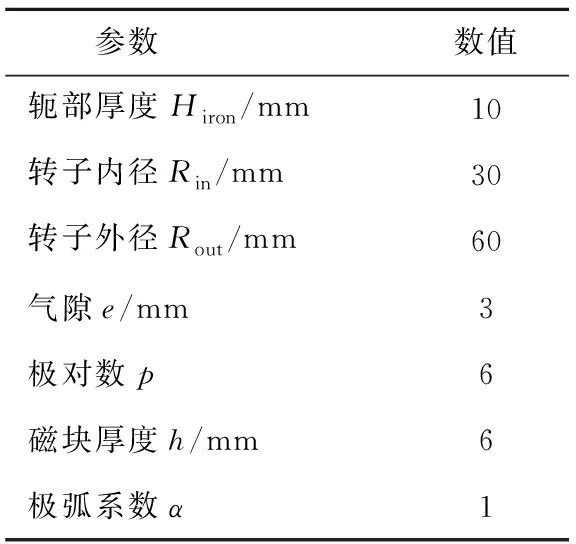
表1 HAMC的关键参数

将从动转子保持不动，同时改变主动转子的机械角度，可以得出传统双段HAMC和新型双段HAMC 的静态转矩如图3所示。可以看出，随着机械角度的变化，主动转子的静态转矩呈正弦变化，且周期为360deg/p=360deg/6=60deg。传统双段HAMC的转矩为60.80 N·m，新型双段HAMC的转矩为69.94 N·m，提高了15.03%。

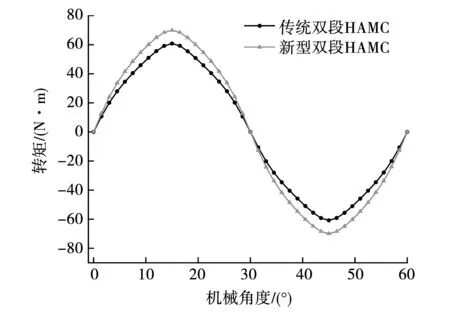
图3 不同HAMC静态转矩Fig.3 Static torque of different HAMC

新型双段HAMC相较于传统双段HAMC，转矩性能得到了提高，既增强了HAMC的转矩性能，又避免了Halbach磁块分段过多而导致结构复杂。在下一部分，将仔细研究磁化角度θ、磁块厚度h、极弧系数α对新型双段HAMC转矩性能的影响。

2 参数分析

由于磁化角度θ、磁块厚度h、极弧系数α与新型阵列气隙磁密密切相关，在本节中，重点研究新型阵列的3个关键参数对新型双段HAMC转矩和转矩密度的影响，有效体积为磁块体积，其他参数保持恒定。

2.1 单参数分析

磁化角度θ对转矩和转矩密度的影响曲线如图4所示。θ变化时，其他参数不变，有效体积不变，所以这两条曲线的变化趋势是相似的。磁化角度θ超过某一角度时，气隙磁密强度减弱，导致转矩性能下降。保持其他参数不变，θ在45deg到75deg范围内变化，转矩密度和转矩在θ=65deg最大。θ超过65deg时，转矩性能开始下降。

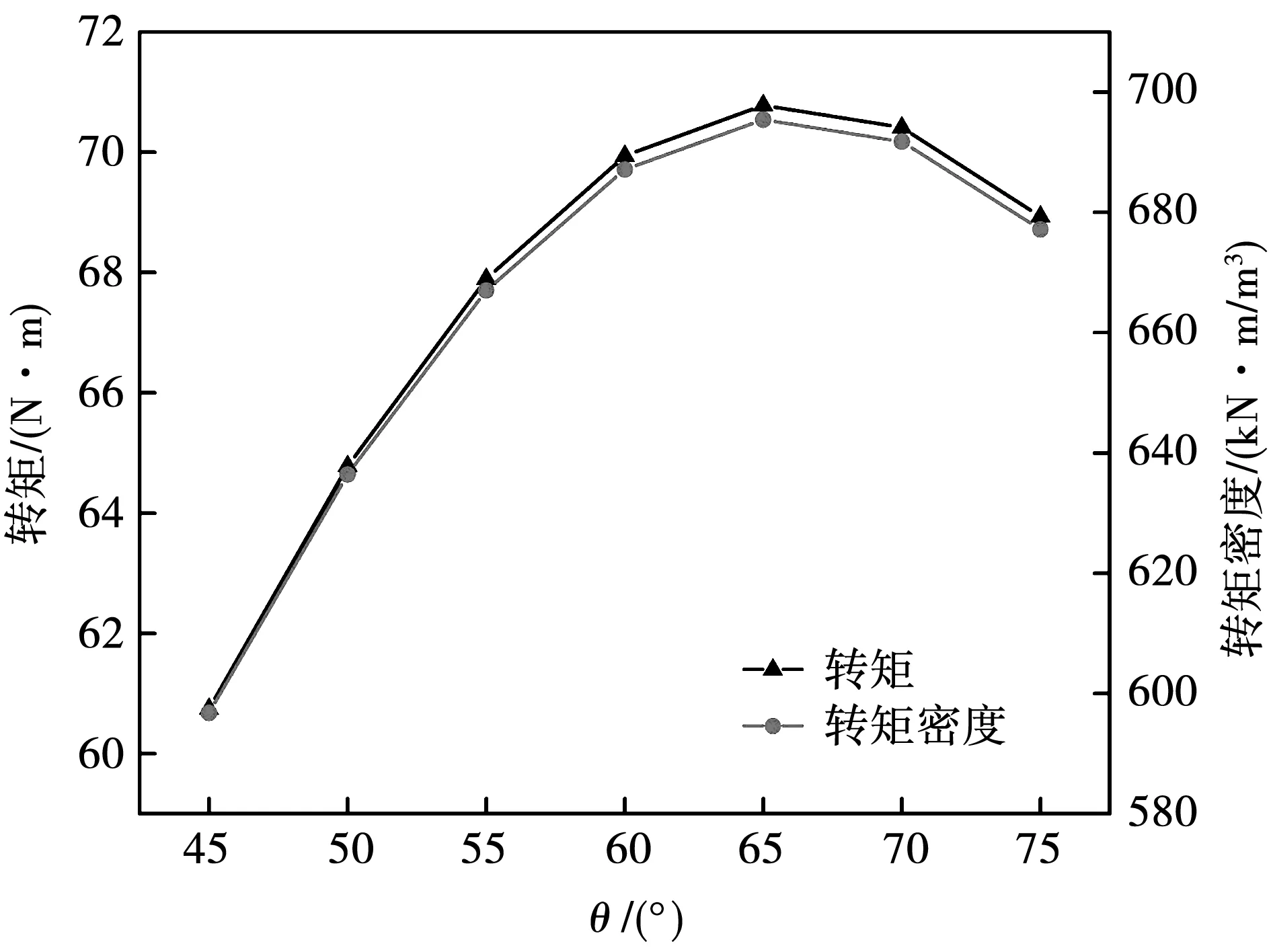
图4 转矩和转矩密度与θ的关系Fig.4 Variation of torque and torque density due to θ

图5展示了磁块厚度h与转矩和转矩密度的影响曲线。随着h增大，转矩也随着增大，但增长速率下降。由此可见，磁块厚度增加并不能一直有助于增大转矩密度。保持其他参数不变，h在4 mm到9 mm范围内变化，转矩密度在h=6 mm时最大。

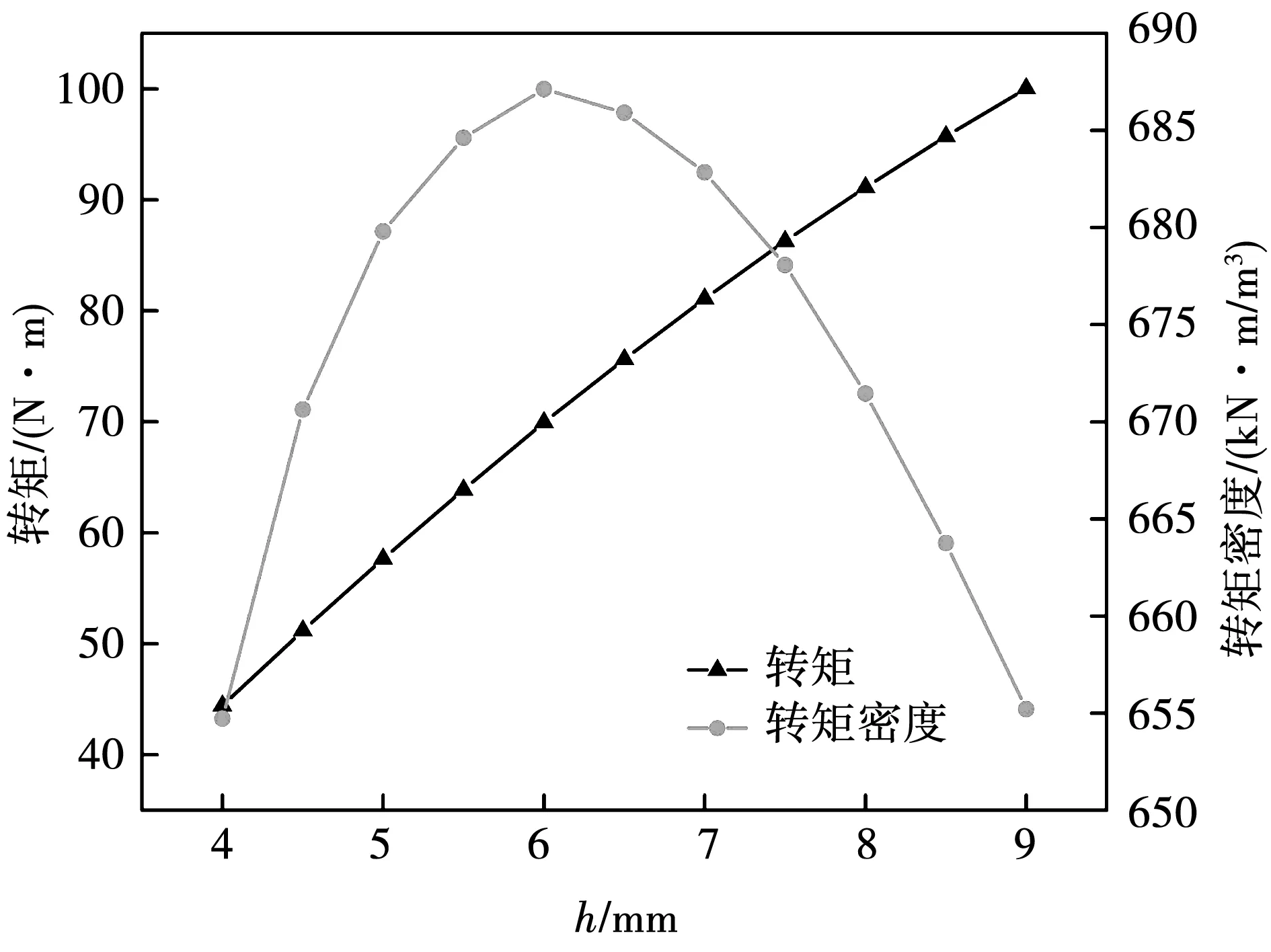
图5 转矩和转矩密度与h的关系Fig.5 Variation of torque and torque density due to h

如图6所示，极弧系数α对转矩和转矩密度的影响关系与h类似。保持其他参数不变，α在0.8到1范围内变化，转矩随着α的增大而增大，但是转矩密度在α=0.9时最大。所以，在新型双段HAMC设计中，转矩和转矩密度之间需要进行调和。

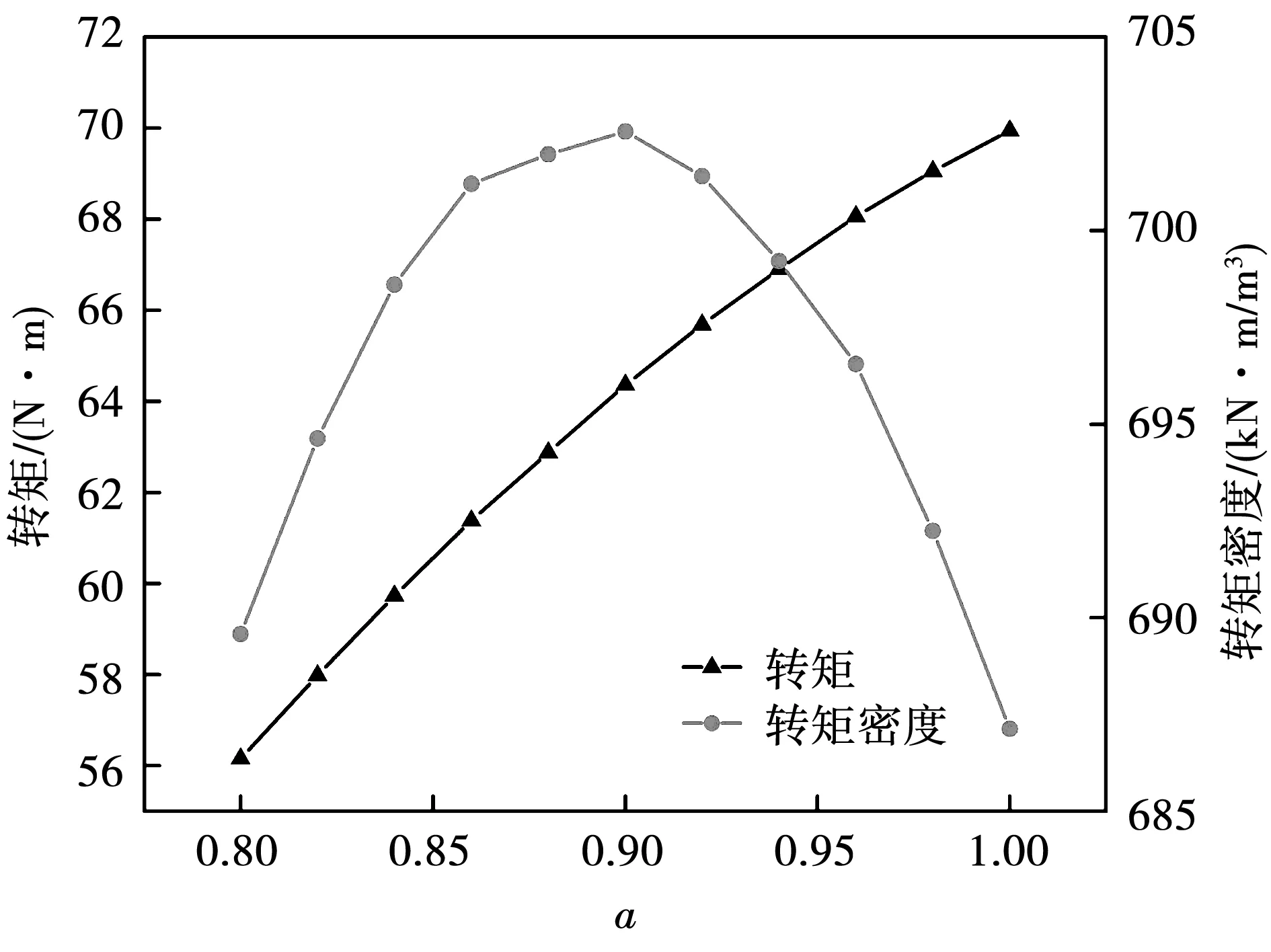
图6 转矩和转矩密度与α的关系Fig.6 Variation of torque and torque density due to α

2.2 多参数分析

图7展示了不同的磁化角度θ和磁块厚度h对转矩和转矩密度的影响。保持其他参数不变，θ变化范围为45deg到75deg，h变化范围为4 mm到9 mm。θ在一定范围内有助于转矩的增大，h的增大有助于转矩的增大，但转矩密度随着θ与h的增大呈现先增大后减小的趋势。保持h=6 mm，且θ从45deg到75deg变化时，转矩从60.74 N·m增长到70.78 N·m，然后降到68.93 N·m。同样，保持θ=60deg，且h从4 mm到9 mm变化时，转矩从44.43 N·m一直增长到100.04 N·m。但是，转矩的增长速率随着h的增长而变慢。从图7(b)可以看出，θ保持恒定时，转矩密度先增大再下降。比如当θ=60deg时，转矩密度从654.75 kN·m/m3上升到687.12 kN·m/m3，然后下降到655.22 kN·m/m3。因为θ变化时，新型双段HAMC有效体积不变，转矩和转矩密度变化趋势一样。但θ取不同值时，最大转矩密度处的h值不同，例如θ=55deg时，h=7 mm，转矩密度最大且为667.69 kN·m/m3；θ=65deg时，h=6 mm，转矩密度最大且为695.37 kN·m/m3。

当磁化角度θ从45deg增长到75deg，且极弧系数α从0.8增大到1时，其他参数不变，其转矩和转矩密度曲线如图8所示。对比图7与图8可知，θ与α对转矩和转矩密度的影响与图7类似。当α=1，θ变化范围为45deg到75deg时，转矩在θ=65deg最大，且为70.78 N·m。同样，当θ=60deg，α从1减小到0.8时，转矩从69.94 N·m一直下降到56.15 N·m。当θ恒定时，α的变化对转矩密度的影响与图7类似，转矩密度由于永磁体的用量骤减，呈先上升后下降的趋势。当θ=60deg，且α=0.9时，转矩密度最大，为702.55 kN·m/m3。从图8(b)可以看出，随着θ的增大，最大转矩密度处的α值不同，例如θ=60deg时，α=0.9，转矩密度最大且为702.55 kN·m/m3；θ=70deg时，α=0.8，转矩密度最大且为739.53 kN·m/m3。磁化角度θ和极弧系数α共同影响着转矩和转矩密度。

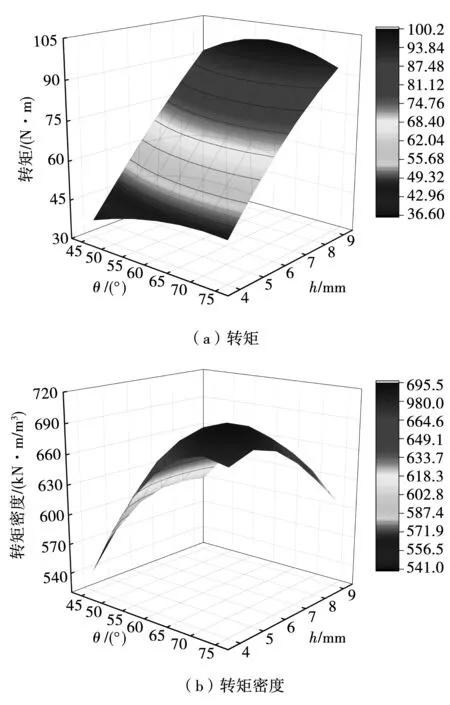
图7 转矩性能随θ和h变化规律Fig.7 Variation of torque performance due to θ and h

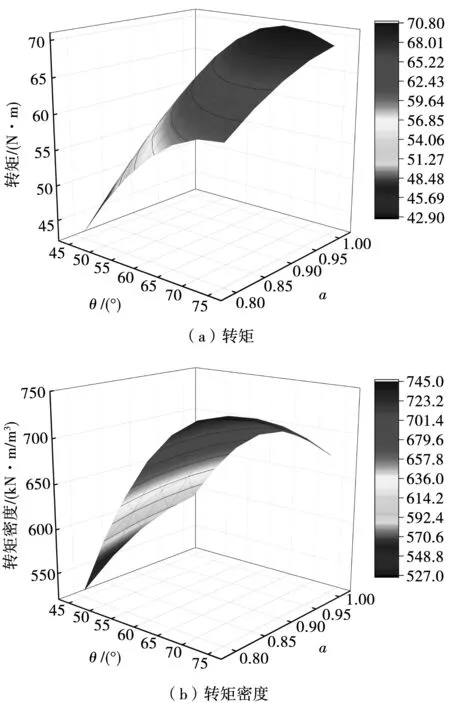
图8 转矩性能随θ和α变化规律Fig.8 Variation of torque performance due to θ and α

图9展示了不同的磁块厚度h和极弧系数α对转矩和转矩密度的影响。保持其他参数恒定，h从4 mm增长到9 mm，α从0.8增长到1。h与α的增大有助于转矩的增大，但α使转矩的增长速率要小于h，那么h的影响更大。保持h=6 mm，α的变化范围为0.8到1，转矩由56.15 N·m增长到69.94 N·m。同样保持α为1时，h从4 mm增长到9 mm，转矩由44.43 N·m变化到100.04 N·m。但是，转矩会随着h和α的增大而增长速率变缓。结果如图9(b)所示，转矩密度随着h和α的增大，先上升后下降。例如，h=6 mm时，转矩密度由689.55 kN·m/m3增大到702.55 kN·m/m3，然后下降到687.12 kN·m/m3。保持α为1，转矩密度由654.75 kN·m/m3增大到687.12 kN·m/m3，然后下降到655.22 kN·m/m3。

图9 转矩性能随h和α变化规律Fig.9 Variation of torque performance due to h and α

3 多目标优化与分析

3.1 拟合模型

通常，如果优化目标与优化变量之间没有已知的函数关系，那么可以通过拟合函数[15]来代替。拟合模型既可以实现较高的精确度，又可以取代耗时的有限元模型，加快优化进度。

根据3D有限元分析结果，得出大量采样点，利用多项式回归模型拟合目标函数转矩(Te)和转矩密度(Td)，并使用θ、h、α这3个优化变量，目标函数表示为：

Te=-333.112+5.197θ+5.642h+

337.626α-0.024θ2-0.545h2-

133.492α2-0.026θh-1.889θα+

13.885hα,

(1)

Td=-2903.541+57.454θ+68.592h+

3411.056α-0.226θ2-4.533h2-

1286.678α2-0.849θh-22.572θα+

40.316hα。

(2)

为了评估拟合函数的准确性，采用平方值(R2)，F检验统计量(F-statistic)和F-statistic的概率p。准确性评估见表2，两个目标函数的R2接近1，且F-statistic很大，p小于0.05，可以判断拟合结果的准确性很高。

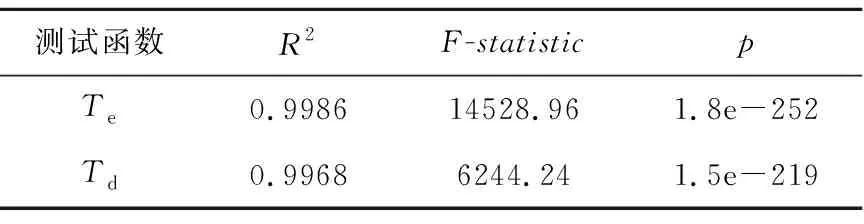
表2 拟合模型的准确性评估

3.2 优化模型

尽管参数变化对转矩和转矩密度的影响在前面部分已经研究了，但是各个参数之间相互影响，依然无法得出全局最优解。新型双段HAMC的多目标优化是解决Pareto解集的问题，具有一系列非劣解。在新型双段HAMC的多目标优化问题中，目标函数是转矩(Te)和转矩密度(Td)。取θ=60deg、h=6mm、α=1为初始设计参数，引入转矩参考值(Teref)和转矩密度参考值(Tdref)，使得两个目标函数有比较性。

其他参数保持原始数据，优化函数的公式可以写成

(3)

约束条件如下：

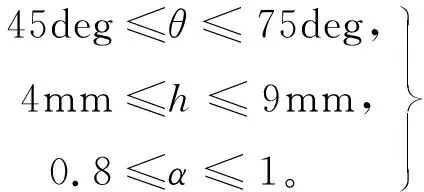
(4)

采取NSGA Ⅱ对新型双段HAMC进行多目标优化，与传统的单目标优化不同，NSGA Ⅱ可以搜索全面的Pareto解决方案，更好地实现转矩和转矩密度的极大化。

Pareto前沿展示了非劣等解集，如图10所示。从图10可以看出，转矩与转矩密度不能同时达到最优。经过3D有限元法验证，若只考虑转矩，最大值达99.97 N·m；反之，只考虑转矩密度，则最大值达758.01 kN·m/m3。

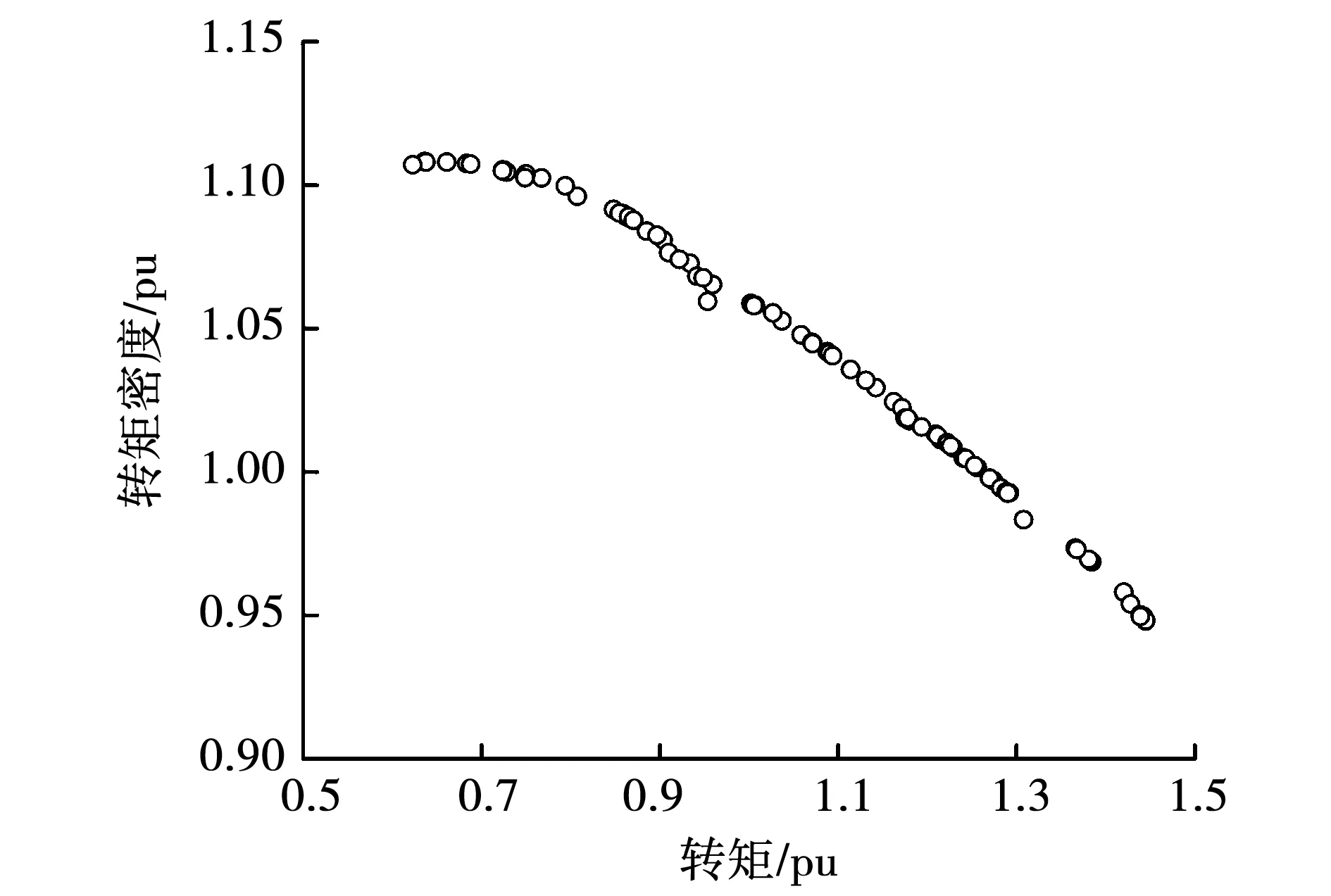
图10 多目标优化的Pareto前沿Fig.10 Pareto frontier for multi-objective optimization

但在实际生产中，需要同时保证转矩和转矩密度都较大，如表3所示，选取了θ=69.52deg、h=6.99 mm、α=0.87为设计优化参数。将这组优化数据代入3D有限元仿真模型，比较结果见表4，可见拟合结果与有限元模型误差在2%以内。

表3 设计优化参数

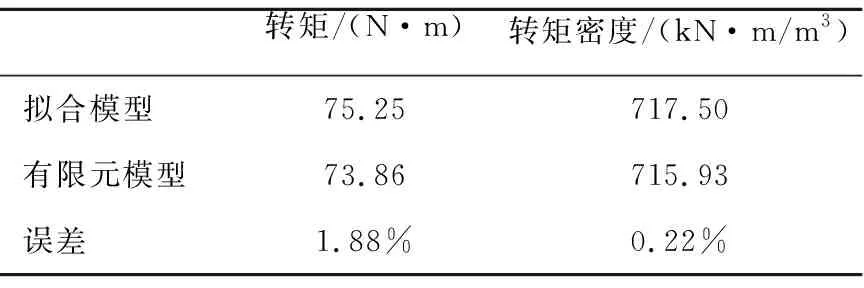
表4 优化模型误差

新型双段HAMC优化前后的稳态输出转矩如图11所示，经过NSGA Ⅱ优化，优化前转矩为69.94 N·m，优化后为73.86 N·m，提高了5.60%。且由表5可知，转矩密度提高4.19%，达到了715.93 kN·m/m3。

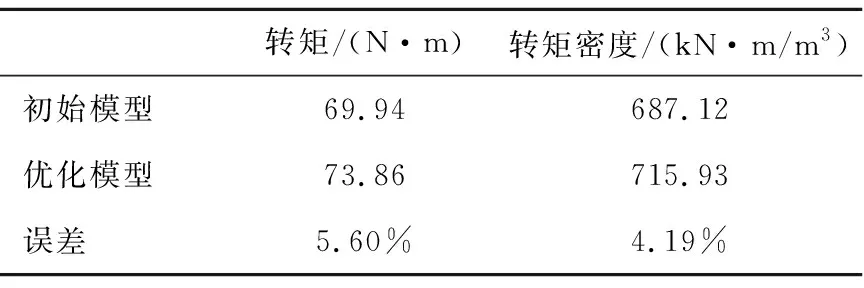
表5 优化前后转矩性能

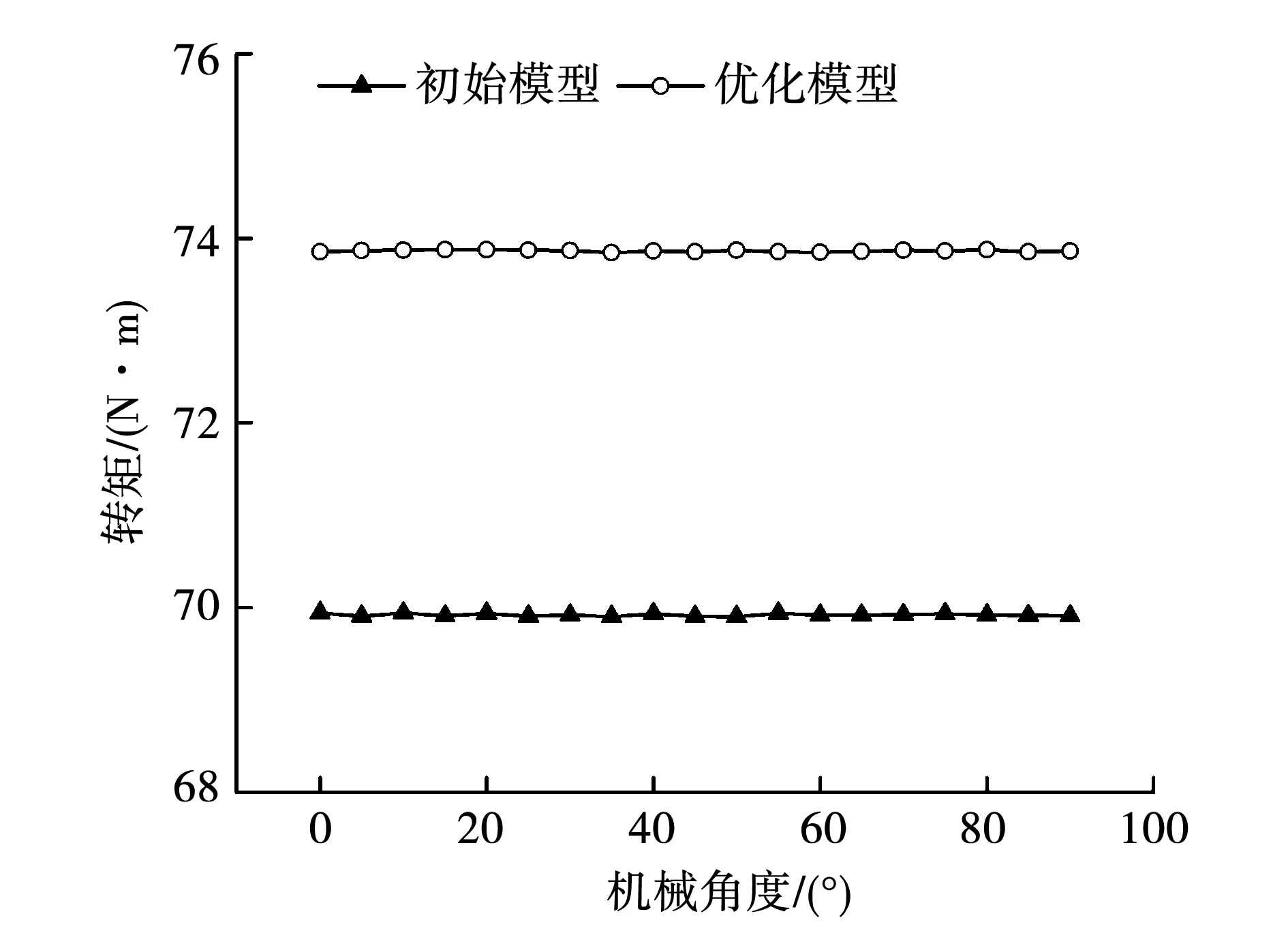
图11 优化前后稳态输出转矩Fig.11 Steady output torqueof non-optimized and optimized HAMC

3.3 气隙磁密和转矩性能分析

图12展现了新型双段HAMC优化前后两个模型在平均半径处气隙磁密的FFT分解。为了深入分析优化后的新型双段HAMC模型，利用Maxwell应力张量来计算转矩[3]，得出平均半径处的转矩为

(5)

则平均半径处气隙磁密的轴向分量Bz(θ,z)和切向分量Bθ(θ,z)表达式分别为：

(6)

(7)

将式(6)与式(7)代入式(5)中，则式(5)可转换为

(8)

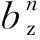
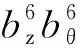
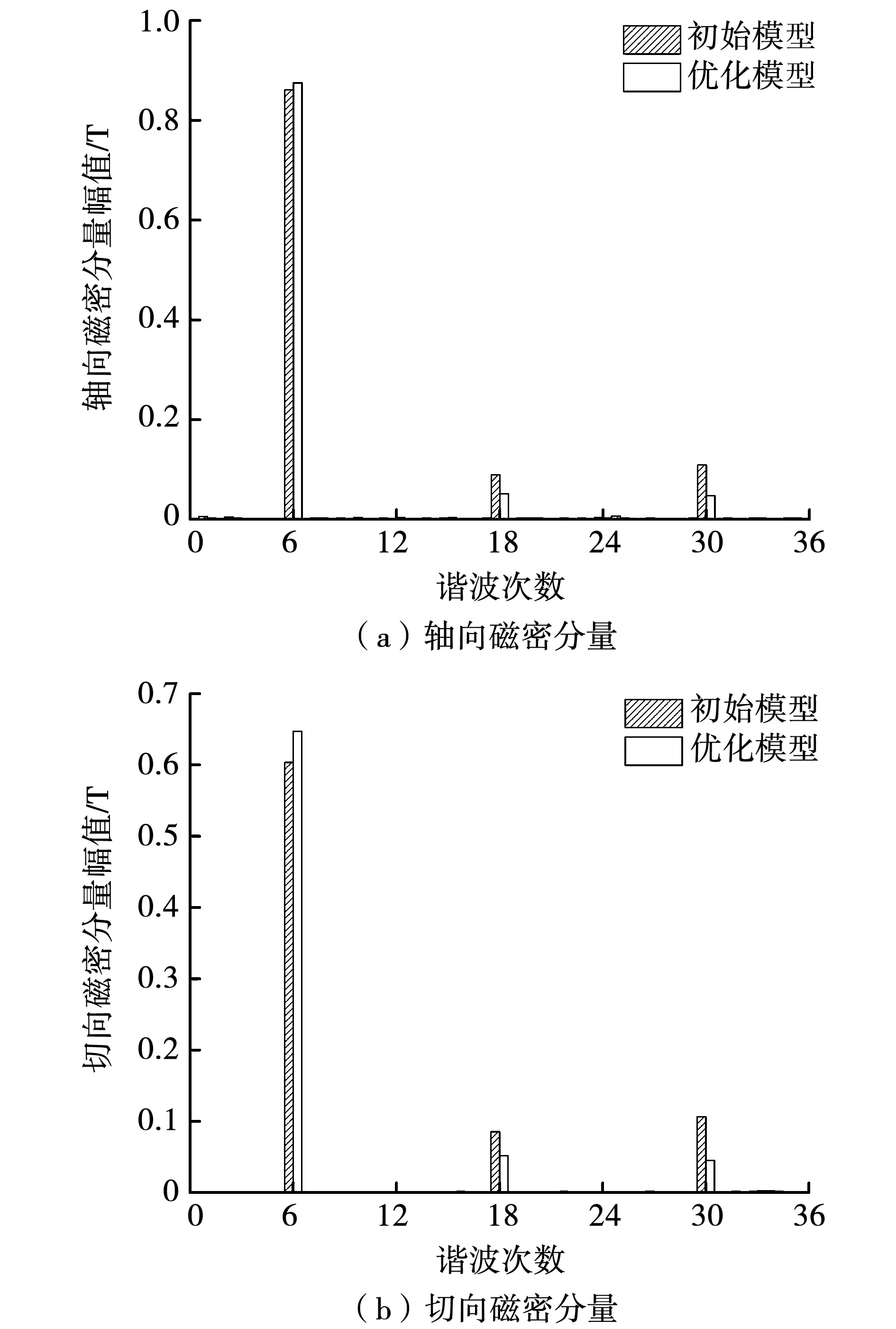
图12 平均半径处气隙磁密FFT分解Fig.12 FFT decomposition of air gap magnetic density at average radius

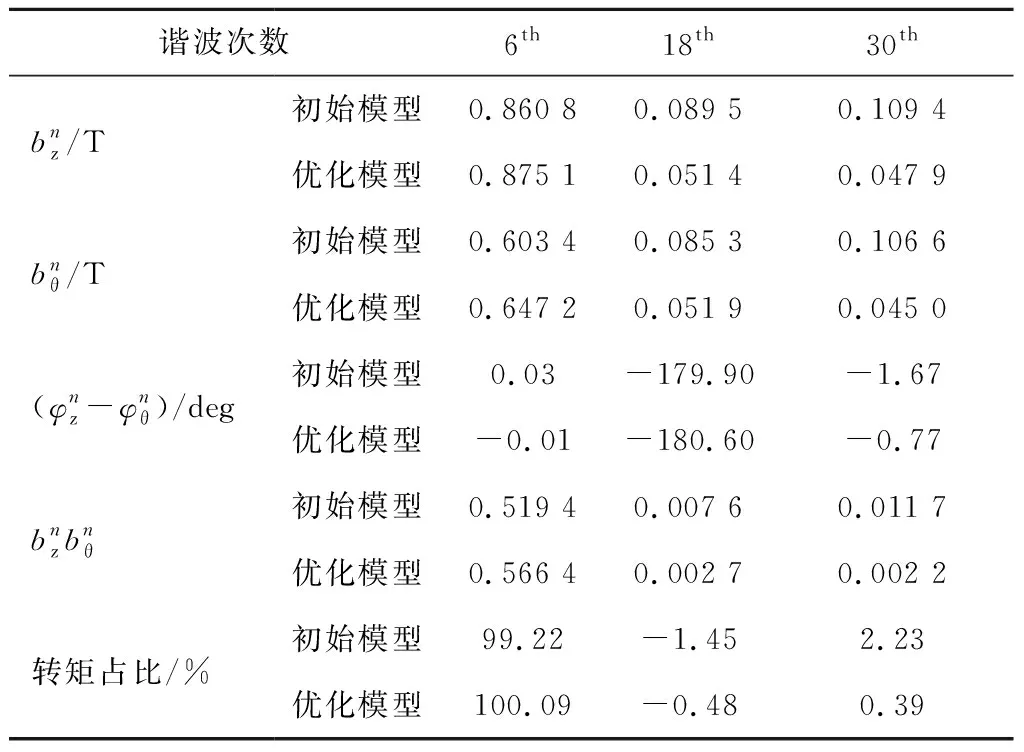
表6 平均半径处气隙磁密分布

设计变量参数不但会影响气隙磁密基波幅值(6次谐波分量)，而且会影响气隙磁密正弦性[13]。为了详细研究气隙磁密对转矩性能的影响，引入气隙正弦性畸变率KB来衡量气隙磁密的正弦性，可以表示为

(9)

其中：Bm1为气隙磁密基波幅值；Bm2，Bm3…Bmk为各次谐波幅值。由于转子极对数为6，气隙磁密周期数为6，气隙产生6对极波，即Bm1=b6，Bm2=b12…Bmk=bk6。

为了深入分析单个设计变量对气隙磁密和转矩性能的影响，将初始参数定义为初始模型，h保持不变，θ和α优化之后的模型定义为改进模型(θ和α改变，h不变)，NSGA Ⅱ优化之后的模型定义为优化模型(θ、h和α均改变)。根据式(9)，表7列出了新型双段HAMC不同设计参数与气隙磁密值。

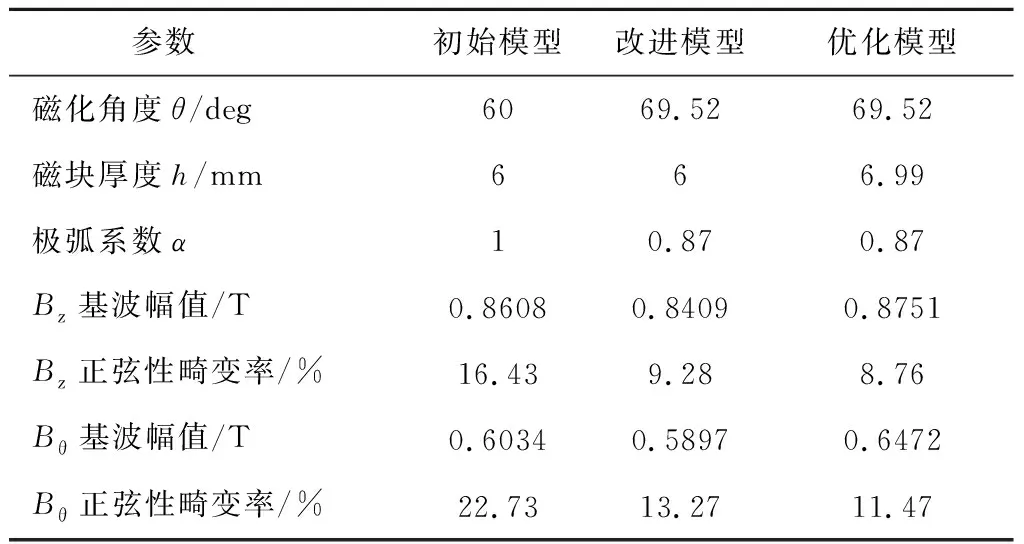
表7 不同参数的新型双段HAMC

初始模型与改进模型对比如图13所示，Bz正弦性畸变率由16.43%下降到9.28%，Bθ正弦性畸变率由22.73%下降到13.27%，θ和α的优化显著提升了气隙磁场的正弦性，但基波幅值也略有下降。所以可以通过增大磁块厚度h，提升基波幅值，弥补转矩的下降。与初始模型相比，优化模型的Bz正弦性畸变率下降到8.76%，Bθ正弦性畸变率下降到11.47%，Bz基波幅值上升到0.875 1T，Bθ基波幅值上升到0.647 2T，既降低了气隙磁密正弦性畸变率，又提升了基波幅值。Pareto多目标优化之后的新型双段HAMC转矩性能整体得到了提升，与3D有限元仿真结果吻合。

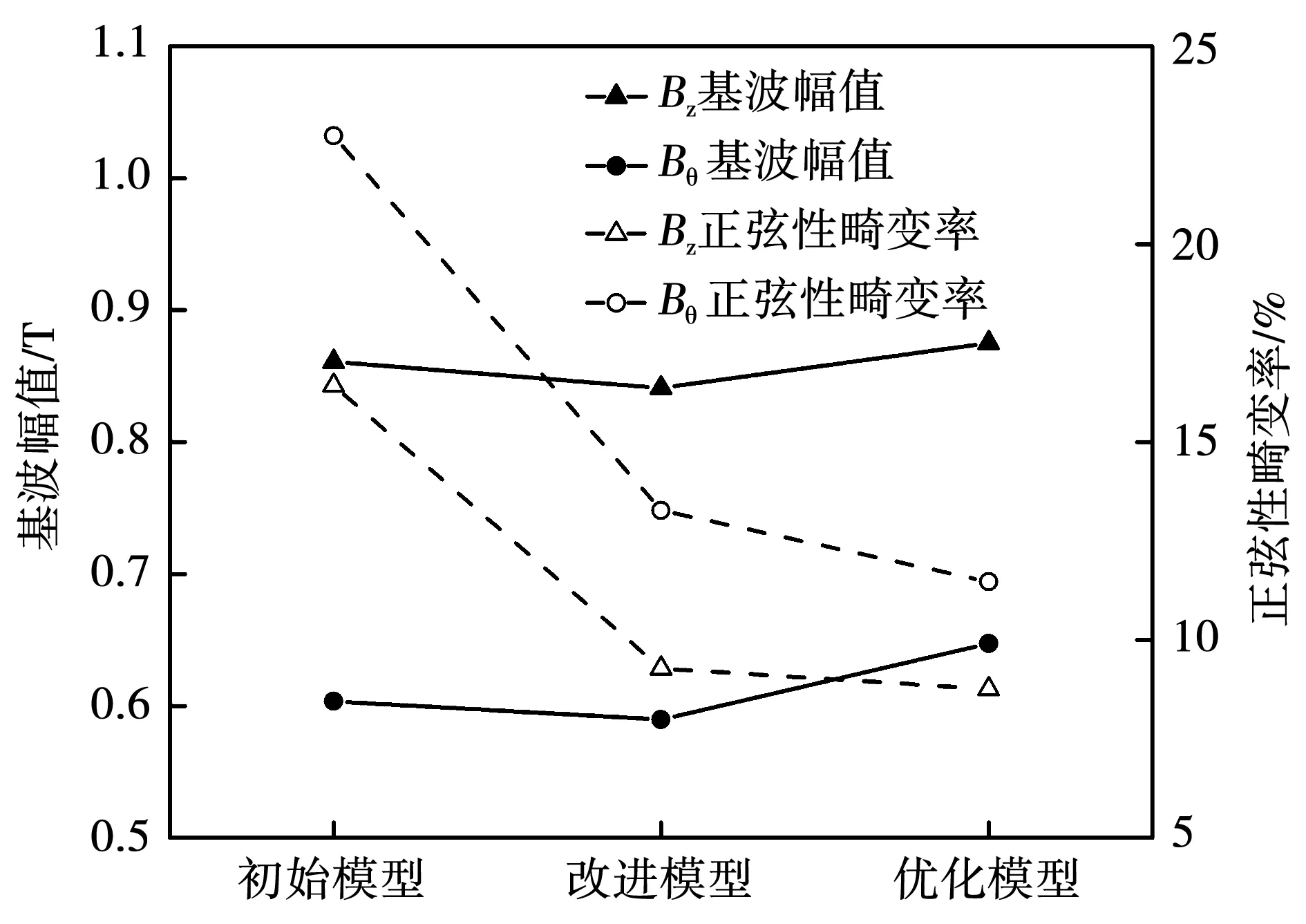
图13 气隙磁密对比Fig.13 Comparison of air gap magnetic density

4 结 论

本文提出了一种新型双段HAMC，并利用多目标优化方法提升转矩性能。横向对比传统双段HAMC与新型双段HAMC的转矩性能，发现新型双段Halbach阵列可以有效地改善转矩性能。以磁化角度θ、磁块厚度h、极弧系数α为关键设计变量，纵向对比各关键设计变量对转矩和转矩密度的影响。为满足实际设计需要，采用NSGAⅡ方法对转矩和转矩密度进行多目标优化，转矩较之前增大5.60%，达到了73.86 N·m，转矩密度为715.93 kN·m/m3，提升了4.19%。气隙磁密和转矩性能分析表明，磁化角度θ和极弧系数α有效改善了气隙磁密正弦度，但基波幅值略有下降，可以调整磁块厚度h弥补转矩，整体提升新型双段HAMC的转矩性能。通过有限元结果验证与分析，进一步证明了新型结构的合理性和多目标优化方法的有效性。