电励磁分块转子磁通切换发电机电磁特性分析

史立伟，严兵，张文超，安俊豪，丁富康，卞玉康

(山东理工大学 交通与车辆工程学院,山东 淄博255049)

0 引 言

磁通切换电机是结合感应电机和磁阻电机的工作原理发展而来的新型无刷电机，在转子上没有线圈或永磁体，通过改变绕制在定子槽内的励磁绕组电流来实现励磁控制，具备故障时灭磁能力，并且结构简单,转矩和功率密度高[1]。电机采用定转子分块结构可以缩短工作磁路，降低电机铁损，磁路的隔离还能提高电机的容错性和可靠性，并且由于分块转子没有凸起，能够在高速运行时降低风阻和噪声[2-3]。结合了两者优点的分块转子磁通切换电机在电动汽车、航空航天、风力发电等对可靠性要求较高的领域有着良好的应用前景[4-6]。

英国纽卡斯尔大学B. C. Mecrow教授最先提出了分块转子磁通切换电机(segmental-rotor flux switching motor, SR-FSM)，并以12/8极样机为例，对该种电机的原理展开了深入研究且进行了大量实验验证，研究结果表明该种电机由于其磁链和反电动势波形都近乎是正弦分布,特别适合于无刷交流运行的应用场合，并且其转矩密度与开关磁阻电机相近[7-8]。针对电机转矩脉动大的问题，通过在分块转子上开槽的方法来达到改变气隙磁导率和气隙磁密各次谐波傅里叶系数的目的，并建立了电机的d-q轴电感分析模型[9-10]。国内学者对分块转子磁通切换发电机(segmental-rotor flux switching generator, SR-FSG)的电磁特性做了大量有限元分析，发现由于定子铁心两条磁路气隙磁阻的差异，在励磁磁动势大于一定值后，磁通会随着励磁磁动势的增加而减小，但是整体来看电机具有较高的功率密度[11-12]。并且现有研究表明奇数极分块转子结构电机不含有偶数次谐波，而偶数极分块转子结构电机无抵消偶数次谐波的特性，从而导致磁链和感应电动势的正负半周期波形不对称[13-15]。由于该原因，现有的分块转子磁通切换电机多采用12/7极或加入复杂的控制电路来提高发电的可靠性[16-17]，这将会大大增加电机的制造成本。

本文首先分析分块转子磁通切换电机的运行原理，并通过有限元法对比奇数极和偶数极分块转子电磁特性的不同。根据转子不同位置综合磁导的不同导致定转子磁势变化的原理，建立电机结构数学模型，通过切向气隙磁障的添加，导致交轴磁阻的增大，以及磁通路径的限制，大大降低偶数次谐波的幅值，从而达到本文所要实现的使感应电动势正负对称的目的，并通过有限元得到新型分块转子磁通切换电机的静态特性与动态特性数据。最后，制造实验样机，实验测试样机的电动势，与仿真结果进行对比，验证本文设计谐波削弱方法的可行性和理论分析的正确性。

1 电机基本结构与工作原理

电励磁分块转子磁通切换发电机(electrical excitation segmental rotor flux-switching generator, ESFSG)的定子上分别绕有励磁绕组和电枢绕组，相邻的励磁绕组绕制方向相反，分块转子嵌入在不导磁的铝制转子套中，如图1所示。电机工作时，励磁绕组通入直流电流产生磁场，通过转子旋转使得在电枢绕组中的磁链极性与大小发生改变，从而产生感应电动势。

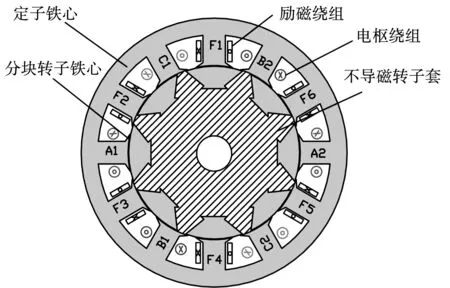
图1 传统ESFSG结构图Fig.1 Configuration of traditional ESFSG

假设ESFSG工作时励磁绕组F1～F6通入的直流励磁电流方向为图1所示的方向，且定义磁通穿入线圈时为正。以线圈A1为例进行分析，ESFSG工作时绕组匝链的极性交变如图2所示。

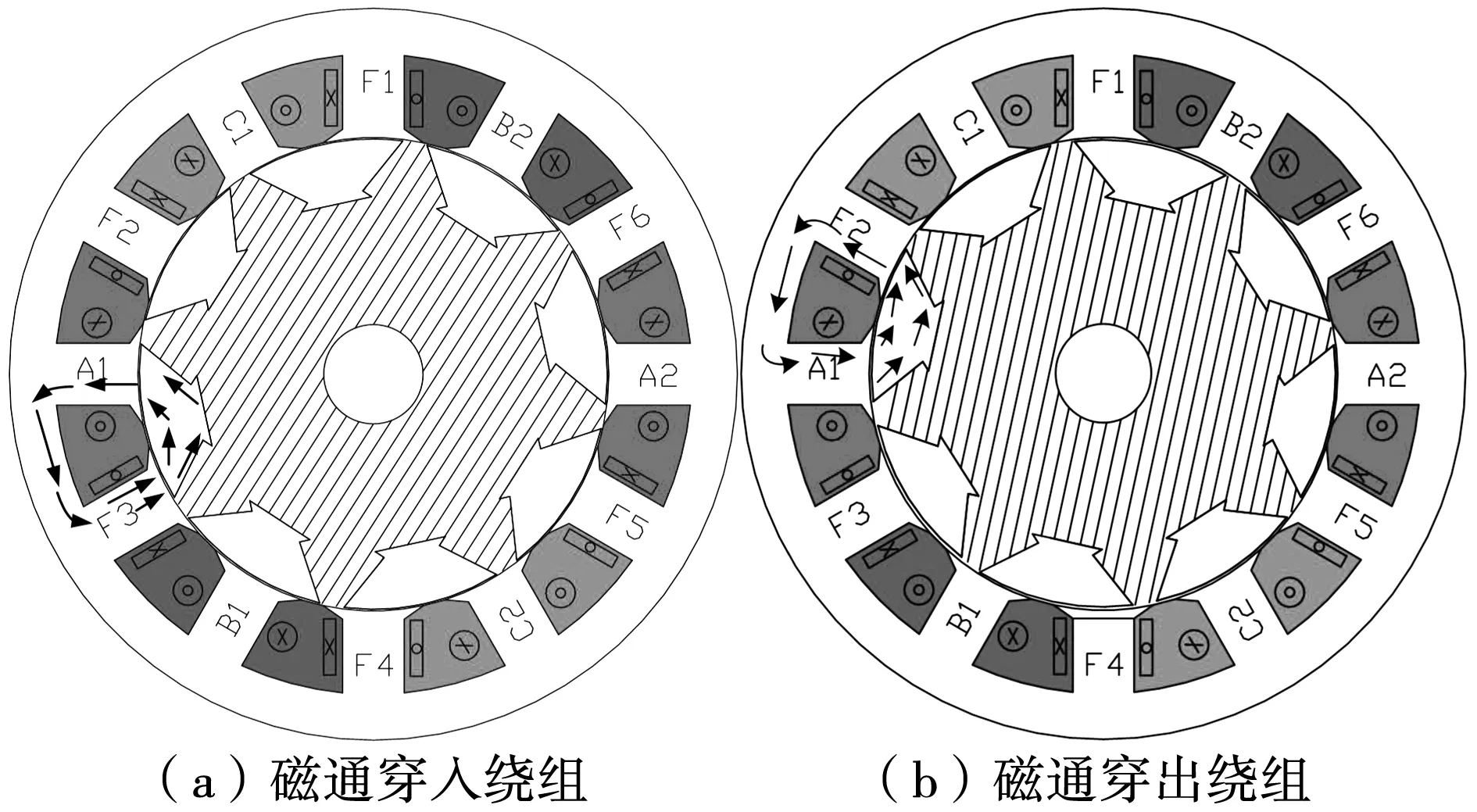
图2 ESFSG工作原理Fig.2 Operation principle of the ESFSG

由最小磁阻原理可知，当转子齿处于如图2(a)所示的位置时，磁通穿入线圈A1，即A1匝链正磁通；转子齿处于如图2(b)所示的位置时，磁通穿出线圈A1，即A1匝链负磁通；当转子连续旋转时线圈A1匝链的磁通正负周期变化，这就是ESFSG磁通切换的工作原理。

取12/7、12/8极电机转子极弧皆为0.866，其它结构参数相同，使电机转子逆时针旋转运动。由图3中电机定转子相对位置变化可以看出，12/7极电机的A1和A2两个线圈大小变化趋势随时间一致，即A1、A2的磁通正负变化是同步的，而12/8极正好相反，即A1和A2两个线圈磁通正负变化趋势相反[18]。

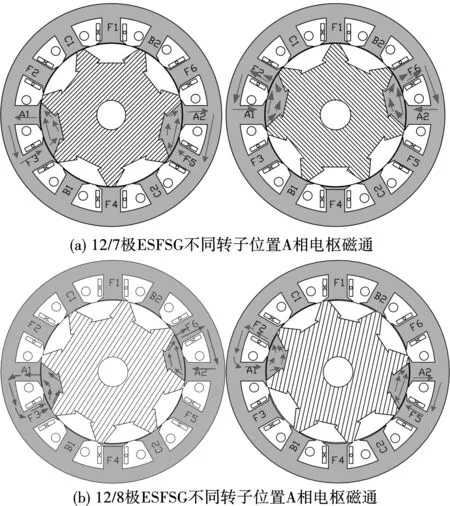
图3 ESFSG线圈磁通方向Fig.3 Flux direction of ESFSG coil

2 传统ESFSG空载特性对比

经过有限元仿真，给电机通10 A励磁电流，以3 000 r/min逆时针旋转时，从图4中可以明显看出12/8极电机的感应电动势在负半周期里出现突变，最高处的幅值为60 V，而最低处的幅值却为110 V，存在正负半周期不对称的问题。

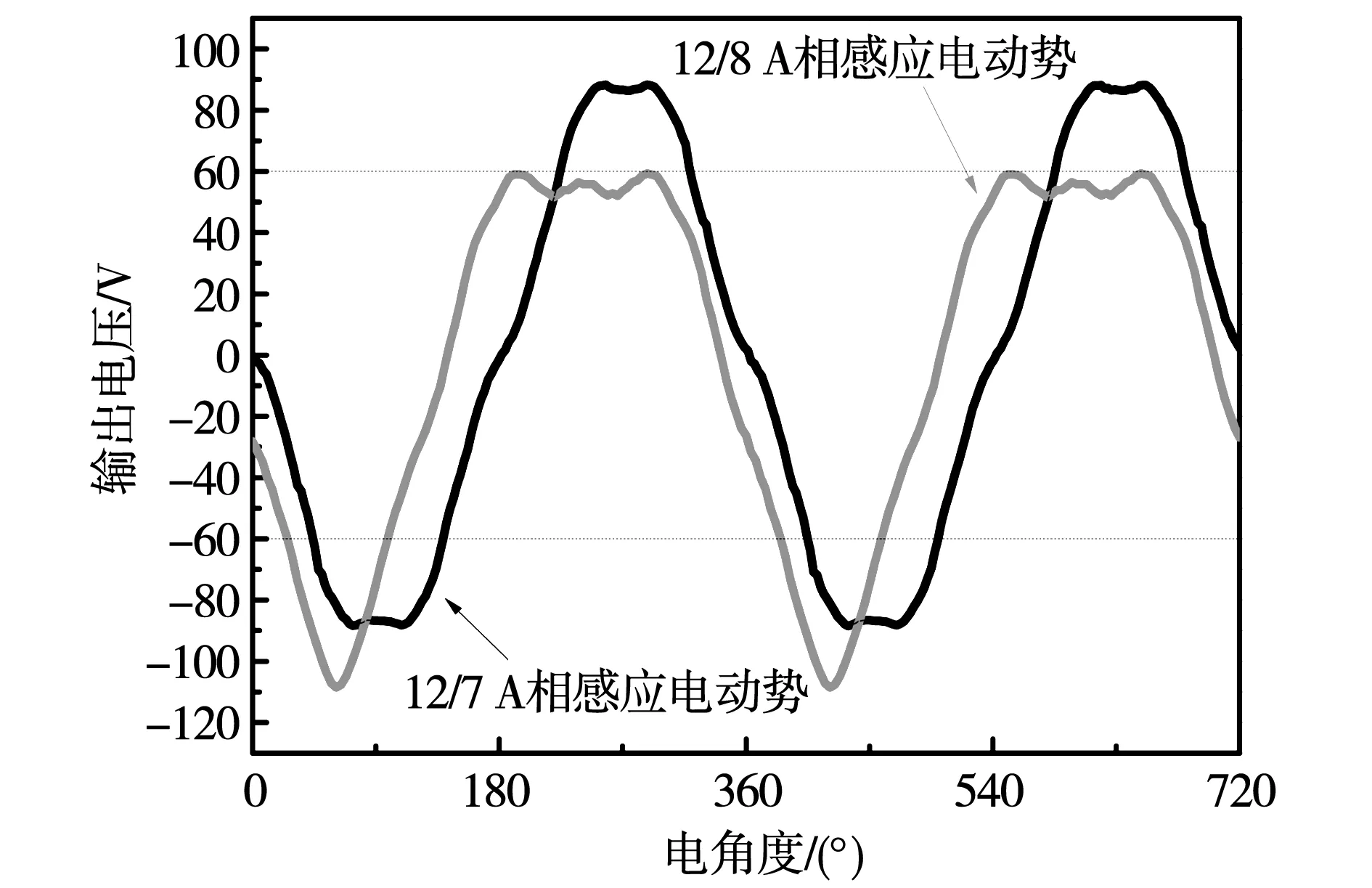
图4 ESFSG A相感应电动势Fig.4 ESFSG A phase induction electromotive force

两者A相电枢感应电动势谐波如图5所示，证实12/7极较12/8极存在感应电动势中没有偶数次谐波的优点。众所周知，若感应电动势中含有大量谐波，波形不是理想的正弦波，对于电动机，会降低控制精确度，增加损耗和转矩脉动；对于发电机，则会降低发电的效率。

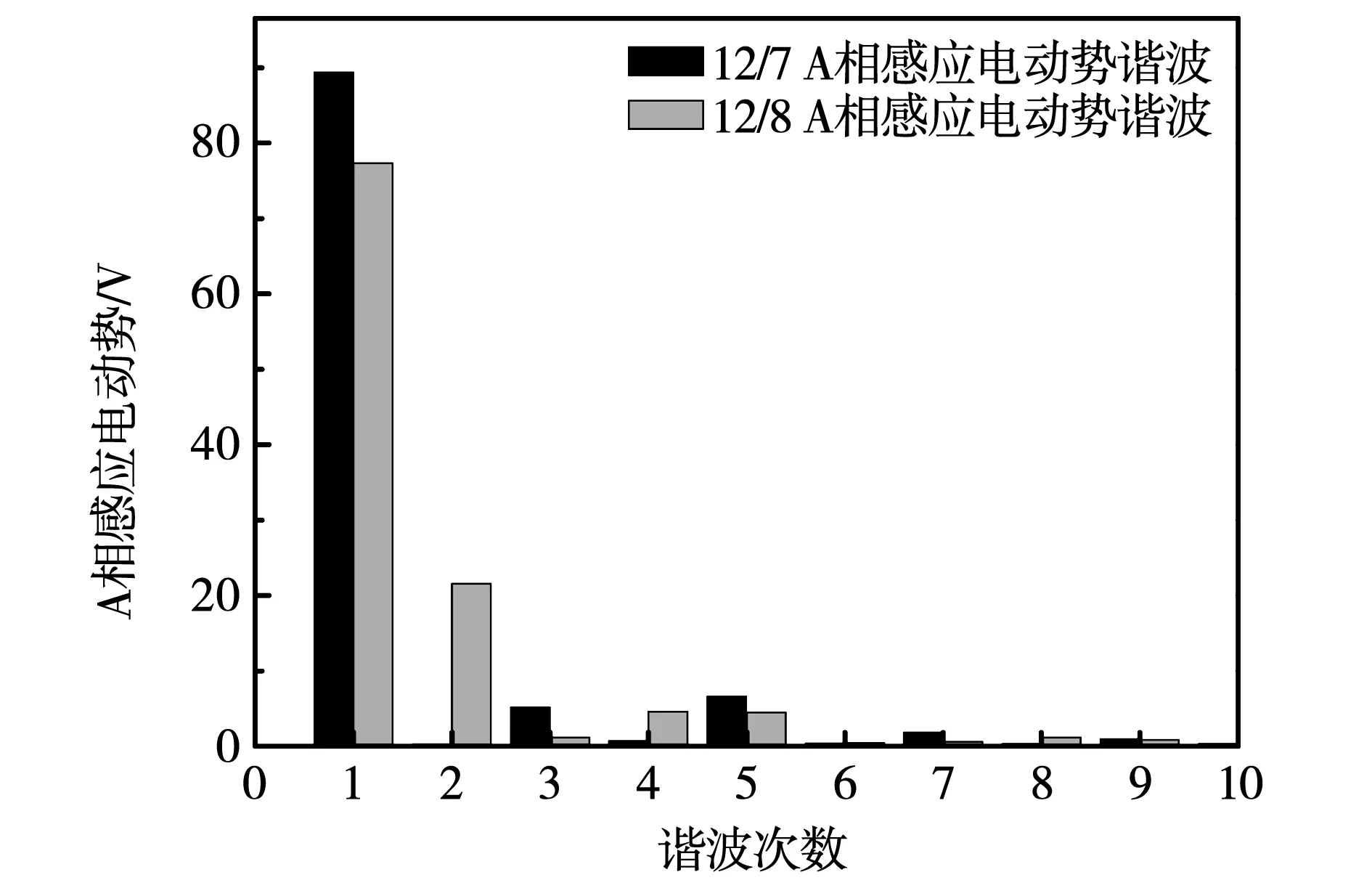
图5 12/7与12/8 A相感应电动势谐波分布Fig.5 Harmonic distribution of 12/7 and 12/8 A phase induced electromotive force

3 新型ESFSG电枢绕组磁链的计算

选择在沿分块转子切向添加气隙磁障的方式来增大转子的交轴磁阻，通过交直轴磁阻的差异来限制磁通路径，使定子磁动势不能在转子的任意方向上随意作用，从而达到谐波调制的目的。新型ESFSG拓扑如图6所示。

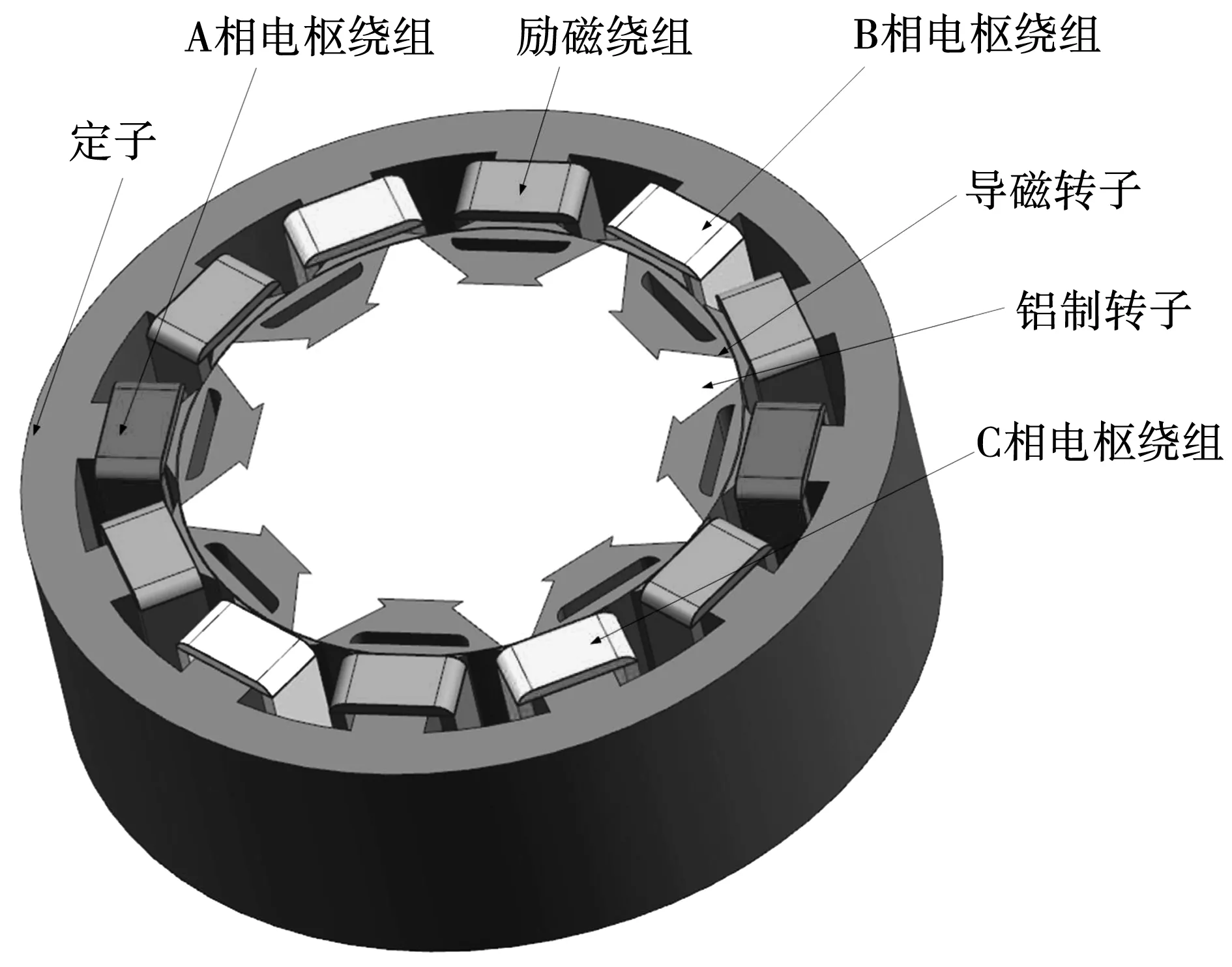
图6 新型ESFSG拓扑Fig.6 New ESFSG topology

本文介绍一种数学解析方法，通过分别计算定、转子侧磁势得到气隙磁压降，进而计算得到磁链及感应电动势。

为了便于分析，作以下假设：

1)不计磁路饱和、磁滞和涡流的影响；

2)定子内表面光滑，忽略定子齿槽对气隙的影响；

3)转子表面光滑、磁阻连续，在结构上分别以直、交轴为对称中心。

相邻的励磁线组绕向相反，因此励磁绕组产生的磁势呈梯形波状。一个N极和S极组成的励磁源对应的机械角为2π/3，即励磁周期为2π/3，峰值为Nfif，如图7所示。取定转子的极弧系数分别为0.833、0.866，则励磁磁势可以表达为[19]：

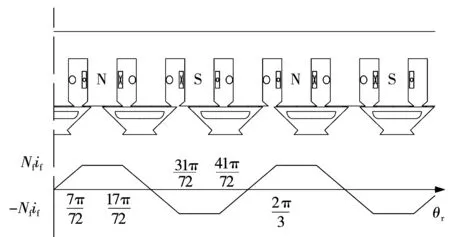
图7 励磁绕组产生的磁势图Fig.7 Magnetic potential generated by excitation winding

(1)

假设初始时刻t=0，q轴与A相绕组轴线重合，ESFSG分析模型如图8所示。

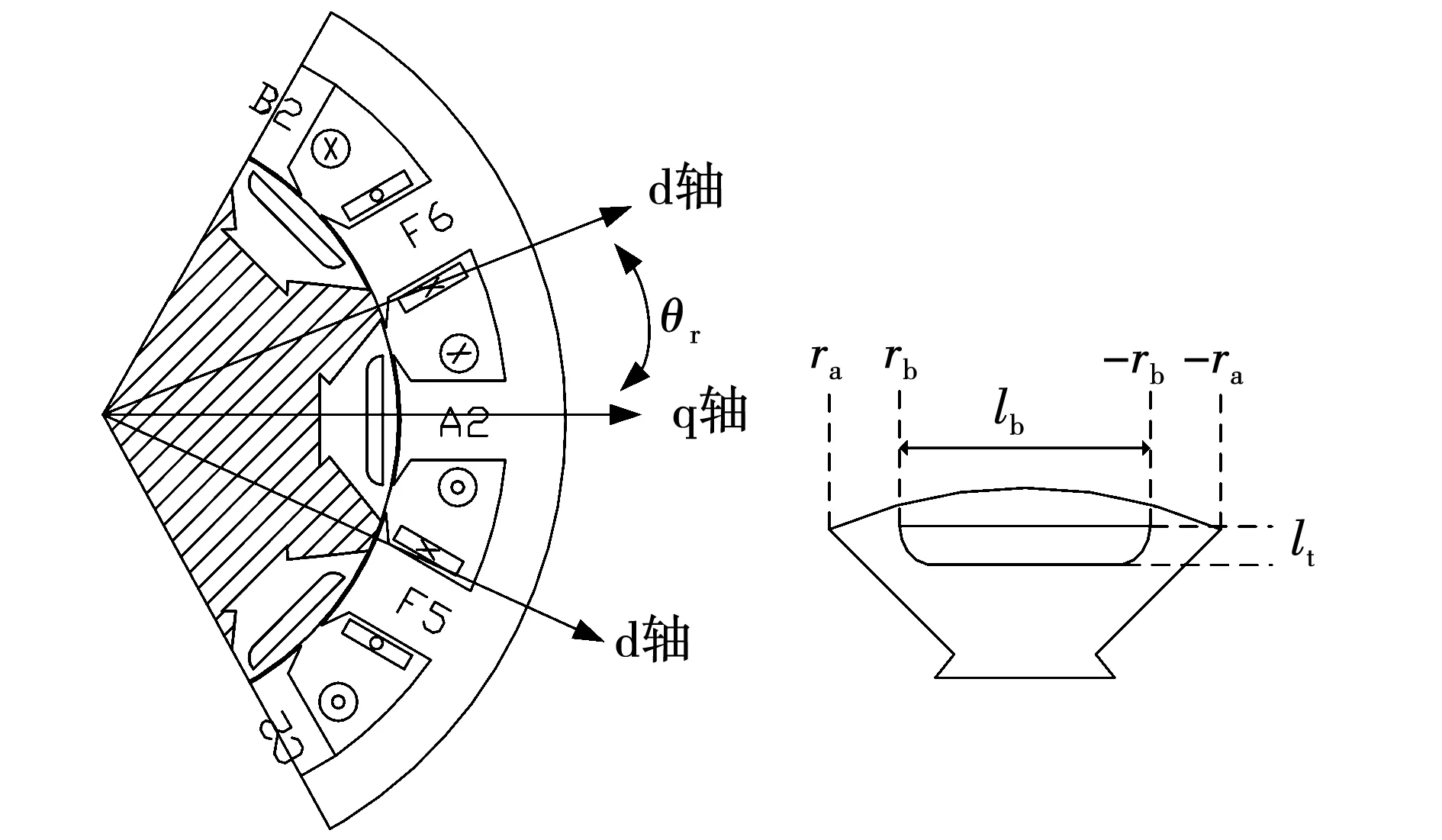
图8 新型ESFSG分析模型图Fig.8 New ESFSG analysis model diagram

切向气隙磁障的作用是减小定转子极之间流动的交轴磁通，同时它们允许直轴磁通很大程度地无阻碍直接流过磁极。

由于转子侧的磁势是由定子侧磁链产生的，因此转子磁势Fr(θr)的幅值仅随时间变化。在一个转子极距内，可以根据气隙磁障将转子磁位分为3个部分：左侧极端(ra,rb)、气隙极身(rb,-rb)、右侧极端(-rb,-ra)。在电机逆时针旋转时，虽然转子极两端磁导相同，但是由于两端磁通进出侧方向的不同，假定两者磁势相反。

转子两侧极端的磁导μr仅视为磁体本身磁导率，转子在气隙极身(rb,-rb)范围内的磁导Prb可计算为[20]

(2)

其中：μ0表示空气磁导率；lb表示磁障气隙宽度；lt表示磁障气隙高度；lst表示电机轴向长度。

经过转子极部分的磁通量φr等于气隙磁密在转子极弧范围面积内的积分，同时也等于转子磁势与磁导的乘积。因此，计算公式可表示为[20]

(3)

其中：g为气隙长度；nr为转子极数；r为定子内半径尺寸。

从而联立公式可以得到转子磁势Fr(θr),根据式(4)可以得到气隙磁密

Bg(θr)=[Fs(θr)-Fr(θr)]μ0/g。

(4)

以A相为例，主磁链可计算为[21]

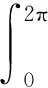
(5)

式中Na(θr)是电枢绕组的相绕组理想函数，表示为

Na(θr)=Nacos(θr+ω1t)。

(6)

其中：Na表示A相电枢绕组匝数；ω1表示电机机械角速度。

故A相感应电动势可得出

(7)

通过建立的简便解析模型，由式(1)、式(3)、式(4)和式(5)，当转子旋转时，通过ESFSG不同位置的定转子磁势的计算，能够快速得到气隙磁密和磁链。电枢绕组磁通量的改变将会使发电机产生感应电动势。

4 有限元仿真与样机实验

利用磁场有限元软件Maxwell建立了三相12/8极新型ESFSG模型，结构参数如表1所示，仿真得到的空载磁场如图9所示。

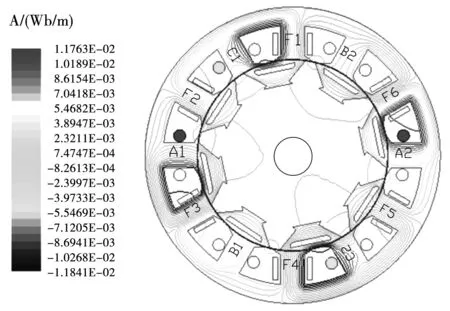
图9 12/8极新型ESFSG磁力线Fig.9 Magnetic flux lines of the new 12/8-pole ESFSG

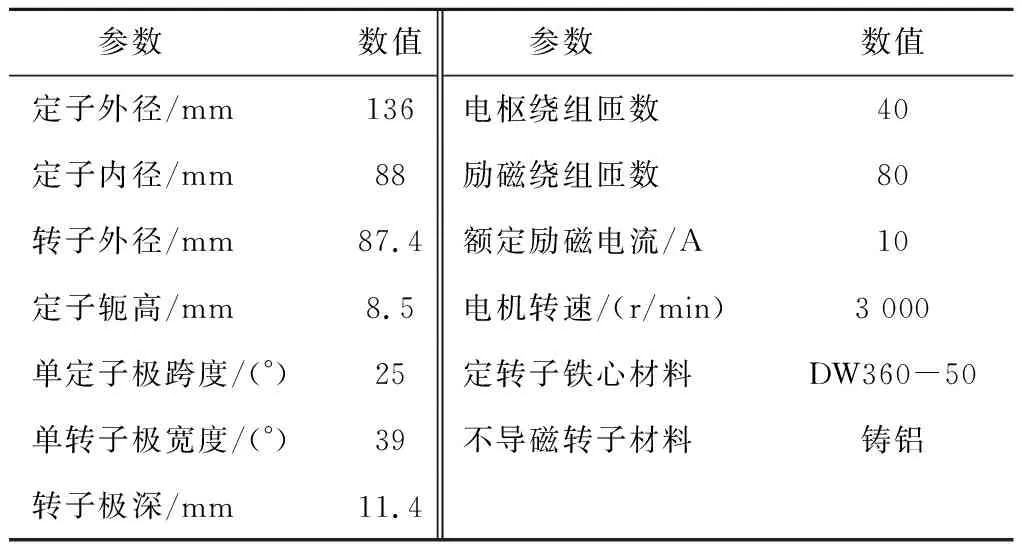
表1 三相新型ESFSG主要参数

选用励磁电流分别为5A、10A时得到新型ESFSG与传统ESFSG的感应电动势波形对比图，从图10中可以看出，新型ESFSG在分块转子上加入气隙磁障后，空载感应电动势波形趋于正弦波，正负半周期波形较传统ESFSG已近乎中心对称。

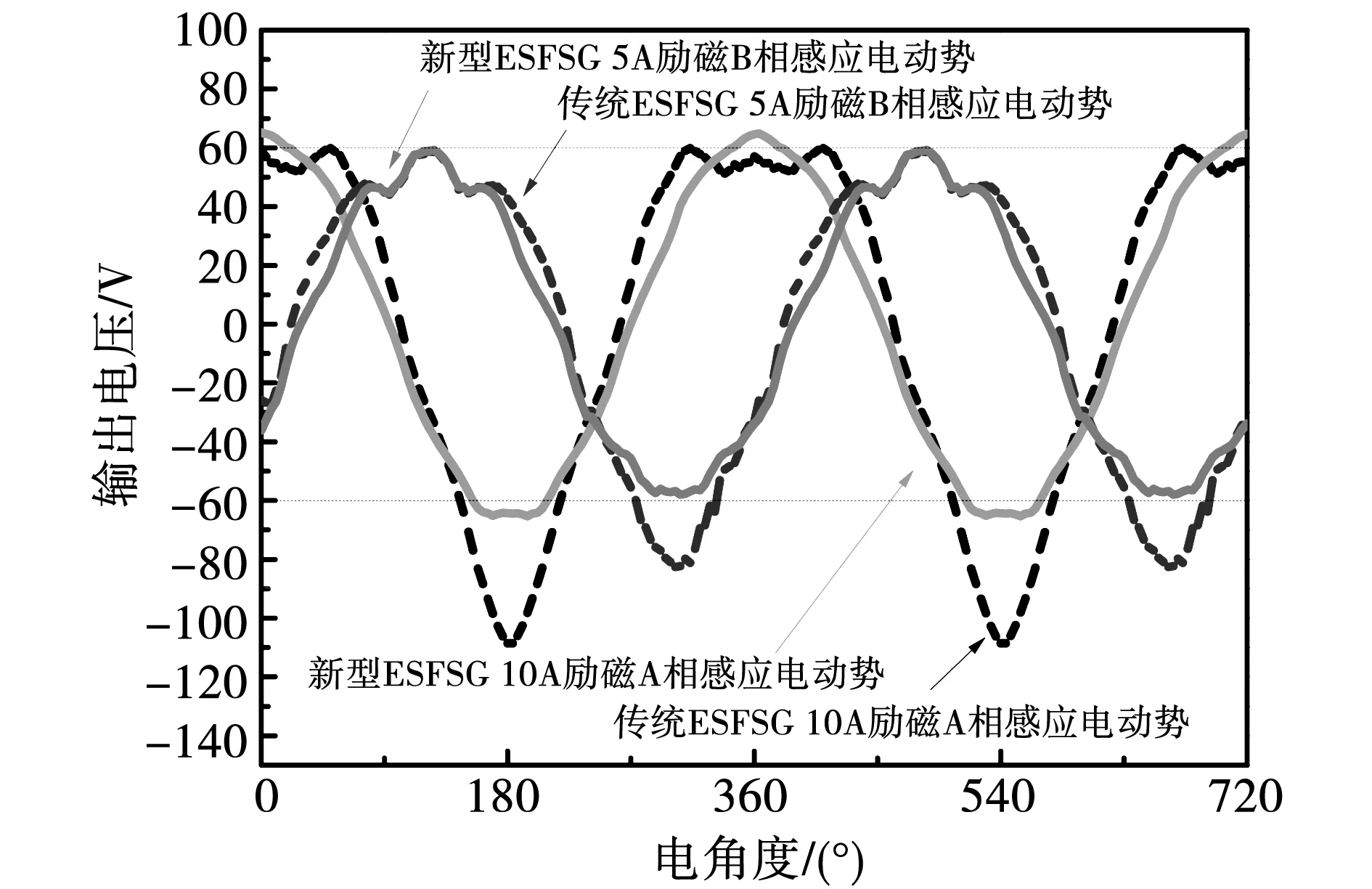
图10 不同励磁电流下的一相感应电动势对比图Fig.10 Comparison diagram of one-phase induced-electromotive force under different excitation current

采用曲线拟合的方法可以解析得到A相感应电动势的拟合曲线，将其与有限元法所得结果一同放置在图11中加以比较。由于解析法忽略了铁心磁压降，计算所得结果大小相比有限元法存在一定的误差。总体来看，解析法与有限元法得到的电机A相感应电动势具有相同的趋势且吻合度较高，即所采用的解析法可以用来分析新型ESFSG的静态特性。

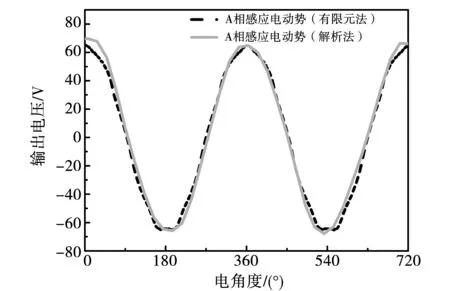
图11 解析法和有限元法对比图Fig.11 Comparison between analytical method and finite element simulation

从图12中可以看出，新型ESFSG可以明显削弱电枢绕组感应电动势的偶次谐波，从而在根本上解决感应电动势波形正负半周期不对称问题。但考虑谐波削弱效果的同时应兼顾基波的变化，用电压波形正弦畸变率KM来衡量优化方法对感应电动势波形谐波的削弱程度以及波形接近正弦的程度。

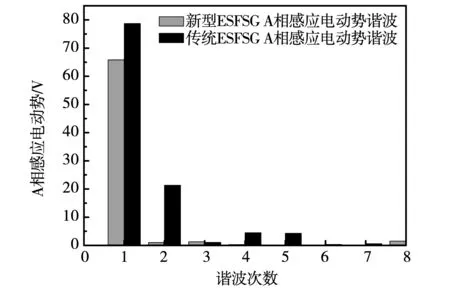
图12 A相感应电动势谐波对比Fig.12 Harmonic contrast of A phase induction electromotive force

对传统的ESFSG与本文的ESFSG进行傅里叶分解，取前10次谐波计算相绕组的总谐波失真(total harmonic distortion, THD)，并分离出奇数次(UTHDOOD)和偶数次(UTHDEVEN)谐波含量。结果如表2所示，具体公式如下：

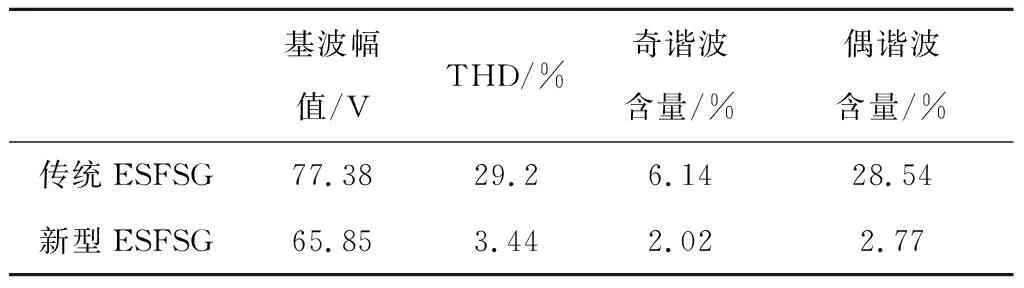
表2 ESFSG的谐波特性

(8)

其中ui为第i次谐波的幅值。

从表中数据可得，虽然本文ESFSG感应电动势基波幅值较传统电机减小了14.9%，但是本文电机感应电动势的电压波形正弦性畸变率降低了88.2%。以电机电枢绕组A相为例，从图13中能够看出，当励磁电流为10A时，新型ESFSG电枢绕组与励磁绕组在一个电周期内有着标准正弦的互感，而传统ESFSG的互感在一个电周期内非正弦，电感上升周期的时间比电感下降周期要长。并且新型ESFSG的自感也小于传统ESFSG，即新型ESFSG能够提高电机的容错性。

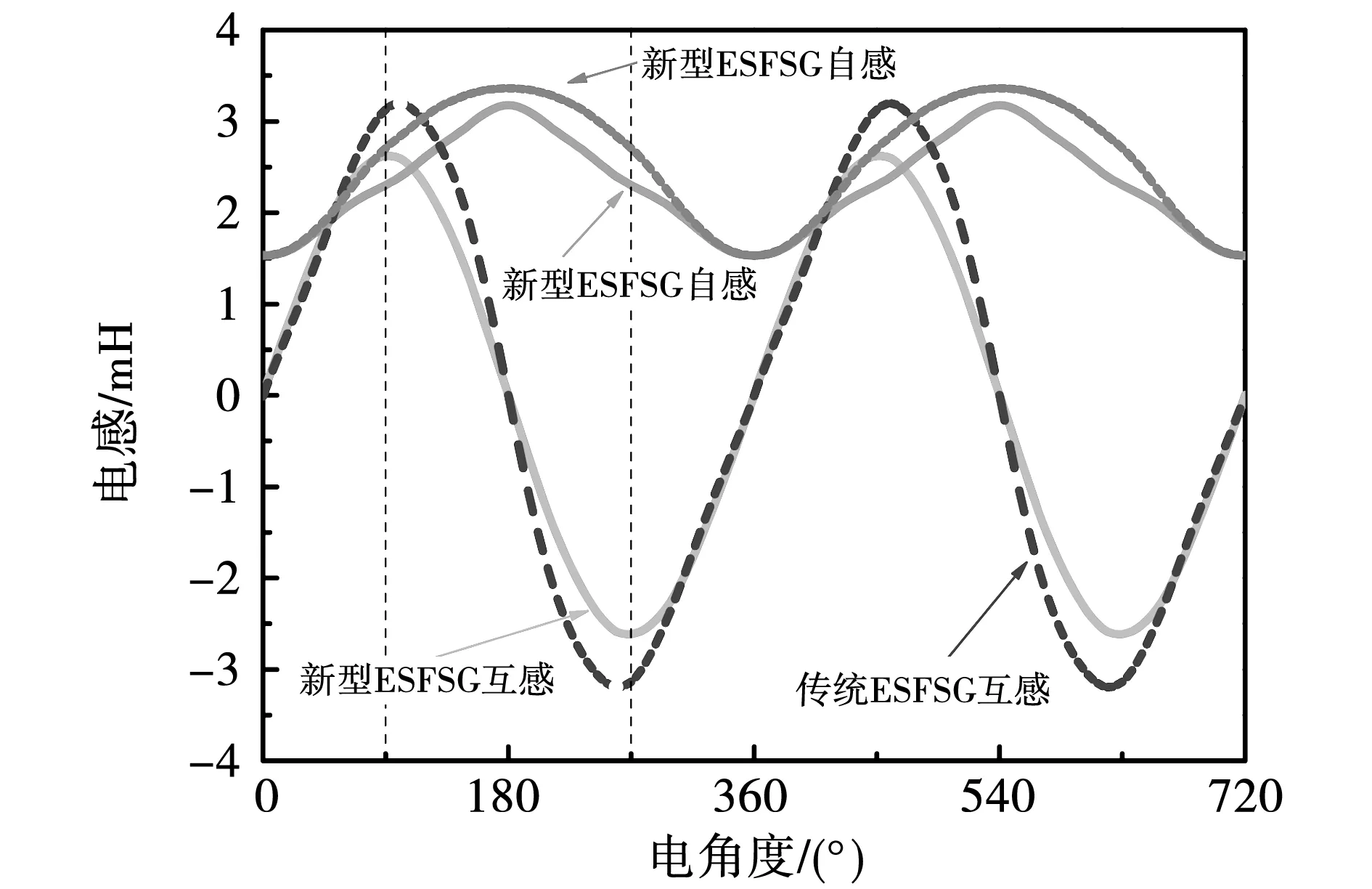
图13 ESFSG电感对比图Fig.13 Comparison diagram of ESFSG inductance

图14给出了对两种电机加以10Ω负载后得到的电动势和负载电流，通过波形可以看出，励磁电流为5A时，电机磁路未饱和，新型ESFSG与传统ESFSG的负载电动势波形吻合度较高，近似于方波。励磁电流为10A，电机磁路接近饱和时，在分块转子上开槽将会使得其负载输出电压有一定程度的降低。负载电流具有与负载电动势同样的变化趋势，即低励磁环境下，新型ESFSG与传统ESFSG负载电流波形一致，高励磁环境下，新型ESFSG的负载电流幅值低于传统ESFSG。可以认为在低励磁环境下，电枢反应将会对其有一定的增磁弥补作用。

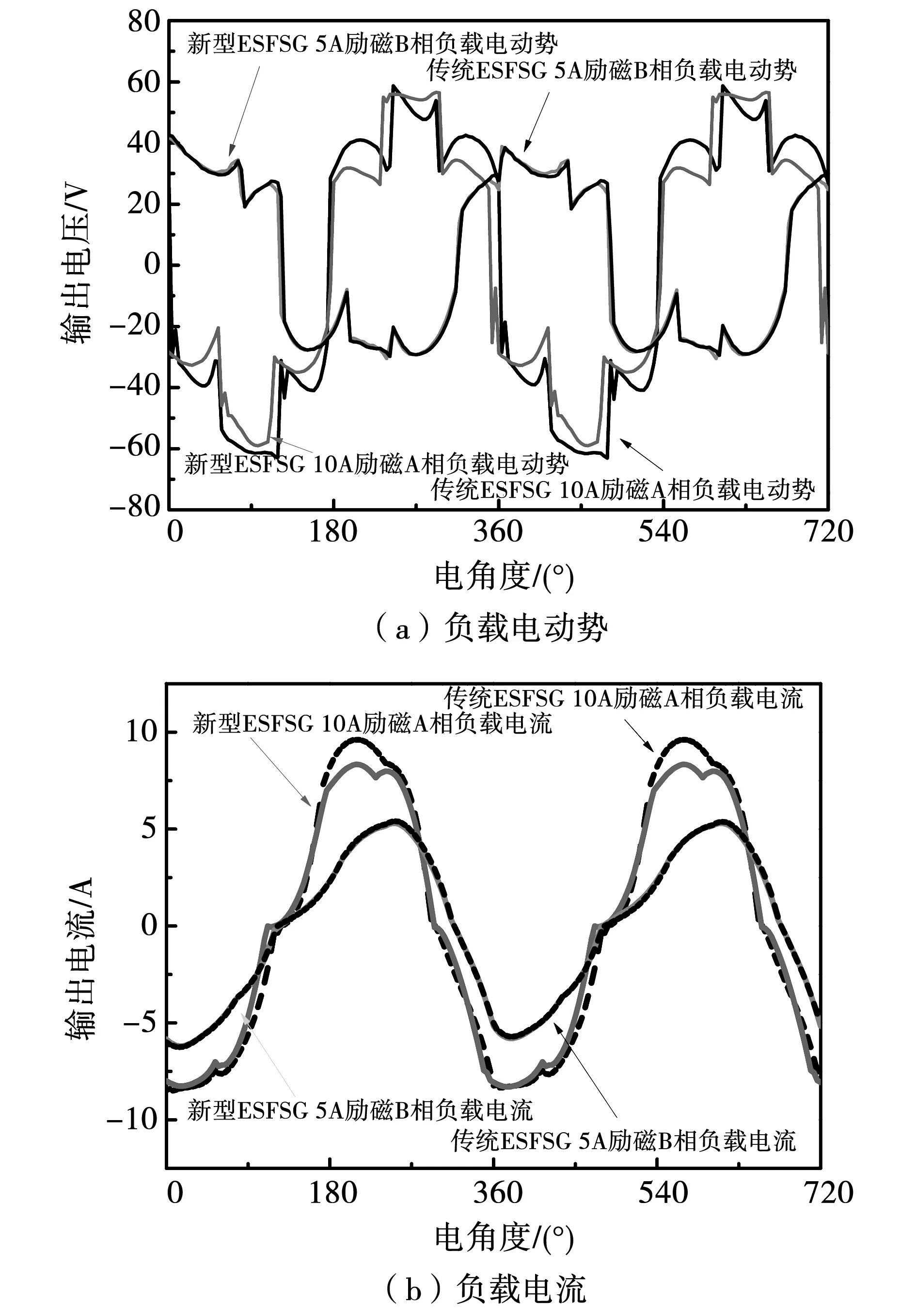
图14 ESFSG负载仿真波形Fig.14 ESFSG load simulation waveform

根据上述理论计算和仿真结果，按照表1中的主要参数试制了新型ESFSG,电机实物图如图15所示。对于新型三相ESFSG，输出电压很容易通过调整励磁电流的大小来调节，对其外加三相整流桥，发电机便可以输出直流电。图16用示波器给出了三相ESFSG在3 000 r/min时的三相空载和负载电动势。

图15 新型三相ESFSG定转子Fig.15 Stator and rotor of the new three-phase ESFSG

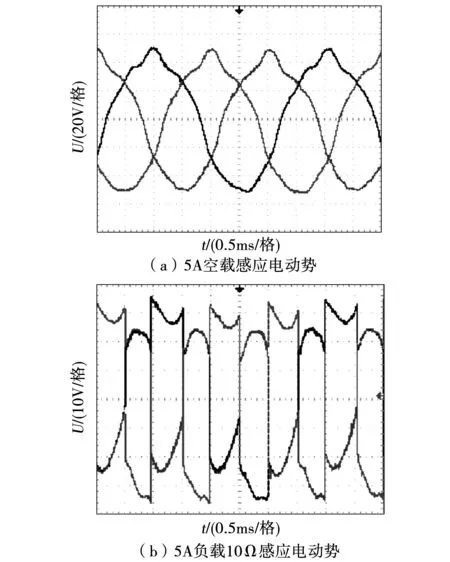
图16 三相12/8极ESFSG实验波形Fig.16 Experimental waveform of three-phase 12/8-pole ESFSG

由于制造工艺和实验条件的限制，导致空载感应电动势波形并不是完美的正弦波，负载感应电动势存在脉动，因此需要使用滤波电路来提供恒定的DC输出电压。但从总体上来看，仿真波形和实验波形具有相同的变化趋势，并且各相绕组的感应电动势具有相同的幅值，即充分验证了本文所介绍的新型ESFSG能有效减小偶数极分块转子磁通切换发电机感应电动势正负半周期波形不对称情况。

在3 000 r/min的转速下，调节励磁电流的大小，可得到ESFSG的空载特性图。从图17(a)中可以看出，当励磁磁势增加或者电机转速增加时，电机的输出电压也随之增加。因此，在电机处于不同转速时，只需调整励磁电流的大小即可保持输出电压的稳定性。

保持电机转速不变，选用励磁电流为5、8和10 A，并分别外接1、6、9、12、15和18 Ω的负载，得到发电机外特性图，从图17(b)中可以看出，当铁心饱和时，如励磁电流为8 A和10 A时，在输出电流较低时，两者的外特性曲线非常接近。

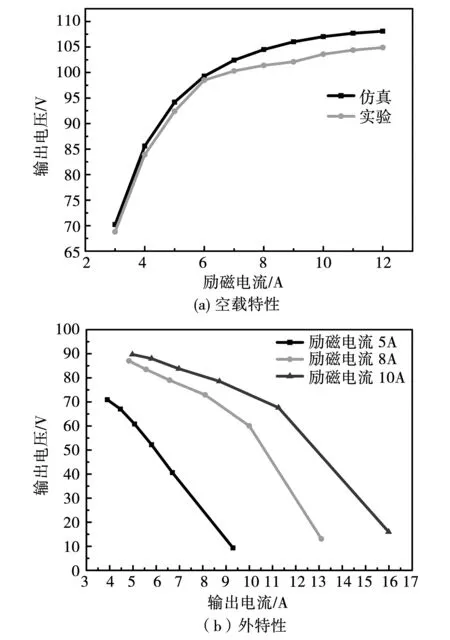
图17 空载特性和外特性实验Fig.17 No-load and external characteristic curves ESFSG

5 结 论

本文提出了一种感应电动势正负半周期对称的12/8结构分块转子磁通切换发电机。利用气隙磁压降解析法和有限元法对电机的电磁特性进行了仿真和研究，得到如下结论：

1)新型三相ESFSG采用分块转子上加开空气磁障的方法，能够降低空载感应电动势波形畸变率，解决传统三相ESFSG相感应电动势正负幅值不相等的问题，以达到改善发电质量的目的。

2)在计算新型ESFSG的定转子磁势时，可以将分块转子在气隙磁障处的磁导等效为气隙、磁体的磁导耦合，根据气隙磁压降得到的感应电动势和有限元得到的感应电动势具有相同的趋势，可以用来分析新型ESFSG的静态磁场特性。

3)由于切向气隙磁障的添加，虽然偶数极分段转子的偶数次谐波不能相互抵消，但是使得一相中两个线圈的谐波数值之和大大降低，进而使感应电动势正负半周期波形接近对称。

仿真和实验结果验证了本文设计谐波削弱方法的可行性和理论分析的正确性。