电动汽车永磁同步电机转子温度估计

朱元，肖明康，陆科，石其辉，吴志红

(1.同济大学 汽车学院，上海 201800；2. 同济大学 中德学院，上海 201800)

0 引 言

永磁同步电机因具有高功率密度和高转矩密度因而在电机汽车中得到了广泛应用[1-2]。车用电机控制器除了要求控制高精确度、高响应速度、调速范围宽、抗过载能力强以外，对其安全性也提出了更高的要求[3-4]。根据功能安全的要求，汽车电子电气系统的功能需要得到保证，由于软件和执行机构的系统故障和随机硬件故障导致的安全风险应该控制在可接受的范围内。为此，国际标准化组织，于2011年11月正式颁布了汽车电子电气系统的功能安全国际标准ISO 26262。而永磁同步电机本身的损坏通常是由于过热所导致。一方面，在长时间的电机运行过程中，电机定子由于焦耳损耗，导致大量热量在定子绕组中堆积，极易造成绕组的烧毁。另一方面，由于铁心损耗的存在，在电机高速运行时，涡流和磁滞损耗也会导致永磁体温度的升高，一旦到达永磁体的居里温度之后，就会导致永磁体的永久性失磁。为了防止电机过热损坏的情况出现，需要对电机温度进行监控。在目前的新能源汽车的永磁同步电机中，一般都埋设了检测定子温度的温度传感器。但由于转子是活动组件，无法对其温度进行直接检测，所以建立转子温度估计热模型对其温度进行实时监控尤为重要。

对于电机热分析的方法主要可以归纳为有限元分析法和集中参数等效热模型法。有限元分析的方法主要用于理想条件下电机的热分析，其精确度受到电机模型精确度及边界条件设置的影响，并且计算复杂，无法在汽车嵌入式系统中对转子温度进行在线估计[5-6]。集中参数热网络法是电机温度估计的常用方法，将电机热模型转化为等效电路模型[7-8]。主要的难点在于如何构造电机热模型，在能真实反映电机内部热量流动的前提下，能兼顾到汽车嵌入式系统的实时性要求以及控制器的成本限制[9]。

针对在电动汽车上的应用，少节点简化热模型被提出用于实时预测电机转子温度[10]。Christian Kral提出了三节点等效热模型，考虑到永磁体、定子线圈和定子铁心处的传热情况，用于估计永磁体和定子线圈温度[11]。Huber建立了以定子线圈，定子端部线圈和永磁体为节点的三节点简化热模型[9]。Wallscheid提出了四节点等效热模型，以定子轭部、定子齿部、定子线圈和永磁体作为温度节点[12]。但在模型建立过程中进行了较多的假设，只考虑到永磁体和定子线圈节点的温度，忽略了其他重要节点，比如端盖传热等，过于理想化，不符合电机实际的传热情况。其次，对热模型具体参数的辨识依赖于电机的结构参数和材料的传热特性，降低了系统鲁棒性，同时也会导致较大的计算量。

针对以上问题，本文对基于传热学原理搭建的电机集中参数模型进行了简化，提出了一种五节点集中参数等效热模型，选择了冷却液温度、电机定子温度、电机转子温度、电机端盖温度和电机机壳温度作为主要的温度节点，符合电机实际的结构特点。为了避免对热模型具体参数的辨识，提高系统的鲁棒性，提出了一种基于多元线性回归模型的热模型参数辨识方法，该方法只用对状态方程参数进行估计。最后基于状态方程的温度估计算法，分别在堵转、低速和高速混合工况条件下对转子温度进行了预测。

1 等效热模型

1.1 基于传热学原理热模型

如图1所示，从内置式永磁同步电机结构上进行分析，电机主要由水冷系统、机壳、散热水套、定子绕组、定子铁心、气隙、永磁体、转轴等组成。

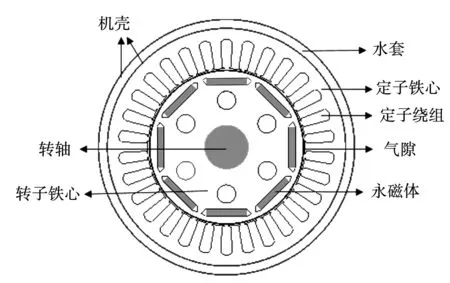
图1 内置式永磁同步电机截面图Fig.1 Sectional view of built-in permanent magnet synchronous motor

Mellor提出将电机组件转化为同心圆柱体，并建立等效T网络模型[13]。以对电机外壳建模为例，介绍等效T网络模型。如图2所示，轴向和径向的热传导可表示为两个独立的三端网络。其中，上下两个端子表示轴向和径向的表面温度，而第3个端子表示该部件的平均温度。由于组件内部的发热会导致平均温度低于三端网络的中心点，所以使用两个具有负值的热阻R3a、R3r来表示。热阻参数表达式是基于该部件的尺寸和轴向或径向导热系数确定。

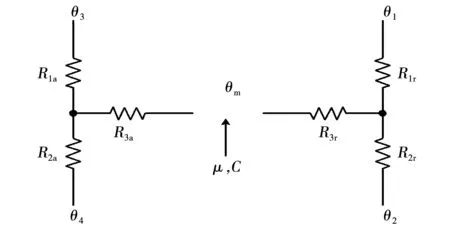
图2 独立的轴向和径向热网络模型Fig.2 Independent axial and radial thermal network models

图2中的参数的数学表达式为：

其中：L表示机壳长度，r1和r2分别表示机壳端面的外半径和内半径；ka和kr分别表示轴向及径向导热系数。

由于电机模型沿轴向对称，因此对模型进一步简化，将轴向热阻的三端网络合并为一个热阻Ra，如图3所示。

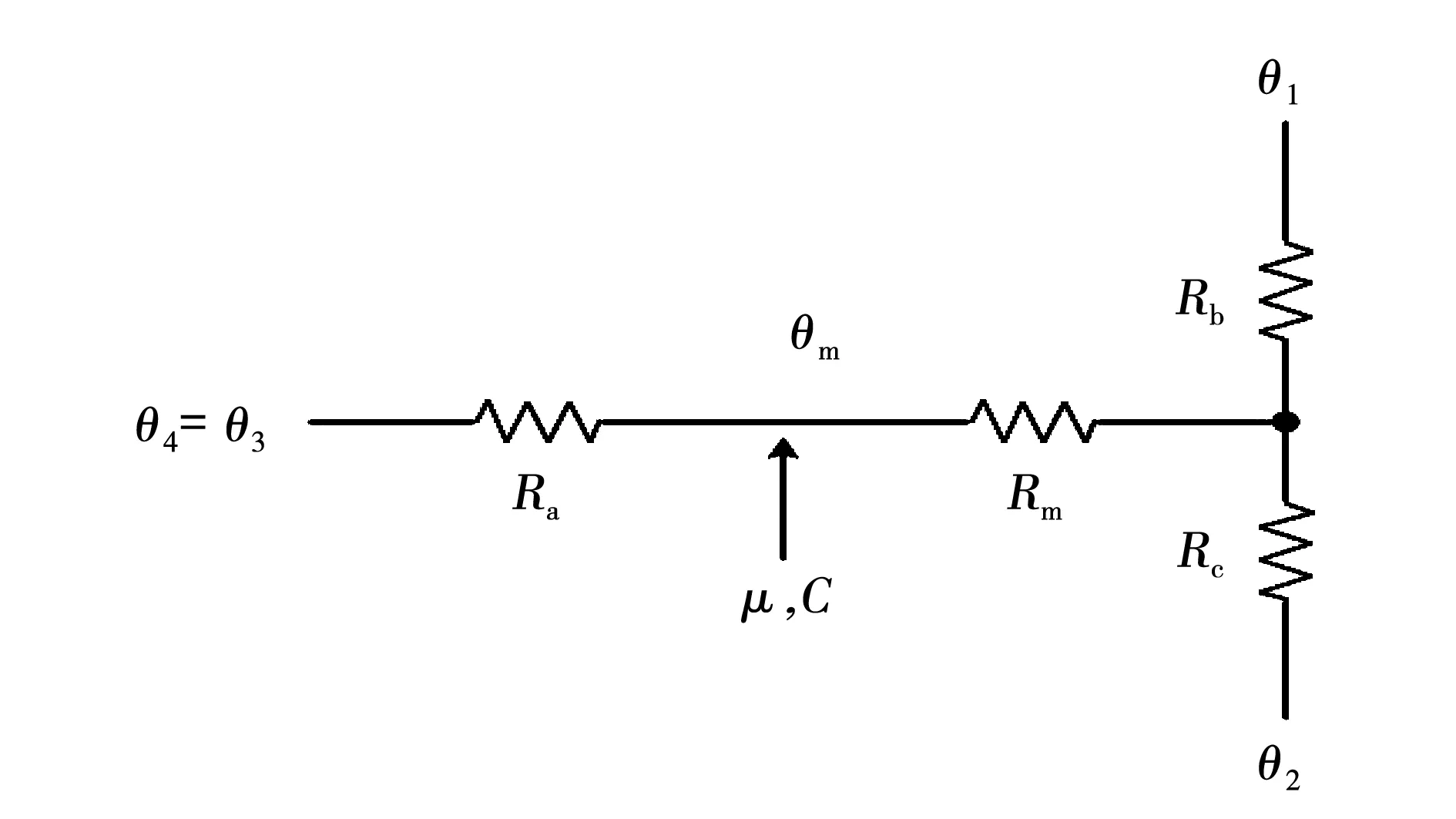
图3 对称部件的简化热网络Fig.3 Simplified thermal network of symmetricalcomponents

其中：

Ra=R1a+2R3a，

(1)

Rb=2R1r，

(2)

Rc=2R2r，

(3)

Rm=2R3r。

(4)

基于传热学原理和集中参数热网络法，对电机各部分进行建模，电机整体热模型如图4所示。每个部分对应的热模型包括热阻(图中Rx，热容(固体部分，图中Cx)和热源(有损耗的部分，图中Rx)，将这些部件的热模型按照热量流动的方向连接起来，形成总体的热网络模型。

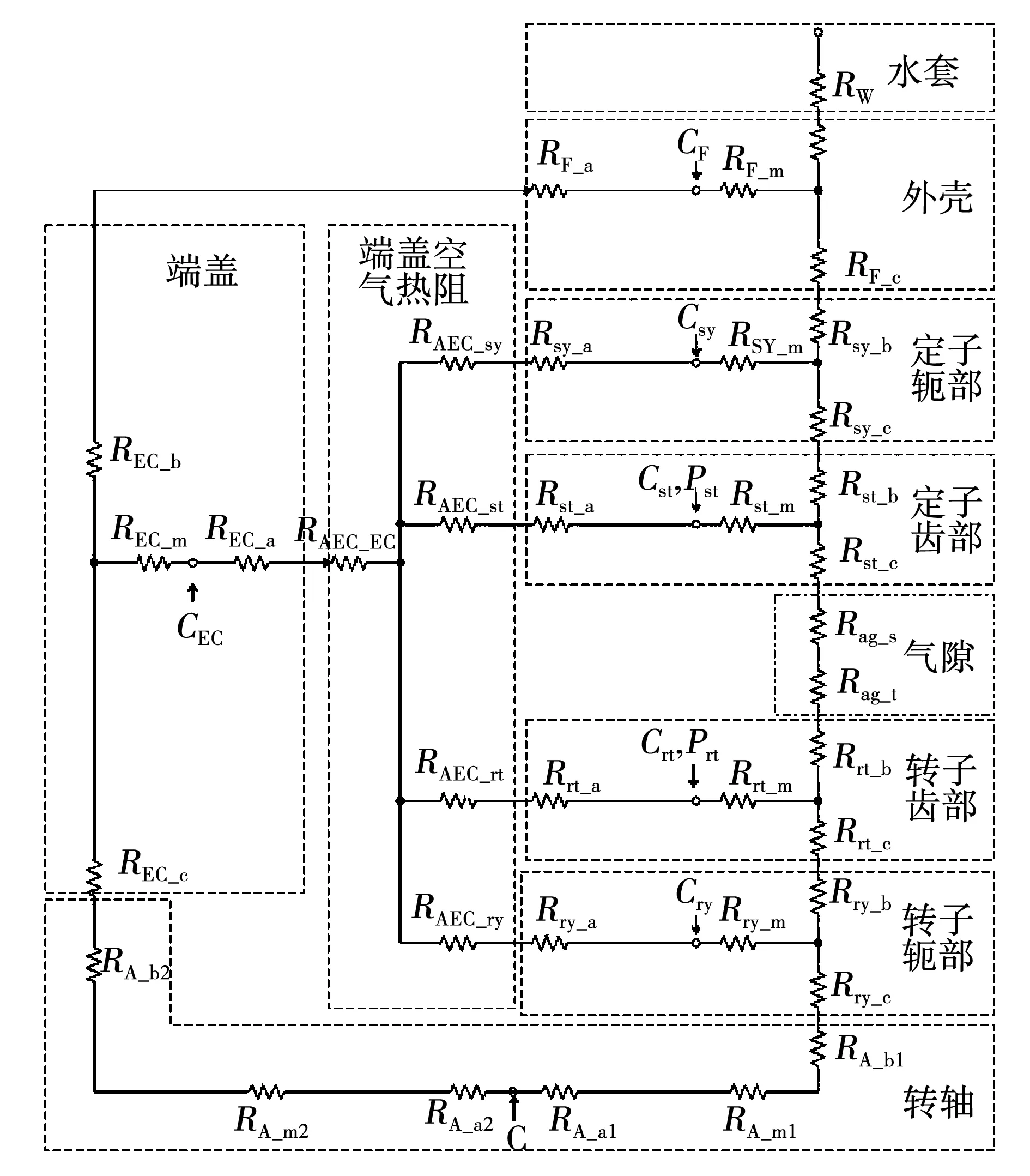
图4 基于传热学原理的电机热模型Fig.4 Motor thermal model based on the heat transfer principle

基于传热学原理的电机热模型可以对电机各部件温度进行估计，但该类方法存在如下不足：

1)高度依赖电机几何模型的精确度(组件的尺寸等)和材料的传热学特性(导热系数等)。在实际的工程应用中，较难完全获取相关的参数并保证较高的精确度。

2)流体模型精确度不理想。端盖空气热阻和气隙热阻的计算主要基于传热学的经验公式，但这些公式容易受到气隙尺寸、形状的影响，精确度有限。

3)热模型阶数高，不利于温度在线估计。由于对电机各组件分别建模，导致模型过于复杂，不利于在电机控制器嵌入式系统中实现。

基于上述原因，对基于传热学原理的电机热模型进行了简化，具体的简化过程如下：

1)只考虑转轴和槽内绕组的轴向传热，忽略端部空气热阻。其他部件只考虑径向传热。Boglietti研究了带有肋片的异步电机端部空气与外壳的传热情况，表明端部空气热阻远大于热模型中的其他热阻[15]。而研究的转子端面光滑的车用永磁同步电机，端部空气的散热效果更明显小于带有散热肋板的异步电机。所以，忽略端部空气热阻以简化热模型。

2)将T模型简化为同心圆壁模型。T模型由于考虑到节点温度和中心点温度的差异而引入了热阻Rm，虽提高了模型精确度但也使得模型变得复杂。将T模型与同心圆壁模型进行对比，发现在外径/内径比小于1.2时，模型误差小于5%[15]。考虑到模型的简化有利于在汽车嵌入式系统中的实现，所以将热阻Rm忽略。

3)将分布节点进行合并。虽将节点细分更有利于分析组件内部的温度分布，但较多的温度节点不利于嵌入式系统中对温度的在线估计。如果不关心组件内部的温度分布，而更关心某个特殊点的温度，可以在不影响关键节点的温度估计前提下，对模型进行降阶处理。

1.2 五节点简化热模型

在热模型节点的选择上，简化模型选择了冷却液温度、电机定子温度、电机转子温度、电机端盖温度以及电机机壳作为主要的温度节点。这样选择的主要原因是：

1)冷却液作为电机与外界进行热交换的主要方式，是电机外部的重要热源，同时在实车条件下，电机控制器通常会对这个温度进行采集；

2)电机定子则包含了电机外壳、定子铁心和定子绕组，这几个部分紧密相连，几何结构复杂，将其作为一个节点处理，可以大幅简化模型的复杂程度，同时电机定子也是电机内部的重要热源；

3)电机转子包含了电子转子铁心、永磁体和电机轴，这部分与电机定子间通过气隙隔开，与其他部分相对独立，同时转子铁损也是一个重要的内部热源；

4)电机端盖部分一方面与电机定子连接，另一方面又通过轴承和端盖空气与转子进行热交换，所以也将其独立成为一个节点。

5)电机机壳是将冷却系统、电机定子和电机端盖连接起来的中间部件，是热路中的重要节点。

根据上述的简化方法,所建立的简化电机热模型图5所示。

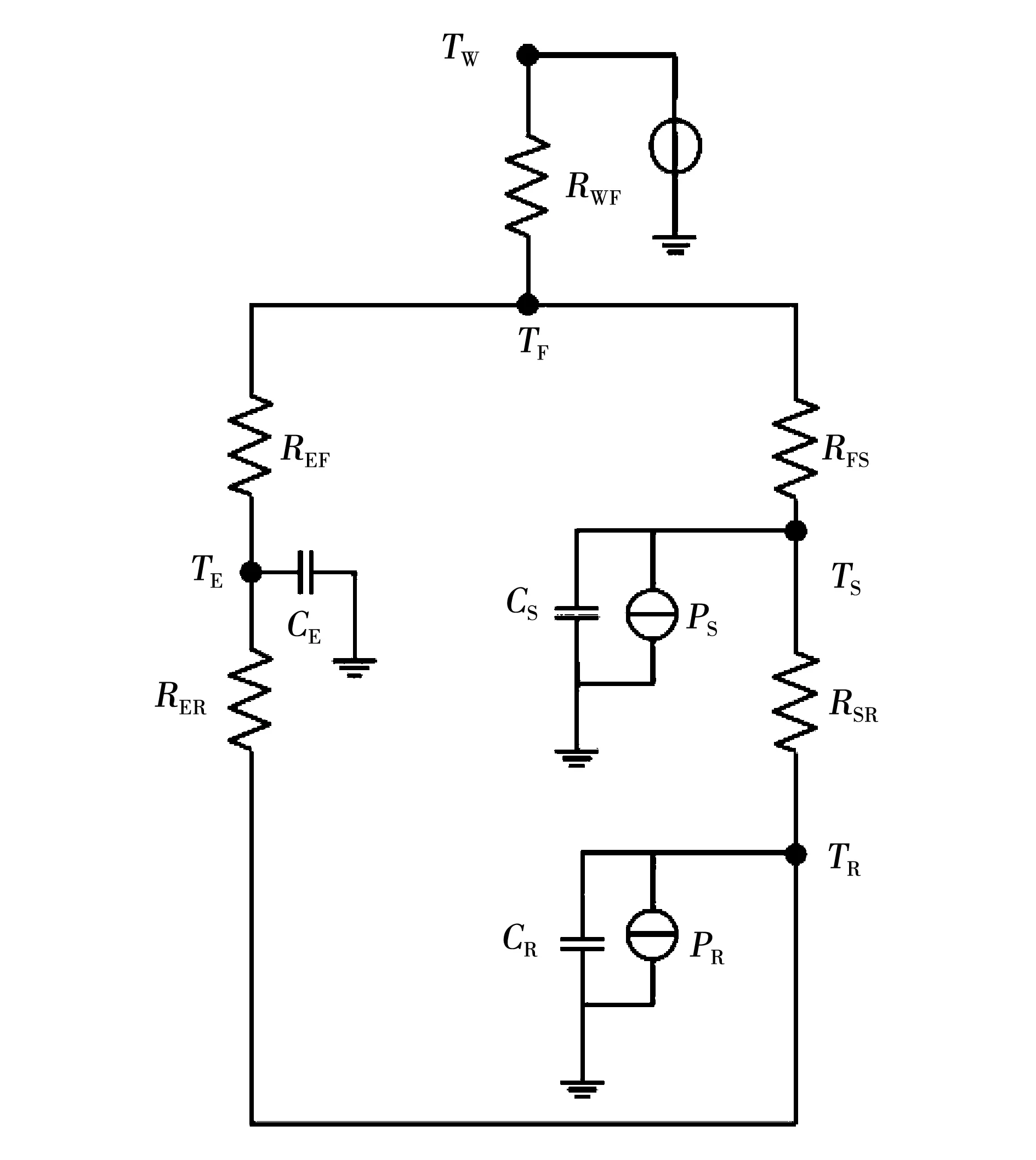
图5 五节点简化热模型Fig.5 Five-model simplified thermal model

图中：Tw表示冷却液温度；Ts表示电机定子温度；TR表示电机转子温度；TE表示电机端盖温度；RWF表示冷却液与电机外壳之间的热阻；RFS表示电机外壳与电机定子之间的热阻；RSR表示电机定子与电机转子之间的热阻；RER表示电机转子与电机轴承之间的热阻；REF表示电机轴承与电机外壳之间的热阻；CS表示电机定子热容；CR表示电机转子热容；CE表示电机端盖热容；而电机的热源主要考虑了电机定子和转子的损耗，分别定义为PS和PR。

1.3 数学建模

针对简化后的模型，比拟基尔霍夫电流定律，可以列出以下方程：

(5)

方程组包含了一个线性方程，对其进行求解

(6)

整理得到电机温度估计状态方程为

(7)

式中：

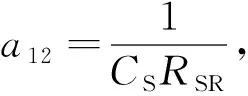
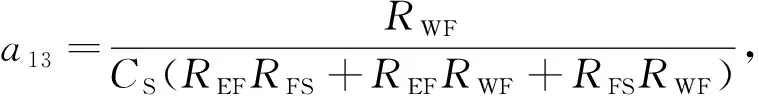
a33=

2 永磁同步电机损耗计算方法

在建立的电机简化模型中，电机绕组的铜损和分布于电机定子转子铁心中的铁损是电机内部的主要热源。作为电机热模型状态方程的输入，需要对这部分损耗进行在线计算。

定子铜损由定子电流和定子电阻确定。

铁损是温度模型的输入量，需要在温度估计过程中进行在线计算。等效电阻法因计算量小，易于在控制器软件中进行实现等优点，所以在铁损在线估计中广泛采用。在这种方法中，铁损被等效为并联电阻上的焦耳损耗，其大小正比于合成磁链的平方。但是在常规的等效电阻模型中，并不对定子和转子的热阻进行区分。但是在电机温度的估计中，转子铁损和定子铁损分别属于不同的节点。因此，本文提出了一种适用于电机温度估计的铁损计算方法。

等效电阻Rc可以看作是定子铁损等效电阻和转子铁损等效电阻并联的结果，分别定义定子铁损等效电阻和转子铁损等效电阻为Rcs和Rcr，则有

(8)

永磁同步电机输入电流经坐标变换后的轴电流id、iq分别由铁损电流icd、icq和磁化电流imq、imq组成。定、转子铁损分离的电机等效模型如图6所示。

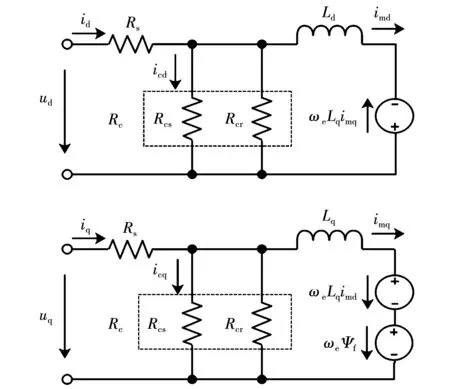
图6 定、转子铁损分离的永磁同步电机的动态d-q轴等效电路Fig.6 Dynamic d-q axis equivalent circuit of permanentmagnet synchronous motor with separated stator and rotor iron loss

(9)

电机的定、转子铁损功率分别:

(10)

(11)

定转子等效铁损电阻可以使用无负载情况下(imd=imq=0)的铁损进行计算。在无负载情况下，等效铁损电阻与转速的关系为：

(12)

通过有限元仿真的方法，可以对电机在不同转速下的铁损进行仿真计算，然后根据计算结果和公式(12)，即可以对电机的铁损电阻进行估计。其中，电机转子损耗包含了转子铁心损耗和永磁体损耗。

3 参数辨识与电机温度在线估计

3.1 状态方程参数辨识

第一节虽然对电机模型进行了简化，减少了参数的数量，但是对这些参数的计算仍然是一件非常困难的事情, 仍需要对热阻和热容等参数进行识别。这些参数虽然可以根据传热学原理进行大致估计，但这种方法的主要缺点是，需要大量的电机结构参数，且参数精确度难以保证。因此对于简化模型，提出了一种基于多元线性回归模型的热模型参数离线识别方法。该方法不用估计热模型参数，只需要估计状态方程中的参数。

对简化电机热模型的状态方程进行离散化之后可以发现，状态变量(节点温度)的时间导数是关于状态变量和输入(发热量)的线性函数，这使得使用多元线性回归的方法，对热模型的参数进行离线辨识成为可能。

回归模型一般形式为：

(13)

因变量Y是由yi组成的向量，因变量X是由xi组成的向量。yi可以近似地表示为自变量x1,x2,x3,…,xN的线性函数。β1,β2,…,βN为偏回归系数，ε是去除自变量对Y影响后的随机误差(残差)。

根据式(7)所提出的电机模型，定义：

(14)

(15)

则回归系数与电机热模型状态方程系数的对应关系可以表示为

(16)

使用normal equation对β进行无偏估计，可以有

(17)

根据电机各部分温度的采样结果和温度的变化率，即可对电机的参数进行估计。为了辨识电机的热模型参数，需要对电机的定子温度、转子温度、端盖温度和冷却水温度等进行采样。

考虑到电机热阻与转速的关系，选择若干转速，分别进行参数识别，再通过插值的方法，获得任意转速下的热模型参数。

3.2 基于状态方程的电机温度估计

在离线辨识状态方程中的参数后，通过采样冷却水温度和完成电机定转子损耗在线计算后，转子温度可以在线估计。基于电机状态方程对定子温度、转子温度和端盖温度进行在线估计算，即

(18)

因为转子温度过高会导致永磁同步电机永磁体永久失磁，对转子温度进行实时监控能提前降低运行负载，避免失磁现象的发生。所以，基于提出的五节点热模型和电机温度估计算法，对电机转子温度的估计准确性进行了实验验证。

4 实验验证

4.1 实验平台

为验证所提出热模型的准确性和有效性，在电机台架上进行了测试。实验使用的是一台4对极内置式永磁同步电机，电机参数如表1所示。

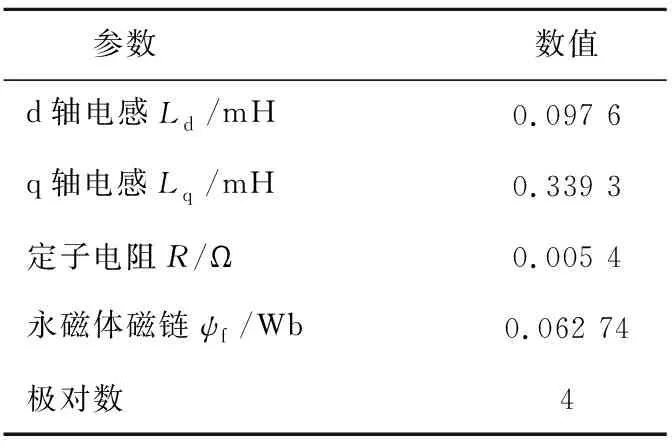
表1 电机参数

图7为所搭建的实验平台，主要包括测试电机与测功机、电机控制器、上位机和专用的温度采集设备。

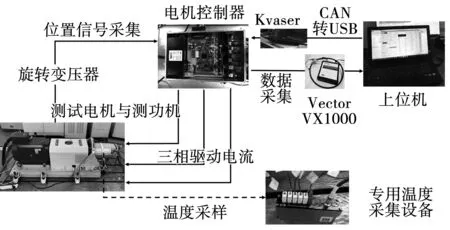
图7 实验平台Fig.7 Experiment platform

专用的温度采集设备对关键位置(定子绕组、机壳、端盖、转子)的温度进行采集，如图8所示。为了方便温度的采集，对电机进行了改造，在电机的机壳(内机壳和外机壳)、定子绕组(定子槽中部和定子绕组端部)和轴承外圈部位埋设了K型温度传感器，分别用于对电机机壳、定子绕组和电机端盖的温度进行采集。对于转子温度的采样，在转子磁钢端部安装温度传感器，使用了无线发射和接收设备，将内部的温度信号发射至外部接收装置。

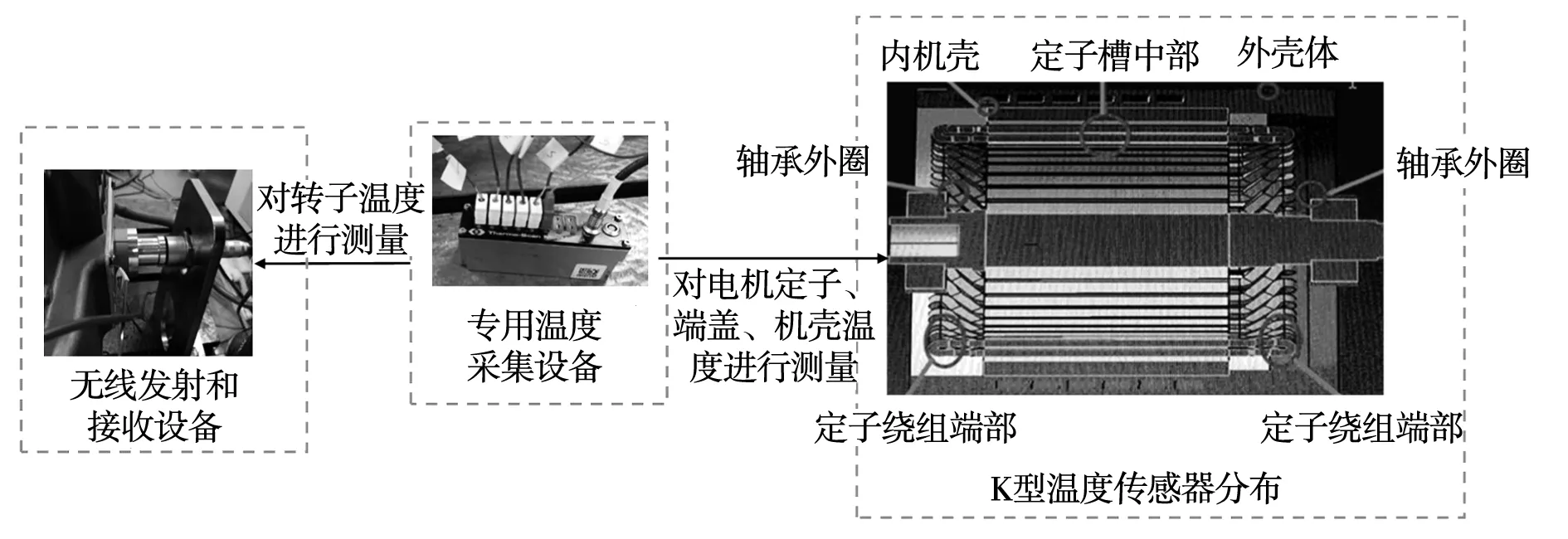
图8 温度采集设备Fig.8 Temperature acquisition equipment

4.2 堵转和低速条件实验工况

堵转和低速条件下的电机传热情况较为特殊，主要因为此时转子和定子间气隙空气流速较低，转子和定子间热阻较大。同时，定子三相电流发热也不均匀。因此，针对堵转和低速条件下的转子温度估计进行了验证，对电机在不同的时间范围内进行加减载实验，以验证所提出来的热模型的准确性。表2和表3分别表示堵转工况和5 r/min下的实验工况。图9和图10分别为堵转工况和5 r/min下的测量温度(传感器采集)与预测温度(基于状态方程估计)的结果对比。

表2 堵转实验工况

表3 5 r/min实验工况

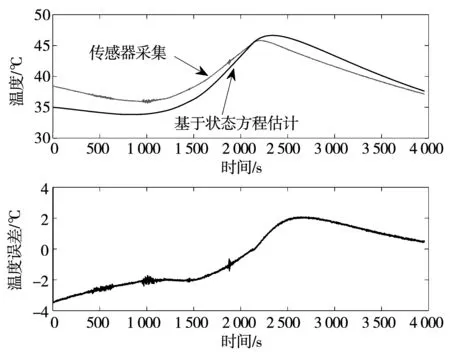
图9 堵转工况下转子温度估计对比Fig.9 Rotor temperature estimation comparisonunder the locked-rotor condition

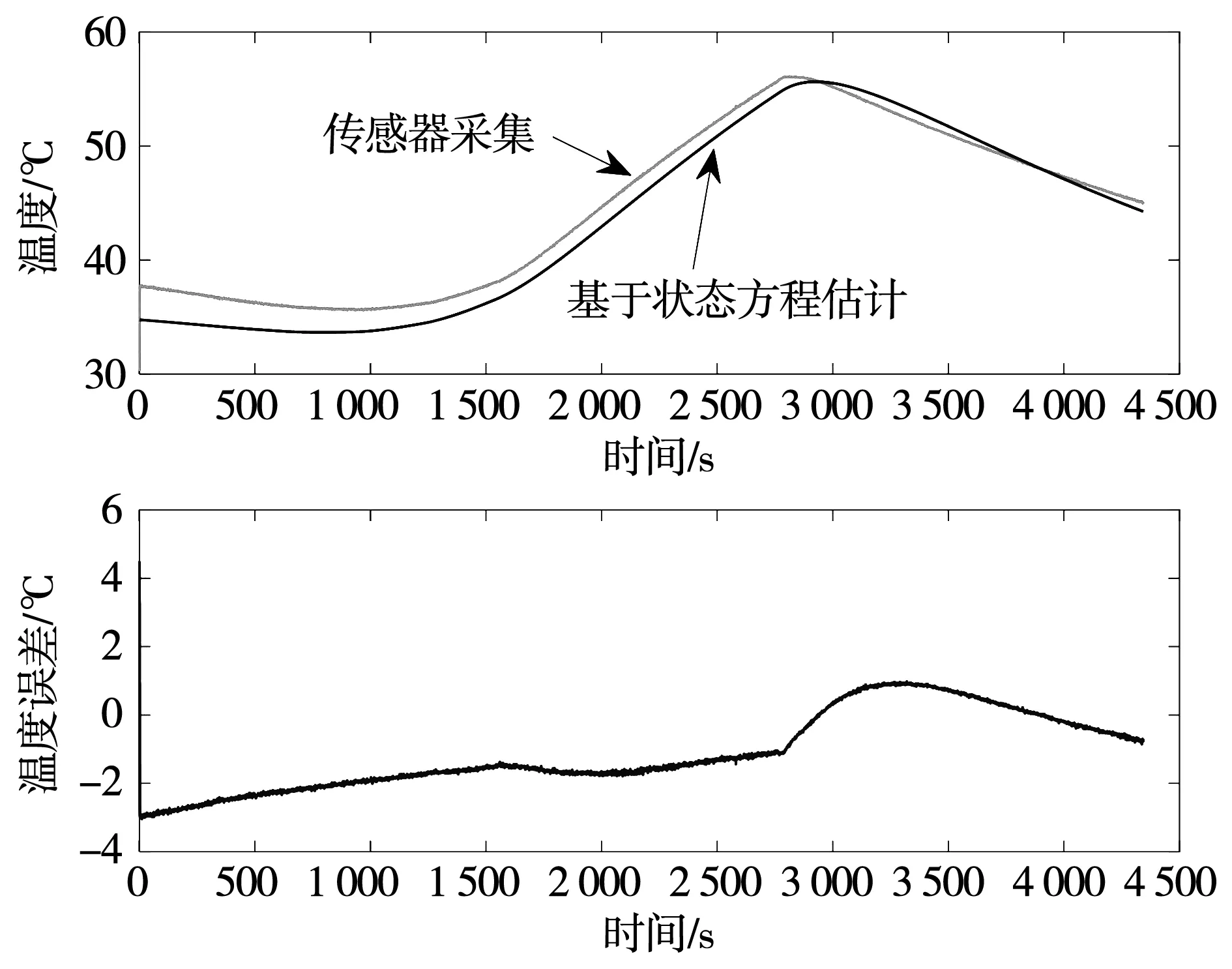
图10 5 r/min转子温度估计对比Fig.10 Rotor temperature estimation comparison at 5 r/min

实验中，分别对堵转和低速条件下的转子温度估计进行了对比。从实验结果可以发现，在这两种特殊工况下，基于状态方程预测的转子温度结果比较理想，最大估计误差小于4 ℃，这说明提出的热模型能够较好的反映电机转子的真实温度变化过程。从温度误差图可以发现，初始时刻温度误差较大，随着时间的推移，基于状态方程预测的温度能慢慢收敛到真实的测量温度，说明在堵转和低速工况下，误差主要来自于初始温度的设置。

4.3 高速混合实验工况

在完成堵转和低速实验工况下的温度估计算法验证后，为了进一步验证所提出来的热模型的正确性，进行了在不同转速和转矩下的实验，混合实验工况如图11所示。

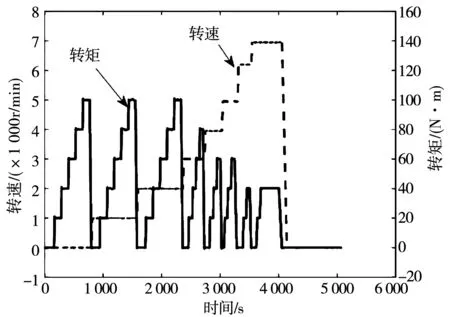
图11 高速混合实验工况Fig.11 Mixed experimental conditions

图12给出了混合实验工况下转子温度估计的对比结果。可以看出，在大多数工况情况下，转子温度估计误差在2 ℃内；在转矩变化较剧烈的时刻(转矩由最大值下降到0)，转子温度估计误差在4 ℃内；在4 000 s时刻，由于转速和转矩的突变，转子温度估计最大误差为6 ℃。

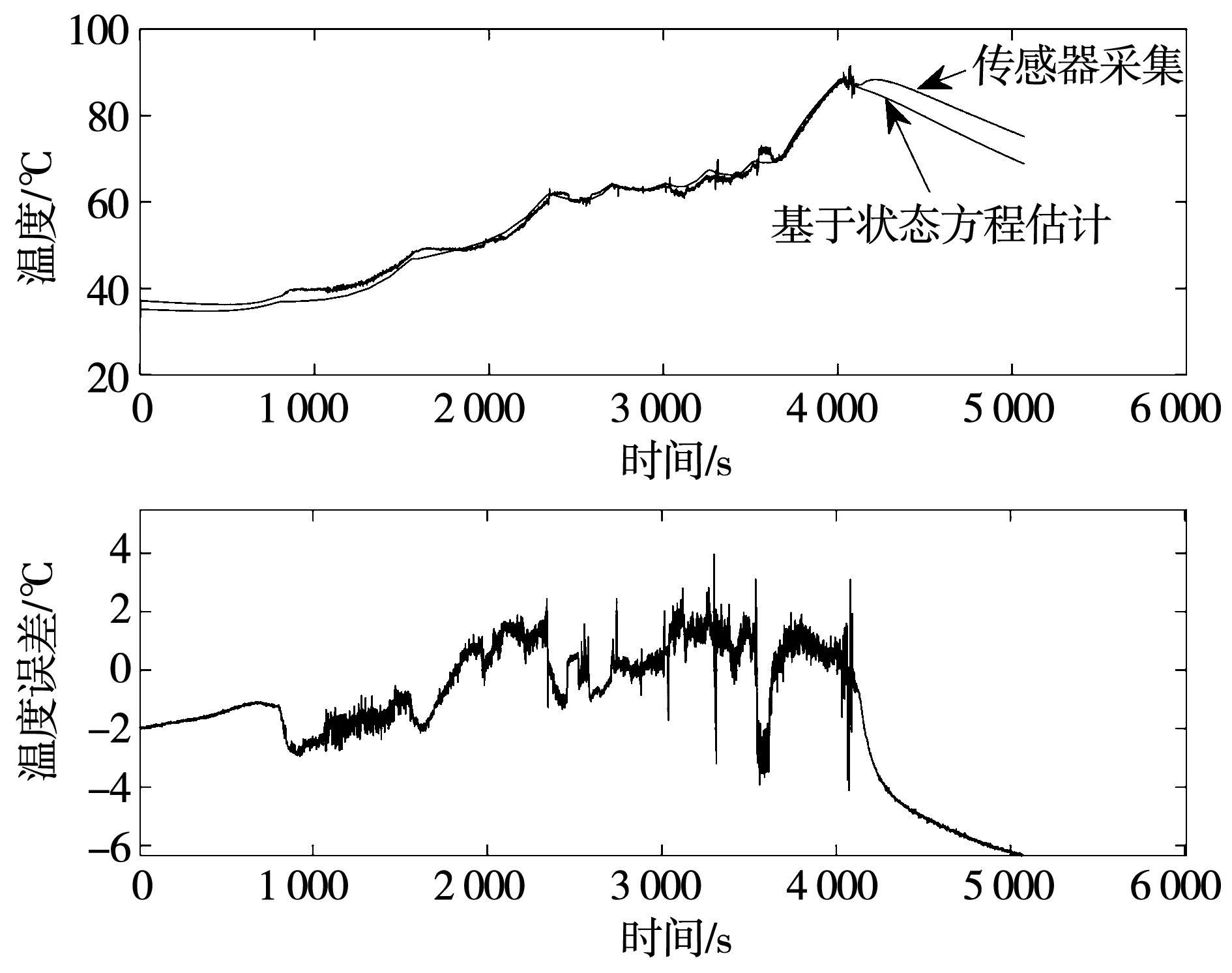
图12 混合实验工况下转子温度估计对比Fig.12 Comparison of rotor temperature estimation under mixed experimental conditions

转子温度估计误差产生的原因：基于等效铁损电阻计算的铁心损耗是对稳态情况下铁心损耗的近似，因此在工况剧烈变化的情况下，损耗估计结果可能会有较大的偏差，因此导致了在电机转速和转矩迅速下降之后的温度估计误差。但是在电机停机之后，由于没有了外部的能量输入，定转子温度将逐渐趋于一致，估计误差也会随着时间逐渐消除。

4 结 论

通过对基于传热学热模型的详细分析，本文提出了五节点集中参数热模型，并建立了相应的数学模型；提出了使用多元线性回归的方法对参数进行离线辨识并基于状态方程对电机转子温度进行在线估计。与现有的温度估计方法相比，特色主要体现在两个方面：热模型节点的选择和热模型参数的辨识。具体的总结如下：

1)本文所提出来的五节点集中参数热模型阶数较低，易于在电动汽车嵌入式系统中实现转子温度的在线估计。并且，模型通过适当的简化，能真实反映电机内部真实的热量流动。

2)本文提出了使用多元线性回归的方法对热模型参数进行辨识，该方法不依赖于电机的结构参数和材料的传热学特性。热模型中具体的参数不需要被估计，只需要对状态方程中的参数进行估计。该方式是用实际测量的温度对状态方程中的参数进行的拟合，能一定程度弥补热模型简化带来的温度估计偏差。

3)本文分别在堵转、低速和高速混合工况条件下基于状态方程对电机转子温度进行了预测，温度估计误差小于6℃。验证了所提出的热模型和温度估计算法的准确性。

在电机转子温度估计算法中，采用了专用的转子温度采集设备，用于电机热模型参数的离线辨识和温度估计算法的验证。由于该算法设备价格昂贵，在后续的研究中，将研究使用其他的方法对转子温度进行测量以降低该算法的使用门槛。