基于辅助惯性功率调节的虚拟同步发电机模糊控制策略

张赟宁， 蔡明磊， 向芳洲， 胡松林

(1.三峡大学 电气与新能源学院，湖北 宜昌 443002；2.三峡大学 智慧能源技术湖北省工程研究中心，湖北 宜昌 443002；3.南京邮电大学 先进技术研究院，南京 210023)

0 引 言

由于传统火力发电大量使用非可再生能源，导致非可再生能源的日益衰竭，新能源发电的利用率逐年增高，因此新能源并网的相关技术也得到了广泛的关注[1-3]。新能源通常利用基于电力电子技术的逆变器接入电网，电力电子设备响应速度快，但不能为系统提供惯性和阻尼，大量的新能源并入电网会大大削弱电力系统的惯性和阻尼[4]。低惯性系统在受到扰动后支撑能力差、频率调节能力和阻尼特性弱，致使频率稳定受到威胁[5]。此外，光伏和风力等发电方式出力具有波动性、随机性和不可控性等缺陷，会使得低惯性电力系统的运行环境变得更加恶劣[6]。

为了解决新能源并网的问题，学者们提出一种新型的逆变器控制算法，即虚拟同步发电机(virtual synchronous generator, VSG)技术[7-9]，该技术的主要思想是模拟同步发电机的一次调频和转子运动方程，使接口逆变器具有传统同步发电机应对扰动时的输出特性，有效提高了新能源渗透率较高的电力系统的惯性和阻尼水平。VSG使得采用接口逆变器并入电网的新能源呈现出友好特性，因此引起了众多学者的广泛关注。

文献[10]提出在重点关注逆变器的控制算法时，可以采用直流电压源来替代直流侧的分布式电源。文献[11-12]通过在VSG有功控制的前向通道串联微分补偿环节，加快了VSG的功率响应速度，增大了系统阻尼比，从而有效减小了动态过程中功率振荡，但其输出角频率的超调量变大。文献[13-16]提出自适应惯性策略，指出在频率恶化阶段应该采用大惯性抑制频率恶化，而在频率恢复阶段应该采用小惯性加快频率的恢复速度，自适应惯性策略有效减小了频率超调，加快了频率恢复速度。文献[17-19]提出将自适应惯性和阻尼相结合进一步改善了VSG的性能，但自适应策略忽略了虚拟参数调节与系统输出功率和频率性能存在矛盾的问题[11]。文献[20]引入了与VSG基本结构相独立的强化惯性环节，在控制上更加灵活，但并未考虑该环节引发的有功功率超调问题。

上述文献都采取了一定的策略改善了VSG的性能，但鲜有文献研究惯性功率对VSG性能的影响。本文通过分析惯性功率对VSG角频率的影响，提出一种辅助惯性功率调节策略，此策略在扰动过程中根据系统频率偏差和频率变化率不断调节惯性功率的输出水平，并将该策略与自适应参数调节策略进行比较，得出两种策略的对应关系；设计出精细化的调节规律，基于此规律设计模糊规则，利用模糊算法动态调节辅助惯性功率，减小VSG输出功率和频率超调量，加快频率恢复速度。此环节仅在扰动过程中作用，扰动结束后此环节自动失效，不影响系统的稳态有功功率输出。通过仿真验证了所提策略的可行性和优越性。

1 VSG有功控制原理及数学模型

VSG的控制拓扑结构如图1所示，光伏和储能设置为共直流母线型，为保证光伏的高能量利用率，前级的DC-DC变换器实施最大功率点跟踪(maxi-mum power point tracking,MPPT)，储能系统则以直流母线电压Udc为控制目标来维持前后级的功率平衡。Lf、rf、Cf、Rf分别是逆变器滤波电感、寄生电阻、滤波电容和电阻。Lg和Rg分别是VSG与电网并网时的线路电感和电阻。通过控制PCC(公共耦合点)的开通和关断可以实现孤岛和并网两种模式的转换，同时将电网等效为无穷大母线。VSG的基本运行过程为：能量管理层利用各类预测和计划信息给出有功、无功功率参考值Pref和Qref，同时结合功率测量装置得到的实时输出有功功率Pout和输出无功功率Qout；再通过VSG控制算法输出电压E和功角δ，进而经过电压、电流双环控制输出相应的信号，经过SPWM调制器生成脉冲信号来控制逆变器开关管的通断，完成整个控制过程，从而改变逆变器输出功率特性。

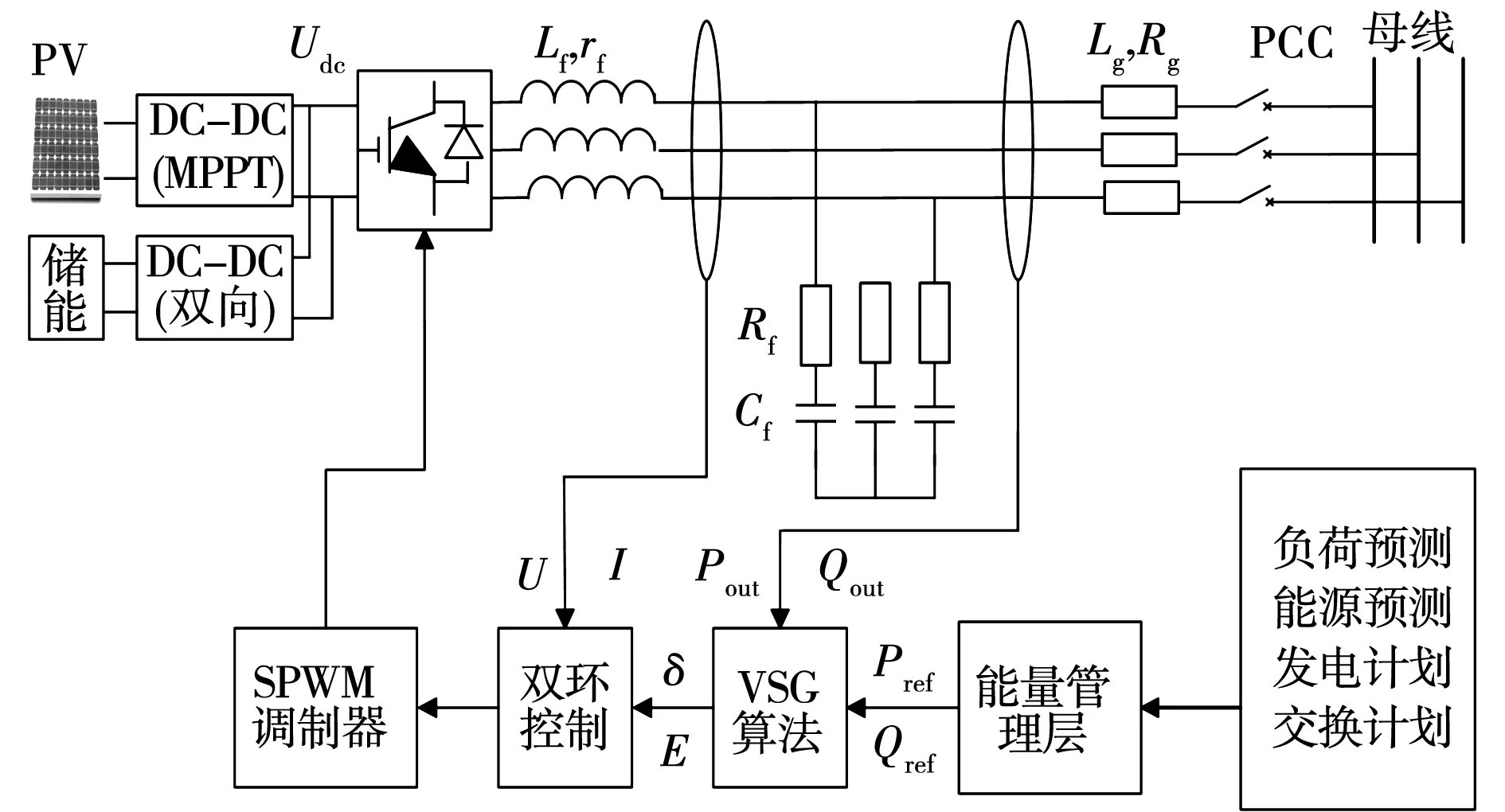
图1 VSG控制拓扑结构Fig.1 Topology of VSG control

采用电压源型VSG的建模方式，其核心在于将同步发电机的转子运动方程数学模型嵌入到逆变器的控制算法，使逆变器具有同步发电机的惯性和阻尼特性。转子运动方程为

(1)

式中：J和D分别为虚拟惯量和虚拟阻尼；Pm和Pout分别为虚拟机械功率和输出功率；ω0和ω分别为角频率参考值和输出角频率。

控制算法中还引入了同步发电机的调速器原理，即

Pm=Pref+Kω(ω0-ω)。

(2)

式中：Pref为有功功率参考值；Kω为虚拟调速器调差系数。

2 VSG有功控制性能分析

2.1 虚拟参数对有功控制的影响

结合同步发电机的转子运动方程和调速器的下垂方程，可以得到当功率不平衡时输出角频率的偏差与功率变化量的传递函数为

(3)

根据式(3)可知，该传递函数为一阶惯性环节，当系统的功率发生突变时，频率不会立即发生变化。

由式(1)、式(2)可以得到VSG有功-频率控制框图如图2所示。

图2中：ωg为电网电压角频率；δ为VSG输出电压与电网电压的相角差；Kp为δ至Pout的比例系数。

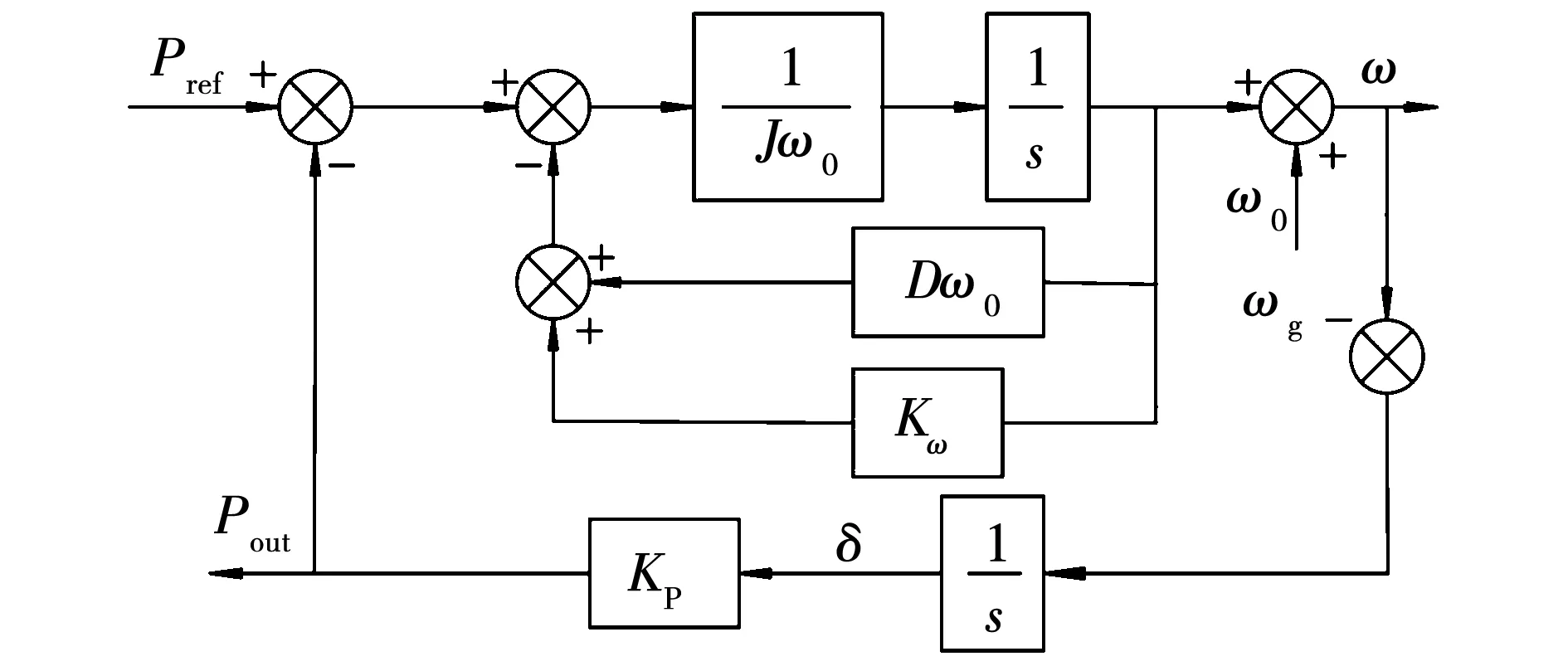
图2 VSG有功-频率控制框图Fig.2 Active power-frequency control block diagram of VSG

图3为VSG处于并网模式时的等效模型，E为逆变器输出电压，U为电网电压，Zfiflter为逆变器滤波阻抗，Zline为逆变器输出线路阻抗。将电网电压设为参考电位，记作U∠0，则逆变器的输出电压为E∠δ，电网频率为工频时，功角为

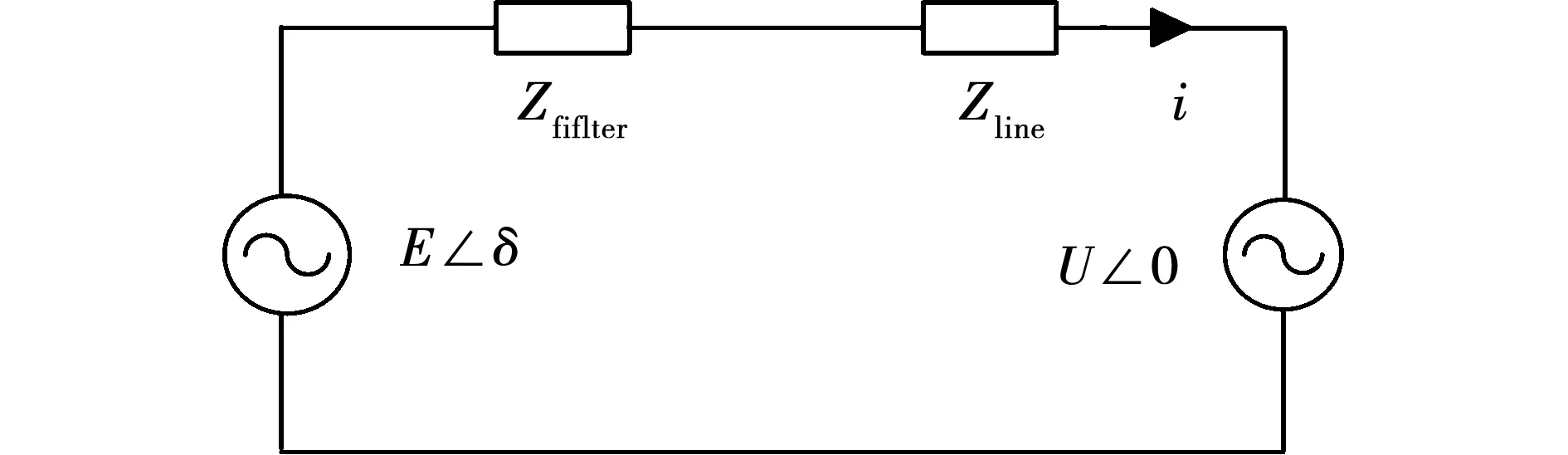
图3 VSG并网等效模型Fig.3 Equivalent model of grid-connected VSG

(4)

在稳态时，功角δ一般较小，此时有sinδ≈δ，输出功率为

(5)

将式(5)分别求一阶、二阶导数后可得：

(6)

将式(6)和式(2)代入式(1)中，可得

(7)

将式(7)拉式变换后整理可得VSG并网时的有功闭环传递函数为

(8)

选取不同的参数绘制出传递函数极点的变化趋势，箭头所指方向为D增大的方向，如图4所示。

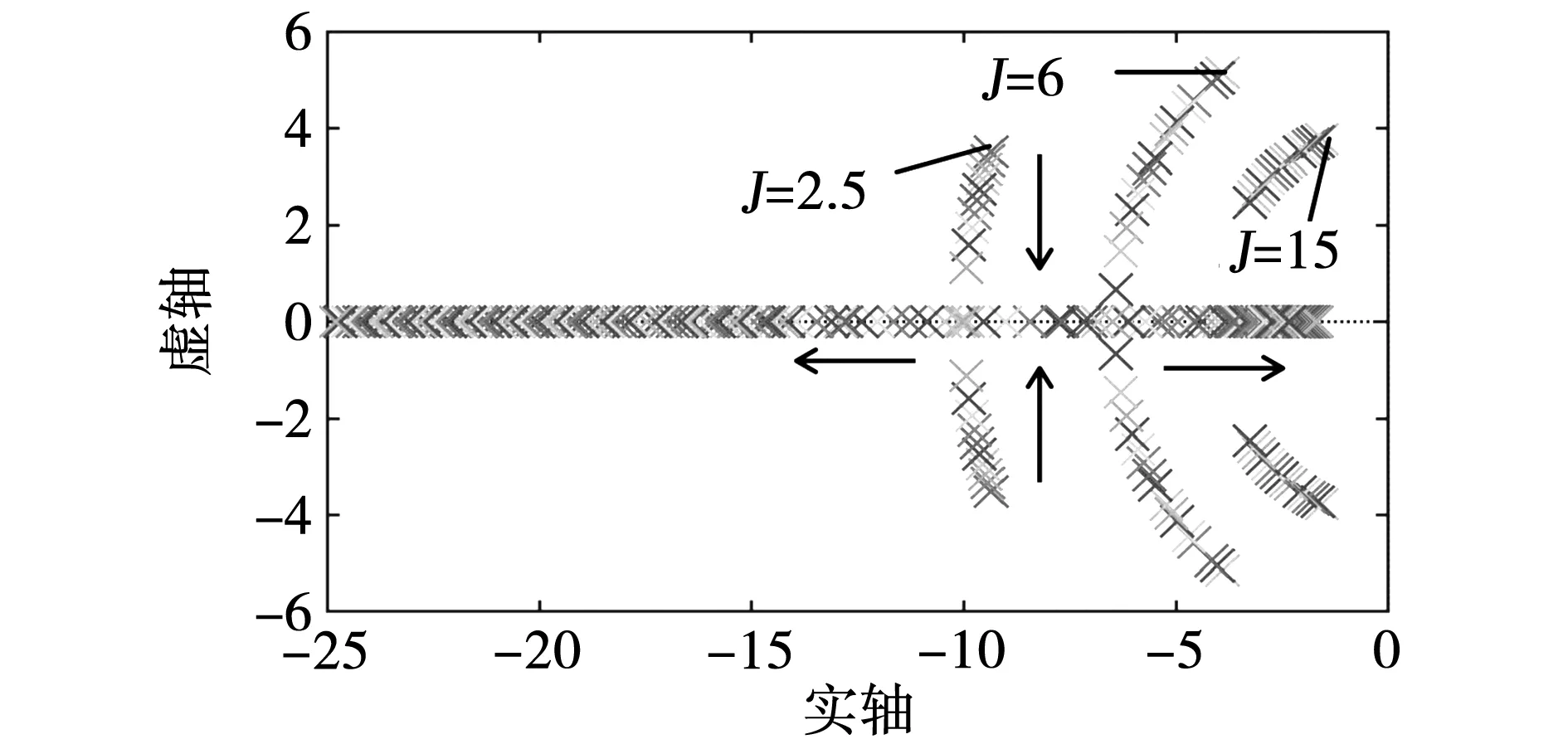
图4 VSG有功闭环零极点分布图Fig.4 Pole-zero map of active power loop of VSG

根据图4可知，当VSG的虚拟惯量J分别设置为2.5、6、15时，极点S1、S2的位置离虚轴越近，J的增大会使得VSG的稳定性变差。虚拟阻尼D不断增大后，极点的位置按照箭头所指方向移动，极点由共轭极点变为实数极点，系统从欠阻尼转变到过阻尼，VSG的响应速度变慢，根据文献[11]中的分析可知，增大D还会使输出有功功率稳态误差增大。而J和D较小，VSG抑制频率变化的性能较差，扰动过程中的最大角频率偏差值较大。基于上述分析可知虚拟参数的调节在优化系统的过程中存在矛盾。

2.2 惯性功率对角频率的影响

传统同步发电机在正常运行时保持同步转速，此时电网角频率维持在100π，当系统遭遇功率扰动后，功率平衡状态被打破导致系统角频率发生变化，由于发电机转子具有较大的质量，当其高速旋转时产生的巨大惯性能够减缓角速度变化速度，在频率变化过程中转子动能的变化会引起吸收和释放电磁功率，VSG正是模拟发电机转子在这一动态过程中的能量变化过程来为系统提供惯性功率支撑。

根据文献[21]惯性功率表达式为

(9)

式中：ω0为额定角频率，虚拟惯量J为定值时，惯性功率与角频率变化率相反值成正比关系，且转子加速运动时吸收功率，其符号为负；转子减速运动时输出功率，其符号为正。虚拟惯量J和角频率变化率的幅值决定了惯性功率的大小。指令功率发生阶跃时惯性功率和角频率曲线如图5所示。

当系统的指令功率发生阶跃变化时，会使得角频率上升，VSG控制策略能够利用储能来模拟转子吸收能量，在短时内为系统提供频率支撑。此策略存在的缺点是：由于模拟了转子运动的全过程，在转子转速到达峰值后至恢复为额定值，此过程做减速运动释放能量，因而储能系统也会释放能量(图5中的阴影部分)。实际上，此阶段系统的角频率还未恢复稳定，储能系统释放的能量会使得系统输出功率增大，对系统频率上升产生“叠加效应”，使系统角频率偏差变大，导致系统的频率响应特性变差，储能不合时宜的动作使得输出功率出现超调振荡现象，容易触发VSG的反向电流保护。

图5 惯性功率对角频率的影响Fig.5 Influence of inertial power on angular frequency

3 基于辅助惯性功率调节的VSG控制策略

根据第2节的分析，VSG模拟的惯性功率受频率变化率符号的影响，会对其性能产生负面影响。而VSG的惯性功率由储能系统提供，可以通过控制作用改变其出力规律，从而避免上述不利影响。

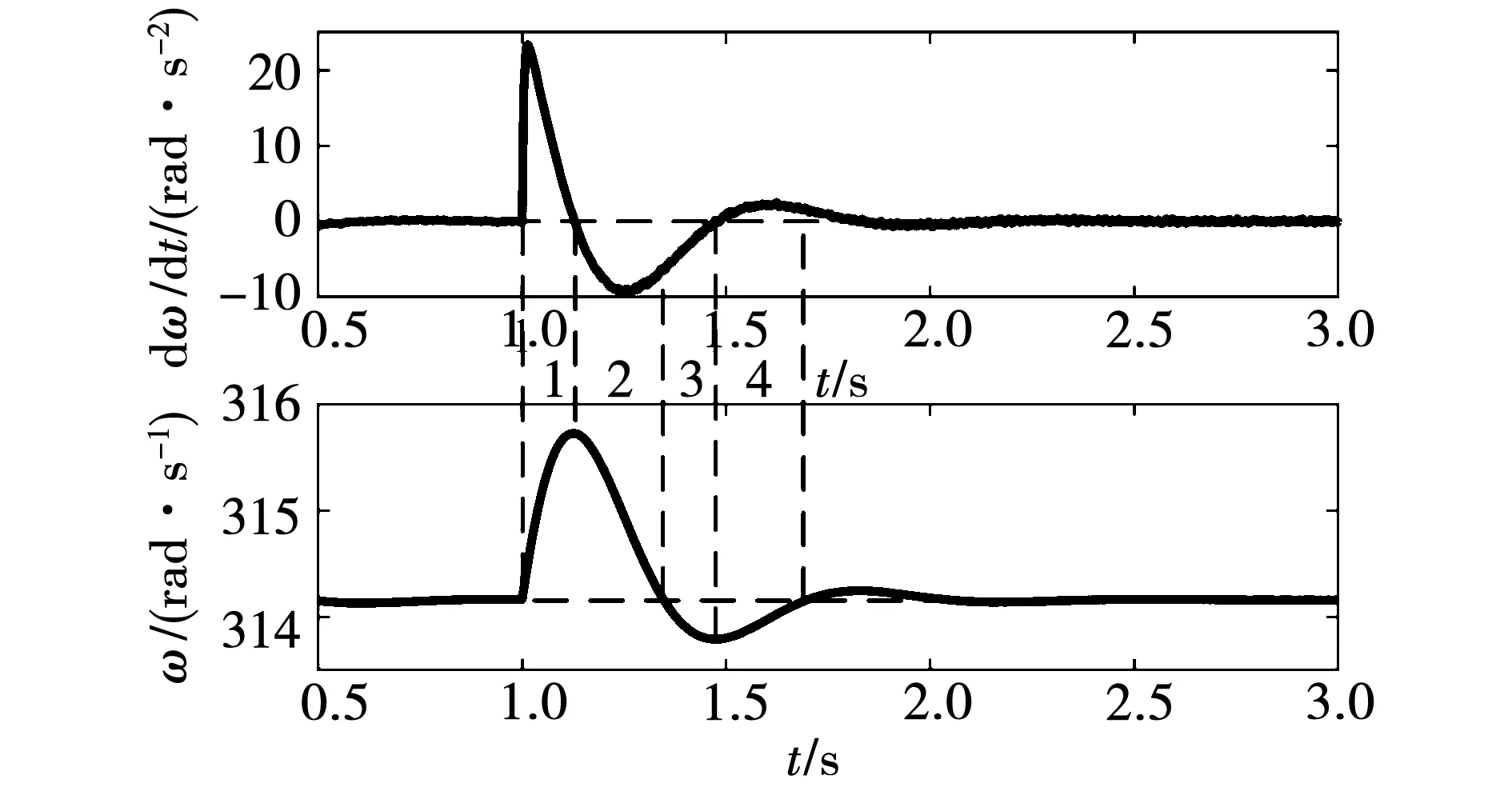
图6 频率偏差和频率变化率区间划分Fig.6 Interval division of frequency and frequency change rate

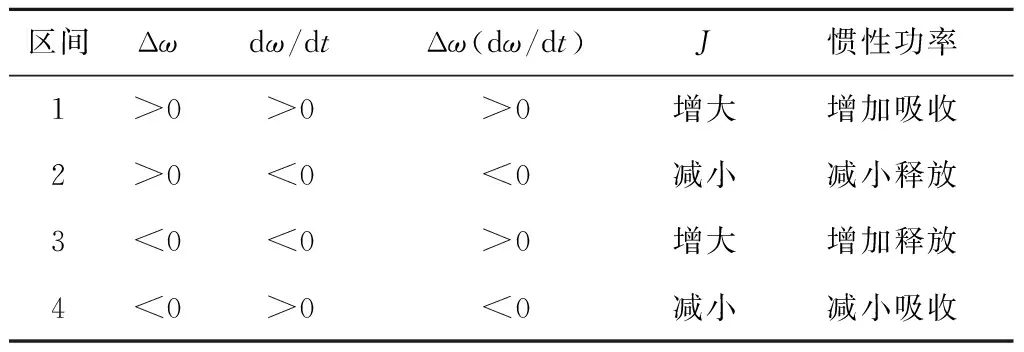
表1 文献[14]不同区间虚拟惯性和惯性功率对应关系

3.1 普通型惯性功率调节

在VSG的基础结构上增加辅助惯性功率Pad，同时此环节定义为普通型惯性功率调节，引入的辅助惯性功率Pad能够根据频率变化率和频率偏差自适应调节，其表达式为：

(10)

式中r为惯性功率调节阈值，设置阈值以避免频率轻微波动造成的辅助惯性功率环节频繁动作。根据第2节分析，将dω/dt取绝对值是为了使Pad调节不受频率变化率符号的影响，根据文献[22]可知下垂控制能够让储能出力与系统角频率恢复稳定的需求出力方向一致，于是利用Δω判断Pad调节方向，确保调节利于频率稳定。K为调节补偿系数，该系数的设置需要确保惯性功率调节值不大于最大功率波动值ΔPmax，否则将对系统产生负作用，具体设置将在第4节说明。

在保留传统VSG基本结构的基础上，增加辅助惯性功率调节的改进VSG有功控制如图7所示。

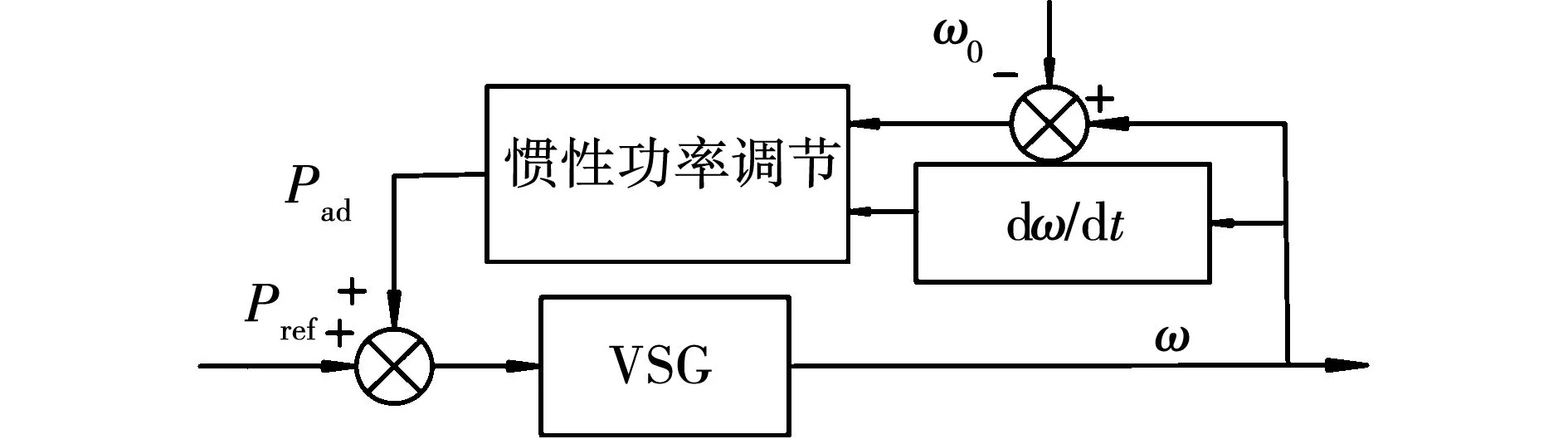
图7 改进VSG有功控制Fig.7 Active power control of improved VSG

根据图7，可得改进后的VSG动态方程为

(11)

式中KD=Kω+Dω0，当频率变化率大于调节阈值r时，将式(10)代入式(11)可得

(12)

将表1中Δω和dω/dt的符号代入式(12)等号左侧，并将各变量取绝对值，符号提取至前方可得：

随着临床工作对抗血小板治疗的重视，患者在服用强效抑制血小板聚集的药物的同时其出血风险也相应地增加。GRACE、HORIZONS-AMI、ACUITY等研究结果显示研究ACS患者院内30天出血发生率高达3.0%～8.3%[22-24]。 而中国的ACS临床路径的疾病登记研究结果也证实ACS患者院内大出血风险接近5%[25]。患者的高出血风险往往预示着其临床预后较差，其死亡率可显著升高。研究结果显示，ACS患者若在住院期间发生大出血，其死亡风险可升高3倍～6倍[26]。

(13)

由式(1)、式(2)、式(12)和式(13)可知，增加的惯性功率调节项等效于在动态过程中改变虚拟惯量的大小，相比于自适应参数J调节策略，辅助环节与传统VSG结构相对独立，在控制上更加灵活，能够避免参数调节带来的矛盾。

3.2 模糊控制惯性功率调节

根据上节的分析已基本明确了动态过程中惯性功率的调整原则，为了进一步提高控制的精度，将表1中各个区间进行更加细致的划分，得出的惯性调节功率的控制规律如表2所示，同时利用所得规律设计模糊控制器如图8。K1和K2为输入量化因子，K3为输出量化因子。增加了模糊惯性功率调节环节后新的惯性功率表达式为

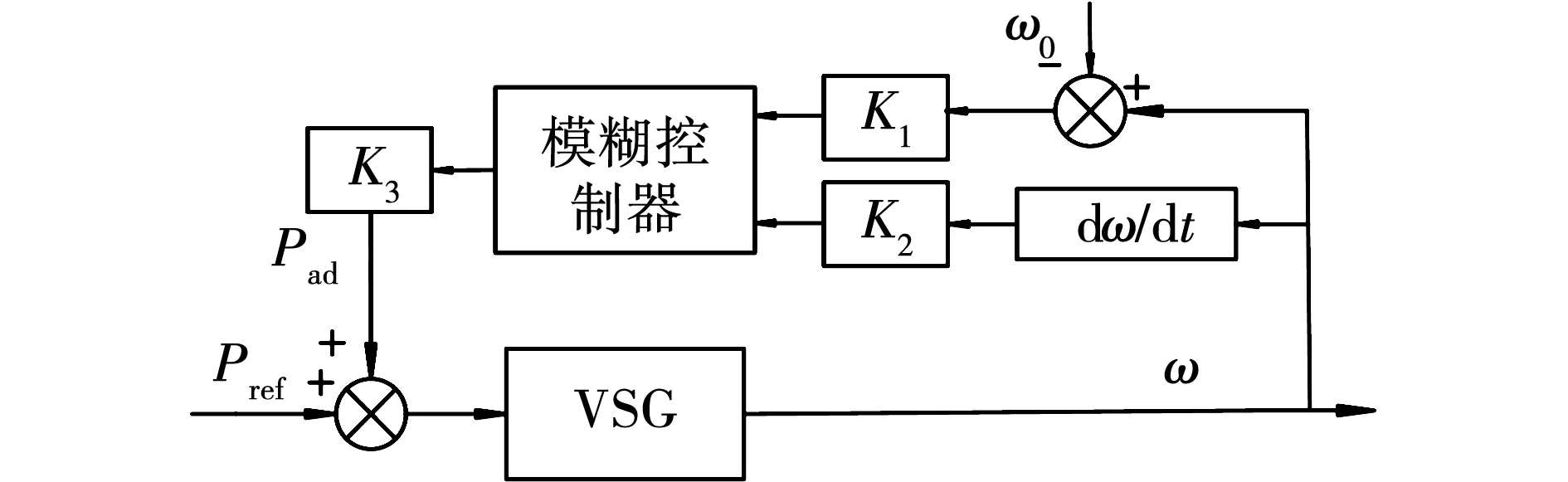
图8 采用模糊控制的惯性功率调节Fig.8 Inertial power regulation with fuzzy control

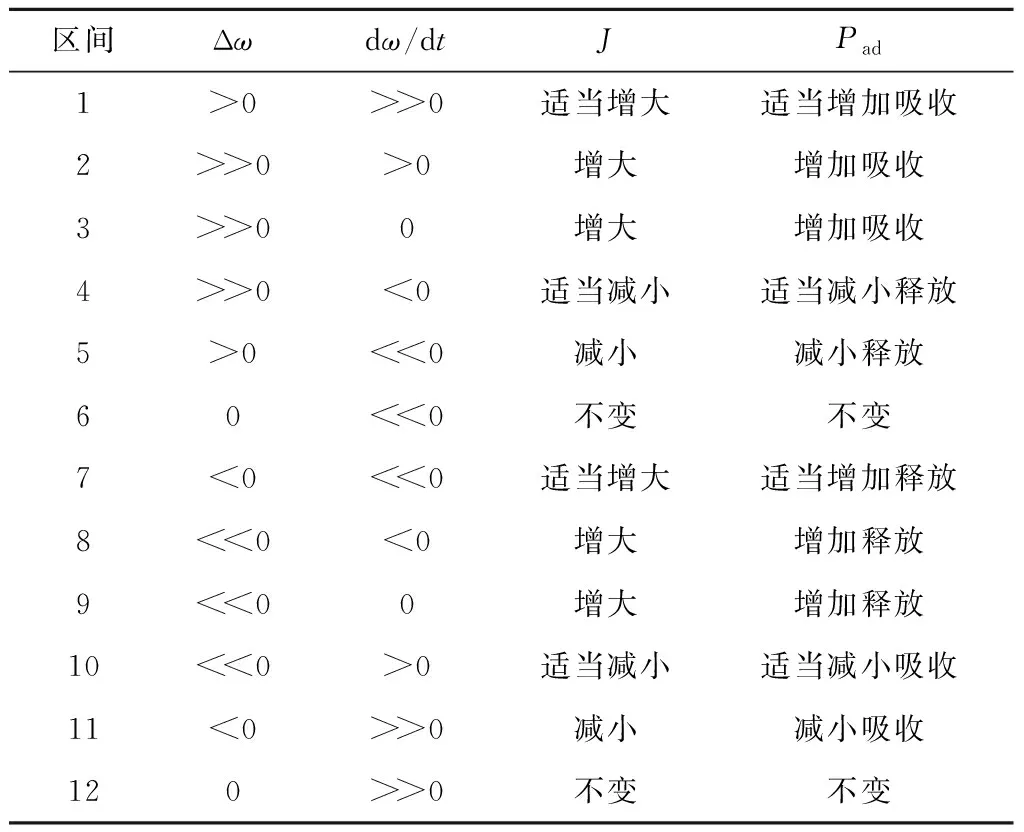
表2 惯性功率调节的模糊控制规律

(14)

根据式(9)，Pad的符号设置逻辑为：若吸收功率其为负值，若释放功率则其为正值。

模糊控制器的设计包含：模糊化、模糊推理、反模糊化。接下来分别予以说明。

模糊化：利用量化因子将频率偏差和频率变化率这两个输入变量做归一化处理，K1和K2分别为最大功率波动下的角频率偏差和角频率变化率幅值，则角频率偏差和角频率变化率的基本论域设置为[-1，1]。将输出变量的变化范围也设置为[-1，1]，代表惯性功率调节比例U，同上一小节，K3的范围可根据最大功率波动ΔPmax设置为[0，ΔPmax]，具体设置将在第4节说明。通过定义隶属度函数可将输入输出转化为模糊变量，主要使用三角形和S型隶度属函数，并将量化后的输入、输出划分为5个等级：NL(负大)、NS(负小)、ZO、(零)、PS(正小)、PL(正大)。得出输入和输出的隶属度函数如图9所示。

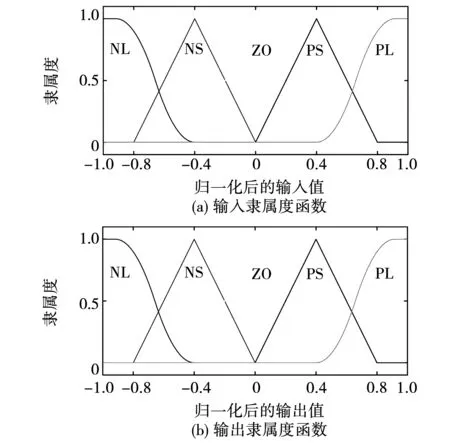
图9 输入和输出的隶属度函数Fig.9 Membership functions for input and output

模糊推理：根据表2总结的控制规律，同时结合输入和输出隶属度函数，设计的基于Mamdani型的模糊规则如表3所示。

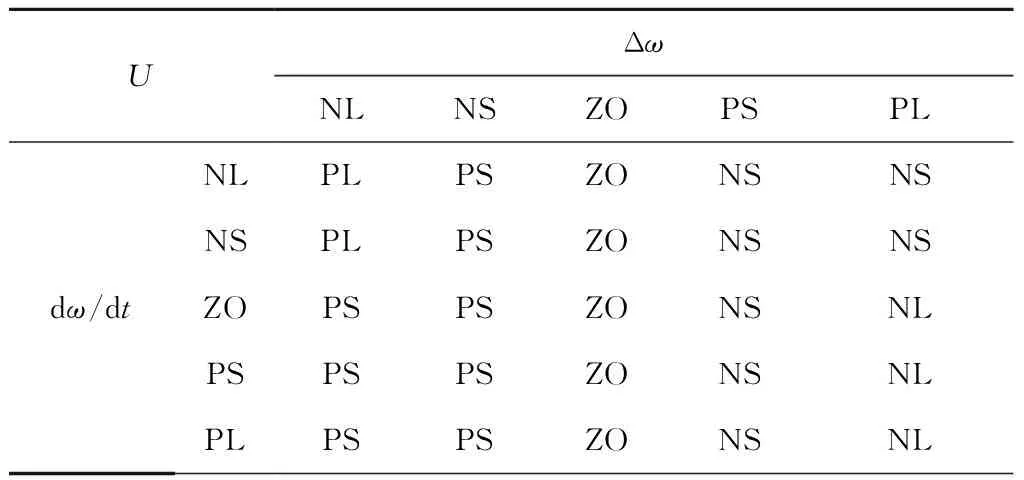
表3 惯性功率调节的模糊规则

反模糊化：使用重心法对输出进行反模糊化处理，最终得到惯性调节功率比例。得到的系统的输出结果如图10所示。

图10 模糊逻辑推理结果Fig.10 Fuzzy logic inference results

4 仿真分析

为了验证所提辅助惯性功率调节策略的有效性，利用MATLAB/Simulink仿真平台搭建了如图1所示的仿真模型。考虑储能系统能够满足功率需求，仿真中将直流侧的光伏和储能系统用直流电压源代替。其主要仿真参数如表4所示。

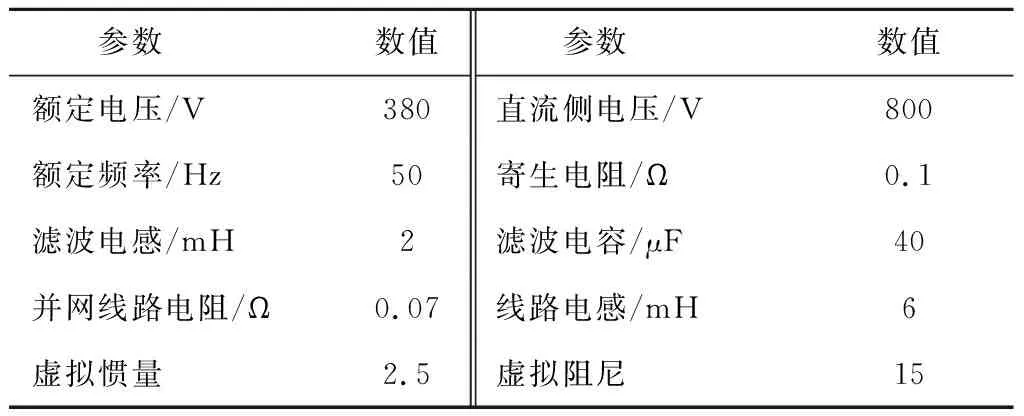
表4 仿真参数

首先，在仿真中设置有功功率指令Pref=0，并设置在1 s时突变为Pref=20 kW。图11和图12分别给出了普通型和模糊控制辅助惯性调节策略下各参数设置和VSG性能的关系。在最大功率波动ΔPmax的约束下，若K和K3设置的过小，则有功功率超调和频率偏差的优化效果稍差，但2个参数的值设置的过大时，虽然有功功率超调量和频率偏差更小，可系统的调节时间变得更长，并且普通型惯性功率调节策略的角频率出现振荡现象。综合考虑，K和K3可适中选取。

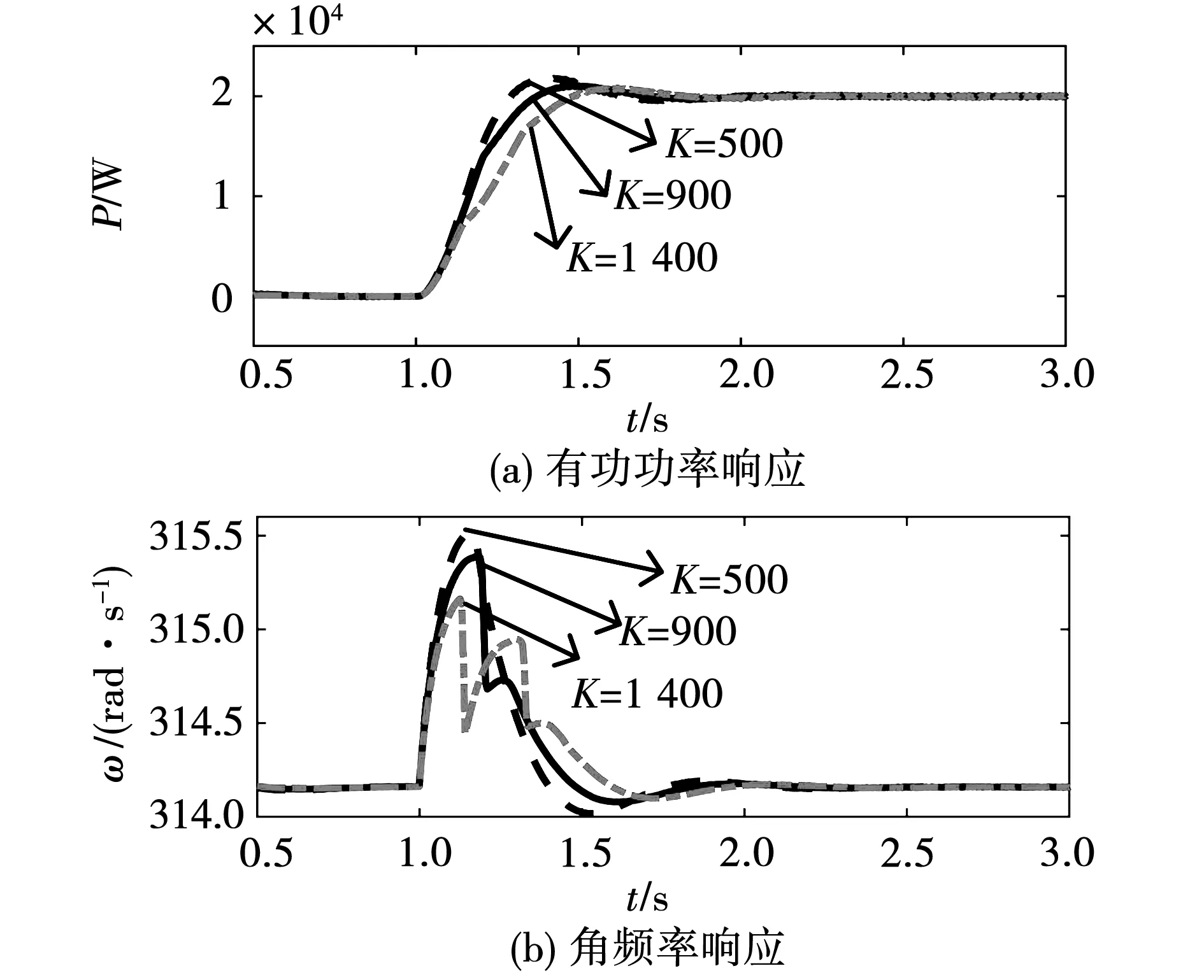
图11 普通型调节系统响应Fig.11 Response with general regulation

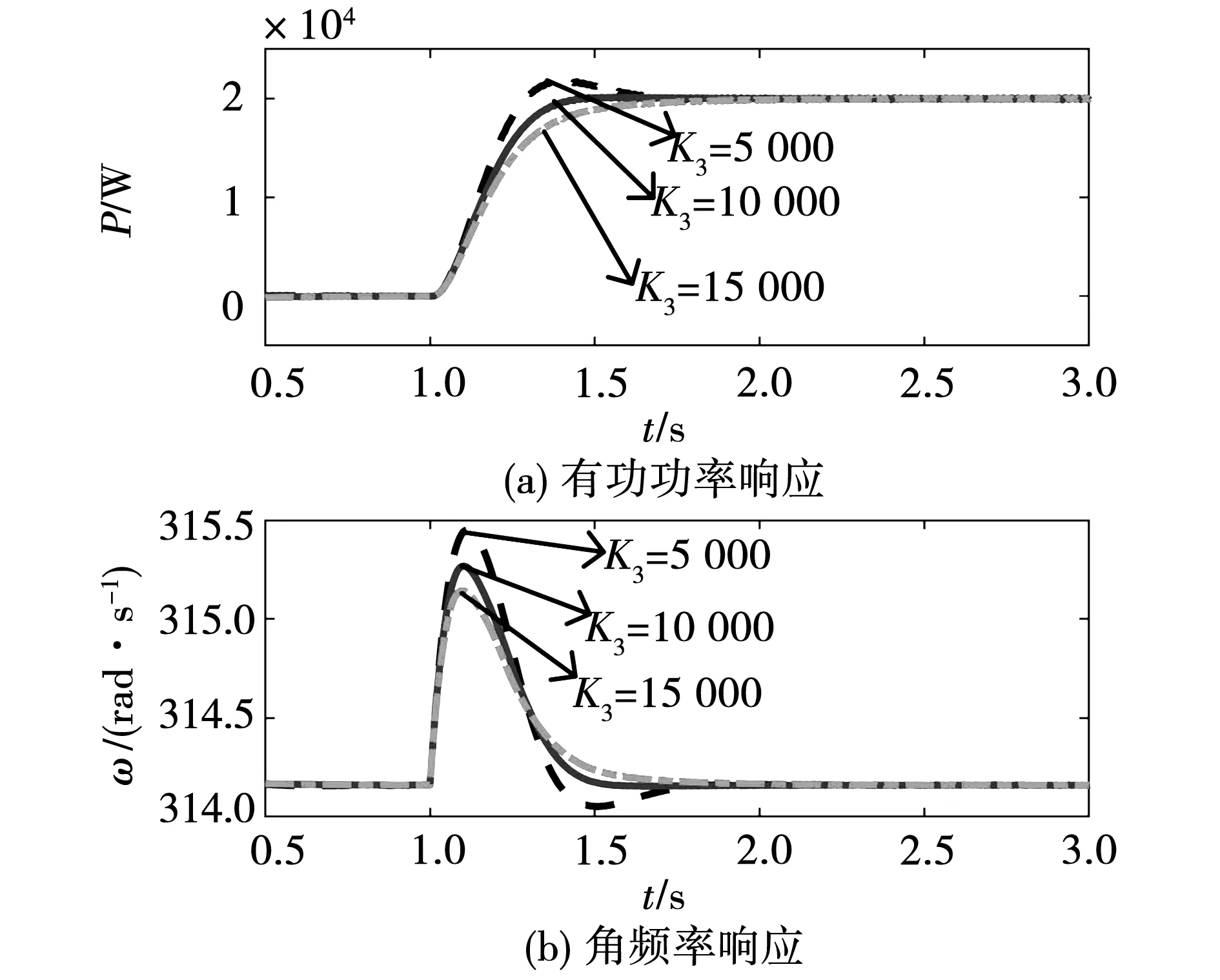
图12 模糊控制系统响应Fig.12 Response with fuzzy control

设置工况1有功功率指令Pref在1 s时突升为20 kW和工况2有功功率指令Pref在3 s时突降为10 kW。分别采用传统VSG策略、自适应虚拟参数J调节策略(J的调节规律如表1)、普通型惯性功率调节策略和模糊控制惯性功率调节策略。得出采用各种策略时有功功率和角频率响应如图13所示。

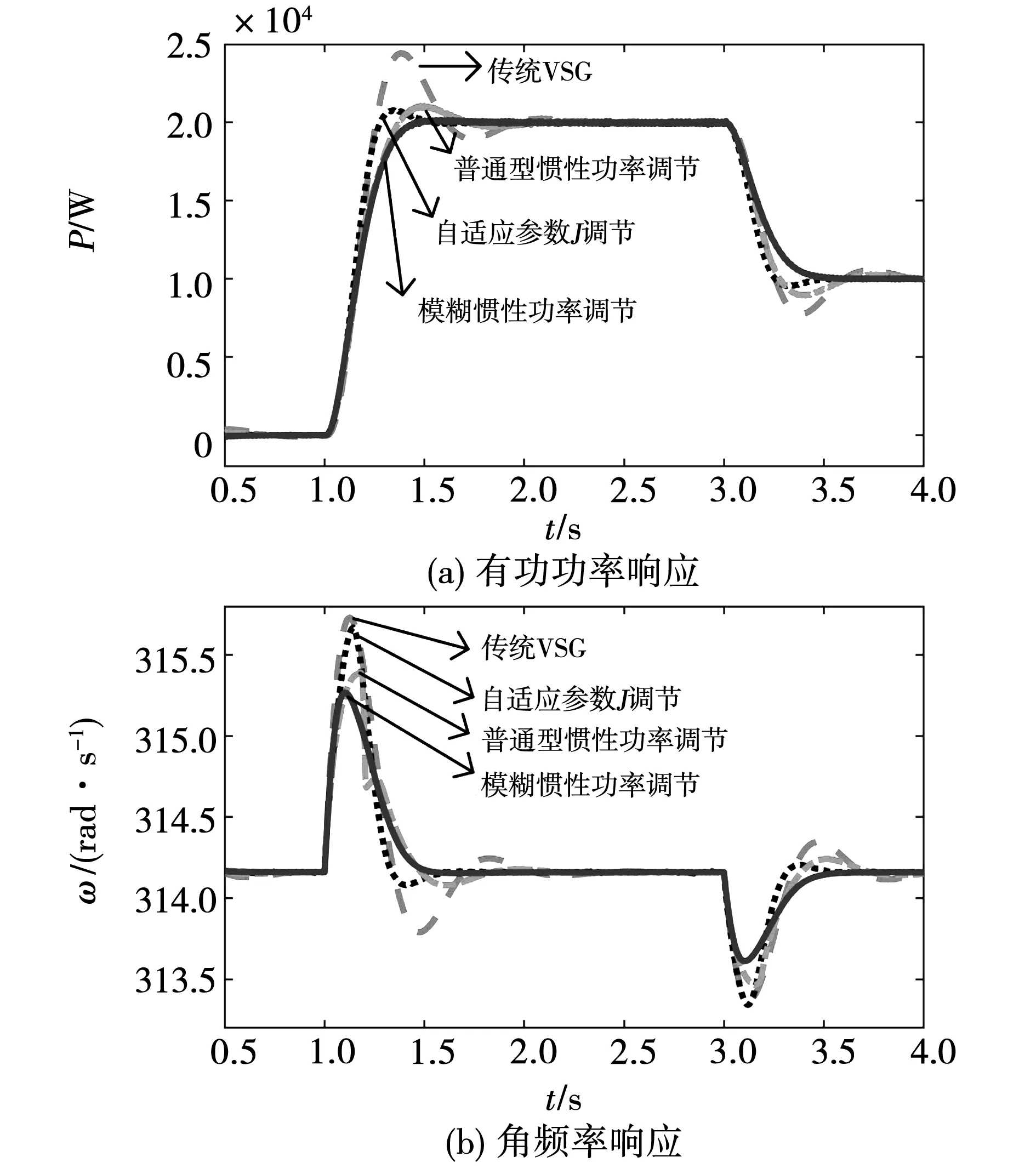
图13 连续功率指令扰动的响应波形Fig.13 Response under continuous power instruction disturbance

从图13可以看出，采用各种改进策略后，VSG在连续扰动工况下的有功功率和角频率响应特性均得到了改善。具体分析工况1：采用传统VSG策略时，有功功率超调量和调节时间分别为21.6%和1.21 s，角频率最大偏差和调节时间分为1.54 rad/s和1.34 s；采用自适应虚拟参数J策略时，有功功率超调量和调节时间分别为3.75%和0.54 s，角频率最大偏差和调节时间分为1.44 rad/s和0.59 s；采用普通惯性功率调节时，有功功率超调量和调节时间分别为5.3%和0.99 s，角频率最大偏差和调节时间分为1.24 rad/s和1.10 s；采用模糊控制惯性功率调节策略时，有功功率超调量和调节时间分别为0.65%和0.50 s，角频率最大偏差和调节时间分为1.14 rad/s和0.52 s。仿真结果显示，采用模糊惯性功率调节策略的VSG各性能均优于传统VSG和另外两种改进策略。

5 结 论

针对虚拟同步发电机技术引发的功率振荡，且通过调整自身参数无法很好的兼顾有功功率和角频率响应特性这一问题，本文引入辅助惯性功率调节策略，与自适应参数J调节策略进行了对比分析，总结出更加细化的惯性功率调节规律，并利用模糊算法实现惯性功率的调节。改进后的模糊惯性功率调节策略有效减小了功率超调量和角频率最大偏差，同时缩短了系统的调节时间。对于调节补偿系数和输出量化因子的设置，实际还需要考虑储能荷电状态动态调整，这将是本文后续的研究内容。