主动磁悬浮轴承的滑模自抗扰解耦控制

李冰林， 曾励， 张鹏铭， 竺志大

(1.南京林业大学 汽车与交通工程学院，南京 210037；2. 扬州大学 机械工程学院，江苏 扬州 225009；3.浙江精功科技股份有限公司，浙江 绍兴 312030)

0 引 言

气流纺中，纺杯的转速与纺纱的效率和质量戚戚相关，转速越高，生产效率越高。抽气式转杯转速可达13万～15万r/min。采用磁悬浮轴承技术的新型高速纺杯，可以大大减小功耗，降低噪声，与传统的机械轴承相比，具有明显的优势[1]。在开发这种高速转杯纺纱机时，应解决磁轴承的控制稳定性问题。

根据转子动力学理论，五自由度的磁悬浮轴承，轴向和径向之间的耦合作用小，可忽略，对轴向单独进行控制即可，于径向而言，4个自由度之间存在着非线性、强耦合，需对其进行解耦才能获得较好的控制性能[2]。文献[3-4]采用的方法是对系统进行强制解耦，然后再采用分散的独立控制，这种解耦控制方法会使系统模型产生一定的误差，同时会忽略转子高速时产生的陀螺效应，这样的控制方法往往难以满足需求，特别是在纺纱转杯的高速控制应用上。一种传统的方法是通过设计解耦补偿器，使其与磁悬浮对象模型组成的广义矩阵，再使其对角化，从而使耦合的系统解耦[5]。文献[6-7]采用前馈解耦内模控制的方法，实现径向偏转解耦控制。郑世强[8]等采用交叉反馈的相位裕度跟踪补偿控制的方法，实现全转速范围内的章动模态稳定性控制。以上这些解耦方法对控制对象的数学模型要求很高，当系统控制过程中包含很多非线性、时变的多变量后，很难满足控制需求。针对磁悬浮转子存在陀螺效应的影响，沈易霏[9]等一种针对非对称转子的转速自适应的多通道单边滤波PIDC控制方法，在不同的转速段内自动切换反馈通道，通过优化预调参数对转子远离质心一端出现的涡动模态失稳的现象进行相位补偿。陈亮亮[10]采用逆系统求解的方式很好地实现了对系统的解耦，但该方法需满足对求解方程的可逆性。智能解耦在解决系统非线性问题有其优势，如神经网络系统具有自学习、自适应能力，但它需要和其它算法相结合来满足解耦控制[11-12]。同时，这种智能解耦的方式需要预先对样本训练，计算量大。

自抗扰控制(active disturbance rejection control,ADRC)在非线性、时变、系统耦合的情况下能获得良好的控制性能，在电机抗扰动控制、旋翼姿态控制等都要较好的应用[13-16]。非线性控制中，滑模控制具有响应快，对参数变化不敏感，控制易于实现等优点，同时结合其它先进的控制理论，能实现对参数不确定性或时变系统的控制[17-18]。

论文针对磁悬浮电机轴承系统，结合滑模控制和自抗扰控制的优点，对系统存在的自由度耦合和陀螺效应耦合进行解耦控制。当系统存在外界扰动时，采用扩张状态观测器(extended state observer, ESO)能对这种扰动进行有效估计，并进行控制补偿，以提高系统抗干扰能力。为了进一步提高控制的性能，再对传统的ADRC算法进行改进，设计一种基于滑模变结构的自抗扰控制器，提高系统的控制效果。

1 系统模型和问题描述

1.1 系统模型

图1为主动磁悬浮轴承控制系统工作原理图，系统工作在平衡工作点(i0,x0)附近，f是2个电磁铁的电磁力，i0是2个线圈中的偏置电流。当系统工作时，转子受到扰动，并从平衡位置x0向下偏移，转子距预设平衡位置的距离经传感器检测，得出的偏差输入到控制器中。控制器紧接着输出控制信号，然后经功率放大器放大处理后向两个磁极线圈中输入电流，分别为i0+ij和i0-ij，在两者产生的电磁力的共同作用下，将转子拉回到平衡位置。针对单一电磁铁作用，电磁力可以表示为

图1 主动磁悬浮轴承系统工作原理图Fig.1 Schematic diagram of active magnetic bearing system

(1)

其中：K=μ0n2S0/4；μ0为真空磁导率；n为线圈匝数；S0为极横截面积；x为转子位置，电流i增加，电磁力增加，间隙x增加，电磁力减小。

对于图1中这种U型磁极，两个磁极作用在转子上的力都带有角度α，考虑α作用，则有[19]

(2)

由于系统采用差动方式驱动，一个电磁铁由i0+ij电流驱动，另一个由i0-ij电流驱动，如图1所示，所以电磁线圈对转子可以产生正向和反向作用力。在式(2)中，用i0+ij和i0-ij代替i，同样气隙用x0-xj和x0+xj代替x，可以得到该自由度的电磁力为

(3)

式中：ij、xj分别是第j自由度处的控制电流和转子位移；x0为给定气隙。每个自由度的电磁力与电流和气隙的平方值相关，在平衡点进行泰勒级数展开，略去高次项，可以统一表示的形式为

Fj=Kxjxj+Kijij，j=1,…,5。

(4)

式中Kij,Kxj分别为第j自由度上电流-力刚度和位移-力刚度。图2是磁悬浮轴系统转子的受力示意图。忽略轴向和径向间的耦合，径向传感器的布置和轴承线圈在同一个平面上。

图2 五自由度主动磁悬浮轴承系统结构图Fig.2 Structure of 5-DOF AMB rotor system

由转子动力学得如下方程为：

(5)

式中：m为转子质量；Fuv表示转子在v端u轴方向的受力(v=a,b；u=x,y)；Fzc为转子在Z轴方向上的受力；xc、yc、zc分别为转子在质心处X轴、Y轴、Z轴方向的位移；θx、θy分别为转子绕质心处X、Y轴的转角；ω为转子绕Z轴的转动角速度；la和lb分别为质心到两侧轴承端的间距；Jy和Jx分别是转子绕质心处Y轴和X轴的转动惯量，其中xc、yc和θx、θy可以由xa、xb、ya、yb替代，可得：

(6)

式中：xa为转子在a端X轴方向的位移；xb为转子在b端X轴方向的位移；ya为转子在a端Y轴方向的位移；yb为转子在b端Y轴方向的位移。系统中假设电磁线圈对称布置，每对线圈特性相同，所以其在径向的位移-力刚度Kxr和径向电流-力刚度Kir一致，根据式(4)可知：

(7)

式中：ixa、ixb分别为a、b端X轴方向电磁铁的电流；iya、iyb分别为a、b端Y轴方向电磁铁的电流；izc转子轴向电磁铁的电流；Kxz、Kiz分别为轴向的位移-力刚度和轴向电流-力刚度。

结合式(5)～式(7)，得到系统的状态方程为：

(8)

1.2 问题描述

在实际工作过程中，电磁线圈存在着漏磁现象，铁心具有磁阻，存在着磁饱和问题等因素，会使系统的不确定性增加，同时外界的环境包括振动对系统控制都有一定的影响。同时由式(8)可知：

1)磁悬浮轴承在径向存在着耦合，在X方向，xa、xb存在着耦合，在Y方向，ya、yb存在着耦合。

2)由于a22中存在±laJzω/lJy项，表明其值受转子转速ω的影响。这说明X、Y两个方向都有陀螺效应耦合，在低转速时，laJzω/lJy≈0,可忽略，但在高转速，特别是纺杯的转速高达200 000 r/min，该陀螺效应不应该被忽略。

因此，针对上述问题，首先必须对系统存在的径向位置耦合进行解耦，然后设计一个具有良好抗外界干扰的鲁棒控制器，同时该控制器针对转子高速旋转时存在的陀螺效应耦合不具有敏感性。

2 自抗扰解耦控制器

自抗扰控制有很好的鲁棒和动态特性，可以对系统运行时的内外扰动进行实时观测估计并进行补偿[20]。该控制方法不要求被控对象的精确模型和扰动模型。磁轴承转子在运行中由于存在磁场作用力的非线性，机械振动等不确定因素，使得依赖于模型的控制方法受到局限。采用自抗扰控制器对这些不确定因素进行动态估计和补偿能使系统能快速跟踪给定的目标值。

将矩阵(8)的形式写成含有状态变量的形式：

(9)

(10)

式中：

为各项内外扰动的总和，采用扩张状态观测器(ESO)估计出系统的扰动总和。因此，式(8)可看成是4个独立的二阶系统，可以单独设计自抗扰控制器。这样一个MIMO系统就转化为了相互独立的SISO系统，然后分别对其控制。ADRC控制器由跟踪微分器(TD)、ESO和非线性误差反馈器(NLEF)组成[21]。

下面以xa为例，详细说明磁悬浮轴承解耦抗干扰控制，主要包括3个部分。

2.1 跟踪微分器TD

目前离散式的跟踪微分器实现过渡过程比较应用普遍，其表达式为[14]：

(11)

式中：r为速度因子，其数值影响到v1跟踪到v的速度；v2为v1广义导数；h0为滤波因子，加大其数值，可以使得噪声污染程度减小；fhan(v1,v2,r,h0)为最速控制综合函数。

2.2 线性扩张状态观测器

对于具有一个自由度的二阶非线性系统，式(9)中各自由度可以表示为：

(12)

(13)

|sI-A|=s3+β01s2+β02s+β03=(s+w0)3。

(14)

2.3 非线性误差反馈律

基于TD输出的跟踪信号的输出v1，v2与ESO的估计值z11，z12的差值，构造系统误差和误差微分信号：

传统的非线性反馈控制的控制增益为

(15)

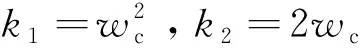
扰动反馈控制律为

u=(u0-z13)/b0。

(16)

此时系统变为双积分系统。

3 滑模自抗扰控制律设计

由传统的ADRC中非线性误差反馈控制律采用非线性函数，控制参数较多，而且缺乏具体的物理意义，整定费时费力。滑模变结构控制使得系统结构能根据其状态实时改变，其控制器设计包括滑模面和控制律的设计。论文将滑模变结构控制和自抗扰技术相结合，将自抗扰技术的非线性控制律设计改为滑模切换律控制，使得系统同时具有ADRC的抗扰能力，又具有滑模控制的快速响应特性。

3.1 控制律的设计

定义系统误差方程为：

(17)

(18)

式中的c满足Hurwitz多项式。采用滑模变结构对系统进行控制，会产生高频抖振问题。而指数趋近律能缩短趋近时间，使运动达到滑模面时的速度很小，能系统的抖振的影响。因此，选取指数趋近律为

(19)

其中ε>0，k>0，为选取参数。由式(18)得出滑模控制率为

mx11xa+εsgn(s)+ks]。

(20)

3.2 控制器稳定性分析

线性扩张状态观测器和滑模控制器构成的系统，其跟踪误差需是有界稳定的。根据选取的滑模面，取Lyapunov函数为

V=s2/2。

(21)

对其进行微分

(22)

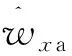
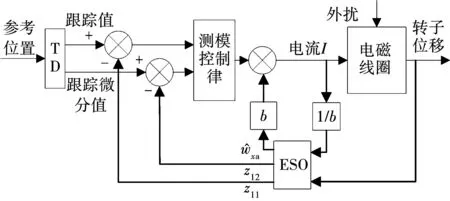
图3 单自由度滑模自抗扰控制框图Fig.3 Block diagram of 1-DOF sliding mode active disturbance rejection control

根据式(10)，由四自由度的磁悬浮轴承控制解耦结构图如图4所示。

图4 四自由度磁轴承滑模自抗扰解耦控制框图Fig.4 Block diagram of sliding mode active disturbance rejection decoupling control of 4-DOF magnetic bearing

4 仿真试验分析

为了验证所设计解耦控制器的效果，使转子稳定地悬浮在离电磁线圈中心0.125 mm的位置处。在相同的条件下，对比传统的ADRC控制以及基于滑模变结构的SM-ADRC控制效果。控制参数：ADRC中wc=5 000 rad/s，w0=8 000 rad/s；SM-ADRC中，c2=5 000，ξ=2 800，k=2 800。磁悬浮的结构和运行的具体参数值见表1[4]。

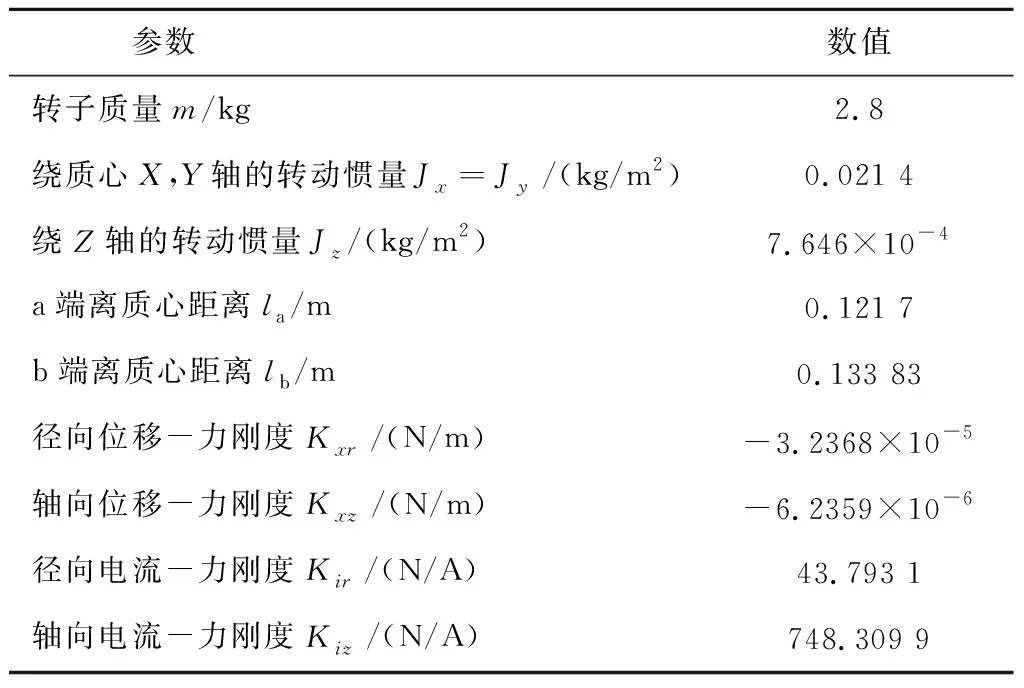
表1 系统变量及参数值

1)位置响应。

图5为在xa方向施加幅值为0.125 mm阶跃信号，ADRC、SM-ADRC两种控制下的悬浮位置阶跃响应曲线，转子在该方向都能悬浮在位置0.125 mm的位置处。由图还可知，SM-ADRC的响应特性要优于ADRC控制，超调量小，系统调节时间短，为0.036 s，ADRC调节时间约为0.05 s。由此可知，对于四自由度的磁悬浮系统，SM-ADRC相比于ADRC在快速响应上得到了提高。

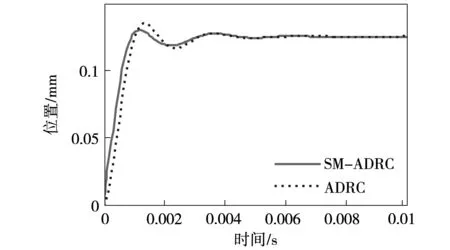
图5 两种控制下的xa位置响应结果对比Fig.5 Comparison of xa position response results under two controls

图6为xa=0.125 mm、xb=ya=yb=0时磁悬浮四自由度解耦前后的控制性能对比，解耦前采用的是分散PID控制，解耦后采用的是SM-ADRC控制，从仿真结果可知，解耦前，由于变量之间存在着耦合特性，虽经过PID控制，xa、xb、ya、yb都出现了振荡的情况，无法控制在所需的目标位置，控制性能很难满足要求；但是经过SM-ADRC解耦控制后xa经过一定的振荡和超调后稳定在了0.125 mm处，xb、ya、yb这3个自由度经过各自的振荡后，都能稳定在给定的目标为0的位置处，说明系统在坐标X、Y方向解耦成功，并达到了较好的效果。

图6 4个自由度的位置响应曲线Fig.6 Position response of the system with 4-DOF

图7为转子两端在该控制下的轴心轨迹图，由图7(a)也可知，在ya方向经过一定波动后回到了目标点(0.125,0)的位置，b端经过一定振荡后归于零点，与图6的分析结果一致。

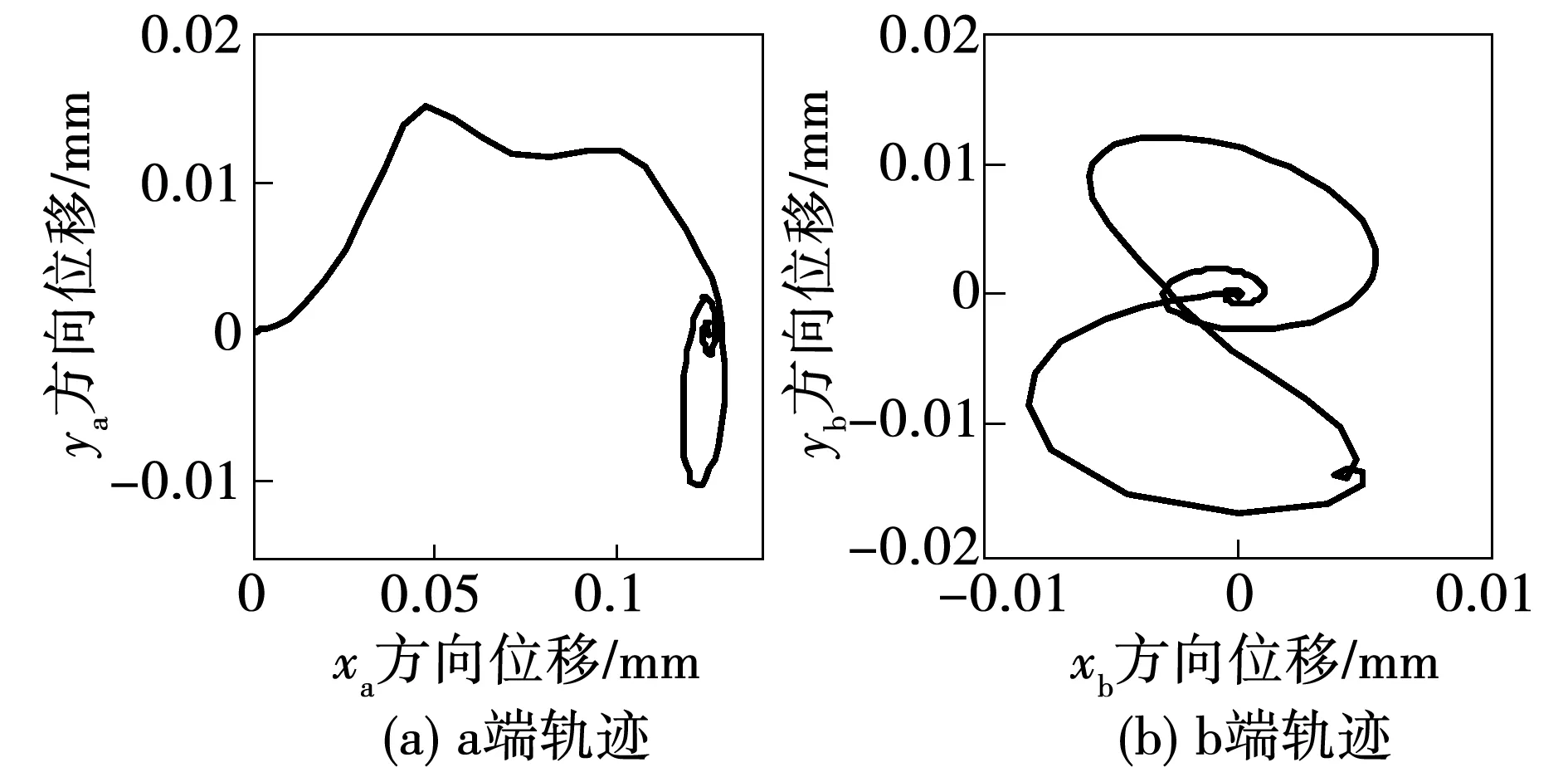
图7 转子a，b两端的运动轨迹Fig.7 Trajectory of the two ends of the rotor “a” and “b”

图8为随着电机转速的升高，转子陀螺效应对系统控制的影响，从图中可知，当电机从0加速到200 000 r/min，在低转速时，陀螺效应项有振荡波动的情况，随着转速的升高，该项趋于0，这说明转速的耦合影响得到了抑制。

图8 陀螺效应随转子转速的影响Fig.8 Influence of gyroscopic effect with rotor speed

图9 xa位置响应下的扩张状态观测器输出Fig.9 Output of the ESO under xa position response

2)抗扰控制。

为了解系统解耦后的抗扰能力，假设各自由度的目标值都设定为0.125 mm，然后在0.01 s时刻在ya的位移方向加入外扰，使其偏离平衡位置0.02 mm的大小，同时观察4个自由度的控制稳定性，由图10可知，ya方向所受的波动最大，经SM-ADRC控制器之后，依然能保持稳定，如图10(c)所示，其余3个自由度都受到扰动，但最终都能稳定在目标位置，如图10(a)、(b)、(d)所示。说明SM-ADRC在负载干扰下能抵御扰动所带来的影响，恢复到之前的平衡位置0.125 mm处，所设计的控制器具有很强的抗干扰能力。

图10 ya方向施加扰动时各自由度的输出Fig.10 Output of each degree when disturbance is applied in the ya direction

图11为在外扰加入的情况下，转子a端的轨迹变化，结果同样显示，加入扰动后转子很快也回到了平衡位置，系统没有静差，具有很好的动态性能。

图11 ya方向施加扰动时转子a端的轨迹Fig.11 Trajectory of end “a” of the rotor when the disturbance is applied in the ya direction

图12 ya方向施加扰动时扩张状态观测器输出Fig.12 Output of the ESO when a disturbance is applied in the ya direction

3)跟踪控制。

为了使系统转子悬浮位置可调，使磁轴承转子跟踪所需要的悬浮高度要求，并验证算法的跟踪性能。在xa方向输入为0.14±0.3 mm，频率为100 rad/s的方波信号，其它自由度设置目标值为0.125 mm。由图13可知，在各自由度上，控制结果都能跟踪到目标值，表明SM-ADRC具有很好的控制跟踪的能力。

图13 xa方向输入方波时各自由度的输出Fig.13 Output of each degree when a square wave is input in the xa direction

图14为在xa方向输入方波的情况下，转子a端的轨迹跟踪，结果同样显示，解耦后的转子很快跟踪到该方向的位移，系统没有静差，同样也具有很好的动态性能。

图14 跟踪控制时转子a端的轨迹Fig.14 Trajectory of end “a” of the rotor during tracking control

图15为跟踪控制时扩张状态观测器的输出，由图15(a)、(b)、(c)可知，在位置控制上，观测值很好地跟踪了输入参考信号的变化，同时在速度和扰动估计上，观测器也能对其进行很好的估计。因此，SM-ADRC可以使系统及时跟踪输入参考量的变化，且输出稳定，同时观测器表现出了较好的观测性能。

图15 跟踪控制时扩张状态观测器输出Fig.15 Output of the ESO during tracking control

通过对3种控制的状态分析得出：SM-ADRC能对磁悬浮系统径向的4个自由度进行解耦控制，并能使转子稳定在所需要的悬浮位置。同时，在位置响应上，其动态特性要优于ADRC控制，系统调节时间短时、超调量小。在抗干扰能力上，SM-ADRC对系统在工作过程中可能存在影响的外扰具有很好的抵抗作用。在位置跟踪上，SM-ADRC同样能对所设定的位置信号进行跟踪。

5 结 论

通过对基于滑模自抗扰解耦控制的理论和仿真分析，可以得出以下结论：

1)本文所提出采用的基于滑模和自抗扰技术的控制能够使磁悬浮轴承转子系统保持稳定，与传统的自抗扰控制相比，系统的位置响应速度快，无超调。

2)基于滑模和自抗扰技术的控制实现了对磁悬浮转子径向4个自由度的完全解耦，并完全消除了高速时陀螺效应的影响。

3)在抗外扰和跟踪性能上，基于滑模的自抗扰控制能有效地对外扰地抵抗外在扰动的干扰，使系统保持稳定；同时系能根据所设定的目标值，对信号进行跟踪。