基于数据驱动的涡轮发动机剩余寿命预测
柳长源, 何先平, 于会越
(哈尔滨理工大学 测控技术与通信工程学院,哈尔滨 150080)
0 引 言
涡轮发动机的工作状态直接影响飞机的性能,而飞机由于其起飞后长时间滞空等客观原因,其发生故障后不管是对人身安全方面的危害,还是经济方面的损失,都是无法估量的。为了保障涡轮发动机的运行的可靠性,并降低飞机的维修成本,美国等航空发达国家早在1977年就将故障预测和健康管理应用于发动机的维修[1]。ISO13881-1定义故障预测为:对设备失效或出现风险的时间点进行估计。而设备的剩余寿命(remaining useful life RUL)[2]指的是设备从初始状态到设备完全失效这一阶段的时间。预先精准的剩余寿命预测能够使航空公司提前做出明智的维护决策,避免永久性损坏,显著的降低了运营和维护成本。
涡轮发动机剩余寿命预测主要有2个方向,1)基于物理模型:在发动机失效原理基础上建立模型后对剩余寿命进行预测操作;2)基于数据驱动,通过采集或者仿真发动机失效过程中的数据,利用算法、机器学习等结合失效阈值进行剩余寿命预测,如基于滑动窗口的算法[3]、基于隐马尔科夫的算法(HMM)[4]、基于K-Means的算法[5]、基于支持向量机的算法(SVM)[6]、基于卷积神经网络(CNN)和长短期记忆网络(LSTM)的算法等[7-8];基于物理模型建立寿命预测模型的泛化性较差,所以本文采用第二种方式进行寿命预测。
基于支持向量回归的算法不能良好利用性能参数对应的提取时间来预测剩余寿命,而且SVR模型的参数较多,在实际应用的在参数设置方面会耗费大量的资源,并且预测效果和算法的效率一般。基于神经网络的算法受其搜索算法的控制,求解空间函数时若搜索步长过小容易陷入局部最优,存在局部极小、收敛速度慢的问题。随着机器学习技术的成熟,集成学习也有了很大的发展。这种通过某些规则将多个机器学习的成果有效的整合在一起的方法也可以应用在发动机寿命预测上。通过使用单边梯度采样和互斥特征绑定对梯度提升迭代决策树(gradient boosting decision tree, GBDT)进行改进,该算法提高了树算法中的残差的近似值,选择拟合损失函数的负梯度的方法来进行寿命预测,在保证预测性能指标的同时大大降低了模型的运行时间,提高了模型的预测效率。
1 梯度提升树模型原理
GBDT模型是利用加法模型和前向分布算法实现学习优化过程的一种集成模型。GBDT预测流程如图1所示。
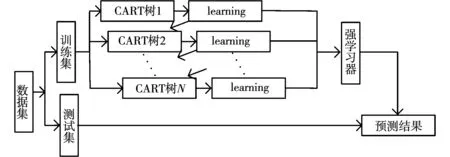
图1 GBDT预测流程Fig.1 GBDT forecasting process
该模型基分类器为分类与回归树(classification and regression tree,CART),集成方为梯度下降(gradient boosting)[9]。GBDT在进行子树构建时将会产生相应的残差,将其数据传输给下一个子树,并且按照子树逐层构建的顺序来进行预测,最终将预测结果相加。
1.1 GBDT概述
GBDT模型在训练过程中不断调整残差,最终通过相加来实现数据的回归。训练数据集表示为
T={(x1,y1),(x2,y2),…,(xN,yN)},xi∈χ⊆Rn。
(1)
式中:x为输入空间;yi∈Y⊆Rn,y为输出空间。损失函数为L(y,f(x)),输出为F(x)。损失函数训练数据集模型可以表示为决策树的加法模型:
(2)
式中:T(x;θm)为决策树;θm为决策树参数;M为树的个数。
模型训练总轮数为M轮,每轮都会有一个弱分类器T(x;θm)产生。弱分类器的损失函数为
(3)
GBDT的每一次迭代都要输入上一次迭代产生的残差,拟合误差会随着迭代次数的增加逐步减小。因此,通过不断的迭代,最终得到一个弱学习器T(x;θm),使样本的损失尽可能变小。
1.2 GBDT的负梯度拟合
Freidman通过采用损失函数的负梯度的方式来模拟最速下降法,从而得到拟合本轮损失的近似值[10],这种方法解决了损失函数拟合方法的问题,最后通过拟合得到一个CART回归树[11]。第M轮的第i个样本的损失函数的负梯度表示为
(4)
利用(xi,rmi)(i=1,2,…,m)估计回归树叶节点区域。将第m颗树的输入空间χi分为j个无交集部分Rm1,Rm2,…,RmJ,每个部分的输出为常量cmj,c为上一轮迭代后决策树的输出值,有
(5)
(6)
(7)
采用线性搜索来估计叶节点区域的值,使损失函数达到极小化,则树由初始状态(6)更新为式(7)。
最终得到回归树为
(8)
1.3 改进的梯度提升树
GBDT具有效率高、精度高等优点,但由于GBDT在处理数据是需要扫描数据集的所有特征,在处理高维度、数据量大的数据集时非常耗时[12]。
本文使用基于梯度的单边采样和互斥特征捆绑这两种算法对GBDT进行改进,改进的GBDT算法能够很好的平衡运行效率和数据量。这种改进大幅度提高了计算速度、降低了内存消耗,也更适应于大数据的回归。
1.3.1 单边梯度采样
单边梯度采样主要是通过减少样本数据,在保证较大梯度样本数据不变的同时,随机采样部分的小梯度样本,不仅极大地提升了计算速度,也有效地保证了计算精度。
较大梯度的数据能够为计算信息增益的提供较大的帮助,当某个样本点的梯度已经减小到足够小时,此时该样本的训练误差已经达到要求,即该样本已经被充分训练。因此,使用常量乘法器放大未充分训练。
为了保证数据的总体分布,首先针将数据的绝对值进行依次减少的顺式排序,然后选取前a个样本作为较大梯度的数据子集A,并对其余样本进行随机采样,在剩下的较小梯度数据中选取b个样本实例作为数据集B[13]。最后,通过计算所选取的a+b个样本数据,获得信息增益,其计算方式为
(9)
1.3.2 互斥特征绑定
互斥特征绑定的定义是为提升计算效率,而将不完全互斥的特征进行融合捆绑来降低特征数量。为减少计算量,将特征按照非零值进行排序,非零值越多,越容易发生互斥,并将不完全发生互斥的2个特征进行捆绑,并使用特征合并法来降低算法复杂度。通过互斥绑定后的复杂度为O(数据×绑定后特征数目),此时使用的绑定后特征数目已经大幅度降低,使得模型在保证精度的情况下减少训练时间。改进的GBDT算法存储的不是连续的特征值而是离散的直方柱。通过向指定的直方柱添加偏移量解决原始特征值可识别问题。设定特征数组总共包含2个特征C,D。若C∈[0,8],D∈[0,16],向特征向量D添加8个单位的偏移量,则绑定后的范围为[8,24]。
2 基于梯度提升树的寿命预测
2.1 实验数据介绍
本实验采用的是大型涡轮风扇发动机GE90的仿真数据。该数据集共有4个子集,各个子集的操作模态和故障数目各不相同,每个子集都由200个及以上完整的运行单元组成。每个完整的运行单元由26维特征数据构成。每一维数据都可以描述给定时间点上引擎状态或受到其他列传感器影响的数据。该矩阵第一列表示发动机ID,第二列表示发动机运行次数,接下来的三列为运行环境设置,余下的21列则对应传感器数据。4个仿真数据子集的详细设置如表1所示。
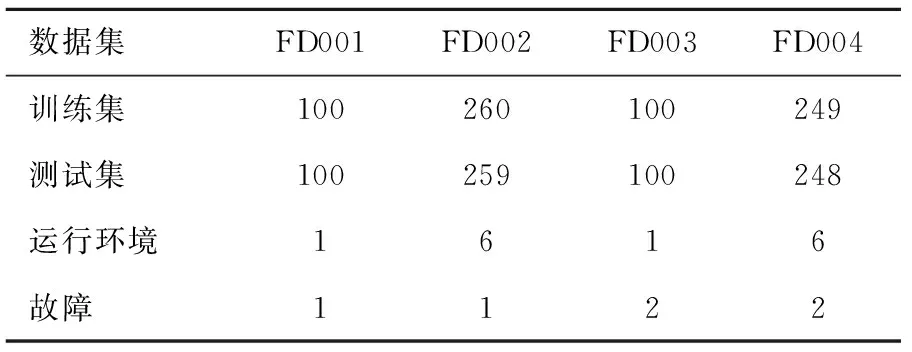
表1 C-MAPSS数据集
为了衡量算法效果,本文使用两种评价指标来进行衡量。惩罚函数(Score)的大小衡量了寿命预测的合理性,有
(10)
而均方根误差(RMSE)反映了预测寿命与实际寿命的拟合程度,表示为
(11)
其中Ei为真实寿命与预测寿命之差,当Ei越小,即Score与RMSE越小,预测寿命越准确,预测效果越好。
2.2 剩余寿命估计目标函数
早期的余寿预测领域所使用的目标函数大多数为一次递减函数,这种函数只能表示设备损耗与设备性能之间的线性下降的关系,无法显示设备的损耗与时间的关系。机械设备工作初期设备磨损较小,机械设备在一段时间内工作在稳定状态。而机械设备在经过长时间的磨损之后,设备性能逐渐降低,当磨损达到一个临界值,设备的使用寿命逐渐下降[14]。因此,使用分段目标函数能够更加准确的表示剩余寿命的发展趋势,如图2所示。
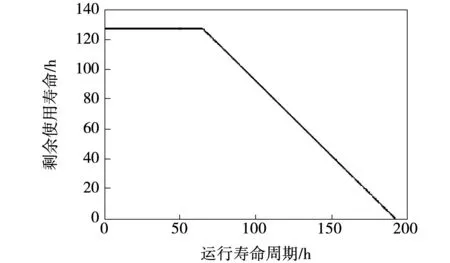
图2 剩余寿命估计目标函数Fig.2 Remaining useful life of objective function
本文采用的分段函数是通过实验确定,对于GE90的仿真数据集,其最长使用寿命为130能够得到最优的预测性能。对于一个完整运行寿命周期为200的实验,设其最初运行时为最大使用寿命130,运行一段时间后到达第70个检测采样周期,此后电机寿命开始逐渐下降,呈线性衰减,直到实验结束时剩余使用寿命衰减为0。
2.3 数据归一化
数据处理根据数据自身具有的特性,避免特征绝对值上小数据被大数据平均掉,帮助模型更好的适应数据。
崇明岛内河水位主要是由沿江水闸控制的。在枯水期(1月、2月、11月、12月),岛上的水闸一般采取西水东调、南引北排的方式进行调水工作;在平常的3月、4月、5月、10月,则根据长江内的水质情况,采取选择性的引排方式,即选择符合引水标准的南沿水闸进行引水、北沿水闸适当排水。而在主汛期主要是以南引北排的方式进行,以控制内河水位。
归一化方程式为
(12)
式中:μi表示平均值;σi表示标准偏差。对发动机的21维传感器参数进行归一化处理后如图3所示。
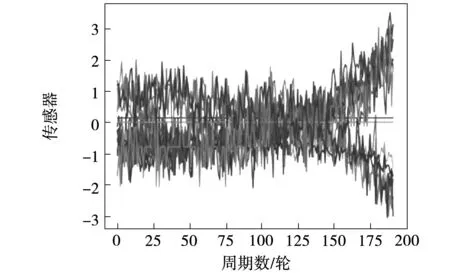
图3 归一化处理Fig.3 Normalization
3 实验结果分析
本实验的实验环境如表2所示。
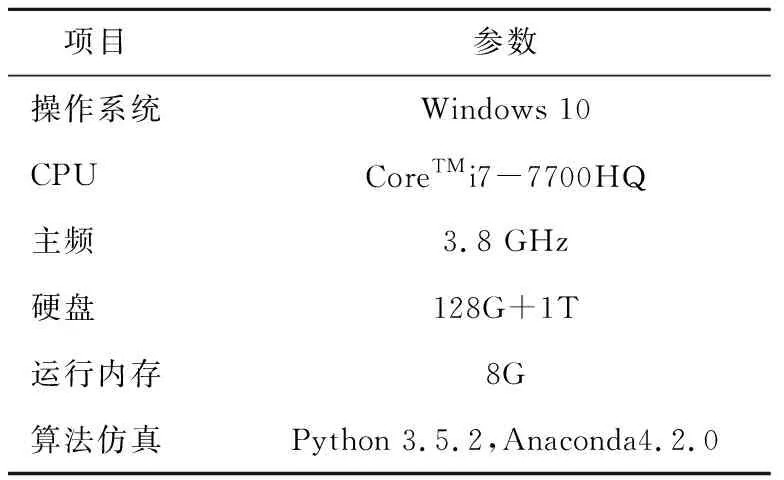
表2 实验环境
3.1 工况一性能分析
图4为改进的GBDT模型在FD001数据集和FD003数据集中的Score变化情况,这两种数据集均工作在模态1下。实验结果表明,改进的GBDT算法在FD001数据集和FD003数据集的Score指标上表现极其优越。FD003数据集在Score指标表现上较FD001数据集表现稍差,这是由于FD003数据集是在高压压气机和风扇均故障下收集得到的。

图4 FD001和FD003的Score对比Fig.4 Comparison of Score between FD001 and FD003
图5为不同算法在FD001数据集和FD003数据集下的评价指标直方图。由图可以看出,改进后的GBDT算法在2种数据集中的RMSE值偏高,但由于RMSE值与Score值的相关性,综合总体情况,改进后的GBDT算法更加适用于提前发出寿命预警,而对于飞机发动机而言,更早的发现发动机设备的受损情况能够更早的进行设备维护工作,因此较早提出寿命预警是合理的。
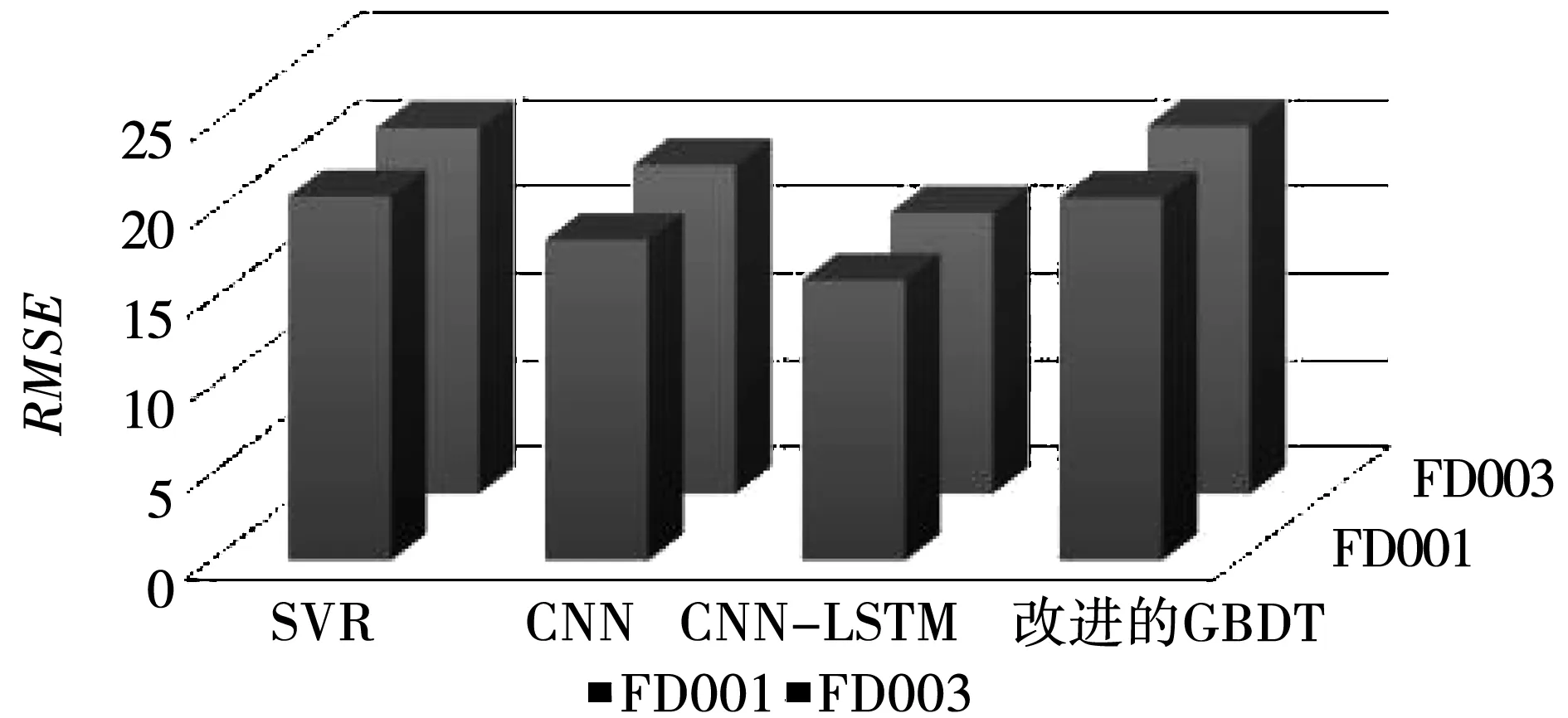
图5 FD001和FD003的RMSE对比Fig.5 Comparison of RMSE between FD001 and FD003
3.2 工况二性能分析
FD002数据集和FD004数据集在模态6下工作。通过对比实验可知,改进GBDT模型的Score指标较剩余寿命预测领域经典算法提升幅度小,各个算法的Score指标对比如图6所示。
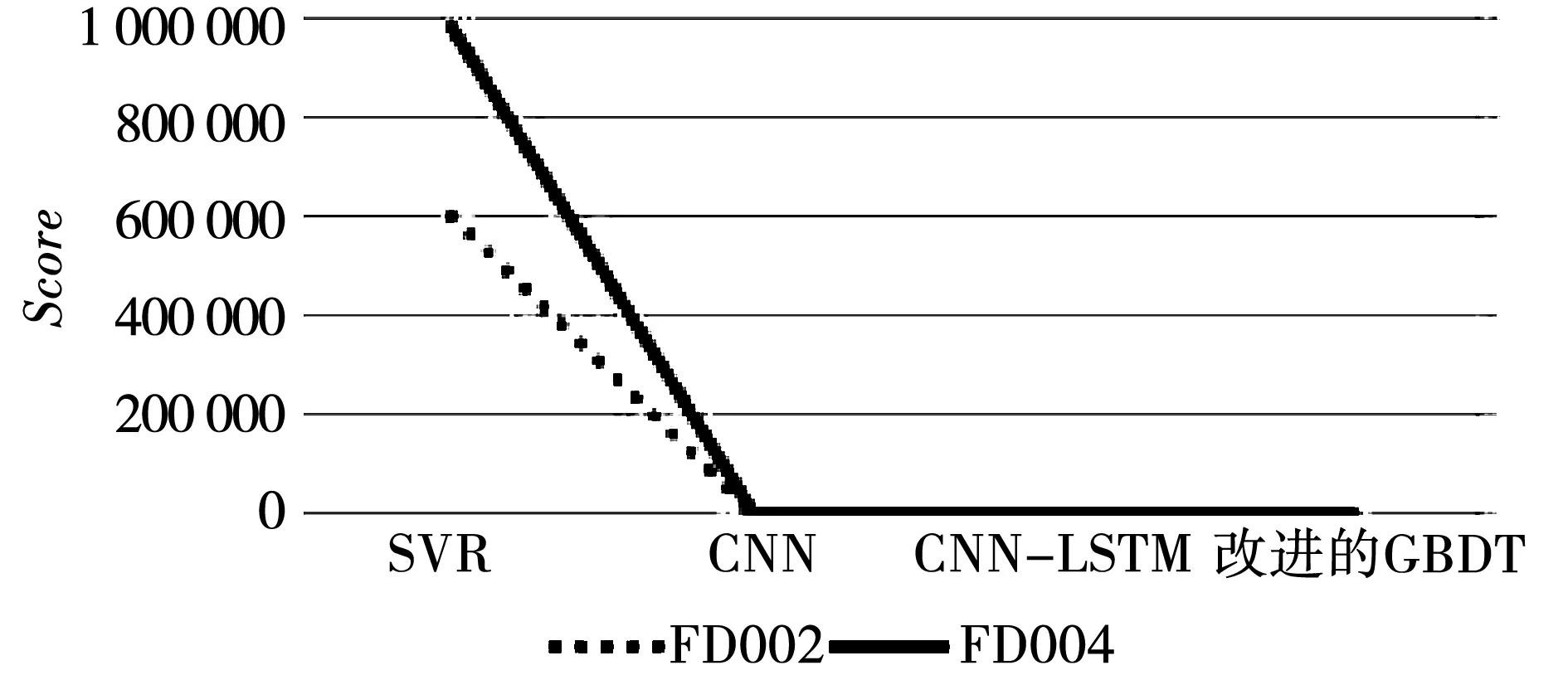
图6 FD002和FD004的Score指标对比Fig.6 Comparison of Score between FD002 and FD004
复杂工况下改进的GBDT的RMSE表现较差,FD002数据集较FD004数据集稍好一些。RMSE直观对比如图7所示。更复杂的情况导致拟合较为困难,2个数据集下改进GBDT的RMSE指标都是仅仅比SVR表现略好。将两种指标进行总体分析,改进的GBDT模型在复杂工况下,Score值较其他算法略有提升,RMSE较经典算法略有提高,能够在发电机剩余寿命结束前发出预警。

图7 FD002和FD004的RMSE对比Fig.7 Comparison of RMSE between FD002 and FD004
通过分析改进的GBDT与其他算法在不同工况下的性能,可以得出改进的GBDT算法在Score指标上有较为明显的提升,能够较好的预测发动机的剩余寿命情况,尤其是在故障较少的FD001和FD002数据集下表现较为优异,算法预测更为准确,而在复杂工况的下提升幅度较小。改进的GBDT算法在RMSE指标上也是在简单工况的表现更好。因此,改进的GBDT算法能够提早完成预测,适用于发动机剩余寿命预测。
从C-MAPSS中的FD001、FD002、FD003、FD004中分别随机选择一个时间周期,在保证其测试结果完整的情况下进行结果可视化,真实剩余寿命与预测剩余寿命的对比图如图8所示。其中折线为根据分段函数设定的发动机真实寿命,另一条为改进的GBDT预测寿命。
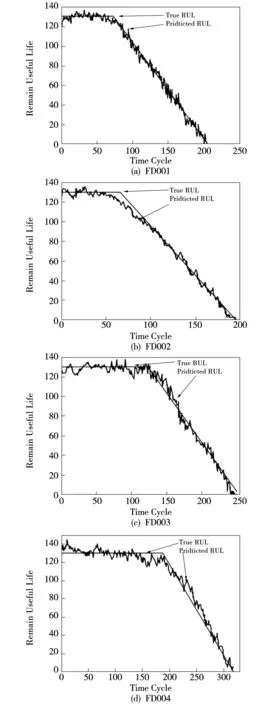
图8 剩余使用寿命预测Fig.8 Prediction of remaining useful life
3.3 运行速度与评价指标分析
CMAPSS数据集的维数为26维,对一段完整的生命周期进行一次剩余寿命预测需要将近两百个循环,大量的数据在一定程度上保证了预测效果但也使得运行效率并不理想。通过将互斥程度较小的特征进行捆绑,减少特征维度,达到计算效率的提升。表3为改进后的GBDT模型与其他算法在不同工况下的剩余寿命预测时间。
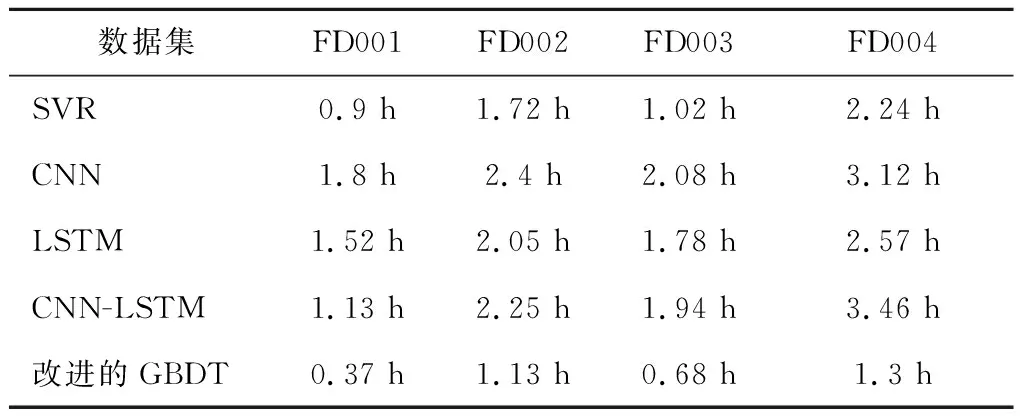
表3 不同模型运行时间
为了进一步验证模型的性能,做了多种不同的算法性能对比,Score指标结果对比如表4,RMSE指标结果如表5。
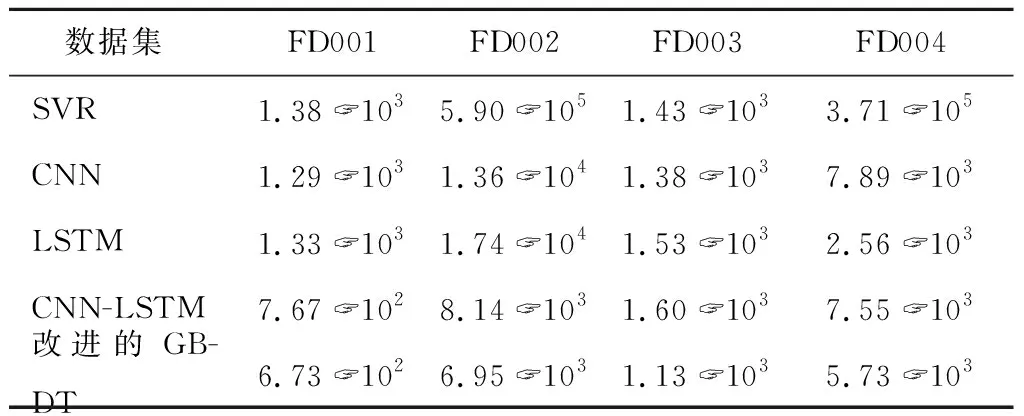
表4 Score指标结果

表5 RMSE指标结果
通过以上指标对比分析,改进的GBDT模型在不同数据集上的运行时间有较大幅度的提升,Score指标较几种现有算法均有明显提升,RMSE指标在FD002和FD004数据集上略有提升,在FD001和FD003数据集上略有下降,RMSE指标除SVR较差外,其他几种方法与改进的GBDT算法大体相仿。
4 结 论
本文通过比较改进的GBDT模型与现有的SVR、CNN、LSTM、CNN-LSTM算法在不同工况下的性能指标,得到改进的GBDT模型在Score指标上有大幅度提升,RMSE指标相仿。结合实际情况可以得出改进的GBDT算法倾向于更早提出寿命预警,更适用于飞机发动机剩余寿命预测领域。同时,在保证预测性能指标的情况下,改进的GBDT模型在4个子数据集下的运行时间较经典算法都下降60%以上,表明本文所提出的算法具有较高的实用价值。

