基于改进PSO与广义五阶CKF算法的PMSM无传感器控制

张荣芸， 郑常胜， 时培成， 赵林峰， 龚长富， 周成龙

(1.安徽工程大学 机械与汽车工程学院，安徽 芜湖 241000；2.安徽工程大学 汽车新技术安徽省工程技术中心，安徽 芜湖 241000； 3.合肥工业大学 汽车与交通工程学院，合肥 230009；4.安徽工程大学 高端装备先进感知与智能控制教育部重点实验室，安徽 芜湖 241000)

0 引 言

永磁同步电机(permanent magnet synchronous motor，PMSM)因具有优良的控制性能而广泛应用于汽车的自动化控制中。然而，其精确控制所需转子转速和位置信号一般由传感器获得。传感器的使用使电机具有结构复杂、可靠性低、成本高和维护难等不足，限制了其应用范围，降低了其系统鲁棒性。因此，无传感器控制技术成为了现代电机控制技术的一个重要研究方向。

随着高性能数字信号处理技术的飞速发展，许多学者对PMSM转速估计进行了广泛研究。在零速或低速条件下，常用高频注入法[1]对电机转速进行估计，但该方法需基于电机的凸极效应，且在中高速运转时存在高频噪声，估计精度较低。而在中高速条件下，常用基于模型的观测器法来对电机转速进行估计[2-3]。观测器方法通过建立反电动势或磁链观测器，获得转子位置与转速信息，但在模型搭建的过程中需要对电流信号进行微分，这会使噪声信号放大，因此需要加入滤波环节，增加了算法的设计和调试工作。虽然，滑模观测器法有良好的动态性能，但开关函数的存在带来了系统抖振问题，影响了估计的精度。另外，还有扩展卡尔曼滤波(extended Kalman filter, EKF)算法[4-5]、无迹卡尔曼滤波(unscented Kalman filter,UKF)算法[6-7]和容积卡尔曼滤波(Cubature Kalman fitler,CKF)算法[8-9]。EKF算法具有较好的估计效果，但该方法通过对非线性系统进泰勒级数展开取第一项来对非线性系统线性化，存在高阶截断误差，同时还需计算复杂的Jacobian矩阵，计算量大实现起来困难。UKF算法虽然不需要计算复杂的Jacobian矩阵，但由于在数值计算过程中存在舍入误差，会引起协方差不对称或非正定等不足，容易出现发散。CKF算法通过权值与容积点的计算，经过非线性方程的转换后，产生新的容积点来给出下一时刻的状态估计，不需要对系统进行线性化处理。可用于精确的电机转速估计，但CKF算法是基于三阶球面-相径容积规则来近似高斯权值积分的，其估计精度只能达到三阶。

另外，PMSM控制精度的提高，还可以通过改善其控制方法来实现。常见的PMSM控制方法是采用传统的PI控制，其控制结构简单，是当今工业控制中应用非常广泛的控制算法。虽然PI控制有一系列优点，但传统PI控制达到满意控制效果所需的控制参数难以准确获得。目前对PI参数进行优化的主要方法有：试凑法、专家规则法[10]、模糊控制[11]以及遗传算法[12]等。其中，传统的试凑法需要反复对PI参数进行调试，费时费力且误差较大；专家规则法则与经验知识相关，需要不断整理和更新专家知识库；模糊控制对于模糊规则和隶属度函数的要求较高；遗传算法较为复杂且易早熟收敛。因此，虽有较多方法用于PI参数的优化，但都存在一定的不足。

综上所述，针对电机转速估计精度及PI参数优化的问题，本文提出一种基于改进粒子群优化PI参数与广义五阶CKF的PMSM无传感器控制方法。在推导出PMSM矢量控制中的电流环与速度环传递函数的基础上，并以此为适应度函数，采用基于柯西变异的改进粒子群算法对速度环传递函数中的PI参数进行优化；推导广义五阶CKF算法，对PMSM转速进行估计，实现基于改进粒子群优化PI参数和广义五阶CKF的PMSM无传感器控制；最后，对本文提出的无传感器控制算法进行电机台架实验，相比于CKF，广义五阶CKF对PMSM的转速估计精度更高，且改进粒子群优化PI参数后的PMSM无传感器控制效果较优化前也有明显提高。

1 PMSM数学模型

根据表贴式永磁同步电机的电压、磁链、电磁转矩和机械运动方程，可得PMSM非线性数学模型在静止坐标系下的状态空间表示为：

(1)

式(1)中的系数矩阵为：

其中：θ、ω为电机转子位置和转速；ψf、Rs、L分别是转子永磁体磁链、定子电阻和电感。

根据Euler法，将PMSM的数学模型离散化可得：

(2)

设采样时间为T，则式(2)中：

(3)

(4)

(5)

根据式(2)～式(5)，就可建立起PMSM的离散数学模型。

2 PMSM无传感器控制

本文采用基于改进粒子群优化PI参数和广义五阶CKF算法来构建PMSM无传感器控制。该控制策略采用id=0的矢量控制，为了改善控制效果，利用基于柯西变异的改进粒子群算法对转速环中的PI参数进行优化；对于控制中所需要的转子转速和位置信号，利用所建立的PMSM数学模型，运用广义五阶CKF对其进行估计得到。本文对PMSM采用的无传感器控制如图1所示。

图1 基于改进粒子群优化PI参数与广义五阶CKF的PMSM无传感器控制系统Fig.1 PMSM sensorless control system based on the improved particle swarm optimization PI parameters and generalized fifth-order CKF

2.1 改进粒子群优化算法

粒子群算法(particle swarm optimization，PSO)属于群智能算法，是一种进化计算技术，源于对鸟群捕食行为的研究。相比于其他智能优化算法，PSO具有迭代速度快、鲁棒性好等优点。因此，本文采用PSO来对转速环PI控制参数进行优化。

1)PSO算法。

首先在可行域中初始化一群粒子，每个粒子都代表极值优化问题的一个潜在最优解，用位置、速度和适应度三项指标表示该粒子的特征。粒子在解空间中的运动，可利用个体极值(Pbest)和群体极值(Gbest)更新个体的位置来进行描述。个体极值是指个体在所经历位置中得到的适应度值最优位置，群体极值是指种群中的所有粒子搜索到的适应度最优位置。粒子每更新一次位置，就计算一次适应度值，如果其值比该粒子之前的适应度值都小，则更新适应度值、个体极值，且每次更新后，将所有粒子中对应的最小适应度值来更新群体极值。且在每次迭代过程中，粒子自身速度和位置是通过个体极值和群体极值来进行更新的[13]。

初始化时假设在D维搜索空间中有m个粒子,其第i个粒子的位置矢量为[14-15]

(6)

其速度矢量为

(7)

第i个粒子搜索到的最优位置为

(8)

整个粒子群搜索到的最优位置为

(9)

第i个粒子的位置和速度更新为：

(10)

其中：w为惯性因子，为非负数；c1，c2为加速常数，为非负数。r1，r2为介于[0，1]之间的概率值。

2)基于柯西变异的改进PSO算法。

为了增加传统PSO算法种群的多样性和避免陷入局部最优，本文将柯西变异算子引入到传统PSO算法中，也即是当式(10)中的r1、r2为均小于或等于0.1时，就进行柯西变异，增加PSO种群以获得全局最优[16]。

一维柯西分布的概率密度函数为

(11)

其中λ为大于0的系数，一维柯西分布的分布函数为

(12)

当λ=1时，式(12)为标准柯西分布。

引入柯西变异因子φ后，第i个粒子的位置和速度更新可表示为：

(13)

式中C(0,1)为标准柯西分布函数产生的随机数。

为了提高柯西变异PSO的收敛速度和使其快速跳出局部最优，本文采用变化的柯西变异因子φ，当在PSO算法的早中期，采用较大的φ来跳出局部最优；当在PSO算法的后期，采用较小的φ来提高收敛速度。

因此，柯西变异因子φ可以表示为

φ=(G-n)/G。

(14)

式中：G为最大迭代次数；n为当前迭代次数。

之后，判断更新后的粒子是否满足迭代终止条件，若满足则输出最优解；若未达到终止条件，则从新计算适应度，并进行位置与速度更新。

柯西变异PSO算法的流程如图2所示。

图2 改进粒子群算法示意图Fig.2 Diagram of the improved particle swarm optimization algorithm

为了对比分析PSO算法和基于柯西变异的改进PSO算法的收敛速度，以2.2节中PMSM转速环传递函数为适应度函数，得到迭代次数与适应度函数值的关系曲线如图3所示。

由图3可以看出，相比于普通PSO算法，基于柯西变异的改进PSO算法在寻找目标函数的最优解时，能够在更少的迭代次数下寻找到最优解。其中，普通PSO算法在330代左右得到最优解，而改进PSO算法在100左右就找到了最优解。另外，由图中曲线走向可以看出，普通PSO算法在寻优时，会短时陷入局部最优(例如第20代到第32代)，而改进PSO算法则可以有效避免这种情况出现。因此，基于柯西变异的改进PSO算法相比于普通PSO算法具有更快的迭代速度和更好的全局搜索能力。

图3 PSO算法与改进PSO算法的迭代速度对比曲线Fig.3 Iterative speed comparison curves of the PSO algorithm and improved PSO algorithm

2.2 PMSM转速环传递函数

对PMSM进行控制，常采用PMSM磁场定向双闭环控制策略，它是一种含有电流环和转速环的双闭环系统。本文以该双闭环系统的转速环传递函数来作为PSO算法的适应度函数。

根据文献[17]，工程设计PMSM双闭环控制的原则是先内环后外环，设计步骤是：先从电流环开始，对其进行必要的变换和近似处理后，对电流环进行校正(一般校正成2阶系统)，最后按动态性能指标要求来确定电流调节器的参数。电流环设计完成之后，把电流环等效成转速环中的一个环节，再用同样的方法设计转速环，一般将其校正为3阶系统。因电流环的控制对象为PWM逆变器和电机电枢回路，且电机的传递函数一般不随外部负载变化，具有稳定的结构，故令PI调节器中的Kic=Kpcτc，可得到电流环的开环传递函数为

(15)

其中：Kpc为电流环PI调节器比例系数；KPWM为逆变器的放大倍数；TPWM为PWM逆变器的开关周期；Lq和Rs分别为电机电感和电阻。

再令τc=Lq/Rs，可以将式(15)转化为二阶系统的电流环闭环传递函数

(16)

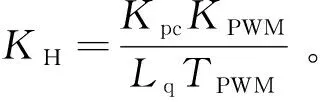
在设计转速环时，可以将电流环的传递函数看作是简单的一阶环节。根据上式电流环闭环传递函数和转速环具有较低截止频率的特点，可以将电流环闭环传递函数去掉高次项进行降阶近似为

(17)

(18)

经过以上步骤即可得到PMSM的转速环传递函数，以此为适应度函数，接着利用改进粒子群算法对转速环PI参数进行优化，即可得基于改进粒子群PI参数优化的PMSM控制系统。

2.3 广义五阶CKF算法

目前，CKF对高斯滤波中的高斯积分采用三阶球面-相径容积规则来进行近似求解，可以达到三阶估计精度。本文为提高PMSM转速的估计精度，运用广义五阶容积规则来对高斯积分进行求解。对于离散系统，将贝叶斯估计基本理论与广义五阶容积规则相结合，即可推导出广义五阶CKF滤波方法。

广义五阶容积积分公式如下[18-20]

n≥2。

(19)

(20)

由此可得式(20)的唯一解为：

将式(19)转化成标准高斯分布的形式，可得

(21)

可得到容积点集和相关权重如下：

1)时间更新。

①计算容积点xk,i(i=0,1,…,2n2+1)：

(22)

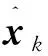
②计算通过状态方程传递后的容积点xk+1/k,i：

xk+1/k,i=f(xk,i)。

(23)

③计算k+1时刻的状态预测值：

(24)

④估计k+1时刻的状态误差协方差矩阵Pk+1/k：

(25)

2)量测更新。

①计算更新后的状态容积点xk+1/k,i：

(26)

其中，Sk+1/k为Pk+1/k经过Cholesky得到的矩阵，i=1,2，…,2n2+1。

②计算通过测量方程传递的容积点yk+1,i：

yk+1,i=h(xk+1/k,i)。

(27)

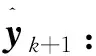
(28)

(29)

⑤计算k+1时刻的滤波增益矩阵Kk+1：

(30)

(31)

⑦估计k+1时刻的状态误差协方差阵Pk+1：

(32)

给定初始值，就可以经过上述流程进行广义五阶CKF估计，其流程图如图4所示。

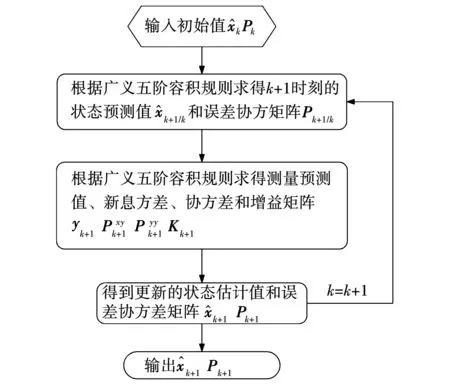
图4 广义五阶CKF的流程图Fig.4 Flow chart of the generalized fifth-order CKF

3 实验验证

为验证所提PMSM无传感器控制方法的实际控制效果，搭建了如图5所示的电机实验台架，实验台主要由上位机、电机驱动实验箱和永磁同步电机组成。在上位机MATLAB/Simulink环境中打开并生成基于CKF和广义五阶CKF算法的PMSM无传感器控制模型代码，通过CCS6.2编译后生成可以在DSP中运行的C代码，再通过连接上位机与实验台的仿真器将代码下载到电机实验箱中的TMS320F28335DSP之中，电机控制箱通过控制逆变器输出驱动信号，控制PMSM工作。上位机可以通过串口工具来接收实验数据，进行参数在线调节，控制PMSM的转速。

图5 电机实验台架Fig.5 Motor test platform

实验时工况为电机转速由800 r/min阶跃到1 000 r/min的转速突变工况，实验结果如图6～图11所示。

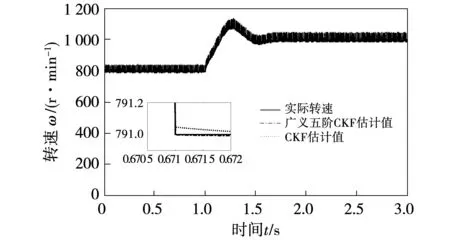
图6 转速估计曲线Fig.6 Speed estimation curve of experiment

图6和图7为实验时分别采用CKF与广义五阶CKF算法进行PMSM转速估计及其估计误差的对比曲线。由图可知，在转速阶跃时，广义五阶CKF算法可以稳定的估计出电机的转速。当电机的转速由800 r/min阶跃至1 000 r/min时，转速估计误差会增大一些，但很快稳定下来，并且整个过程中广义五阶CKF算法的估计误差都较小。因此，实验验证了广义五阶CKF算法在转速突变时，相较于CKF算法，其估算精度更高，对转速突变具有较好的适应性。

图7 实验转速估计误差曲线Fig.7 Speed estimation error curve of experiment

图8和图9为实验时分别采用CKF与广义五阶CKF算法进行PMSM位置估计及其估计误差的对比曲线。由图可知，实验中广义五阶CKF算法可以准确的估计出电机的转子位置，并且在转速突变过程中，其估计精度都要比CKF算法高。表1为转子转速和位置误差的方差对比，反映了转速和位置误差与零的偏离程度，从表中可以看出广义五阶CKF的方差都要比CKF的小，说明其估计的精度比CKF要高。因此，实验结果进一步验证了本文所提的利用广义五阶CKF算法来对PMSM的转子位置进估计的方法，有更高的估计精度。

图8 实验转子位置估计曲线Fig.8 Rotor position estimation curve of experiment

图9 实验转子位置估计误差Fig.9 Rotor position estimation error curve of experiment

表1 转子转速与位置误差的方差对比

图10和图11分别表示实验时转速环PI参数分别采用基于柯西变异的改进粒子群、普通粒子群和无粒子群优化且均采用广义五阶CKF算法来对PMSM转速和转子位置进行估计的误差对比曲线。由上图可以看出，相较于普通粒子群算法，基于柯西变异的改进粒子群算法优化的广义五阶CKF算法在实验中转速和位置估计的误差都要比普通粒子群算和无粒子群算法的要小。并且在转速突变时，本文提出的基于改进粒子群优化的广义五阶CKF算法依然能够进行精确的估计，具有较小的误差。表2表示在实验时，转速环PI参数采用3种算法优化的广义五阶CKF算法的转速和转子位置误差的方差，从表中数值能够说明基于柯西变异的粒子群优化的广义五阶CKF算法的方差要小于另外两种方法，说明其能够提高PMSM转速的控制精度。因此，实验结果说明对PMSM转速环PI参数利用基于柯西变异的改进粒子群算法进行优化，是能够明显提高PMSM转速控制精度的。

图10 实验3种优化方法下转速估计误差对比曲线Fig.10 Comparison curves of the speed estimationerror of experiment under three optimization methods

图11 实验3种优化方法下转子位置误差对比曲线Fig.11 Comparison curves of the rotor position estimation error of experiment under three optimization methods

表2 3种优化方法下转子转速与位置误差的方差对比

4 结 论

为了提高PMSM无传感器控制效果，本文主要利用所推导的转速环传递函数为适应度函数，利用基于柯西变异的改进粒子群算法对PMSM转速环的PI控制参数进行了优化；并利用广义五阶容积规则推导出了广义五阶CKF算法，最后构建了基于改进粒子群算法优化PI参数和广义五阶CKF的PMSM无传感器控制方法，并进行了电机的台架实验。结果表明，广义五阶CKF算法比传统的CKF算法在对PMSM进行转速和位置估计时，具有更加良好的估计精度，并且通过对转速环PI参数优化前后的基于广义五阶CKF算法对PMSM转速和位置进行误差对比实验分析中，可知通过对转速环PI参数的优化能够有效提高PMSM的控制效果。

该算法不仅可以应用在车用永磁同步电机的控制中，对于工业领域内其他行业的电机控制也可以应用。接下来将对该算法实时性的进一步提高进行研究。