永磁电磁混合Halbach阵列空间磁场三维解析计算及参数分析

罗成， 朱开锋， 张昆仑， 靖永志

(1.西南交通大学 电气工程学院，成都 611756；2.西南交通大学 磁浮技术与磁浮列车教育部重点实验室，成都 611756；3.成都衡力磁电科技有限公司, 成都 610207)

0 引 言

自Halbach阵列被美国劳伦斯伯克利国家实验室Klaus Halbach教授提出以来[1-2]，已成功应用于粒子加速器、自由电子激光装置、电机等领域[3-5]。1998年美国科学家R.F.Post等设计出基于永磁Halbach阵列的Inductrack电动悬浮系统，利用Halbach阵列磁场一侧增强，一侧削弱的特性，可以为列车提供足够悬浮力的同时大大减少对车载乘客的磁场辐射[6]。但由于其自身的临界阻尼特性和空间磁场不可控，在受到外界干扰时，容易产生振荡[6]。为了达到对永磁电动悬浮系统空间磁场的调节控制，以实现永磁电动悬浮系统动态稳定悬浮， Ham提出了一种永磁体与电磁铁间隔排列的新型Halbach阵列，通过电磁铁线圈电流控制磁场大小，但其控制线圈安匝数过大而难以应用于实际工程中[7]。Han采用电磁铁Halbach阵列与永磁体Halbach阵列并行安装于车上，但存在永磁体Halbach阵列和电磁铁Halbach阵列磁场耦合问题，且未给出含端部效应的空间磁场解析式[8]。

基于以上研究，本文作者研究一种结构简单且工程更为实用的永磁电磁混合Halbach阵列。其通过在永磁体表面缠绕有源常导线圈，实现对Halbach阵列空间磁场的调节控制。

主要考虑的是变极电机与不变极电机的差价。根据上海电机厂提供的参考价格,TL 1600—28/56同步电动机的价格约为150万元/台，而TL1600—28同步电动机的价格约为100万元/台,则每台变极电机要多投资 50万元，10台电机共计500万元；因电机体积增大而导致土建增加的经费约 60万元，10台合计600万元；其余费用与同转速发电相同。

对于Halbach阵列空间磁场的计算，R.F.Post、李春生等[6,9]将永磁Halbach阵列视为理想结构，其空间磁场近似为正弦磁场，不考虑各次谐波的影响。在小气隙或短阵列时，由于空间谐波和端部效应的影响将产生较大误差。Han等利用傅里叶分解求得无限长永磁Halbach阵列空间磁场，分析不同气隙下四模块与八模块Halbach阵列空间磁场谐波，但不能反映有限长阵列的端部效应[8,10]。宋玉晶等将含端部效应的有限长永磁Halbach阵列视为一个周期，构建伪周期函数，对磁化强度进行傅里叶分解，结合麦克斯韦方程求得含端部效应的有限长永磁阵列空间磁场，但计算过程较复杂[11-12]。陈殷利用磁荷法对有限长永磁Halbach阵列空间磁场进行计算，但磁荷法存在较多的积分运算，导致计算速率较慢[13]。文献[13-14]利用基于磁介质分子环流假设的面电流法对有限长永磁Halbach阵列空间磁场进行计算，其主要通过磁场叠加运算求得含端部效应的空间磁场。文献[15-20]通过对磁化强度进行傅立叶分解，结合麦克斯韦方程，建立标量磁位方程，求得圆弧形单层Halbach阵列及双层Halbach 阵列永磁电机空间磁场的解析表达式。

在以上研究的基础上，本文首先利用毕奥-沙伐定律求得线圈电流在空间产生的磁场，接着利用基于磁介质分子环流假设为基础的面电流法对永磁体在空间产生的磁场进行求解，二者叠加求得永磁电磁混合Halbach阵列空间磁场的三维(three-dimensional，3D)解析表达式；建立相应的3D有限元模型，对解析表达式的正确性进行了验证；最后对线圈所占宽度、线圈电流密度对空间磁场的影响进行了分析。

药物是拯救人们于疾病困境中的物质,随着医疗水平的提升,现阶段临床所用药物均具有较高的安全性和较显著的疗效,保障了人们的生命健康。临床药理学是一门研究药物与人体的相互作用及其在人体内环境中作用机制的学科,主要内容为药理学和临床药学,研究方向包括药动学、药效学、毒副反应、作用机制及药物相互作用规律等,在这个学科的研究中,最基础也是最重要的一个技术,就是色谱技术[1]。在现代化科学技术体系中,色谱技术是一种潜力巨大、适用范围广的生物样品测定分析方法,被广泛应用于在环境学科、生化药物、化工生产等领域的物质分析工作中,为这些行业的发展提供了技术支持。

1 永磁电磁混合Halbach阵列

图1为所研究的永磁电磁混合构成的Halbach阵列示意图及参考坐标系Oxyz。图中，τ为极距，l、w、h分别为永磁体的长、宽、高，σ为线圈所占宽度，为方便加工制造，Halbach阵列模块xy截面为正方形，即h=w+2σ。

图1 永磁电磁混合Halbach阵列示意图Fig.1 Schematic view of the permanent magnets and electromagnets hybrid Halbach array

2 空间磁场计算

为便于计算，设永磁体充磁均匀，磁化强度为常数。且忽略线圈填充率，线圈电流等效成体电流。

由图3(b)，可得x、y分量磁场大小为：

当磁化方向为x反方向时，线圈电流由体电流V、VI、VII、VIII表示，设体电流V的体密度为Jx，则体电流VII的体密度为-Jx，如图4所示。

2.1 Y方向磁化

当磁化方向为y方向时，设永磁体磁化强度为M，线圈电流由体电流I、II、III、IV表示，如图2所示。线圈电流在空间中产生的磁场可等效为体电流I、II、III、IV在空间产生的叠加磁场。

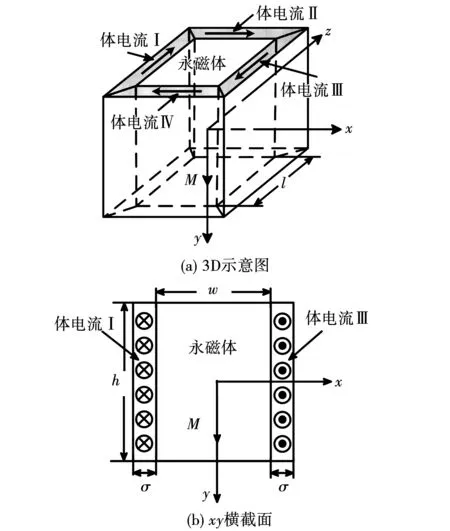
图2 Y方向磁化单体模块Fig.2 Y direction magnetization monomer module

如图3(a)，利用毕奥-沙伐定律可求得体电流I中电流元Jydadb在空间任意点P(x,y,z)处产生的磁感应强度为[21]

保持伤口敷料清洁干燥,植皮患者植皮区制动,观察皮瓣的颜色、肿胀、弹性,综合判定皮瓣血运情况,发现异常及时报告主管医生[4]。

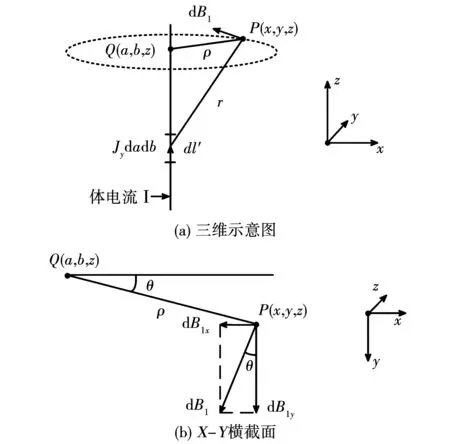
图3 电流元空间磁场示意图Fig.3 Schematic view of current element space magnetic field

因此，x反方向磁化单体模块在空间产生磁场为：

(1)

式中：μ0为真空磁导率；dl′为z方向导线的长度微元；r为长度微元dl′指向点P(x,y,z)的长度；ρ为点P(x,y,z)到导线垂点Q(a,b,z)的长度。

通过调节每个波位波束驻留时间来控制天线扫描速度，在雷达发射脉冲重复频率(PRF)已知的情况下设计每个波位的脉冲计数，当前波位脉冲计数积累到一定值N时，波束扫描一个步进，根据定点聚束模式几何关系，为保证波束在地面照射区域的移动速度为0，波束扫描速度与飞机平台运动速度持恒，其波位脉冲驻留数计算公式如下：

(2)

联立式(1)和式(2)，用坐标(a,b,z)和(x,y,z)表示sinθ和cosθ，积分可得体电流I在空间产生的磁场为：

(3)

同理，可求得体电流II、III、IV在空间所产生的磁场分别为：

(4)

其中：

(5)

(6)

(7)

根据文献[14]，利用面电流法，其永磁体在空间产生的磁场可等效为4个面电流在空间所产生磁场的叠加，设永磁体y方向磁化时的等效面密度为Ky，可求得4个面电流在空间产生的磁场为：

(8)

因此，y方向磁化单体模块在空间产生的磁场为：

(9)

2.2 X反方向磁化

一女生率直地说我的口语不好，我感到震惊和感激。The pressure ends up to be driving force. I should treasure and carefully store it in my mind(2004年9月9日)

图4 X反方向磁化单体模块Fig.4 X reverse direction magnetization monomer module

同理，可求得体电流V、VI、VII、VIII在空间产生的磁场分别为：

(10)

(11)

(12)

(13)

同理，基于文献[14]的理论推导，利用面电流法，设永磁体x反方向磁化时的等效面密度为Kx，可以求得其永磁体在空间产生的磁场为：

(14)

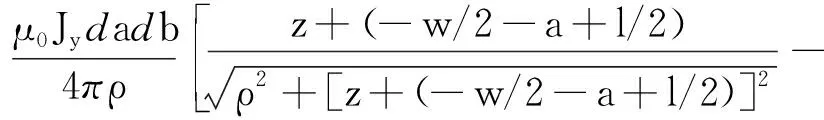
2.2.4.3 发病条件。病原菌以菌丝或分生孢子在脱落病叶上的分生孢子器中越冬。次年春季牧草返青后遇到适宜的温湿度条件，即可侵染植株下部叶片，后通过田间多次再侵染，病害逐渐向植株上部蔓延。

(15)

2.3 空间磁场计算

图1中永磁电磁混合Halbach阵列所取参考坐标原点位于第一个模块下表面正中心，而式(3)～式(15)所求磁场参考坐标原点皆为模块内部中心点处。因此，需利用坐标平移方法将式(3)～式(15)所求磁场转换到图1中参考坐标系下，坐标转换如图5所示。

图5 磁场坐标转换Fig.5 Magnetic field coordinate transformation

图5中，向量a((n-1)h,-h/2)为阵列坐标原点指向各模块中心的矢量，则有：

(16)

式中n为阵列第n块模块。

将式(16)代入到式(3)～式(15)中进行坐标转换后，再结合叠加原理，可求得永磁电磁混合Halbach阵列所有模块在空间任意位置产生的磁场为

h/2,Jy(φn),Ky(φn)]+

由于内部审计涉及的营销、财务等多个业务，所以本文针对以红河建水居民用电量为例子使用R语言实现k-means算法进行分析，来体现聚类算法在内部审计中的应用。具体实现流程如下。

Bsf[x′-(n-1)h,y′+

h/2,Jx(φn),Kx(φn)]}。

(17)

式中f=x、y、z，Bvf和Bsf可分别由式(9)及式(15)得到。N为模块数量，φn为第n块模块磁化方向与+y方向的夹角，且有：

(18)

式中：J为有源线圈体电流密度；m为Halbach阵列一个周期所含模块数量。

3 有限元法仿真验证

为了对所推导的永磁电磁混合Halbach阵列空间磁场解析表达式的正确性进行验证，采用ANSYS Maxwell有限元软件建立3D有限元模型[22]，模型参数见表1。3D模型线圈材料采用铜材，相邻线圈之间设置绝缘边界条件，以空气包围整个求解域，最外层边界采用自然边界条件，手动划分网格，得到的3D有限元模型及磁密矢量图分别如图6及图7所示。从图7可以看出，磁场主要集中于阵列下表面，上表面磁场得到很大削弱。

图6 3D有限元模型Fig.6 3D FEM

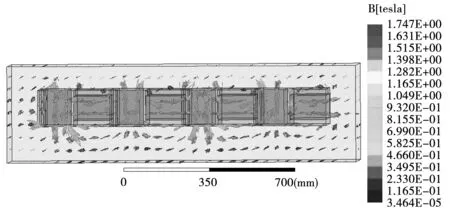
图7 永磁电磁混合Halbach阵列磁密矢量图Fig.7 3D magnetic flux density vector diagram

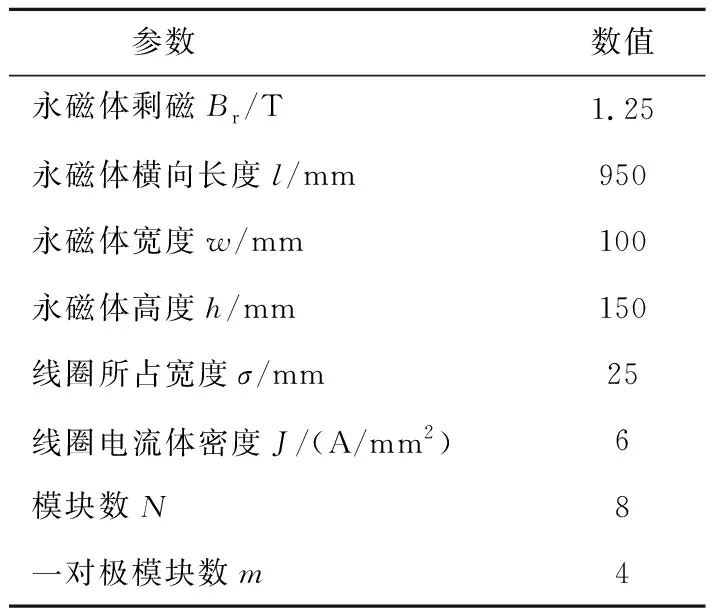
表1 永磁电磁混合Halbach阵列参数

相比于永磁Halbach阵列，永磁电磁混合Halbach阵列所特有的两个变量为线圈电流密度J和线圈所占宽度σ。结合表1参数，选取Bx分量作为研究对象。设阵列模块边长h恒为150 mm，气隙g=50 mm，z=0。

2) 阀门关闭时，所有压力全部作用在平衡密封环上，而密封环由VI-PTFE/EPDM /PTFE等非金属材料制成，由于软密封材料不耐高温， 一般低于200 ℃，在阀体内容易损坏，从而导致阀门泄漏。

3.2 定量评价 坎布拉国家地质公园的景观资源总体空间分布表现为：西部、南部是茂密的原始森林景观，南部森林线下的草原上分布着6个纯藏族自然村；北部、东北部是国家重点水电工程李家峡水库；中部是丹霞地貌分布区，且分布有藏传佛教寺院等宗教文化景观。据此，将坎布拉地质公园划分为丹霞地貌景观区、原始森林景观区、李家峡水库景观区。

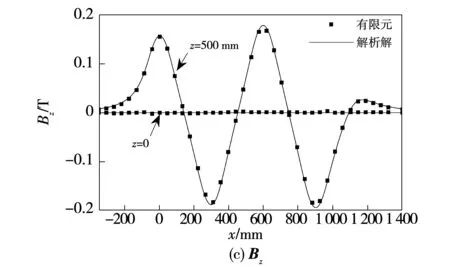
图8 空间磁场解析计算与有限元法结果对比(y=50 mm)Fig.8 Comparison of analytic and FEM(y=50 mm)

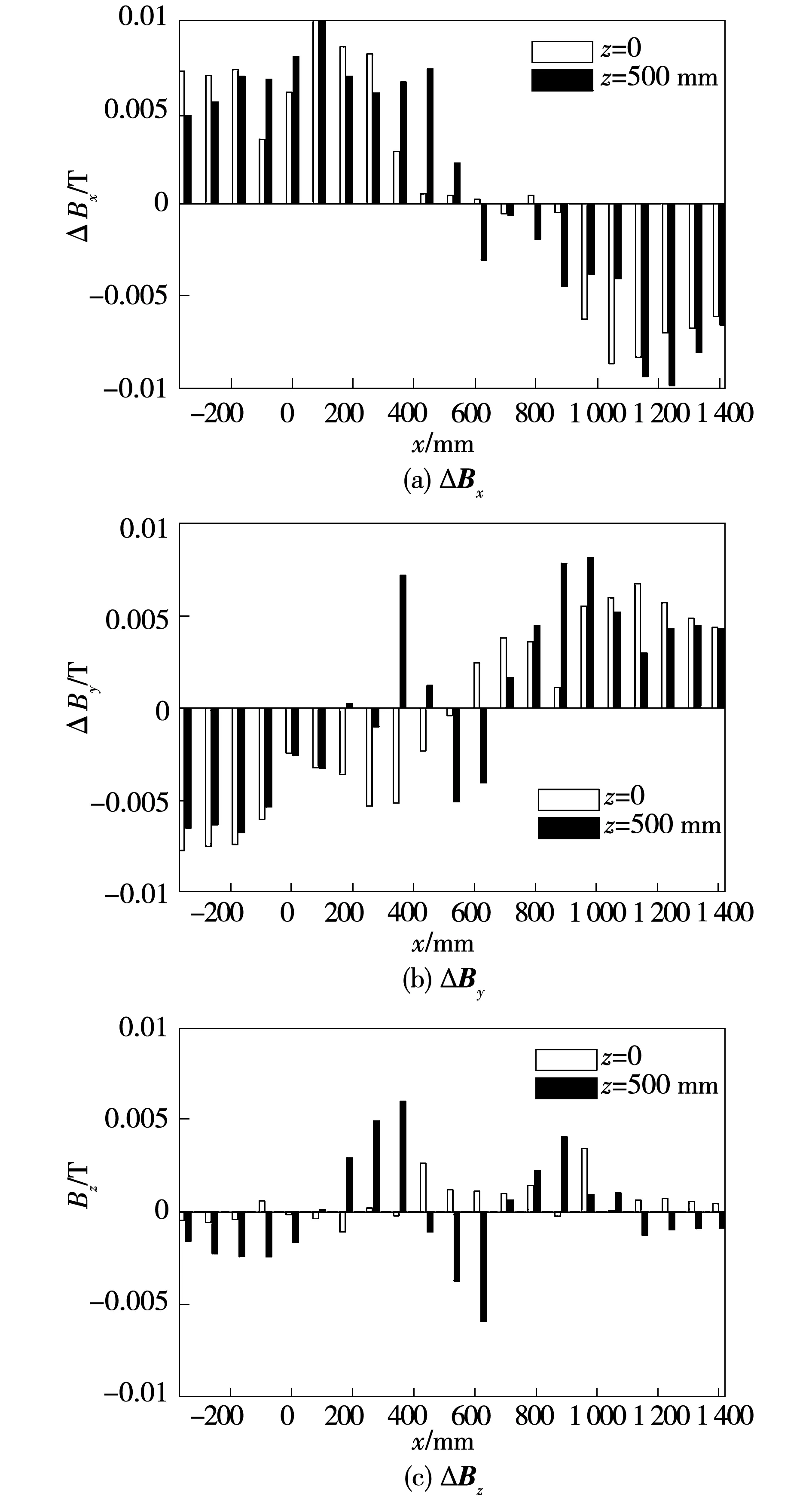
图9 解析解与有限元绝对误差(y=50 mm)Fig.9 Absolute error between the analytic and FEM(y=50 mm)

4 参数分析

空间磁场的解析计算与有限元分析结果对比及二者绝对误差分别如图8、图9所示。由图8和图9可见，磁场解析计算结果与有限元仿真结果吻合良好，其x、y、z分量磁场最大绝对误差值仅分别为0.01、0.008、0.006 T，验证了所推导空间磁场解析表达式的正确性。且该解析表达式考虑了端部效应，纠正了将永磁Halbach阵列视为理想结构，空间磁场近似为正弦磁场所带来的误差，精度更高。随着z方向位移的增大，磁场x、y分量将减小，z分量增大，在磁体横向中心(z=0)处，Bx、By取得最大值，Bz取得最小值。

4.1 线圈所占宽度σ对磁场的影响

设永磁体单独构成的永磁Halbach阵列x分量磁场幅值为Bxm_PM，永磁电磁混合Halbach阵列x分量磁场幅值为Bxm，则不同电流密度作用下Bxm/Bxm_PM与2σ/h的关系曲线如图10所示。

图10 混合Halbach阵列与永磁Halbach阵列空间磁场之比随2σ/h的变化关系Fig.10 Magnetic field comparison between hybrid Halbach array and PM Halbach array with coil width

由图10可见，随着线圈所占宽度的增加，空间磁场幅值近似成线性减小，当J=0时，在2σ=0.2h和2σ=0.3h处(图10中“*”标注点)，Bxm分别为0.77Bxm_PM和0.66Bxm_PM。

4.2 电流密度J对磁场的影响

图11为不同线圈宽度，永磁电磁混合Halbach阵列空间磁场x分量幅值Bxm与永磁Halbach阵列x分量幅值Bxm_PM之比随电流密度J的变化曲线。

由图11可见，当J从-6 A/mm2变化到6 A/mm2时，永磁电磁混合Halbach阵列磁场近似线性增大，且越接近于永磁Halbach阵列磁场幅值。

传统初中英语阅读教学往往是教师指定阅读对象，学生主体性体现有限，不能体现个性化发展，学生阅读兴趣也难以得到提高。面对这一教学问题，教师可以将阅读学习开放化，除教材必修内容外，鼓励学生自己寻找阅读材料，可以是互联网上的新闻，可以是好的英文文章，甚至可以是电影字幕，只要落到实处，达到阅读学习目的即可。通过如此开放化的阅读学习方式，学生学习积极性能够得到进一步解放，从而实现教学有效性的提高。

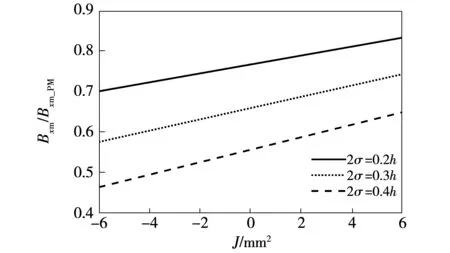
图11 混合Halbach阵列与永磁Halbach阵列空间磁场之比随电流的变化关系Fig.11 Magnetic field comparison between hybrid Halbach array and PM Halbach array with current density

4.3 电流密度J对磁场的调节性能

永磁电磁混合Halbach阵列x分量磁场幅值Bxm与其Bxm0(J=0)之比随电流密度J的变化关系曲线如图12所示。

由图12可见，永磁电磁混合Halbach阵列空间磁场可通过线圈电流对其进行调节控制。随着电流密度的增加，永磁电磁混合Halbach阵列空间磁场幅值近似线性增大，且随着线圈宽度的增加，线圈电流对磁场的调节范围越大。在2σ=0.2h和2σ=0.3h条件下，当电流密度J从-6 A/mm2变化到6 A/mm2时，磁场幅值Bxm约为Bxm0的0.91～1.09倍和0.87～1.13倍。

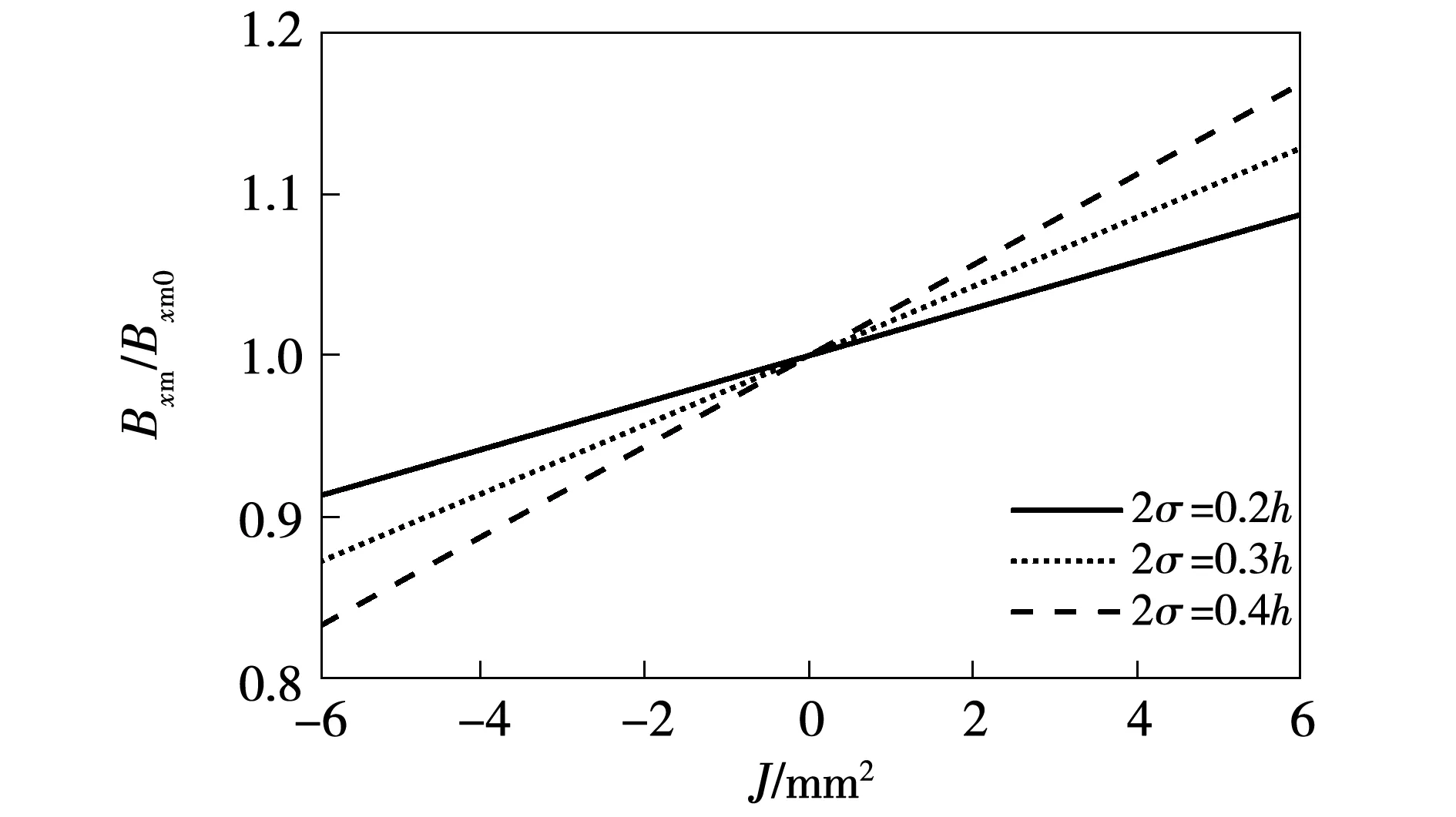
图12 线圈电流J对空间磁场的调节性能Fig.12 Adjustment performance of magnetic field with current density

5 结 论

本文针对永磁电动悬浮系统Halbach阵列空间磁场不可控，研究了一种永磁电磁混合Halbach阵列，其可通过永磁体表面线圈电流对Halbach阵列空间磁场进行主动调节控制。首先对永磁电磁混合Halbach阵列空间3D磁场解析表达式进行了推导。然后通过建立3D有限元模型，验证了解析表达式的正确性。最后，分析了线圈所占宽度、线圈电流密度对空间磁场的影响。分析表明，当线圈电流密度J从-6 A/mm2变化到6 A/mm2时，随着线圈宽度的减小或电流密度的增大，永磁电磁混合Halbach阵列空间磁场幅值Bxm近似成线性增大，且越来越接近于永磁Habach阵列空间磁场幅值Bxm_PM。同时线圈电流可对空间磁场进行调节，且调节范围随线圈宽度的增大而增大。当电流密度J从-6 A/mm2变化到6 A/mm2时，在2σ=0.2h和2σ=0.3h条件下，磁场幅值Bxm约为Bxm0(J=0)的0.91～1.09倍和0.87～1.13倍。本文所研究的永磁电磁混合Halbach阵列，结构简单，空间磁场计算方便，磁场调节范围较大。磁场解析表达式推导严密，结果准确，为后续永磁电动悬浮系统悬浮控制进一步的研究具有重要意义。