利用定义证明函数极限的教学体会

郭家勇

（江苏连云港师范高等专科学校 数学与信息工程学院，江苏 连云港 222006）

函数极限是微积分中一个重要的概念，它是微积分学的工具，微积分后面很多的概念都是通过函数极限来定义的，因此，掌握好函数极限这个工具在学习微积分中起到了至关重要的作用。而给出函数极限的定义也是经过了长期漫长的工作，最终由魏尔斯特拉斯给出了ε-δ定义。由于大多数微积分的教材都是先从函数极限定义开始讲起，而极限的ε-δ定义又比较抽象，很多初学者在刚开始学习时感到困难，对极限的定义理解不够深入，从而导致影响下面的学习。

这种情况一方面是由于大多数学生仅仅停留在中学数学的思维上，对极限这一新的概念没有真正理解它的含义；另一方面，很多教材过多地强调了极限抽象理论而忽略了直观认识。由于对函数极限的定义理解不够透彻，从而导致了用定义证明函数极限很多学生感到了困难，针对这种情况很多微积分教材也逐渐淡化这方面的内容，对用定义证明函数极限不做过多的要求，其实利用极限的定义证明函数极限一方面是我们讨论极限的一个重要的工具，很多重要的极限都是用极限的ε-δ定义证明给出的；另一方面，利用定义来证明函数极限也有助于学生加深对极限的ε-δ定义的理解。

一、函数极限ε-δ定义的理解

用定义证明函数极限首先要理解极限的定义，即若∀ε＞0，∃δ＞0，当0＜|x-x0|＜δ时，总有|f(x)-A|＜ε称函数f(x)在x0处的极限为A，记为这个定义的直观描述就是当x无限趋近于x0时，f(x)无限的趋近于A，也就是当x在x0某一个空心领域时，函数f(x)与A的距离比任意小的正数还要小。对于理解函数的ε-δ定义需要注意以下几点

1.x→x0指的是x无限趋近于x0而不等于x0，所以x接近于x0的领域是空心领域。

2.∀ε＞0，指的是任意小的正数，2ε，ε2，都可以表示任意小的正数。

3.当x无限趋近于x0时，x在x0的小空心领域内接近于x0，因此可以假定x在x0的某个空心领域内，比如可假设0＜|x-x0|＜1，或者等。

二、通过解不等式求出δ证明函数极限

利用函数极限的ε-δ定义证明函数极限关键是找δ，而如何找δ主要是通过∀ε＞0，要使不等式|f(x)-A|＜ε成立，解出需要|x-x0|＜δ(ε)，从而找出δ，这也是用定义证明函数极限的最基本方法。

证明∀ε＞0，要使不等式|2x+4-6|=|2x-2|=2|x-1|＜ε

三、通过不等式将|f(x)-A|放大求出δ证明函数极限

很多时候|f(x)-A|＜ε直接解不等式难以直接求出|x-x0|＜δ(ε)，

这时候我们往往可以先将|f(x)-A|用不等式放大，使得|f(x)-A|＜g(x-x0)＜ε，从而解出|x-x0|＜δ(ε)，在放大的时候要注意两点

2.g(x-x0)=0这个式子要比较简单使得g(x-x0)=0＜ε能够比较容易的解出|x-x0|＜δ(ε)。

证明∀ε＞0，要使不等式

四、假设|x-x0|＜δ1（常数）

由于x→x0指的是x在x0的空心领域内无限的趋近于x0，因此，在用定义证明函数极限时，可以先假设x在x0某个的空心领域内，即设0＜|x-x0|＜δ1（常数），其中常数δ1可以是任意的正的常数。从而利用这种方法便于将不等式放大。

证明∀ε＞0，|x2-4x+4-1|=|(x-1)(x-3)|，设0＜|x-3|＜1，

从而|x2-4x+4-1|=|x-3+2|(|x-3|)≤(|x-3|+2)|x-3|≤3|x-3|＜ε

五、设δ小于某个正数

由于δ表示任意小的正数，因此，在证明过程中我们可以假设δ小于某个正数，从而便于我们证明。

证明 ∀ε＞0，设x＞0要使不等式

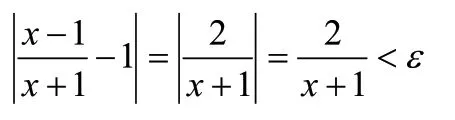
成立，设0＜ε＜2，解得x＞-1＞0。从而取M=-1＞0，则∀ε＞0，∃M=-1＞0，当x＞M时，总有＜ε，所以