基于机理分析法建立数学模型解决实际问题——6.9二元一次方程组及其解法

付慧玲

（上海市静安区实验中学，上海 200000）

众所周知，机理分析法是通过对系统内部原因（机理）的分析研究，从而找出其发展变化规律的一种科学研究方法，机理分析法立足于揭示事物内在的规律。建立数学模型[1]对现实情境问题进行数学抽象，用数学语言表达问题、用数学方法构建模型解决实际问题[2]；在初中阶段可以通过用代数式、方程、不等式、函数等表述数量关系的，体会模型的思想，建立符号意识。建立数学模型是一种数学的思考方法，也是运用数学符号语言与方法通过抽象、构建能解决实际问题的一种数学手段。

一、在教学的过程中确定问题的本质，探寻知识间的联系

例如，在学习上海教育出版社九年义务教育课本6.9二元一次方程组及其解法的过程中，开始有一个实际问题，中国古代的《孙子算经》中记载了一个有趣的鸡兔同笼问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何？”

我们将此问题抽象为两个数学等量关系，设笼中有鸡有x只，兔有y只，根据题意，得：

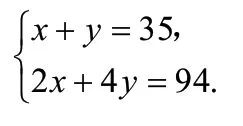
该实际问题的用途是为了引出二元一次方程组的概念及其解法。在本节课中，我们完成了具体的既定要求的教学目标，但其实我们可以继续思考学习，继续研究，假设这里的系数分别为a1,1b,c1,a2,b2,c2，那么我们就可以得到一个一般的二元一次方程组，从而建立了一个二元一次方程组模型：不难发现，该模型不仅仅可以解决“鸡兔同笼”问题，也可以解决“鸡鸭同笼”等“某某同笼”问题，同样可以解决“物品价格”以及“班级人数”等两个等量关系的问题，如下面三个问题：

问题1、参观上海科技馆的成人票、学生票分别为60元、45元。一天、科技馆卖出成人票、学生票共1万张，票务收入为51万元，问这两种票各售出多少张？

解：设售出成人票x万张，学生票y万张根据题意，得

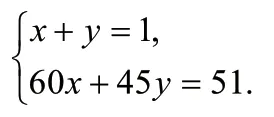
问题2、甲、乙两件商品按原价售出可得营业额140元，因季节原因，甲商品提价20%，乙商品降价20%，售出后的营业额比原标价少4元。问甲商品提价多少元？乙商品降价多少元？

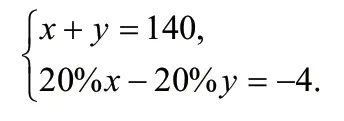
解：设甲商品原报价x元，乙商品原标价y元，根据题意，得问题3、六年级（1）班、（2）班各有44人，两个班都有一些同学参加课外天文小组。（1）班参加的人数恰好是（2）班没有参加的人数的；（2）班参加的人数恰好是（1）班没有参加的人数的。问六年级（1）、（2）班没有参加天文小组的各有多少人。

解：设六年级（1）班没有参加天文小组的有x人，（2）班没有参加的有y人，根据题意，得

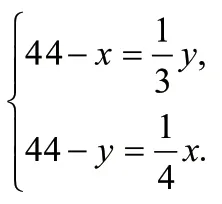
不难发现，以上几个问题所列的方程组只有系数不同而已。

二、关注学生的认知水平、注重知识间的螺旋上升

继续螺旋上升，在一次函数的应用中该模型的解就是两个一次函数的交点，这样问题就从数转化到了图形的问题上，由数到形的转化是知识难度的提高，也是学生认知水平的提升。我们知道图形的交点在视觉上是直观的，而如何求解在刚接触的时候稍有困难，那么教师就可以引导学生探寻问题的本质：联立两个一次函数的表达式，把求两个一次函数交点的问题就转化为了旧知识—求解二元一次方程组的解。如下面的问题：

问题1、如图，在平面直角坐标系中，一次函数y=2x-1与一次函数y=5-x相交于点B（2，3）；解二元一次方程组的解为

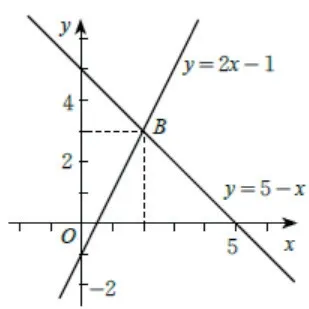
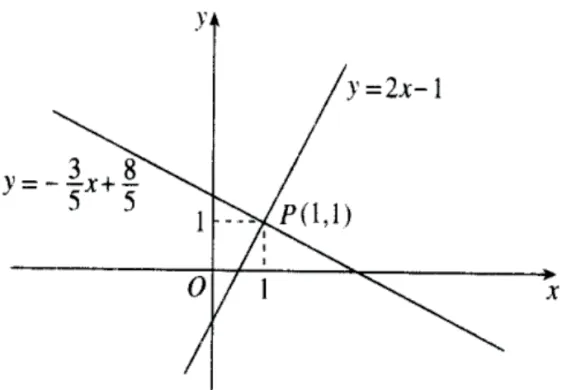
通过对二元一次方程组模型的认识学习，在熟知模型后，学生在预备年级不用被看似复杂的实际问题蒙蔽双眼、阻碍前行的道路，让他们有足够的信心解决求两个等量关系的实际问题，同时帮助他们避免深陷题海的泥潭；一个模型的学习不仅仅是着眼于解决当下遇到的实际问题，它也可以应用到之后求两个一次函数图像的交点问题。在这样一个过程中教师的教学有助学生知识建构；在学习的过程中学生也完善了自我的知识体系。

三、渗透学习知识的类比方法，培养知识迁移的能力

二元一次方程组模型的学习方法可以类比到一元二次方程及一元二次函数的学习上，也就是说学生学习的知识是不同的，但是学习知识的方法可以类比，注重知识与知识之间的类比能够加深对数学知识和方式方法的理解和掌握，更深层次的理解数学知识。建立数学模型[3]的目标比较明确，在教学过程中能够有效地降低教学的难度；建立数学模型[4]除了能够解决抽象化的问题，还能够引导学生完善自身基础知识的掌握程度，从而帮助学生知识体系建构[5]，促使学生提升创新力和逻辑推理能力，同时能够培养知识的迁移能力。

运用机理分析法建立数学模型是实现用数学知识解决实际问题的基础，对初中阶段的学生而言起点较低，掌握起来比较简单、快捷，同时也具有一定程度上的趣味性；在教学的过程中，运用机理分析法探索数量之间的关系，深入研究等量关系之间的实际意义，加以适当的延伸，渗透符号意识，加深模型印象，帮助学生摆脱题海战术的漩涡，树立解决实际问题的信心。