基于机器学习的算法设计研究

林泓斌 李佳莲

（广州大学数学与信息科学学院，广东 广州 511400）

引言

机器学习算法作为AI领域的重要分支，将其应用于智能系统中能够有效提升经验学习过程中的算法性能，为机器执行各项任务、辅助决策制定等功能实现提供支持。成绩评估预测是衡量学生学习效果与自我效能感的重要尺度，通过运用算法建立预测模型，能够为学习者考试成绩预测及决策制定提供重要支持。

一、典型机器学习算法

1.线性判别分析

线性回归算法主要适用于针对连续变量进行建模，对其变化结果进行预测。线性回归作为一种基础回归形式，通常借助直线拟合数据集，依托变量间的线性关系保障提高成功率，在数据分析和预处理上呈现出良好性能优势，可实现对学习数据的简化。作为线性回归算法中的重要分支，线性判别分析算法常应用于数据降维，再将多种数据分类后提炼出其中不同类数据的差异，增强不同类对象或事件间的分离性，在考试成绩预测、产品销售业绩评估等方面具备较强适用性[1]。

2.支持向量机

该算法常被应用于处理回归、分类等问题，通过寻找分类超平面作为决策边界，将位于同一组内的不同类对象分离，能够在训练数据集中筛选出正确的类别对象[2]。设样本集为{(x,y)|x∈Rn,yi=±1,i=1,2,...,l}，将分类超平面的法向量设为ω、截距为b、松弛变量为ζi、惩罚系数为C，则可将分类超平面定义为：

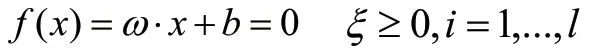
在运用该算法建立学习模型时，首要前提是定义最优分类面，引入软间隔或核函数实现对线性不可分及非线性问题的解决，在文本分类、面部识别等领域具备良好应用价值。

二、基于线性判别分析与支持向量机的考试成绩预测算法设计

1.算法原理

选取某学校毕业生的期中、期末课程考试成绩与升学考试成绩作为数据集，从中筛选出主要课程作为特征向量，基于随机森林进行重要性等级的排序，将其中非重要课程成绩剔除，实现学习模型训练特征维度的精简化处理。随后运用线性判别分析方法进行数据降维，以选定的直线为基准对训练集进行重复投影，划分出投影点的类别，并根据投影点所处的具体位置进行类别判断，可最大限度增加类间差异、缩小类内差异。接下来运用支持向量机建立考试成绩预测模型，为最终预测结果精度提供保障。

2.模型建立

将线性判别分析与支持向量机两种算法进行组合使用，分别利用两种算法在降维和分类上体现出的优势性能，提升考试成绩预测结果的精确性。在算法流程设计上，首先运用线性判别分析方法进行数据预处理，在此过程中将数据集导入系统中，完成训练集、测试集的划分，将其中的数据集进行标准化处理，并实行特征降维；随后建立支持向量机模型，待完成训练后进行样本测试，针对整体组合算法的实际应用性能进行评估。

3.实验结果分析

运用线性判别分析方法进行数据降维处理，判断各维度对于后续采用支持向量机算法获取到分类结果的影响，用于衡量在预测结果精确度最高时的降维维度。从中可以观察到，当降维维度为2时，支持向量机的分类准确度达到最优水平。

运用核函数进行非线性问题的处理，首先，采用径向基核函数，已知真实标签的第1—10个预测结果表示为[0000010011]，预测第1—10个结果表示为[0000000000]，在采用支持向量机进行毕业生升学考试结果预测后，可知0、1对应的precision值为0.77和0；avg/total值为0.59；recall值分别为1.0和0；avg/total值为0.77；fl-score值分别为0.87和0，avg/total值为0.67；support值分别为50和15；avg/total值为65。

其次，采用Linear Kernel线性核函数，已知真实标签的第1—10个预测结果，预测前10个结果表示为[0000000001]，基于支持向量机算法进行学生升学成绩的预测，可知0、1对应的precision值为0.82和0.5，avg/total值为0.74；recall值分别为0.9和0.33，avg/total值为0.77；fl-score值分别为0.86和0.4，avg/total值为0.75；support值分别为50和15，avg/total值为65。

再次，采用多项式核函数，已知真实标签的第1—10个预测结果表示不变，则预测出的前10个结果表示为[0000000011]，运用支持向量机算法进行升学成绩预测，可知0、1对应的precision值为0.84和0.45，avg/total值为0.76；recall值分别为0.79和0.54，avg/total值为0.74；fl-score值分别为0.83和0.47，avg/total值为0.75；support值分别为50和15，avg/total值为65。

最后，将上面三种核函数的分类报告结果进行比较，可以看出，采用Linear Kernel线性核函数和多项式核函数测得的F值高于径向基核函数，其中多项式核函数的预测结果精度相对更高，因此，宜选用多项式核函数建立支持向量机模型，为最终算法预测结果的精确度提供保障。

结语

机器学习算法在执行任务的过程中不断积累学习经验、改善应用性能，根据获取到的数据结果做出科学决策，最终保证任务的顺利完成。通过将两种典型算法应用于考试成绩预测模型设计中，可有效将学习者成绩汇总并对其顺利通过考试的可能性做出科学评判，保证预测结果的准确性，具备良好实用价值。