基于混沌信号时域波形包络特征的触电电流检测方法

石 砦，李春兰，王长云，夏兰兰，任 鹏

(1.新疆农业大学 机电工程学院，新疆 乌鲁木齐 830052；2.国网新疆电力有限公司 昌吉供电公司，新疆 昌吉 831100)

由于受到安装场所等外界干扰因素的影响，农村电网安全运行必不可少的剩余电流保护装置仍普遍存在误动作及投运率低等问题，导致因漏电引起的火灾甚至人身触电伤亡事故.这主要是由于目前常用的末级剩余电流保护装置是以剩余电流作为动作物理量，无法真正辨识出生物体触电支路的汲出电流，因而无法消除剩余电流保护装置的保护死区.

为了获得理想的触电保护特性，需从剩余电流中分离出触电电流.关海鸥等[1]利用基于偏度、峭度及信息熵等高阶统计量的方法，定量描述触电信号时间序列的数字特征信息，获得生物触电故障过程中数字特征的整体变化规律.LIU Y.M.等[2]采用AdaBoost算法及改进的支持向量机相结合的方法，建立了触电故障类型(植物触电故障、动物直接触电故障和动物间接触电故障)识别模型.但是上述文献均未涉及到触电电流信号分离问题.关海鸥等[3]、韩晓慧等[4]分别运用径向基神经网络及最小二乘支持向量机相结合的方法，建立触电电流检测模型，所提议的触电电流识别方法在构建网络模型时，均需要选取合适的网络结构和参数，需要大量的数据来训练模型.关海鸥等[5]利用希尔伯特-黄变换的自适应性对触电电流幅值进行检测，能有效检测触电电流的幅值，但算法对不同触电时刻触电电流的提取需要进一步验证.

近年来，混沌理论在电力系统故障定位、谐波检测及负荷预测等方面得到广泛应用[6-7].混沌系统从混沌状态到大尺度周期状态的分岔行为具有对小信号敏感和对噪声免疫的特性，使得混沌检测强噪声背景下的弱信号具有独特优势.李春兰等[8]提出了以最大李雅普诺夫指数作为判断混沌系统相变量化依据的混沌系统触电电流检测方法，但该方法存在求解李雅普诺夫指数时需相空间重构及计算复杂的缺陷.为此，李春兰等[9]进一步提出利用椭圆域分割与混沌理论相结合的方法检测触电电流，一定程度上解决了文献[8]存在的问题，但是对椭圆域长短轴的设定较为困难.在此背景下，笔者提出一种新的基于混沌信号时域波形包络特征的触电信号检测方法，用以解决对椭圆域长短轴设定较难的问题.

1 混沌系统检测弱信号原理

典型的混沌系统动力学模型有Duffing振子、Logistic 映射和Lorenz模型等.其中，Holmes 型Du-ffing振子在微弱信号检测领域应用较为广泛[10]，其方程通常被描述为

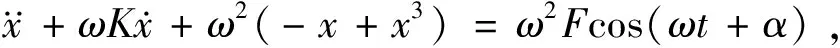
(1)

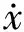
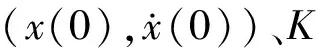
设待测信号s(t)为

s(t)=Acos(ωt+φ)+n(t)，

(2)

式中：A和φ分别为待测信号的幅值和初相位；n(t)为待测信号中包含的噪声.

为了简化后续的计算过程，取式(1)中的α=0°，则φ也为待测信号与混沌系统内置周期策动力两者的相位差.将s(t)作为新的策动力引入到处于临界状态的混沌系统中，其中，临界状态是指系统从混沌状态转变为大尺度周期状态的过渡状态，式(1)变为

s(t)]=ω2[F′cos(ωt+θ)+n(t)]，

(3)

式中：Fd为原始混沌系统临界状态对应的内置周期策动力幅值(临界状态仅对应一个确定的策动力幅值)；F′为总策动力幅值，即

(4)

θ为总策动力的相角，即

θ=arctan[Asinφ/(Fd+Acosφ)].

(5)

分析式(3)-(5)，考虑混沌系统对噪声有极强的免疫力，且Fd≫A，因此n(t)及θ可忽略不计.由式(4)可知，系统的状态不但与待测信号的幅值有关，还和待测信号与内置周期策动力间的相位差φ有关.总周期策动力可看作内置周期策动力与待测信号的矢量叠加，如图1所示.图中的Fk1与Fk2分别表示两种相位差情况下加入待测信号后，混沌系统重新回到临界状态所对应的内置周期策动力的幅值.

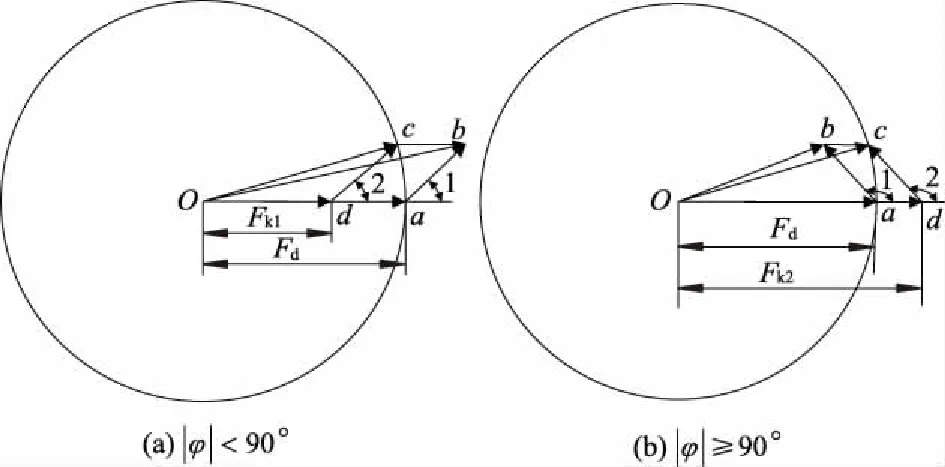
图1 总周期策动力矢量图

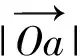
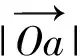
根据式(4)得

(6)

当待测信号与内置周期策动力同相位，即认为φ=0°时，检测值为

A0=Fd-Fk1，

(7)

则绝对误差为

e=|A-A0|.

(8)

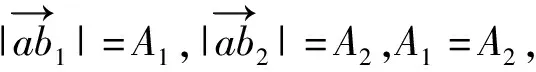
0°≤φ1<φ2<90°.

(9)

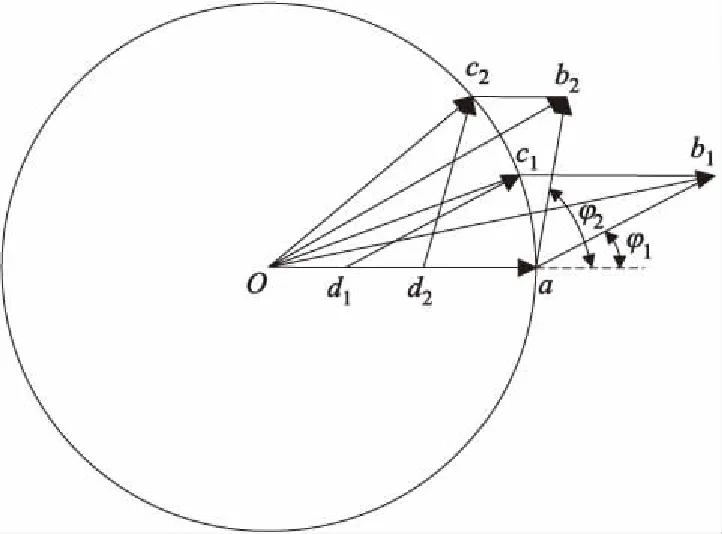
图2 幅值相同、相位不同的2个待测信号矢量图

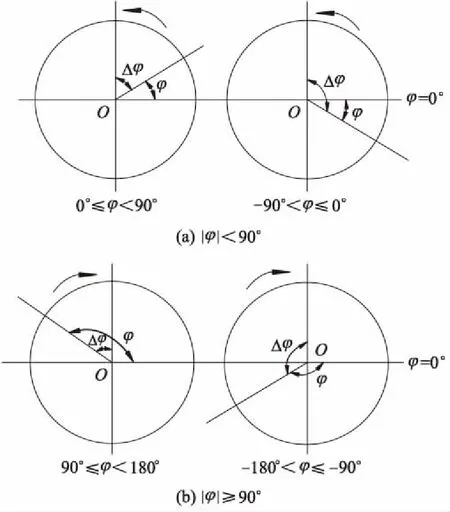
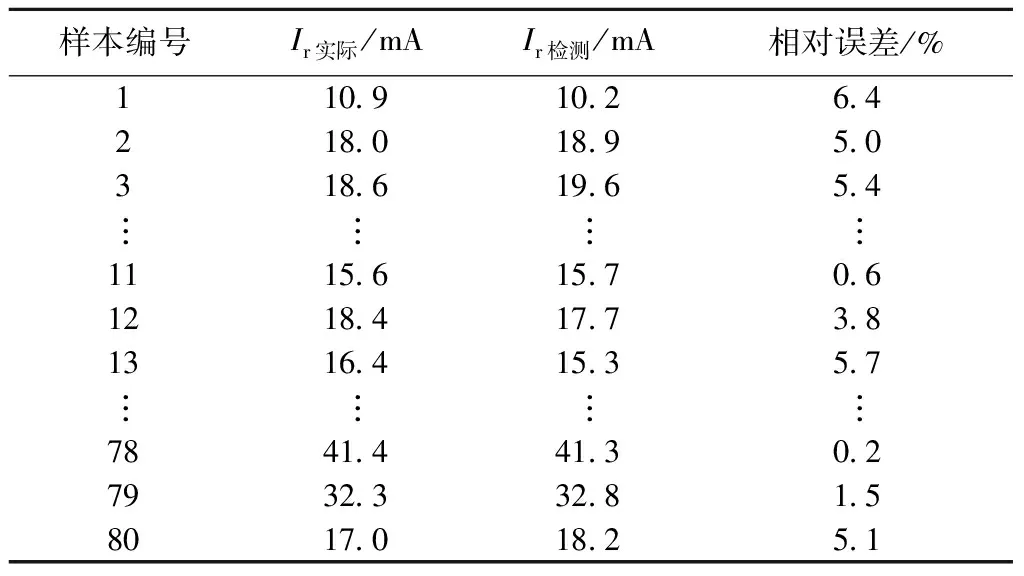
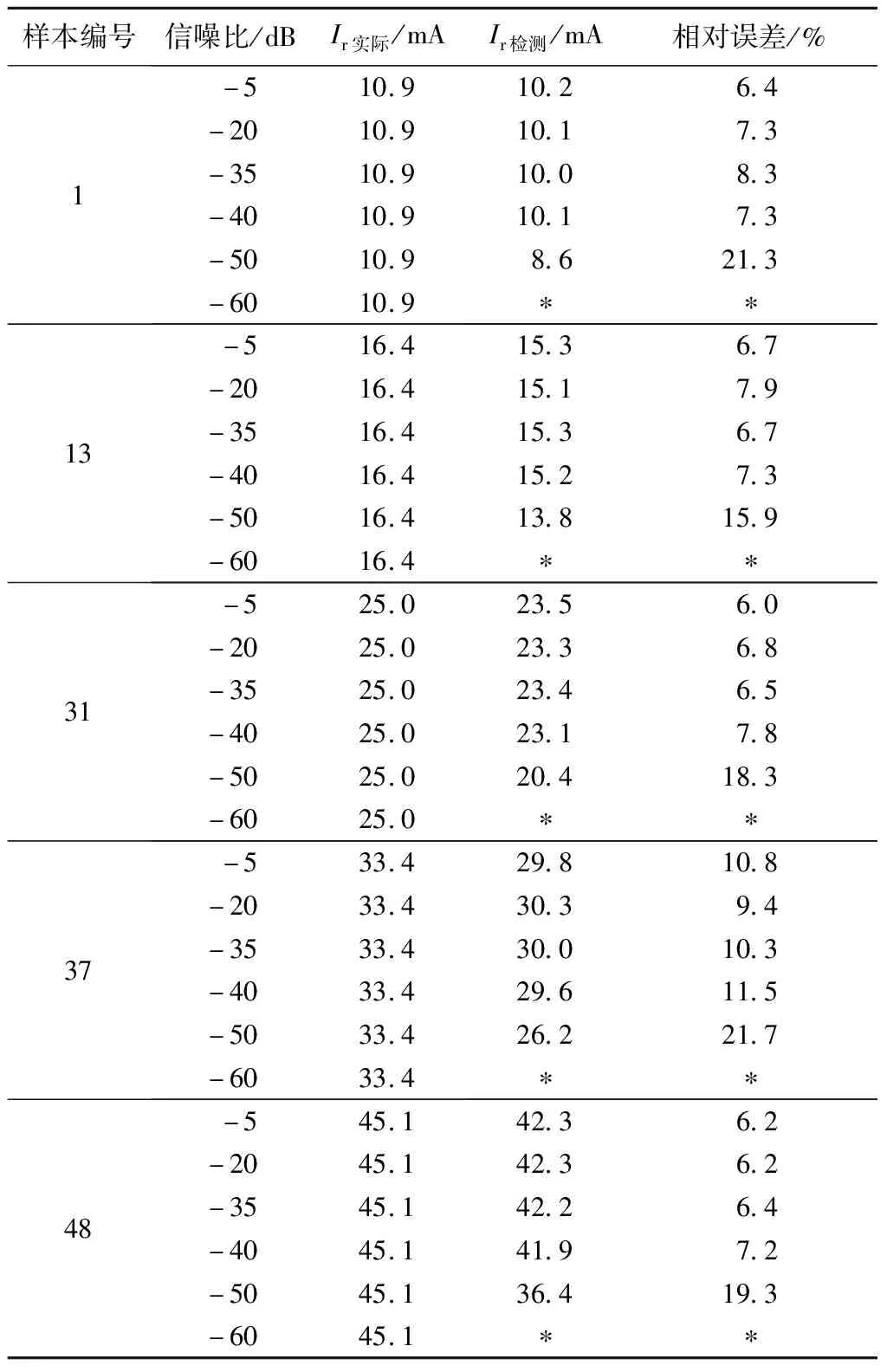
e1

(10)

由式(9)和(10)可知，待测信号与系统固有周期策动力的相位差会影响测量误差，当|φ|<90°时，误差随着|φ|的增加而增加.

根据式(4)得

(11)

当φ=180°，即待测信号与内置周期策动力相位相反时，有

A0=Fk2-Fd.

(12)

同理，可推得当|φ|≥90°时，测量误差随着|φ|的增加而减小.

综上所述，待测信号和系统固有周期策动力的相位差影响信号检测误差，当两者相位相同或相反时，信号检测误差最小.因此，为了减小信号检测误差，就需要检测出待测信号的初相位φ及Fk1(或Fk2).

2 基于混沌理论的待测信号相位检测

根据式(4)可知，处于临界状态的混沌系统加入待测信号后，欲使系统重新回到总策动力幅值F′=Fd的临界状态，除通过改变内置周期策动力幅值外，也可通过改变待测信号初相位来实现.待测信号初相位混沌检测方法如图3所示.图3中，将待测信号的初相位φ逆时针移相至图3a相位φ′或顺时针移相至图3b相位φ′处，则混沌系统重新回到临界混沌状态.

图3 待测信号初相位混沌检测方法矢量图

根据式(4)可以解得cosφ′=-A/(2Fd).由于A<

φ=90°-Δφ,|φ|<90°，

(13)

φ=90°+Δφ,|φ|≥90°，

(14)

式中：Δφ为将混沌系统调整至临界状态所需的待测信号相位调整量.

图4为系统状态和待测信号相位的关系示意图,其中左半圆平面为混沌状态，右半圆平面为大周期状态.

图4 系统状态和待测信号相位的关系示意图

提议的待测信号相位检测步骤如下：

1)将待测信号加入处于临界状态的混沌系统中，若系统发生正向相变，则待测信号初相位φ在(-90°,90°)范围内，执行步骤2)；若系统发生逆向相变，则待测信号初相位在[90°,180°)∪(-180°,-90°]范围内，执行步骤3).

2)将待测信号相位逆时针移相Δα，此时相位φm=φm-1+Δα，m∈[1,2,…)，相位增量Δφm=Δφm-1+Δα.若系统不是临界状态，重复步骤2).直到系统发生逆向相变，记录此时移相增量Δφm，见图4a，利用式(13)计算φ.

3)将待测信号相位顺时针移相Δα，此时相位φm=φm-1-Δα，相位增量Δφm=Δφm-1+Δα.若系统不是临界状态，重复步骤3)，直到系统发生正向相变，记录移相增量Δφm，见图4b，利用公式(14)计算φ.

3 基于x时域波形包络特征的触电信号检测

利用混沌理论检测待测信号幅值的关键在于混沌系统临界状态的正确判别.传统的求取Duffing系统临界阈值的方法有梅尔尼科夫法、李雅普诺夫指数法等[11-12]，存在计算复杂且计算量大等缺陷，鉴于此，笔者提出一种基于混沌信号x时域波形包络特征的状态求解方法.

3.1 状态迁移检测

Duffing振子在混沌状态和大周期状态下，混沌信号x时域波形如图5所示.

图5 混沌状态和大周期状态下的x时域波形

由图5可知：大周期状态下x时域波形的包络线近似为直线，其起伏远小于混沌状态；混沌状态对应复杂的运动轨迹，包络线波动较大，且无规律.据此可以区分系统的2种不同运动状态(即混沌状态和大周期状态).

混沌信号x的包络线为x时域波形正极大值点(或负极小值点)连接起来的曲线，而波形正极大值点(或负极小值点)的标准差能够反映该组数据集的离散程度，标准差越大，数据波动越大.因此，笔者以混沌系统输出x时域波形正极大值点或负极小值点的序列标准差V作为衡量x时域波形包络线波动情况的定量指标，即

V=max(σ1,σ2),

(15)

式中：σ1和σ2分别为混沌信号x时域波形上包络线极大值点序列Ci(i=1,2,…,n)的标准差和下包络线极小值点序列Bj(j=1,2,…,m′)的标准差.计算式如下：

(16)

(17)

提议的混沌系统状态迁移检测思路如下：

1)对系统输出的混沌信号x求微分，分别获得上包络线极大值点序列Ci(i=1,2,…,n)及下包络线极小值点序列Bj(j=1,2,…,m′)，Ci和Bj分别表示在时间数据窗内信号x的第i个极大值的幅值和第j个极小值的幅值.

3)利用式(16)、(17)分别计算σ1、σ2.

4)利用式(15)，求得V.若V>Vd(Vd为区分混沌状态与周期状态的临界值)，系统为混沌状态；V≤Vd，系统为大尺度周期状态.

3.2 状态迁移判据

图6中，S1、S2、S3和S4区域分别对应Duffing混沌系统同宿轨道(0 ≤F≤0.380 0)、倍周期分岔(0.380 00.953 5).由图6可知：①σ1、σ2值随策动力幅值F的改变而变化，在同一策动力幅值下，获得的σ1、σ2相互间数值大小关系随机；根据σ1、σ2值均能区分系统的状态.② 系统混沌状态和周期状态对应V值范围分别为[0.535 9，1.030 4]和[0.127 1，0.151 2]，可见两者所对应的V值范围明显不同.

图6 不同策动力下x时域波形极值标准差及V值曲线

根据式(15)，选取包络线变化判断阈值Vd=0.2，且在利用指标V值判断系统临界状态时，为避免V< 0.2 时系统处于同宿轨道情况，尽可能取较大的原始混沌系统初始策动力幅值，使系统初始状态不处于同宿轨道状态.

3.3 触电电流幅值检测

正常情况下，低压电网存在数值较小的剩余电流.当发生人身触电事故后，剩余电流为正常剩余电流与触电电流ir的矢量和，因此，触电电流ir为触电后与触电前的剩余电流矢量差.触电电流混沌检测方法矢量图如图7所示.

图7 触电电流混沌检测方法矢量图

Ar如下：

(18)

由前文可知，处于临界状态的混沌系统在加入待测信号后求取Fk1或Fk2时，需通过改变内置周期策动力幅值F实现；根据第2部分提议的相位检测步骤调整待测信号相位.因此，笔者提议用2个并列运行的混沌检测器检测待测信号.基于x时域波形包络特征的触电电流检测流程如图8所示.

图8 基于x时域波形包络特征的触电电流检测流程图

基于混沌信号x时域波形波动特征的触电电流检测步骤如下：

2)对混沌系统x时域信号输出进行采样，获得混沌系统x时间序列，由公式(15)和(17)计算序列标准差V.

3)若V<0.2，则用F=F-ΔF进行修正后，返回步骤2)，重新计算新策动力下的V，直到V≥0.2，输出此时的F，即为混沌系统临界状态的策动力幅值Fd.

4)将触电前、后剩余电流信号作为策动力，分别注入处于临界状态的原始Duffing系统，根据图8所示检测流程，分别获得触电前剩余电流的幅值Ak1、初相位φk1，以及触电后剩余电流的幅值Ak2、初相位φk2.

5)利用式(18)计算触电电流幅值Ar.

4 仿真分析

原始数据来源于课题组前期研究成果.以猪为试验对象，利用触电物理试验平台，通过故障录波器获取触电信号，故障录波器的采样频率为10 kHz.笔者选取80组试验数据作为检测样本，每组数据中包含电源电压(us)、瞬时剩余电流(iΔ)和瞬时触电电流(ir)，每种信号分别包含触电前、后4个周期各800个采样点数据.为验证检测方法的有效性，检测样本分别覆盖电源电压任意时刻、电源电压过零时刻和电源电压最大值时刻的触电样本数据，结果如图9所示.

图9 3种典型触电时刻触电原始信号

为了比较相位修正对检测结果的影响，统计出80组样本触电时刻初相位.样本编号与3种典型触电时刻的对应关系如表1所示.表2为提议检测方法的检测结果，其中Ir实际和Ir检测分别为触电电流的实际幅值和检测值.

表1 典型触电时刻与初相位的对应关系

表2 触电电流幅值检测结果

由表2计算可知：电源电压最大时刻、电源电压过零时刻和电源电压任意时刻触电的平均检测误差分别为6.40%、5.50%和2.03%；提议方法平均检测误差为4.64%；提议的混沌系统状态判据可准确判断系统周期状态和混沌状态.

为比较本小节提议方法的抗噪能力，选取20组数据的总剩余电流，分别增加噪声至信噪比为-5、-20、-35、-40、-50和-60 dB，并对加噪后的信号进行检测.表3为不同幅值和信噪比下触电电流信号检测结果.

表3 不同幅值和信噪比下触电电流信号检测结果

由表3可知：提议的算法适用的信噪比范围为[0,-50]dB；当噪声的信噪比为[-5,-40]dB时，不同噪声强度下，检测误差波动较小，且与不加入噪声情况下的检测误差较为接近，表明提议算法能够显著消除该信噪比范围内的噪声干扰；信噪比小于-40 dB时，检测误差显著增大；信噪比小于-60 dB时，因噪声占比过大，已无法提取有效信号.

5 结 论

1)根据混沌理论，利用矢量分析法，提出一种待测信号初相位混沌检测方法，用于减小幅值检测误差.

2)根据Duffing振子混沌状态输出x时域波形包络线的波动远大于周期状态的相应输出，将x时域波形极值点(极大值点或极小值点)序列的标准差V作为描述混沌信号时域波形包络线波动情况的指标，并选取包络线变化判断阈值Vd=0.2，定量判别系统临界状态，从而基于矢量分析法提出一种新的触电电流幅值检测方法.

3)基于提出的相位检测与幅值检测方法，对本课题组前期测得的动物(猪)物理触电试验信号进行仿真分析.提议方法平均检测误差为4.64%，且对所有试验信号都能准确判断系统周期状态和混沌状态，未出现误判现象.提议方法在信噪比为[0,-40]dB时均可保持可靠的检测精度，消除噪声干扰.