基于聚类提升树的多标签学习

王 进，余 薇，孙开伟，邓 欣

(重庆邮电大学 数据工程与可视计算重点实验室，重庆 400065)

多标签学习(multi-label learning, MLL)旨在为分配了多个类标签的对象构建分类模型[1].多标签学习广泛存在于现实世界的应用程序中：文本分类，一则新闻可以涵盖多个主题[2]，包括政治、经济和改革；多媒体内容注释，1个图像可以展示包括海滩和建筑在内的几个场景[3]；生物信息学，1个基因可以具有多种功能[4]，包括代谢、蛋白质合成和转录.

多标签学习算法应用已经取得了成功[1].由于每个类别的标签应该具有自己的特定特征，因此传统的方法并不是最理想的选择.例如，自动图像注释中，在区分天空和非天空图像时基于颜色的特征将是首选，在区分沙漠和非沙漠图像时基于纹理的特征将是首选，而颜色和纹理可能都是有助于区分标签空间中其他标签的首选特征.再比如，文本分类中，在区分经济和非经济文本时，与GDP、减税、股票市场等词汇相关的特征则具有相关性.由此可见，每个类别的标签均具有自己的特定特征，挖掘标签特定特征对多标签学习而言显得至关重要.处理多标签学习问题面临的核心挑战就是如何通过探索多个标签之间依赖关系来提高预测准确性，探索标签间相关性的一种直接方法是为扩展特征空间上的每个标签建立单独的分类模型，并将其他标签的预测值视为附加特征.这种策略简单直观，但它可能会因为训练集和预测集之间附加特征值的差异导致预测性能的一定退化.简言之，构建标签的特定特征以及挖掘样本之间的关联关系在多标签学习中都至关重要.

文献[5]首次提出了一种名为multi-label lear-ning with label specific features(LIFT)的特征转换新方法，该方法通过构建标签特定特征作为输入空间来处理多标签数据，计算每1个原始特征到每1个标签原始聚类簇中心的欧式距离，将获得的欧式距离映射为标签特定特征，挖掘样本内部聚类关联，但没有考虑标签相关性.随后，文献[6]提出一种名为learning label-specific features(LLSF)的方法，学习每个标签的标签特定特征，假设每个标签仅与给定数据集原始特征集中相关特征的子集相关联，这些相关特征可以视为标签特定特征，但LLSF没有寻找多标签样本之间的关联关系.文献[7]和[8]提出learning label-specific features and class-dependent labels(LLSF-DL)和regularization enriched label-specific features(REEL)两种基于标签特定特征的方法分别是对LLSF和LIFT算法的改进，具备更加明显的分类性能优势.文献[9]提出了一种称为label-specific features and local pairwise label correlation(LF-LPLC)的标签特定特征方法用于多标签学习，着重通过丰富标签的语义信息来解决不平衡的类分布问题.文献[10]设计了1个优化框架来学习特征的权重分配方案，并通过同时构建附加特征来考虑标签之间的相关性，但模型更加复杂，时间成本也更大.

受到文献[5-10]中基于标签特定特征工作的启发，文中着重进行对标签特定特征的学习与研究，提出了基于聚类提升树的多标签学习算法(multi-label leaning based on boosting clustering trees, MLL-BCT).MLL-BCT方法首先引入聚类特征树挖掘数据样本之间本身的相关性，再在新的样本集合上构建局部特征转换框架，利用梯度提升树构建标签特定特征.

MLL-BCT采用区别于现有成熟的标签特定特征算法(大多是基于LIFT和LLSF的改进)的特征构建方法，提出一种随机局部特征抽取框架，通过特定学习局部特征集合的梯度残差，为每个标签探索与该标签最具关联性的特定特征集合.

1 聚类提升树多标签分类模型

1.1 符号定义

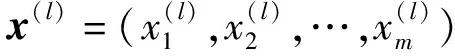
1.2 MLL-BCT算法框架

为了对多标签学习进行建模，探索出每个标签的有效特征，文中提出了基于聚类提升树的多标签学习算法MLL-BCT，算法框架包括以下两个阶段：

1)聚类特征树：原始数据集使用CF-Tree方法进行聚类，挖掘样本之间的关联关系，当样本聚类为1个类别时，认定输出空间具有紧密的相关性.

2)标签特定特征：根据随机局部特征转换方法为每个标签构建标签特定特征.需要根据随机局部特征转换构建初始模型，利用梯度提升分类树，计算出残差预测值，然后标签的残差预测值作为附加特征来拓展特征空间.

图1为MLL-BCT的训练与预测框架.

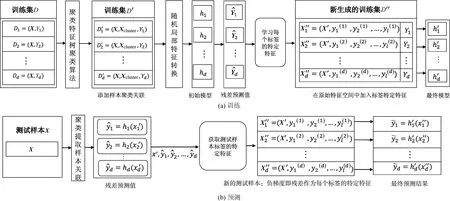
图1 MLL-BCT的训练与预测框架

如图1所示，在训练阶段，首先将训练集利用聚类特征树聚类算法挖掘样本之间的关系，聚类结果表征了样本在输出空间具有相似特征；然后利用随机局部特征转换框架，设置梯度提升树学习棵数，以及每次需要随机抽取的特征维数，将每个标签对应的若干梯度提升分类树的残差预测值作为标签特定特征，并作为附加特征添加到原始空间中，得到最终的模型.在测试阶段，与训练阶段相同，构建得到新的测试样本，输入模型获得最终预测的结果.

1.3 聚类特征树

1.3.1CF-Tree算法过程

聚类特征树即CF-Tree，树的每1个节点由若干个聚类特征(CF)组成，而每1个CF是1个三元组，可以用(N，LS，SS)表示，其中N、LS、SS分别代表了CF中样本点的数量、各特征维度的和向量、各特征维度的平方和.聚类特征树的每个节点包括叶子节点都有若干个CF，而内部节点的CF有指向孩子节点的指针，所有的叶子节点用1个双向链表链接起来.简言之，根据定义的CF三元组，通过计算三元组之间的距离阈值来判断是否吸收该元组从而构建1棵二叉树的CF-Tree.

构建好初始的CF三元组后，就可进行聚类特征树构建，也即是对样本的聚类过程，聚类特征树的伪代码见算法1.

首先，定义初始种子的计算式为

(1)

数据点到种子的距离计算式为

(2)

聚类簇内间元组的平均距离计算式为

(3)

算法1输入：数据集样本D；输出：聚类特征树模型T.其流程如下：

nroot←newNode

构造树模型(nroot)

T←nroot

返回 模型T

过程 构造树模型

输入样本D

阶段1 建立初始化的CF-Tree，把稠密数据分成簇，稀疏数据作为孤立点对待

阶段2 在阶段1的基础上，建立1个更小的CF-Tree

阶段3 使用全局算法对新建立的CF-Tree全部叶节点进行聚类

阶段4 使用阶段3的中心点作为新种子，重新分配数据点到新种子，添加簇类标签

返回 该过程

过程 根据式(1)构建CF-Tree

从根节点开始，自上而下选择最近的孩子节点

到达叶子节点后，检查最近的元组CFi能否吸收此数据点根据式(2)和(3)决定

if最近元组CFi可以吸收then

更新CF值

else判断是否可以添加1个新元组

if是then

添加1个新的元组

else

分裂最远的一对元组，作为种子，按最近距离重新分配其他元组

if是then

添加1个新的元组

else

分裂最远的一对元组，作为种子，按最近距离重新分配其他元组

end

end

更新非叶子节点的CF，直到root

返回 该过程

1.3.2应用CF-Tree挖掘多标签数据样本关联

文中通过应用无监督学习聚类特征树的方法来挖掘样本之间的关联，也即输出空间的相似性.如图2所示，首先输入多标签数据集等待聚类，其中NLN代表非叶子节点，LN代表叶子节点，样本数为N.

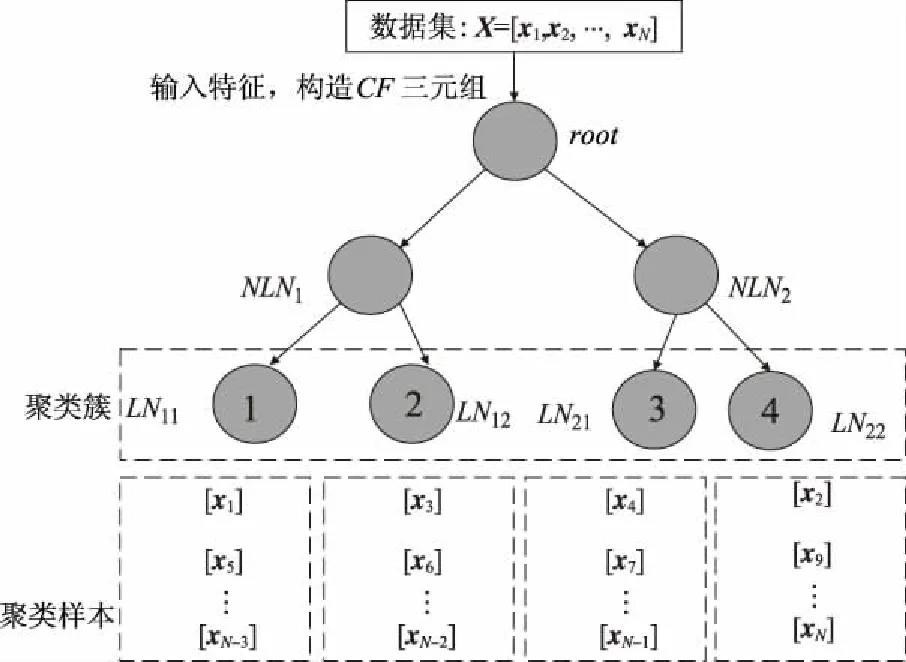
图2 聚类特征树聚类实例

在多标签分类中，数据样本由特征向量和多个标签的输出向量表示.假设相互依赖的标签在输出空间上具有相似的特征，即样本之间存在着一定的关联关系.利用聚类特征树构建出的树形结构，每1个样本的特征最终都会被分配到1个叶子节点上.因此，每个样本都可以获得表示当前叶子节点的编号(如图2中1、2、3、4所示)的聚类簇类别.通过聚类特征过程获取所有样本的聚类簇，添加叶子节点聚类簇Xcluster扩展原始特征空间.最终，得到1个新的训练集D′=(X∪Xcluster,Y)，若样本的特征Xcluster相同，表明样本之前的关系紧密，则认为输出空间有相似的特性.

1.4 标签特定特征

1.4.1随机局部特征转换框架

文中通过构建随机局部特征转换框架来提取标签的特定特征.随机局部特征转换框架的详细过程如图3所示，伪代码见算法2.

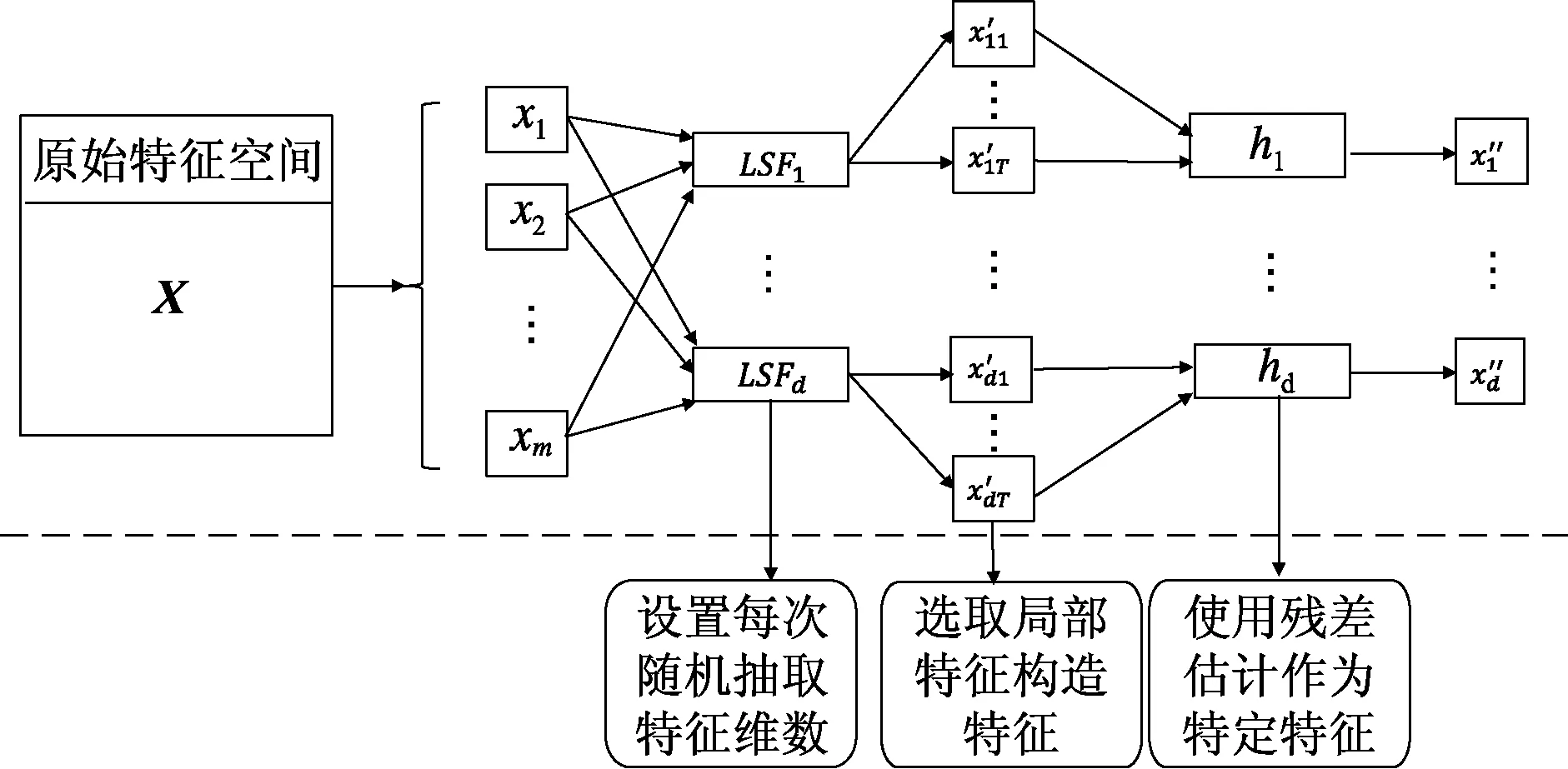
图3 随机局部特征转换框架

算法2随机局部特征转换的标签特定特征学习中定义Trees=GradientBoostingTree(D,X,ratio,T,yi)，其中输入为训练数据D，原始特征集X，随机选择的特征维数比例ratio，树的棵数T，标签yi；输出为Trees.其流程如下：

令Trees=∅

fort=1:Tdo

从原始特征集X中按比例ratio随机选取局部特征子集At；

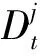
Trees=Trees∪Treet

计算梯度提升树叶子节点的残差预测值

返回Trees

具体而言，输入原始的特征空间到LSF中，对于第j个标签yj，即在图3中的每个LSF中，需要设置树的棵数T值(MLL-BCT算法设置默认T值为100，树的数目即随机选择次数的累积能够保证表达力具有区分度，故通常不应偏小)，以及设置随机局部特征选择维数的占比ratio值(MLL-BCT算法设置默认ratio值为0.3，为保证每次特定地学习少量特征隐藏的信息，故通常不应偏大).合理地设置T值和ratio值可以保障标签特定特征的差异性与细化能力.

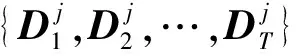
(4)

式中：Xi为第i个训练样本的特征向量；Xi[At]为包含由所选特征索引在Xi的特征向量；yij为第i个训练样本的第j个标签向量.

随机选择局部特征能够保证特定学习少量特征隐藏的信息，随机选择次数的累积保证表达力具有区分度，保障标签特定特征的差异性与细化能力.

1.4.2利用梯度提升树学习残差预测值

在1.4.1节的随机局部特征转换框架中，包含随机抽取T个局部特征子集训练T棵梯度提升树获取叶子节点的残差预测值过程.具体每一棵梯度提升树学习生成负梯度残差见算法3，其中输出的叶子节点残差预测值为对应标签转化的特定特征.

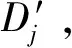
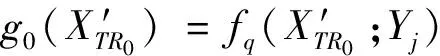
fori←1 totdo

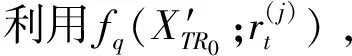
end for

具体针对任意一棵树Treet的特定特征学习过程，也即是为了增加原始特征空间的差异性，文中构建标签特定特征，利用每次迭代的残差来描述局部特征，且作为额外特征来反映特征空间中的局部信息，同时对标签直接建模，增加模型的表达能力，方法如下式(5)-(8)所示：

(5)

(6)

(7)

(8)

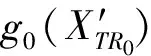
1.4.3学习标签特定特征

学习标签特定特征即是获取所有梯度提升树学习生成负梯度残差的过程，示例如图4所示.

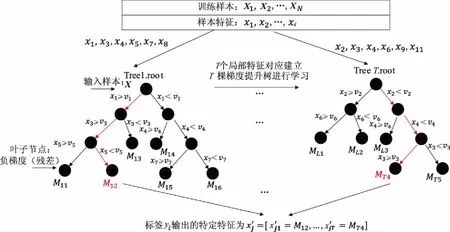
图4 学习标签特定特征的示例

对任意一棵树输出的叶子节点残差预测值为对应标签转化的特定特征.而对于每棵树而言，是基于原始特征空间进行随机选择的特征子集来学习的，树的棵数太少会导致标签特定特征一定的噪声.为了避免每棵树相似性太高，通常T取值不能偏小，同时每棵树学习的特征子集维数采样率ratio不应过大.

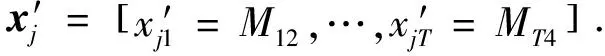
2 试验结果与分析

2.1 数据集与对比方法

为了对算法性能进行全面评估，选择了11个公开的多标签数据集进行试验，所有的数据集均来自于Mulan(网址是http:∥mulan.sourceforge.net/datasets-mlc.html)，数据集来源涵盖了生物、文本、音乐、视频、图像多个领域.同时，样本数量规模选取为数百到数万区间(具体规模为194到43 907)，包含较小样本数目数据集如图像领域的flag，以及较大样本数目数据集如视频领域的mediamill；特征维度的数量级为数十维到数万维，包含较低维数据集如flag、emotions，以及来自文本领域的较高维数据集yahoo(arts1)；所选数据集对应的最小标签数目为6，最大标签数目为374.表1为数据集详细信息，数据集主要特征的差异保障了试验数据的多样性和全面性.

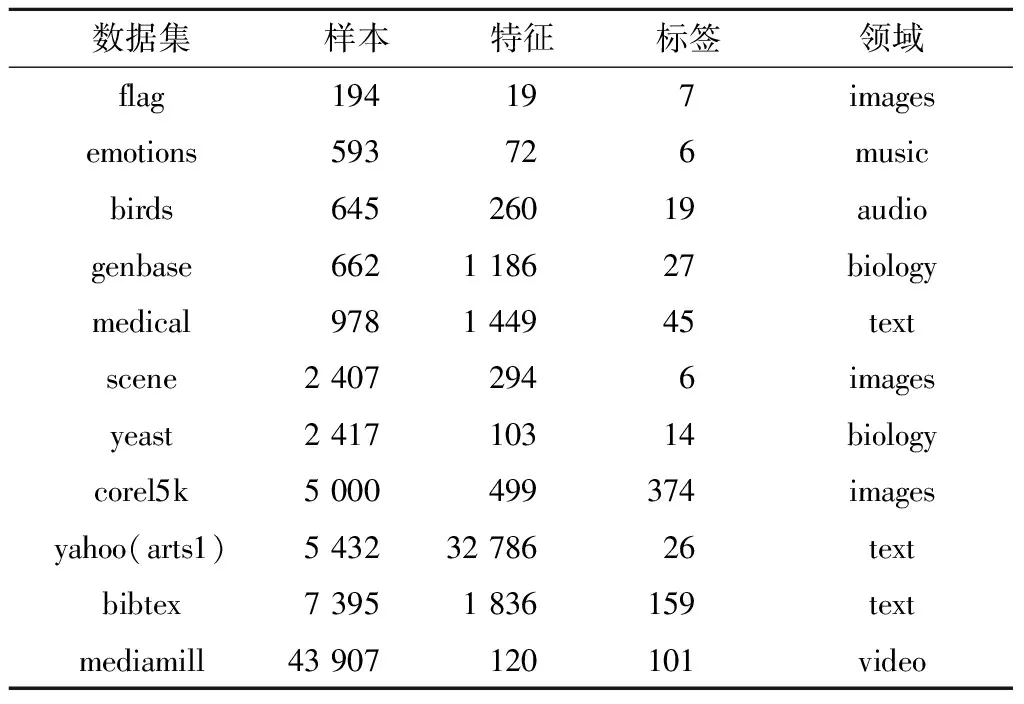
表1 数据集信息表

文献[10]中采用迭代优化变量学习权重的方法相对直接构建特定特征而言模型更加复杂，因此未进行此算法的对比试验.

文中参考并选取了REEL(改进于标签特定特征领域最经典的LIFT算法)一文的对比试验算法包括BR、LIFT、LLSF算法，并额外增加了基于LLSF改进的LLSF-DL算法，同时对比REEL和LF-LPLC算法，共计6个对比算法保证试验的说服力，表2给出了对比算法信息.

表2 对比算法信息表

2.2 模型结果与分析

在多标签分类算法评估与分析试验中，对所有多标签数据集都采用相同的划分方式，用50%的数据进行训练，其余50%进行测试.在计算评价指标时，将各结果取重复10次试验的平均值进行统计，文中选择Xgboost[12]算法作为基分类器.

试验结果表中评价指标后的“↓”表示指标取值越小性能越佳，符号“↑”表示指标取值越大性能越佳，AveRank表示该算法的平均排名.文中主要从MLL-BCT算法分类性能、聚类特征树的有效性、算法关键参数的选取3个方面进行分析.

2.2.1算法分类性能比较

表3-7为5个不同评价指标下各个多标签学习算法在各多标签数据集上的学习性能，从各结果表中的平均排名可以知道MLL-BCT算法排名均为第1.其中Ranking-loss的性能优势稍弱，其余评估指标有着显著的优势.

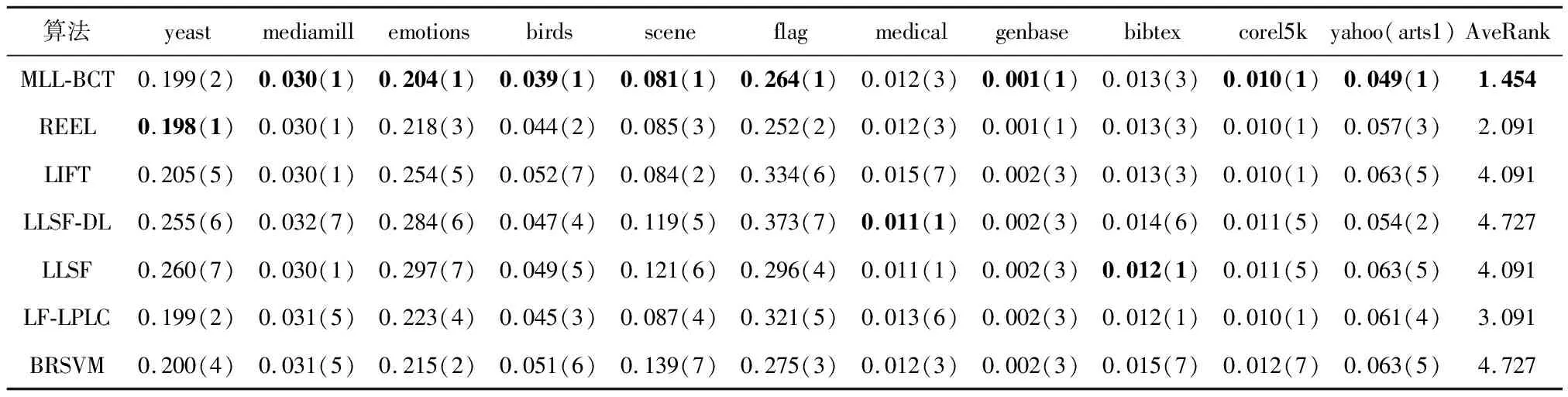
表3 不同算法的Hamming Loss↓试验结果(均值(排序))

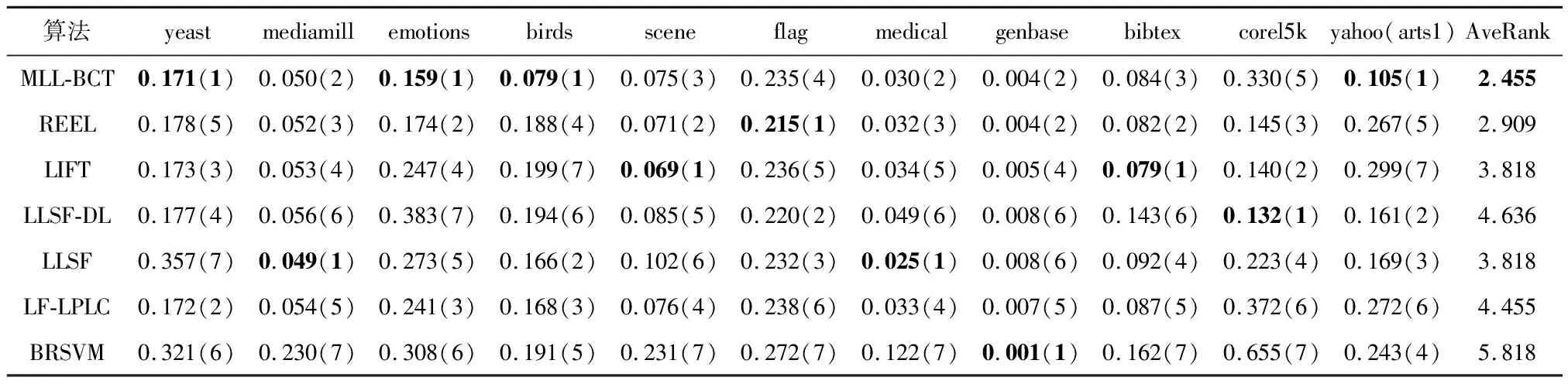
表4 不同算法的Ranking Loss↓试验结果(均值(排序))

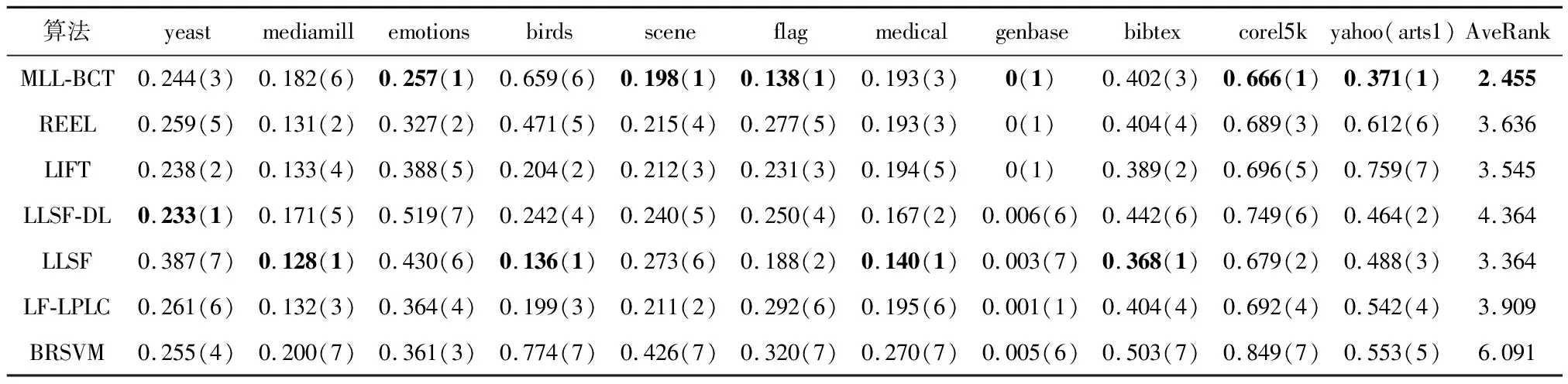
表5 不同算法的One-error↓试验结果(均值(排序))

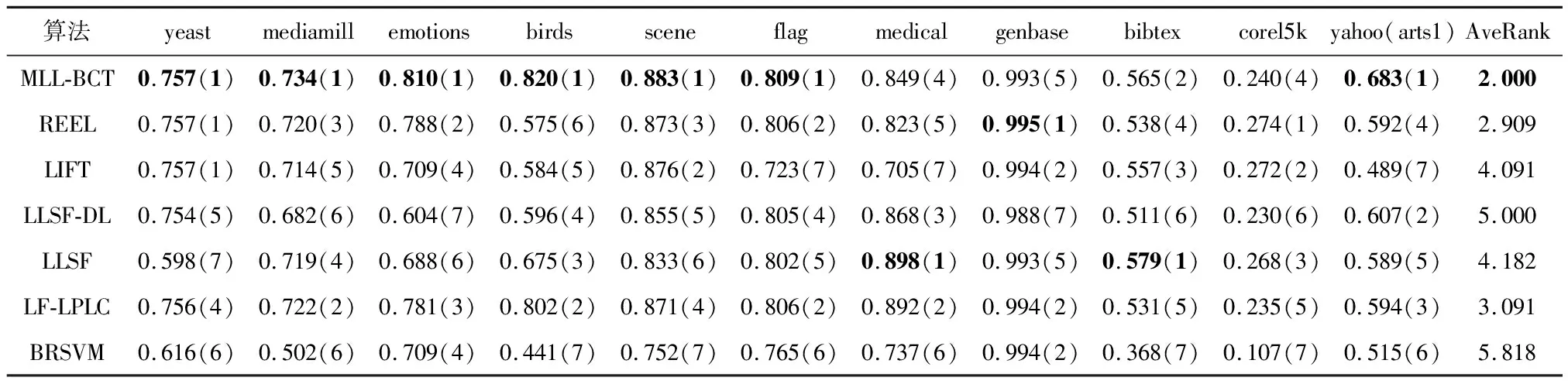
表6 不同算法的Average Precision↑试验结果(均值(排序))

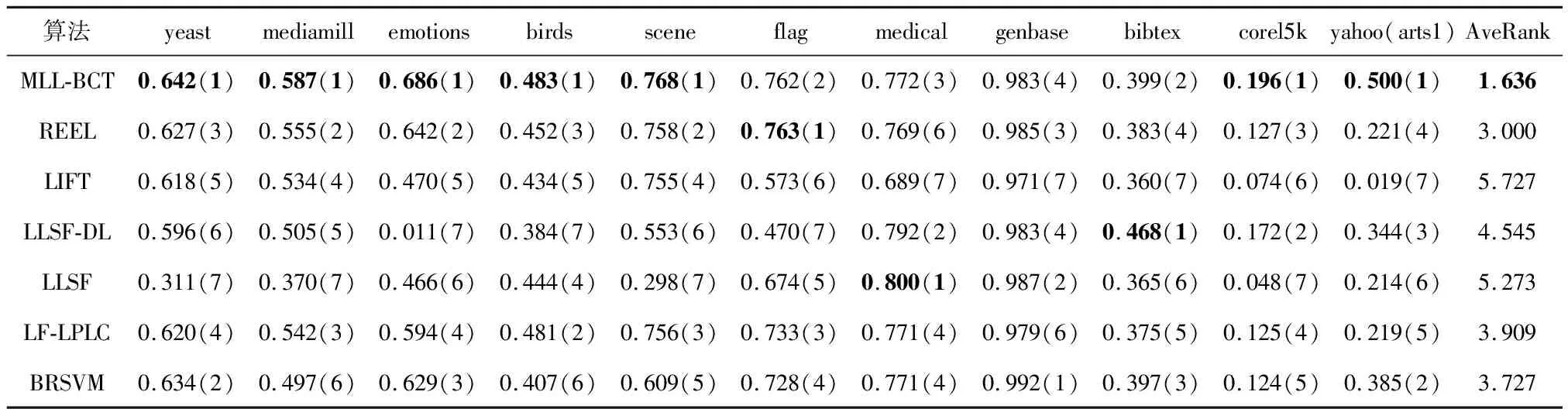
表7 不同算法的Micro-averaged F-Measure↑试验结果(均值(排序))

为了进一步检验各算法之间的性能差异，应用Friedman检验这7种算法有无显著性差异，提出原假设：这7种多标签分类算法是等价的，没有显著性差异.表8给出了5个评价指标的Friedman假设检验结果.

由表8可见，由于p远小于0.05，因此拒绝原假设，证明这7种算法存在显著差异性.

表8 各分类评估指标的Friedman检验结果表

此外，表9进一步给出了算法的相对性能比较，为方便性能得分统计展示，分别设定各算法的得分为A1-A7：MLL-BCT(A1), REEL(A2), LIFT(A3), LLSF-DL(A4), LLSF(A5), LF-LPLC(A6), BR-SVM(A7).

表9 各多标签学习算法的性能得分统计表

在表9中，A1>A2表示在给定的评价指标上，基于显著度0.05的威尔科克森符号秩检验，A1对应算法的性能显著优于A2对应算法.文中通过打分的方式对各学习算法的性能进行总体评价，若A1>A2，则A1的分数加1，A2的分数减1，比较每个算法的最终分数，可以对算法得分进行排序，文中A1(MLL-BCT)最高.由表8和表9证明了文中算法显著优于其余算法.

2.2.2算法聚类特征树有效性的验证

在MLL-BCT中，提出了采用聚类特征树算法来挖掘样本之间的关联关系，为了检验聚类特征树算法的有效性，将聚类特征树这一过程作为控制变量，比较MLL-BCT与替换其他聚类方法(Kmeans、DBSCAN)以及不使用聚类方法，但其余过程都与MLL-BCT保持一致的3种算法性能.

表10-14为5个不同评价指标下算法在各多标签数据集上的学习性能，可以发现在各评估指标上MLL-BCT算法平均排名均为第1，说明MLL-BCT(CF-Tree)优于其余算法，证明了CF-Tree的有效性.

表10 聚类过程不同算法的Hamming Loss↓试验结果(均值(排序))

表11 聚类过程不同算法的Ranking Loss↓试验结果(均值(排序))

表12 聚类过程不同算法的One-error↓试验结果(均值(排序))

表13 聚类过程不同算法的Average Precision↑试验结果(均值(排序))

表14 聚类过程不同算法的Micro-averaged F-Measure↑试验结果(均值(排序))

2.2.3算法关键参数分析

算法MLL-BCT核心在于构建标签特定特征的过程.构建标签特定特征时随机采样特征的采样率ratio和梯度提升树的棵数T是算法的2个关键参数.试验对比数据集较多，因此这里选取了其中4个数据集进行关键参数分析的可视化.

首先研究算法MLL-BCT对参数ratio的敏感度，给定T参数值为100时，对ratio值以0.2为步长，在0.1到0.9内进行试验.图5给出了关键参数ratio的可视化分析结果.

图5 算法MLL-BCT在各指标下的随机采样率参数变化结果图

整体上综合考量多个评价指标的情况下看，由图5可见，在ratio值为0.3时，可以达到最优值.但是部分数据集，如图5c中的emotions，图5e中的birds，随着ratio的增加，性能反而会提升，可能的原因是其样本数过少，或是特征数过少，当模型构建标签特定特征时，需要一定量的特征来表征这个标签，因此随着ratio值变大，分类性能增强.但对于大部分数据集选取局部特征构造特征时，ratio值偏小时能保证特征子集的表达能力不同，从而保障标签特定特征相异性.同理，研究了算法对参数T的敏感度，给定参数ratio值为0.3时，对不同的T值，以20为步长，在范围从40到140内对算法进行试验.

图6给出了算法MLL-BCT在各指标下的梯度提升树棵树参数变化结果.

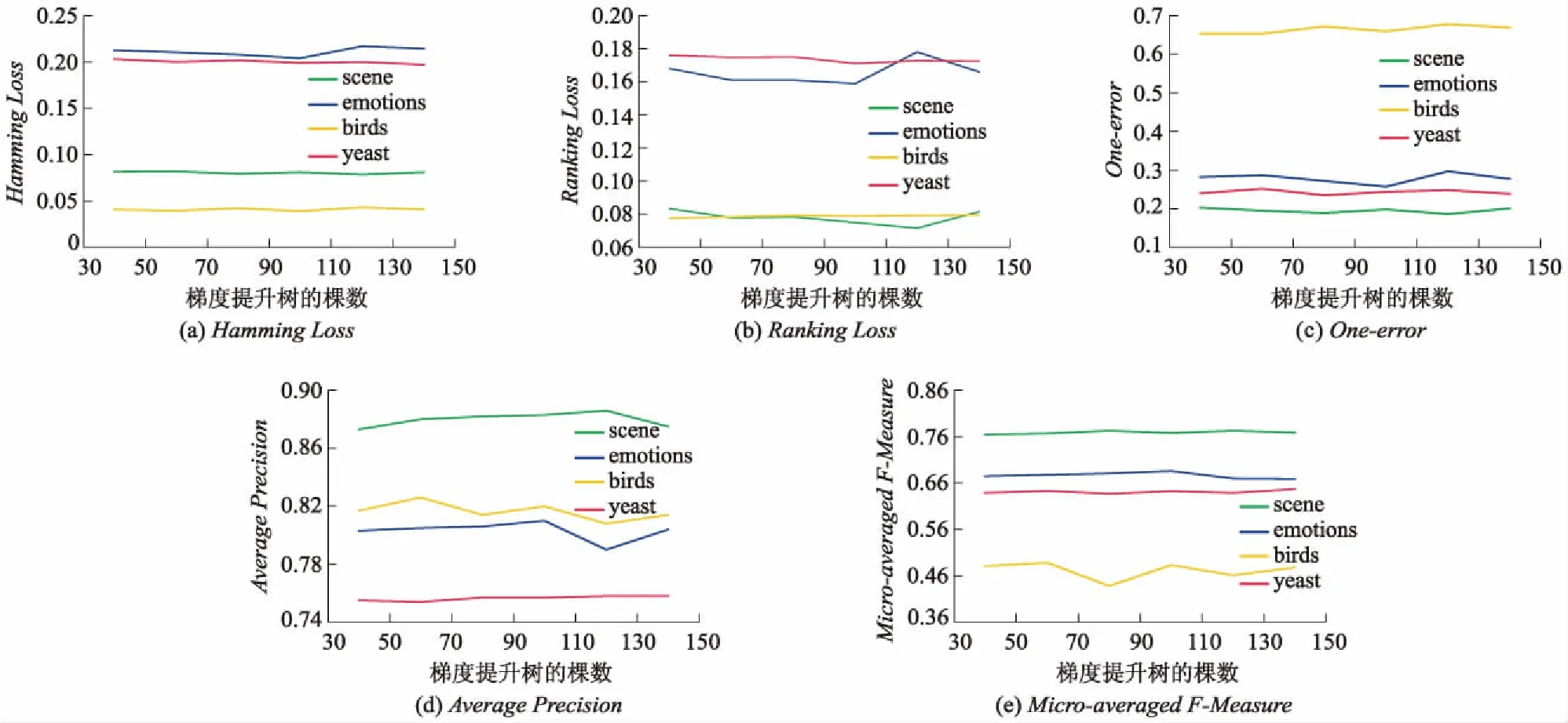
图6 算法MLL-BCT在各指标下的梯度提升树棵树参数变化结果图

由图6可见，算法整体的性能在T值为100时达到最优值.原因在于当ratio值偏小时，用于构建标签特定特征的特征子集维数偏小，则需要足够的梯度提升树结果来挖掘更全面的隐藏信息.存在少部分数据集，如图6a中的scene，图6b中的emotions当T增大时性能逐渐不稳定，甚至会变差，可能的原因是原始特征空间表达能力较好，随着T增加，标签特定特征数也增加，过多的标签特定特征会引起模型过拟合，从而导致预测性能变差.

综合以上的对比分析，文中分别设置MLL-BCT算法ratio值和T值的默认值为0.3和100.

3 结 论

1)利用CF-Tree挖掘可以充分挖掘样本内在关联，寻找输出空间中的相似特征，性能优于其余聚类算法.

2)在随机局部特征转换框架中应用梯度提升树模型致力于利用局部的特征为每个标签构建特定的特征，提升单个标签表达能力，在多标签分类试验结果上各评估指标对比相应领域先进的算法取得了提升.

3)文中方法主要致力于进行特征空间的转化以获取与标签最相关的特征，虽然这些特征有效地提升了分类性能，但引起生成的特征空间维度明显增加，使得特征空间中可能存在着冗余信息，未来还可以基于标签特定特征的降维方法进行研究.